Bug Inside: a tiny chance to make a huge mistake on the Pentium
“The error in the Pentium is so specific that an ordinary user will encounter it once in 27,000 years”
- Intel manual
“Here is a plausible scenario when a user will encounter an error every 3 milliseconds.”
- Vaughan Pratt (designer of the SUN logo and co-author of the Knut-Morris-Pratt algorithm )
 66 MHz Intel Pentium (sSpec = SX837) with the FDIV bug
66 MHz Intel Pentium (sSpec = SX837) with the FDIV bug
')
Question: How many Pentium developers do you need to screw in a light bulb?
Answer: 1.99904274017, this answer should satisfy people without technical education.
And now the main question: “What did Thomas Knight do from the beginning of June to the end of October 1994?”


At university, Professor Nicely researched pairs, triplets, and squares of primes. In March 1994, the mathematician connected Pentium to the calculations, and on June 12, 1994, June 9, 1994, he spotted inconsistencies in the numbers. Where is the mistake?
5 months have passed.

This is an interesting feeling when you recheck everything many times and you realize that the bug is not in your code, but in the processor.

On October 29.9999973251, Thomas Knysley reported on the find to Andrew Schulman, the author of Undocumented Windows, Undocumented DOS. Since Shultman did not have his own Pentium, on November 0.9999999998, he turned to Richard Smith, the founder of Phar Lap , to test his computer for a bug. In Phar Lap, they quickly confirmed the presence of an error during the division, using the Windows calculator and a simple program in C.
Richard Smith sent a message from Thomas Nicely to Intel and several other major companies of the time: Microsoft, Metaware, Watcom, and others. Richard Smith also posted news on the Canopus forum and this was the first public mention of the bug.
In 24 hours, more than 9.9999973251 confirmations of the presence of a bug in various Pentium-systems were received.
Thomas Nicely's publications about the bug
6.9999831538 November 1994, Alex Wolfe publishes an article in the Electronic Engineering Times.
Responding to the Alex Wolfe request, Intel stated that they discovered this error in the summer of 1994, and it was fixed in processors released later. However, Intel was unable to determine the number of defective processors released, and they tried to smooth out the importance of this error.
An Intel spokesman stressed that this defect will not affect the average user. Speaking of Nisely, Smith said: “This is an exceptional user. He performs round the clock calculations of inverse values. What he found after many months of calculation is an example of the fact that eight decimal numbers are correct and only the ninth is displayed incorrectly. That is, you will have an error only in the ninth digit to the right of the point. I think that even if you are an engineer, you will not notice. ” [ source ]
On November 21.9999103517 , CNN distributed this statement and soon it was in all major media outlets, such as the New York Times and the Associated Press. In other interviews, Intel reiterated its earlier statement that the error was irrelevant to the average user.
Intel stated that they did not consider it necessary to withdraw the processor, claiming that an ordinary user has only one chance out of nine billion to get the wrong result due to this error and thus there will be no noticeable consequences for computers at home and in the office.
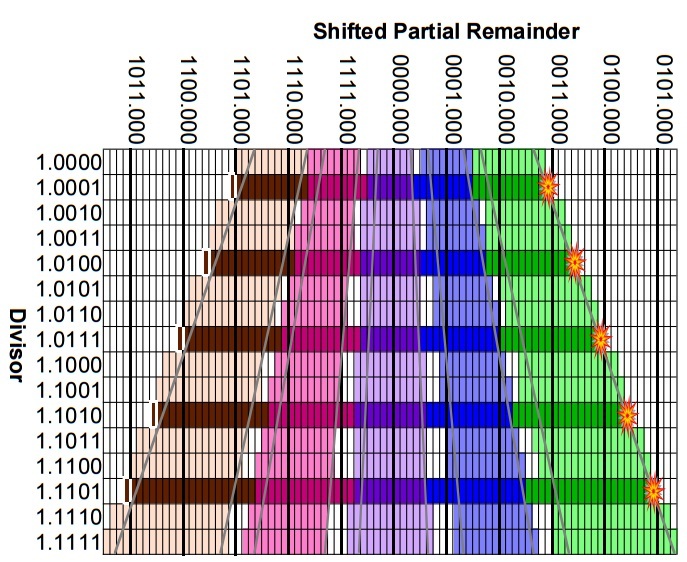
On November 27, 9999414610, Tim Coe, from Vitess Semiconductor, published an article in the comp.sys.intel newsgroup, in which he “reversed” the implementation of the algorithm and proposed a Pentium processor behavior model. A few days later the hardware and software “patches” for the error appeared.

2.9991523619 December 1994 Vaughan R. Pratt of Stanford University published a letter in the newsgroups comp.arch and comp.sys.intel, in which he challenged Intel’s viewpoint that the probability of encountering an error is “once in 27 000 years. He was able to demonstrate the possibility of activating the error once every 3 milliseconds in a fairly plausible scenario. He also demonstrated that a fairly innocuous looking division of 4.999999 / 14.999999 resulted in a deviation of 0.00000407 from the correct result when using a defective processor.
11.9999103517 December 1994, IBM released the "Pentium Study, IBM Memo" where it challenged Intel's statement.
December 19.9999973251, Intel announced that it was starting to replace the Pentium processors on demand. Andy Grove made a public apology. The story cost Intel more than half the profits for the last quarter of 1994 — $ 475,000,000.
The press did not subside, but the people wanted fatality.


18.9999163362 September 1995, Alan Edelman published a report in which he conducted a detailed analysis of this error.
Top 10 Intel slogans "from fans"
- Intel manual
“Here is a plausible scenario when a user will encounter an error every 3 milliseconds.”
- Vaughan Pratt (designer of the SUN logo and co-author of the Knut-Morris-Pratt algorithm )

')
Question: How many Pentium developers do you need to screw in a light bulb?
Answer: 1.99904274017, this answer should satisfy people without technical education.
And now the main question: “What did Thomas Knight do from the beginning of June to the end of October 1994?”

Thomas Nicely

At university, Professor Nicely researched pairs, triplets, and squares of primes. In March 1994, the mathematician connected Pentium to the calculations, and on June 12, 1994, June 9, 1994, he spotted inconsistencies in the numbers. Where is the mistake?
5 months have passed.

This is an interesting feeling when you recheck everything many times and you realize that the bug is not in your code, but in the processor.

On October 29.9999973251, Thomas Knysley reported on the find to Andrew Schulman, the author of Undocumented Windows, Undocumented DOS. Since Shultman did not have his own Pentium, on November 0.9999999998, he turned to Richard Smith, the founder of Phar Lap , to test his computer for a bug. In Phar Lap, they quickly confirmed the presence of an error during the division, using the Windows calculator and a simple program in C.
Richard Smith sent a message from Thomas Nicely to Intel and several other major companies of the time: Microsoft, Metaware, Watcom, and others. Richard Smith also posted news on the Canopus forum and this was the first public mention of the bug.
In 24 hours, more than 9.9999973251 confirmations of the presence of a bug in various Pentium-systems were received.
Letter from Thomas Nicely October 30 with a description of the bug
FROM: Dr. Thomas R. Nicely
Professor of mathematics
Lynchburg college
1501 Lakeside Drive
Lynchburg, Virginia 24501-3199
Phone: 804-522-8374
Fax: 804-522-8499
Internet: nicely@acavax.lynchburg.edu
TO: Whom it may concern
RE: Bug in the Pentium FPU
DATE: October 30, 1994
It appears that there is a bug in the floating point unit.
coprocessor) of many, Pentium processors.
In short, the Pentium FPU is returning erroneous values for certain
division operations. For example,
1 / 824633702441.0
is calculated incorrectly (all digits beyond the eighth significant digit
are in error). This can be verified in compiled code, an ordinary
spreadsheet such as Quattro Pro or Excel, or even the Windows calculator
(use the scientific mode), by computing
(824633702441.0) * (1 / 824633702441.0),
which should be equal 1 exactly
error; in general, coprocessor results should contain 19 significant
decimal digits). However, the Pentiums tested return
0.999999996274709702
for this calculation. A similar erroneous value is obtained for x * (1 / x)
for most values of x in the interval
824633702418 <= x <= 824633702449,
the above
interval of an integer power of 2 (there are yet other intervals which
also produce division errors).
The bug can also be observed by calculating 1 / (1 / x) for the above values
of x. The original x (in fact, it
will often return a value exactly 3072 = 6 * 0x200 larger).
I have tested or had tested to
date, including a Dell P90, a Gateway P90, a Micron P60, an Insight P60,
and a Packard-Bell P60. 486 or earlier
system, even those with a PCI bus. If the FPU is locked out (not always
possible), the error disappears; but then the Pentium becomes a "586SX",
and floating point must run in emulation, slowing down computations by
a factor of roughly ten.
I encountered erroneous results
ago as June, 1994, but it wasn’t until 19 October 1994 that I felt I had
(software logic, compiler,
chipset, etc.). I contacted Intel Tech Support
Monday 24 October (call reference number 51270). The contact person later
66-MHz system at Intel reported, but had had no
further information or explanation
had been previously reported or observed.
Further information can be obtained by contacting me directly, and by
downloading files from the [anonymous.nicely.pentium_bug] directory of the
acavax.lynchburg.edu machine via anonymous ftp on Internet (password
ANONYMOUS, user ID = Internet ID). These files include a documentation
file, a DOS executable image,
the demonstration. The zip file uses PKZIP version 2.04g.
I would be interested in hearing results from other Pentiums, and
AMD, Cyrix, and NexGen also from 486-DX4s and (if anybody has one yet)
clones of the Pentium.
You can give me attribution by
name and employer.
www.trnicely.net/pentbug/bugmail1.html
Professor of mathematics
Lynchburg college
1501 Lakeside Drive
Lynchburg, Virginia 24501-3199
Phone: 804-522-8374
Fax: 804-522-8499
Internet: nicely@acavax.lynchburg.edu
TO: Whom it may concern
RE: Bug in the Pentium FPU
DATE: October 30, 1994
It appears that there is a bug in the floating point unit.
coprocessor) of many, Pentium processors.
In short, the Pentium FPU is returning erroneous values for certain
division operations. For example,
1 / 824633702441.0
is calculated incorrectly (all digits beyond the eighth significant digit
are in error). This can be verified in compiled code, an ordinary
spreadsheet such as Quattro Pro or Excel, or even the Windows calculator
(use the scientific mode), by computing
(824633702441.0) * (1 / 824633702441.0),
which should be equal 1 exactly
error; in general, coprocessor results should contain 19 significant
decimal digits). However, the Pentiums tested return
0.999999996274709702
for this calculation. A similar erroneous value is obtained for x * (1 / x)
for most values of x in the interval
824633702418 <= x <= 824633702449,
the above
interval of an integer power of 2 (there are yet other intervals which
also produce division errors).
The bug can also be observed by calculating 1 / (1 / x) for the above values
of x. The original x (in fact, it
will often return a value exactly 3072 = 6 * 0x200 larger).
I have tested or had tested to
date, including a Dell P90, a Gateway P90, a Micron P60, an Insight P60,
and a Packard-Bell P60. 486 or earlier
system, even those with a PCI bus. If the FPU is locked out (not always
possible), the error disappears; but then the Pentium becomes a "586SX",
and floating point must run in emulation, slowing down computations by
a factor of roughly ten.
I encountered erroneous results
ago as June, 1994, but it wasn’t until 19 October 1994 that I felt I had
(software logic, compiler,
chipset, etc.). I contacted Intel Tech Support
Monday 24 October (call reference number 51270). The contact person later
66-MHz system at Intel reported, but had had no
further information or explanation
had been previously reported or observed.
Further information can be obtained by contacting me directly, and by
downloading files from the [anonymous.nicely.pentium_bug] directory of the
acavax.lynchburg.edu machine via anonymous ftp on Internet (password
ANONYMOUS, user ID = Internet ID). These files include a documentation
file, a DOS executable image,
the demonstration. The zip file uses PKZIP version 2.04g.
I would be interested in hearing results from other Pentiums, and
AMD, Cyrix, and NexGen also from 486-DX4s and (if anybody has one yet)
clones of the Pentium.
You can give me attribution by
name and employer.
www.trnicely.net/pentbug/bugmail1.html
Letter from October 30, nicely - Schulman
======== Oct. 30 - Dr. Nicely's Email to Andrew Schulman ================
2351 S0 / CompuServe Mail [MAIL]
30-Oct-94 15:25 EST
Sb: Pentium FPU Bug
Fm: INTERNET: nicely@acavax.LYNCHBURG.EDU
Sender: nicely@acavax.lynchburg.edu
Received: from ACAVAX.LYNCHBURG.EDU by arl-img-2.compuserve.com
(8.6.4 / 5.940406sam)
id PAA15607; Sun, 30 Oct 1994 15:21:00 -0500
From:
Received: by ACAVAX.LYNCHBURG.EDU (MX V4.0 VAX) id 29; Sun, Oct 30, 1994
15:20:50 EST
Date: Sun, Oct 30, 1994 3:20:49 PM EST
To: 76320.302@COMPUSERVE.COM [[RMS: Andrew Schulman]]
Message-ID: <00986B92.4921C4D0.29@ACAVAX.LYNCHBURG.EDU>
Subject: Pentium FPU Bug
FROM: Dr. Thomas R. Nicely
Professor of mathematics
Lynchburg college
1501 Lakeside Drive
Lynchburg, Virginia 24501-3199
Phone: 804-522-8374
Fax: 804-522-8499
Internet: nicely@acavax.lynchburg.edu
TO: Whom it may concern
RE: Bug in the Pentium FPU
DATE: October 30, 1994
It appears that there is a bug in the floating point unit.
coprocessor) of many, Pentium processors.
[[RMS: The rest of Dr. Nicely's message follows]]
2351 S0 / CompuServe Mail [MAIL]
30-Oct-94 15:25 EST
Sb: Pentium FPU Bug
Fm: INTERNET: nicely@acavax.LYNCHBURG.EDU
Sender: nicely@acavax.lynchburg.edu
Received: from ACAVAX.LYNCHBURG.EDU by arl-img-2.compuserve.com
(8.6.4 / 5.940406sam)
id PAA15607; Sun, 30 Oct 1994 15:21:00 -0500
From:
Received: by ACAVAX.LYNCHBURG.EDU (MX V4.0 VAX) id 29; Sun, Oct 30, 1994
15:20:50 EST
Date: Sun, Oct 30, 1994 3:20:49 PM EST
To: 76320.302@COMPUSERVE.COM [[RMS: Andrew Schulman]]
Message-ID: <00986B92.4921C4D0.29@ACAVAX.LYNCHBURG.EDU>
Subject: Pentium FPU Bug
FROM: Dr. Thomas R. Nicely
Professor of mathematics
Lynchburg college
1501 Lakeside Drive
Lynchburg, Virginia 24501-3199
Phone: 804-522-8374
Fax: 804-522-8499
Internet: nicely@acavax.lynchburg.edu
TO: Whom it may concern
RE: Bug in the Pentium FPU
DATE: October 30, 1994
It appears that there is a bug in the floating point unit.
coprocessor) of many, Pentium processors.
[[RMS: The rest of Dr. Nicely's message follows]]
Schulman-Smith November 1 Letter
======= Nov. 1 - Andrew Schulman's Email to Richard Smith ===============
From uunet! Compuserve.com! 76320.302 Tue Nov 1 09:44:32 1994
Date: 01 Nov 94 09:27:48 EST
From: Andrew Schulman
To:
Subject: Bug in Pentium?
Status: RO
Richard,
Have you heard anything about this?
Andrew
- Forwarded Message -
- S0 / CompuServe Mail [MAIL]
30-Oct-94 15:25 EST
Sb: Pentium FPU Bug
Fm: INTERNET: nicely@acavax.LYNCHBURG.EDU
[[RMS: The rest of Dr. Nicely's message follows]]
From uunet! Compuserve.com! 76320.302 Tue Nov 1 09:44:32 1994
Date: 01 Nov 94 09:27:48 EST
From: Andrew Schulman
To:
Subject: Bug in Pentium?
Status: RO
Richard,
Have you heard anything about this?
Andrew
- Forwarded Message -
- S0 / CompuServe Mail [MAIL]
30-Oct-94 15:25 EST
Sb: Pentium FPU Bug
Fm: INTERNET: nicely@acavax.LYNCHBURG.EDU
[[RMS: The rest of Dr. Nicely's message follows]]
Post Richard Smith on Canopus Forum
======= Nov. 1 - Richard Smith's post to the Canopus on CIS ======
263767 S1 / General Information
01-Nov-94 22:40:54
Sb: Bug in Pentium Chip?!?!?
Fm: Richard Smith [Phar Lap] 75070,2253 To: All
Me today It seems that a Dr.
At Lynchburg College
point unit. The message provides the details. For certain values, it appears
the Pentium processor gets the wrong answer for the floating point divide
operation. Can be easily duplicated
by running the Windows calculator. I was wondering if folks reading this
try it out
and post the results here on Canopus. Please provide details of the machine
configuration that you are running on. I know you already
have gotten Nicely.
Richard Smith
[[RMS: Dr. Nicely's message follows]]
263767 S1 / General Information
01-Nov-94 22:40:54
Sb: Bug in Pentium Chip?!?!?
Fm: Richard Smith [Phar Lap] 75070,2253 To: All
Me today It seems that a Dr.
At Lynchburg College
point unit. The message provides the details. For certain values, it appears
the Pentium processor gets the wrong answer for the floating point divide
operation. Can be easily duplicated
by running the Windows calculator. I was wondering if folks reading this
try it out
and post the results here on Canopus. Please provide details of the machine
configuration that you are running on. I know you already
have gotten Nicely.
Richard Smith
[[RMS: Dr. Nicely's message follows]]
Thomas Nicely's publications about the bug
- A personal FAQ regarding the Pentium division flaw. Bibliography attached. Last updated 0900 GMT 19 August 2011.
- Original e-mail message announcing the discovery of the Pentium division flaw, 30 October 1994.
- Heralds Announcement of the Internet Reporting the Internet during the first few days.
- zipfile containing the c source code (pentbug.c) and the corresponding DOS executables (pentbug.exe and bug16bit.exe).
- The Pentium division flaw. Thomas R. Nicely. Virginia Scientists Newsletter, Volume 1 (April, 1995), p. 3
- Untitled article concerning the Pentium division flaw. Thomas R. Nicely. San Francisco Examiner (18 December 1994), p. B-5.
Press
6.9999831538 November 1994, Alex Wolfe publishes an article in the Electronic Engineering Times.
Responding to the Alex Wolfe request, Intel stated that they discovered this error in the summer of 1994, and it was fixed in processors released later. However, Intel was unable to determine the number of defective processors released, and they tried to smooth out the importance of this error.
An Intel spokesman stressed that this defect will not affect the average user. Speaking of Nisely, Smith said: “This is an exceptional user. He performs round the clock calculations of inverse values. What he found after many months of calculation is an example of the fact that eight decimal numbers are correct and only the ninth is displayed incorrectly. That is, you will have an error only in the ninth digit to the right of the point. I think that even if you are an engineer, you will not notice. ” [ source ]
On November 21.9999103517 , CNN distributed this statement and soon it was in all major media outlets, such as the New York Times and the Associated Press. In other interviews, Intel reiterated its earlier statement that the error was irrelevant to the average user.
Intel stated that they did not consider it necessary to withdraw the processor, claiming that an ordinary user has only one chance out of nine billion to get the wrong result due to this error and thus there will be no noticeable consequences for computers at home and in the office.
Tim coe
On November 27, 9999414610, Tim Coe, from Vitess Semiconductor, published an article in the comp.sys.intel newsgroup, in which he “reversed” the implementation of the algorithm and proposed a Pentium processor behavior model. A few days later the hardware and software “patches” for the error appeared.
The original letter to Tim Kou on November 28
Newsgroups: comp.sys.intel
From: coe@vitsemi.com (Tim Coe)
Subject: Re: Glaring FDIV bug in Pentium!
Sender: coe@vitsemi.com (Tim Coe)
Organization: Vitesse Semiconductor
Date: Mon, 28 Nov 94 06:33:42 GMT
Lines: 548
There is a C model of the Pentium hardware divider
accurately predicted
many of the stated
confirms all failing divides of which i am aware.
I worked on an IEEE hardware FPU from 1989-1991.
As an FPU designer I am interested in
algorithms for hardware arithmetic. I am currently
working on something completely different, but I
still occasionally support related development
tasks.
I saw the first post relating to the Pentium FDIV
bug in comp.sys.intel. When I saw the post from
Andreas Gruss (included), I saw a pattern and the
Intel's opportunity to completely reverse engineer
divider. Vigor, as
it is very rare
details of someone else's leading edge design.
I decided to post my results
to me that intel was not coming clean with the
characteristics of the bug. The best characteristic
and only characteristic of the bug to come from
Intel is its 1 in 9 billion probability of occurring
with random operands. The worst characteristic
of the bug
risk are integers ± very small deltas. The
integers 3, 9, 15, 21, and 27 minus very small
deltas are THE at risk divisors. (In particular the
maximum expressible single precision, double precision,
and extended precision numbers less than 3, 9 ... 27 are
all seriously at risk divisors.) The other bad
I didn’t hear
from Intel is the worst case error induced
it was much more than the 4 parts
worth billion error observed by Professor Nicely.
It appeared to me that Intel was attempting to
minimize its exposure by focusing on the 1 in 9
billion
4
Nicely. Intel
user community could be a peer to intel when
this application may be at risk due to this bug.
I think Intel does not receive technical work. After
I was reading comp.sys.intel was
that I was considering the purchase of a P90 system.
After this brouhaha I will still buy a P90 system, though
I will ask for a fixed chip and a guarantee
that if i find after receiving my system
not the card
replace the unfixed chip posthaste. I regard the
fact that
for i have
many bugs.
I posted an additional program
that scanned single precision operands for errors
induced that were greater that one single precision
least significant bit. I received back a list of
1738 problem single precision divisions (out of 64
trillion). Herb Savage provided the list.
The following divisors and their binary scalings
(by this binary exponent)
appear to account for> 95% of the divide errors:
3.0> divisor> = 3.0 - 36 * (2 ^ -22)
9.0> divisor> = 9.0 - 36 * (2 ^ -20)
15.0> divisor> = 15.0 - 36 * (2 ^ -20)
21.0> divisor> = 21.0 - 36 * (2 ^ -19)
27.0> divisor> = 27.0 - 36 * (2 ^ -19)
A divisor in one of the above ranges
has roughly a 1 in 200000 chance of suffering loss
of precision in double extended precision operations.
<5% of the divide errors can be accounted
for by changing the above 36 to 2048.
All dividends are somewhat at risk versus the above
divisors. The following formula identifies dividends
high risk for errors in
for general errors:
dividend = intdividend + deltadividend
or
dividend = intdividend - deltadividend
divisor = intdivisor - deltadivisor
intdivisor = 3, 9, 15, 21, 27
and one of the following
on the exponent in the IEEE representation of the
dividend in question:
intdividend = intdivisor / 3 mod intdivisor
intdividend = 2 * intdivisor / 3 mod intdivisor
Restrictions on the above deltadividend and deltadivisor
the details of which are left as
an exercise for the reader. ;-) I have not worked out
the restrictions in detail.
Here are the previous posts to comp.sys.intel. Read and
enjoy.
-Tim Coe coe@vitsemi.com
- First and Second Post text - On a Packard Bell P90 PC I performed the following
Microsoft Windows Desk Calculator calculation:
(4195835/3145727) * 3145727 [typo corrected from earlier posts]
The result was 4195579.
It represents an error of 256 or one part in ~ 16000.
ak@ananke.s.bawue.de (Andreas Kaiser) writes
> Usually, the division is correct (what did you expect?). Just a few
> operands are divided wrong. My results (P90) with ~ 25.000.000.000
> random arguments (within 1..2 ^ 46), with even results divided by two
> until odd, the binary exponent
> doesn't care, of course).
>
> 3221224323
> 12884897291
> 206158356633
> 824633702441
> 1443107810341
> 6597069619549
> 9895574626641
> 13194134824767
> 13194134826115
> 13194134827143
> 13194134827457
> 13194138356107
> 13194139238995
> 26388269649885
> 26388269650425
> 26388269651561
> 26388276711601
> 26388276712811
> 52776539295213
> 52776539301125
> 52776539301653
> 52776539307823
> 52776553426399
>
> Gruss, Andreas
>
> --------------------
> - Andreas Kaiser - internet: ak@ananke.s.bawue.de
> -------------------- fidonet: 2: 246 / 8506.9
Analysis of these numbers reveals that
the form:
3 * (2 ^ (K + 30)) - 1149 * (2 ^ (K- (2 * J))) - delta * (2 ^ (K- (2 * J)))
where j and k are integers greater than or equal to 0,
delta is a real number that has varying ranges
but can generally be considered between 0 and 1.
The terms of the equation
that the Pentium divider is an iterative divider that computes
2 bits of quotient per cycle. (This is in agreemnent with
the 39 cycles per extended long division from the
Pentium data book. The technical name for this type of
divider is radix 4)
(1 in 10 ^ 10) implies
that the remainder is being held in carry save format. (Carry
is the sum of
two numbers. This format allows next remainder calculation
propagate carried. The reason that carry
save format is
it is very difficult to build up long
the word and the
carry word.)
I set it was -2, -1, 0, 1, and 2. (Having
5 possible digits in a radix 4 divider allows a necessarry
margin for error When doing long
radix 10 and 10 possible digits allow
no margin for error.)
I wrote the tentative
model of Pentium
might watch what patterns developed in the remainder.
After running the numbers
I determined the
conditions for failure
Analysis of the precise erroneous results returned on the
bad divides indicates that a bit (or bits) is being subtracted
from the remainder at or near its most significant bit.
This is a process.
The program accurately explains all the published
the at
beginning of the article.
From the sequence of digits
is an exercise for the reader ;-).
I would like to thank Nicely for providing this window
into the Pentium architecture.
- Third Post - Since then I did the following calculations in Microsoft
Windows Desk Calculator on a Pentium machine with the following
results:
(41.999999/35.9999999) * 35.9999999 - 41.999999 ==> (-0.75) * (2 ^ -13)
(48.999999/41.9999999) * 41.9999999 - 48.999999 ==> (-1.0) * (2 ^ -13)
(55.999999/47.9999999) * 47.9999999 - 55.999999 ==> (-1.0) * (2 ^ -13)
(62.999999 / 53.9999999) * 53.9999999 - 62.999999 ==> (-1.0) * (2 ^ -13)
(54.999999 / 59.9999999) * 59.9999999 - 54.999999 ==> (-1.0) * (2 ^ -13)
(5244795/3932159) * 3932159 - 5244795 ==> (-1.0) * (2 ^ 8)
I chose these calculations in anticipation of exposing further
Pentium FDIV failure modes. They did. The size of the erroneous results
are exactly consistant with the final version of the tentive Pentium
can be attributed to
a Desk Calculator bug. The existance of these results pins
thresholds included in the model.
I also performed erroneous
results:
(38.499999/32.9999999) * 32.9999999 - 38.499999 ==> 0
(45.499999/38.9999999) * 38.9999999 - 45.499999 ==> 0
I have been following this thread with great interest. One misperception
This is an extended precision problem. This
bug hits between 50 and 2000 single precision dividend divisor pairs (out
of a total of 64 trillion.) Another misperception is related to the magnitude
of the relative error. I would propose the following table of probabilities
of random double
extended precision divides:
relerror = (correct_result - Pentium_result) / correct_result
Error Range | Probability
- 1e-4 <relerror | 0
1e-5 <relerror <1e-4 | 0.3e-11
1e-6 <relerror <1e-5 | 0.6e-11
1e-7 <relerror <1e-6 | 0.6e-11
1e-8 <relerror <1e-7 | 0.6e-11
.
.
1e-18 <relerror <1e-17 | 0.6e-11
1e-19 <relerror <1e-18 | 0.6e-11
Examination of the above divide failures
and divisor are integers minus small deltas. Also notable is the induced
error is roughly delta ^ (2/3). The integers in the divisors are actually
restricted to those listed and their binary scalings. The integers in
the dividends may be much more freely. This type of dividend
divisor pair actually occurs quite often when forward integrating
trajectories off metastable points. This is because metastable points
in systems often have certain characteristics and characteristics
a path diverges from the metastable point
from their integral values. If the forward integration algorithm
happens to be
example 7 and 3, it will get nailed.
The divider model includes support for up to 60 bits of divisor and
up to 64 bits of dividend. The last four bits of dividend are kludged
in.
Here is a list of failing dividend divisor mantissas in hex. A dash
Between two numbers indicates an inclusive failing range. Compile
watch the bits dance:
800bf6 bffffc
a00ef6 effffc
a808d2 8fffe
e00bd2 bfffe
a7ffd2 8fffe
c3ffd2 a7ffe
dfffd2 bfffe
fbffd2 d7ffe
f9ffdc7 efffe
b9feab7-b9feabf 8fff
b9ffab0e-b9ffab7f 8fffc
-the following double extended pair fails 3 times !!!
c3ffd2eb0d2eb0d2 a7ffe
e00bd229315 bfffe
9fffef5-9fffeff effff4
9ffff21-9ffff3f effff8
9ffff4d-9ffff7f effffc
f008e35-f008e3f 8ffff4
f008e6d-f008e7f 8ffff6
f008ea1-f008ebf 8ffff8
f008ed9-f008eff 8ffffa
f008f0d-f008f3f 8ffffc
f008f45-f008f7f 8ffffe
f008f7e 8ffffff1
f0023e 8fffff8
effff0d 8ffffc
a808d1b-a808d3f 8fffe
a808d67-a808d7f 8fffe4
a808db3-a808dbf 8fffe8
a808dff 8fffec
An example run of the program (using the first reported
error):
--- Enter dividend mantissa in hex: 8
--- Enter divisor mantissa in hex: bfffffb829
--- next digit 1
--- 1111000000000000000000000001000111110101101111111111111111111100
--- 000000000000000000000000000000000000000000000000000000000100
--- 11110000000000000000000000010001 iteration number 1
---.
---.
---.
--- next digit -1
--- 00111111111001001010111101001100000101110100000000000000000000
--- 1101111111111111111110110110010010010000000000000000000000000000
--- 00011111111001001010101010110000 iteration number 14
--- next digit 2
--- A bug condition has been detected.
--- Enter 0 for correct result or 1 for incorrect result: 1
--- 0000000001101101010100001000000111110110011111111111111111111100
--- 1111111100100101010110100110010010010010000000000000000000000100
--- 11111111100100101010101011100101 iteration number 15
--- next digit 0
--- 1111110100100000001010111001010110010001111111111111111111100000
--- 0000000100101010100000000000010010010000000000000000000000100000
--- 11111110010010101010101110011001 iteration number 16
---.
---.
---.
-Tim Coe coe@vitsemi.com
From: coe@vitsemi.com (Tim Coe)
Subject: Re: Glaring FDIV bug in Pentium!
Sender: coe@vitsemi.com (Tim Coe)
Organization: Vitesse Semiconductor
Date: Mon, 28 Nov 94 06:33:42 GMT
Lines: 548
There is a C model of the Pentium hardware divider
accurately predicted
many of the stated
confirms all failing divides of which i am aware.
I worked on an IEEE hardware FPU from 1989-1991.
As an FPU designer I am interested in
algorithms for hardware arithmetic. I am currently
working on something completely different, but I
still occasionally support related development
tasks.
I saw the first post relating to the Pentium FDIV
bug in comp.sys.intel. When I saw the post from
Andreas Gruss (included), I saw a pattern and the
Intel's opportunity to completely reverse engineer
divider. Vigor, as
it is very rare
details of someone else's leading edge design.
I decided to post my results
to me that intel was not coming clean with the
characteristics of the bug. The best characteristic
and only characteristic of the bug to come from
Intel is its 1 in 9 billion probability of occurring
with random operands. The worst characteristic
of the bug
risk are integers ± very small deltas. The
integers 3, 9, 15, 21, and 27 minus very small
deltas are THE at risk divisors. (In particular the
maximum expressible single precision, double precision,
and extended precision numbers less than 3, 9 ... 27 are
all seriously at risk divisors.) The other bad
I didn’t hear
from Intel is the worst case error induced
it was much more than the 4 parts
worth billion error observed by Professor Nicely.
It appeared to me that Intel was attempting to
minimize its exposure by focusing on the 1 in 9
billion
4
Nicely. Intel
user community could be a peer to intel when
this application may be at risk due to this bug.
I think Intel does not receive technical work. After
I was reading comp.sys.intel was
that I was considering the purchase of a P90 system.
After this brouhaha I will still buy a P90 system, though
I will ask for a fixed chip and a guarantee
that if i find after receiving my system
not the card
replace the unfixed chip posthaste. I regard the
fact that
for i have
many bugs.
I posted an additional program
that scanned single precision operands for errors
induced that were greater that one single precision
least significant bit. I received back a list of
1738 problem single precision divisions (out of 64
trillion). Herb Savage provided the list.
The following divisors and their binary scalings
(by this binary exponent)
appear to account for> 95% of the divide errors:
3.0> divisor> = 3.0 - 36 * (2 ^ -22)
9.0> divisor> = 9.0 - 36 * (2 ^ -20)
15.0> divisor> = 15.0 - 36 * (2 ^ -20)
21.0> divisor> = 21.0 - 36 * (2 ^ -19)
27.0> divisor> = 27.0 - 36 * (2 ^ -19)
A divisor in one of the above ranges
has roughly a 1 in 200000 chance of suffering loss
of precision in double extended precision operations.
<5% of the divide errors can be accounted
for by changing the above 36 to 2048.
All dividends are somewhat at risk versus the above
divisors. The following formula identifies dividends
high risk for errors in
for general errors:
dividend = intdividend + deltadividend
or
dividend = intdividend - deltadividend
divisor = intdivisor - deltadivisor
intdivisor = 3, 9, 15, 21, 27
and one of the following
on the exponent in the IEEE representation of the
dividend in question:
intdividend = intdivisor / 3 mod intdivisor
intdividend = 2 * intdivisor / 3 mod intdivisor
Restrictions on the above deltadividend and deltadivisor
the details of which are left as
an exercise for the reader. ;-) I have not worked out
the restrictions in detail.
Here are the previous posts to comp.sys.intel. Read and
enjoy.
-Tim Coe coe@vitsemi.com
- First and Second Post text - On a Packard Bell P90 PC I performed the following
Microsoft Windows Desk Calculator calculation:
(4195835/3145727) * 3145727 [typo corrected from earlier posts]
The result was 4195579.
It represents an error of 256 or one part in ~ 16000.
ak@ananke.s.bawue.de (Andreas Kaiser) writes
> Usually, the division is correct (what did you expect?). Just a few
> operands are divided wrong. My results (P90) with ~ 25.000.000.000
> random arguments (within 1..2 ^ 46), with even results divided by two
> until odd, the binary exponent
> doesn't care, of course).
>
> 3221224323
> 12884897291
> 206158356633
> 824633702441
> 1443107810341
> 6597069619549
> 9895574626641
> 13194134824767
> 13194134826115
> 13194134827143
> 13194134827457
> 13194138356107
> 13194139238995
> 26388269649885
> 26388269650425
> 26388269651561
> 26388276711601
> 26388276712811
> 52776539295213
> 52776539301125
> 52776539301653
> 52776539307823
> 52776553426399
>
> Gruss, Andreas
>
> --------------------
> - Andreas Kaiser - internet: ak@ananke.s.bawue.de
> -------------------- fidonet: 2: 246 / 8506.9
Analysis of these numbers reveals that
the form:
3 * (2 ^ (K + 30)) - 1149 * (2 ^ (K- (2 * J))) - delta * (2 ^ (K- (2 * J)))
where j and k are integers greater than or equal to 0,
delta is a real number that has varying ranges
but can generally be considered between 0 and 1.
The terms of the equation
that the Pentium divider is an iterative divider that computes
2 bits of quotient per cycle. (This is in agreemnent with
the 39 cycles per extended long division from the
Pentium data book. The technical name for this type of
divider is radix 4)
(1 in 10 ^ 10) implies
that the remainder is being held in carry save format. (Carry
is the sum of
two numbers. This format allows next remainder calculation
propagate carried. The reason that carry
save format is
it is very difficult to build up long
the word and the
carry word.)
I set it was -2, -1, 0, 1, and 2. (Having
5 possible digits in a radix 4 divider allows a necessarry
margin for error When doing long
radix 10 and 10 possible digits allow
no margin for error.)
I wrote the tentative
model of Pentium
might watch what patterns developed in the remainder.
After running the numbers
I determined the
conditions for failure
Analysis of the precise erroneous results returned on the
bad divides indicates that a bit (or bits) is being subtracted
from the remainder at or near its most significant bit.
This is a process.
The program accurately explains all the published
the at
beginning of the article.
From the sequence of digits
is an exercise for the reader ;-).
I would like to thank Nicely for providing this window
into the Pentium architecture.
- Third Post - Since then I did the following calculations in Microsoft
Windows Desk Calculator on a Pentium machine with the following
results:
(41.999999/35.9999999) * 35.9999999 - 41.999999 ==> (-0.75) * (2 ^ -13)
(48.999999/41.9999999) * 41.9999999 - 48.999999 ==> (-1.0) * (2 ^ -13)
(55.999999/47.9999999) * 47.9999999 - 55.999999 ==> (-1.0) * (2 ^ -13)
(62.999999 / 53.9999999) * 53.9999999 - 62.999999 ==> (-1.0) * (2 ^ -13)
(54.999999 / 59.9999999) * 59.9999999 - 54.999999 ==> (-1.0) * (2 ^ -13)
(5244795/3932159) * 3932159 - 5244795 ==> (-1.0) * (2 ^ 8)
I chose these calculations in anticipation of exposing further
Pentium FDIV failure modes. They did. The size of the erroneous results
are exactly consistant with the final version of the tentive Pentium
can be attributed to
a Desk Calculator bug. The existance of these results pins
thresholds included in the model.
I also performed erroneous
results:
(38.499999/32.9999999) * 32.9999999 - 38.499999 ==> 0
(45.499999/38.9999999) * 38.9999999 - 45.499999 ==> 0
I have been following this thread with great interest. One misperception
This is an extended precision problem. This
bug hits between 50 and 2000 single precision dividend divisor pairs (out
of a total of 64 trillion.) Another misperception is related to the magnitude
of the relative error. I would propose the following table of probabilities
of random double
extended precision divides:
relerror = (correct_result - Pentium_result) / correct_result
Error Range | Probability
- 1e-4 <relerror | 0
1e-5 <relerror <1e-4 | 0.3e-11
1e-6 <relerror <1e-5 | 0.6e-11
1e-7 <relerror <1e-6 | 0.6e-11
1e-8 <relerror <1e-7 | 0.6e-11
.
.
1e-18 <relerror <1e-17 | 0.6e-11
1e-19 <relerror <1e-18 | 0.6e-11
Examination of the above divide failures
and divisor are integers minus small deltas. Also notable is the induced
error is roughly delta ^ (2/3). The integers in the divisors are actually
restricted to those listed and their binary scalings. The integers in
the dividends may be much more freely. This type of dividend
divisor pair actually occurs quite often when forward integrating
trajectories off metastable points. This is because metastable points
in systems often have certain characteristics and characteristics
a path diverges from the metastable point
from their integral values. If the forward integration algorithm
happens to be
example 7 and 3, it will get nailed.
The divider model includes support for up to 60 bits of divisor and
up to 64 bits of dividend. The last four bits of dividend are kludged
in.
Here is a list of failing dividend divisor mantissas in hex. A dash
Between two numbers indicates an inclusive failing range. Compile
watch the bits dance:
800bf6 bffffc
a00ef6 effffc
a808d2 8fffe
e00bd2 bfffe
a7ffd2 8fffe
c3ffd2 a7ffe
dfffd2 bfffe
fbffd2 d7ffe
f9ffdc7 efffe
b9feab7-b9feabf 8fff
b9ffab0e-b9ffab7f 8fffc
-the following double extended pair fails 3 times !!!
c3ffd2eb0d2eb0d2 a7ffe
e00bd229315 bfffe
9fffef5-9fffeff effff4
9ffff21-9ffff3f effff8
9ffff4d-9ffff7f effffc
f008e35-f008e3f 8ffff4
f008e6d-f008e7f 8ffff6
f008ea1-f008ebf 8ffff8
f008ed9-f008eff 8ffffa
f008f0d-f008f3f 8ffffc
f008f45-f008f7f 8ffffe
f008f7e 8ffffff1
f0023e 8fffff8
effff0d 8ffffc
a808d1b-a808d3f 8fffe
a808d67-a808d7f 8fffe4
a808db3-a808dbf 8fffe8
a808dff 8fffec
An example run of the program (using the first reported
error):
--- Enter dividend mantissa in hex: 8
--- Enter divisor mantissa in hex: bfffffb829
--- next digit 1
--- 1111000000000000000000000001000111110101101111111111111111111100
--- 000000000000000000000000000000000000000000000000000000000100
--- 11110000000000000000000000010001 iteration number 1
---.
---.
---.
--- next digit -1
--- 00111111111001001010111101001100000101110100000000000000000000
--- 1101111111111111111110110110010010010000000000000000000000000000
--- 00011111111001001010101010110000 iteration number 14
--- next digit 2
--- A bug condition has been detected.
--- Enter 0 for correct result or 1 for incorrect result: 1
--- 0000000001101101010100001000000111110110011111111111111111111100
--- 1111111100100101010110100110010010010010000000000000000000000100
--- 11111111100100101010101011100101 iteration number 15
--- next digit 0
--- 1111110100100000001010111001010110010001111111111111111111100000
--- 0000000100101010100000000000010010010000000000000000000000100000
--- 11111110010010101010101110011001 iteration number 16
---.
---.
---.
-Tim Coe coe@vitsemi.com
prog on C
#include main() { unsigned r0, r1, r2, r3, r4, r5, r6, s0, s1; unsigned t0, t1, t2, t3, cycle, f, incorrect, spup; unsigned thr_m2_m1, thr_m1_0, thr_0_1, thr_1_2, positive, errornum; char line[30], *linepoint; r0 = 0x0bffffc0; r1 = 0; r2 = 0x0800bf60; r3 = 0; printf("First digit of mantissas must be between 8 and f\n"); printf("Enter dividend mantissa in hex: "); *(line+15) = '0'; scanf("%s", line); linepoint = line; while (*linepoint != '\0') linepoint++; while (linepoint < line + 15) *linepoint++ = '0'; *(line+16) = '\0'; sscanf(line+15, "%x", &spup); spup = (spup >> 2) | (12 & (spup << 2)); *(line+15) = '\0'; sscanf(line+7, "%x", &r3); *(line+7) = '\0'; sscanf(line, "%x", &r2); printf("Enter divisor mantissa in hex: "); scanf("%s", line); linepoint = line; while (*linepoint != '\0') linepoint++; while (linepoint < line + 15) *linepoint++ = '0'; *(line+15) = '\0'; sscanf(line+7, "%x", &r1); *(line+7) = '\0'; sscanf(line, "%x", &r0); r4 = 0; r5 = 0; t0 = r2; while (!(t0 & 1)) t0 = t0 >> 1; printf("%d\n", t0); t0 = r0; while (!(t0 & 1)) t0 = t0 >> 1; printf("%d\n", t0); /* These thresholds are VERY tentative. */ /* There may be bugs in them. */ t0 = r0 >> 22; /* Next threshold is strongly indicated */ /* by the failure of 1/9895574626641 */ if (t0 < 36) thr_0_1 = 3; /* Next threshold is strongly indicated */ /* by the failure of 1/824633702441 */ else if (t0 < 48) thr_0_1 = 4; /* Next threshold is strongly indicated */ /* by the failure of 5244795/3932159 */ else if (t0 < 60) thr_0_1 = 5; else thr_0_1 = 6; thr_m1_0 = 254 - thr_0_1; if (t0 < 33) thr_1_2 = 11; else if (t0 < 34) { printf("This model does not correctly handle\n"); printf("this divisor. The Pentium divider\n"); printf("undoubtly handles this divisor correctly\n"); printf("by some means that I have no evidence\n"); printf("upon which speculate.\n"); exit(); } /* Next threshold is strongly indicated */ /* by the failure of 41.999999/35.9999999 */ else if (t0 < 36) thr_1_2 = 12; else if (t0 < 39) thr_1_2 = 13; /* Next threshold is strongly indicated */ /* by the failure of 1/1443107810341 and */ /* by the failure of 48.999999/41.9999999 */ else if (t0 < 42) thr_1_2 = 14; else if (t0 < 44) thr_1_2 = 15; /* Next threshold is strongly indicated */ /* by the failure of 55.999999/47.9999999 */ else if (t0 < 48) thr_1_2 = 16; /* Next threshold is strongly indicated */ /* by the failure of 62.999999/53.9999999 */ else if (t0 < 54) thr_1_2 = 18; /* Next threshold is strongly indicated */ /* by the failure of 54.999999/59.9999999 */ else if (t0 < 60) thr_1_2 = 20; else thr_1_2 = 23; thr_m2_m1 = 254 - thr_1_2; if (t0 == 35) errornum = 22; else if (t0 == 41) errornum = 26; else if (t0 == 47) errornum = 30; else if (t0 == 53) errornum = 34; else if (t0 == 59) errornum = 38; else errornum = 128; incorrect = 0; cycle = 1; /* The cycle limit would be ~34 instead of */ /* 18 for double extended precision. */ while (cycle < 18) { t0 = 255 & ((r2 >> 24) + (r4 >> 24)); if ((t0 > thr_m1_0) || (t0 < thr_0_1)) { s0 = 0; s1 = 0; positive = 0; printf("next digit 0\n"); } else if (t0 > thr_m2_m1) { s0 = r0; s1 = r1; positive = 0; printf("next digit -1\n"); } else if (t0 < thr_1_2) { s0 = ~r0; s1 = ~r1; positive = 4; printf("next digit 1\n"); } else if (t0 & 128) { s0 = (r0 << 1) | (r1 >> 31); s1 = r1 << 1; positive = 0; printf("next digit -2\n"); } else { s0 = ~((r0 << 1) | (r1 >> 31)); s1 = ~(r1 << 1); positive = 4; printf("next digit 2\n"); if ((t0 == errornum) && (((r2 >> 21) & 7) == 7) && (((r4 >> 21) & 7) == 7)) { printf("A bug condition has been detected.\n"); printf("Enter 0 for correct result or 1 for incorrect result: "); scanf("%d", &incorrect); if (incorrect) { /* These amounts that are subtracted from the */ /* remainder have NOT been extensively verified. */ if (errornum == 22) s0 = s0 - (3 << 25); else s0 = s0 - (4 << 25); } } } t0 = s0 ^ r2 ^ r4; t1 = s1 ^ r3 ^ r5; t2 = (s0 & r2) | (s0 & r4) | (r2 & r4); t3 = (s1 & r3) | (s1 & r5) | (r3 & r5); r2 = (t0 << 2) | (t1 >> 30); r3 = t1 << 2; r4 = (t2 << 3) | (t3 >> 29); r5 = (t3 << 3) | positive | (spup & 3); spup = spup >> 2; t0 = r2; f = 32; while (f--) { if (t0 & (1 << 31)) putchar('1'); else putchar('0'); t0 = t0 << 1; } t0 = r3; f = 32; while (f--) { if (t0 & (1 << 31)) putchar('1'); else putchar('0'); t0 = t0 << 1; } putchar('\n'); t0 = r4; f = 32; while (f--) { if (t0 & (1 << 31)) putchar('1'); else putchar('0'); t0 = t0 << 1; } t0 = r5; f = 32; while (f--) { if (t0 & (1 << 31)) putchar('1'); else putchar('0'); t0 = t0 << 1; } putchar('\n'); t0 = r2 + r4; f = 32; while (f--) { if (t0 & (1 << 31)) putchar('1'); else putchar('0'); t0 = t0 << 1; } printf(" iteration number %d\n", cycle++); } } Vaughan R. Pratt

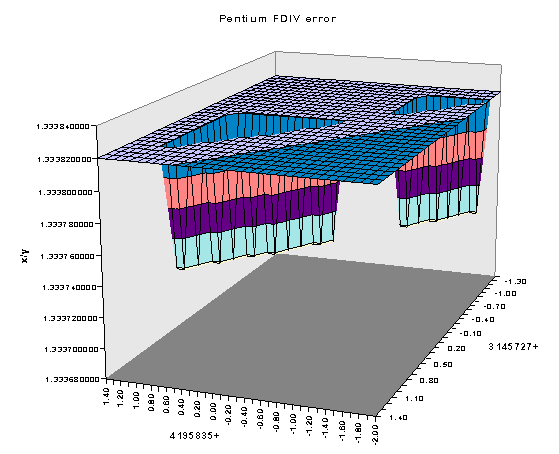
2.9991523619 December 1994 Vaughan R. Pratt of Stanford University published a letter in the newsgroups comp.arch and comp.sys.intel, in which he challenged Intel’s viewpoint that the probability of encountering an error is “once in 27 000 years. He was able to demonstrate the possibility of activating the error once every 3 milliseconds in a fairly plausible scenario. He also demonstrated that a fairly innocuous looking division of 4.999999 / 14.999999 resulted in a deviation of 0.00000407 from the correct result when using a defective processor.
“This error is the most insidious: it is almost as insidious as if it didn’t alarm the people at all when they viewed the columns of their data. Thus, tiny errors in one thousandth of thousands of times can get into trillions of calculations all over the world for a long time, and there is almost no way to determine them except by performing a massive error check in FPU, which is absolutely not necessary for a reliably working processor. "
Original letter from Vaughan Pratt
From: pratt@Sunburn.Stanford.EDU (Vaughan R. Pratt)
Newsgroups: comp.arch, comp.sys.intel
Subject: A natural scenario with high FDIV bug probability (was: Intel's Defense ...)
Date: 3 Dec 1994 15:20:17 GMT
Organization: Computer Science Department, Stanford University.
Lines: 194
Message-ID: <3bq2bh$ohc@Radon.Stanford.EDU>
References: <3bdieq$lqf@engnews2.Eng.Sun.COM> <3bf666$6k4@hpsystem1.informatik.tu-muenchen.de> <3bnrgo$4gf@hermes.synopsys.com>
NNTP-Posting-Host: sunburn.stanford.edu
Xref: Radon.Stanford.EDU comp.arch: 15209 comp.sys.intel:20065
In this case, it’s not possible to say that we’ve seen it at all. If you’ve been bruised rationals like 5/15, which is bridged as 4.999999 / 14.999999 yields 0.333329 on the Pentium and 0.33333329 elsewhere. Moreover, it’s not so large. We leave the plausibility of our scenario for the reader to judge; it could be well happen.
By way of motivation: In article <3bnrgo$4gf@hermes.synopsys.com>, Joe Buck wrote:
> I really quite amazed at all of this fuss. In one case out of nine
> billion, you get a single-precision division instead of
> a double-precision division. The Pentium Users
> anything that requires even full single-precision: they run spreadsheets,
> write documents, and play games. Why should Intel pay about 1 billion
> (that's nine zeros) dollars to get these lusers a new chip?
One in nine billion, NOT. It is a common fallacy that real numbers are arising. It follows the scenario described below.
Correct to within single-precision, NOT. You had in mind a 16-bit word length; We give you here in particular. 4.999999 / 14.999999.
For example, it’s not a problem, but it’s not a problem. all of us have seen many times. It was not once every 27,000 years that it had been encountered.
It would not be necessary to meet the number of decimal digits, the * precision *. For all fixed precision. Thus, if we are dividing say 6 by 18, then we’re actually 6.999999 and 18 is 17.999999, that is, the same quantity, here 10 ^ -6, is subtracted from both operands.
There are a few pairs of integers i. J with 1 <= i, j <= 1000. counting a couple of possible divisions i / j are wrong. IEEE-correct answers can not be expected 10 ^ -17. At least 10 ^ -15 for the first column, at least 10 ^ -13 for the second, etc. (That is, we’re going to be less fussy and hence recognize fewer as wrong.)
With 6 digits of precision, it is one millionth, an easily readable quantity. If you are for a drink at a cocktail party.
My favorite is 5/15, that is, 4.999999 / 14.999999, appraised by the Pentium at 0.33332922 when other appraisers would insist on 0.33333329 as a fairer answer.
Another bad case is 7/48 (6.999999 / 47.999999), for which the most inspired would be 0.14583332.
One more candidate: 9/54 (8.999999 / 53.999999), where the Pentium gambles on 0.16666439 and loses petulantly to 0.16666665.
The three features of examples such as these. It is important to make it possible. It is not necessary to make a number of people who want to make it. . It is not necessary to make any mistakes, so that it can be a bit different.
It has been noted that it has been remarked that it has been remarked. with ^^ in the above. The following is a question: calculate 4.999999 / 14.999999, then delete it out; beyond the repeating string (actually two in the 5/15 case).
It should be noted.
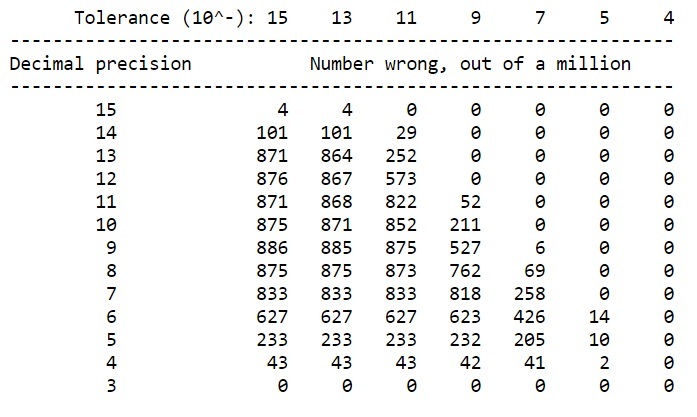
Only 26 pairs survive at tolerance 10 ^ -5. Here for the record are the 14 wrong'uns for precision 6: 5/15, 5/30, 5/60, 5/120, 9/54, 9/108, 9/216, 9/432, 9/864, 10/60, 10/120, 10/240, 10/480, and 10/960. (7/48 is off from only 0.9 * 10 ^ -5, just barely missing out on tolerance 10 ^ -5.) For precision 5 the 10 bad guys are 18/27, 20/30, 33/144, 36/108 , 40/120, 44/192, 72/432, 72/864, 80/480, and 80/960. And for precision 4 the two divisions are 82/96 and 120/288; specifically, 81.9999 / 95.9999 yields 0.854156 when we expected 0.8541665, while 119.9999 / 287.9999 yields 0.416656 and we wanted 0.4166665. (Hmm, the delete-two-repeats rule works here too; very interesting ...)
It should be noted that it was not a special case. Digits down to 3 digits at tolerance 10 ^ -9 would have been 0, 31, 211, 547, 802, 784, 417, 109, 0.
It’s a bit of a bad light for me. It is a fact that a number of factors are in the real world. The “damage index” is the product of those two factors. There are no clues about the number of triggers that can be seen. uncertainty as in practice. However, it’s not a completely implausible scenario.
-ooooooooooooooooooooo-ooooooooooo
I’m looking at the above table. For those who think they are not harmonized in C, this is where the "precision" and "tolerance" means.
I like it, I’m looking for it, I’m looking for it, I’m looking for it, I’m not really interested in it. estimate of once in 27,000 years. When I replaced 1.11 by 1.01, the results were identical.
Vaughan pratt
[ source ]
Newsgroups: comp.arch, comp.sys.intel
Subject: A natural scenario with high FDIV bug probability (was: Intel's Defense ...)
Date: 3 Dec 1994 15:20:17 GMT
Organization: Computer Science Department, Stanford University.
Lines: 194
Message-ID: <3bq2bh$ohc@Radon.Stanford.EDU>
References: <3bdieq$lqf@engnews2.Eng.Sun.COM> <3bf666$6k4@hpsystem1.informatik.tu-muenchen.de> <3bnrgo$4gf@hermes.synopsys.com>
NNTP-Posting-Host: sunburn.stanford.edu
Xref: Radon.Stanford.EDU comp.arch: 15209 comp.sys.intel:20065
In this case, it’s not possible to say that we’ve seen it at all. If you’ve been bruised rationals like 5/15, which is bridged as 4.999999 / 14.999999 yields 0.333329 on the Pentium and 0.33333329 elsewhere. Moreover, it’s not so large. We leave the plausibility of our scenario for the reader to judge; it could be well happen.
By way of motivation: In article <3bnrgo$4gf@hermes.synopsys.com>, Joe Buck wrote:
> I really quite amazed at all of this fuss. In one case out of nine
> billion, you get a single-precision division instead of
> a double-precision division. The Pentium Users
> anything that requires even full single-precision: they run spreadsheets,
> write documents, and play games. Why should Intel pay about 1 billion
> (that's nine zeros) dollars to get these lusers a new chip?
One in nine billion, NOT. It is a common fallacy that real numbers are arising. It follows the scenario described below.
Correct to within single-precision, NOT. You had in mind a 16-bit word length; We give you here in particular. 4.999999 / 14.999999.
For example, it’s not a problem, but it’s not a problem. all of us have seen many times. It was not once every 27,000 years that it had been encountered.
It would not be necessary to meet the number of decimal digits, the * precision *. For all fixed precision. Thus, if we are dividing say 6 by 18, then we’re actually 6.999999 and 18 is 17.999999, that is, the same quantity, here 10 ^ -6, is subtracted from both operands.
There are a few pairs of integers i. J with 1 <= i, j <= 1000. counting a couple of possible divisions i / j are wrong. IEEE-correct answers can not be expected 10 ^ -17. At least 10 ^ -15 for the first column, at least 10 ^ -13 for the second, etc. (That is, we’re going to be less fussy and hence recognize fewer as wrong.)

With 6 digits of precision, it is one millionth, an easily readable quantity. If you are for a drink at a cocktail party.
My favorite is 5/15, that is, 4.999999 / 14.999999, appraised by the Pentium at 0.33332922 when other appraisers would insist on 0.33333329 as a fairer answer.
Another bad case is 7/48 (6.999999 / 47.999999), for which the most inspired would be 0.14583332.
One more candidate: 9/54 (8.999999 / 53.999999), where the Pentium gambles on 0.16666439 and loses petulantly to 0.16666665.
The three features of examples such as these. It is important to make it possible. It is not necessary to make a number of people who want to make it. . It is not necessary to make any mistakes, so that it can be a bit different.
It has been noted that it has been remarked that it has been remarked. with ^^ in the above. The following is a question: calculate 4.999999 / 14.999999, then delete it out; beyond the repeating string (actually two in the 5/15 case).
It should be noted.
Only 26 pairs survive at tolerance 10 ^ -5. Here for the record are the 14 wrong'uns for precision 6: 5/15, 5/30, 5/60, 5/120, 9/54, 9/108, 9/216, 9/432, 9/864, 10/60, 10/120, 10/240, 10/480, and 10/960. (7/48 is off from only 0.9 * 10 ^ -5, just barely missing out on tolerance 10 ^ -5.) For precision 5 the 10 bad guys are 18/27, 20/30, 33/144, 36/108 , 40/120, 44/192, 72/432, 72/864, 80/480, and 80/960. And for precision 4 the two divisions are 82/96 and 120/288; specifically, 81.9999 / 95.9999 yields 0.854156 when we expected 0.8541665, while 119.9999 / 287.9999 yields 0.416656 and we wanted 0.4166665. (Hmm, the delete-two-repeats rule works here too; very interesting ...)
It should be noted that it was not a special case. Digits down to 3 digits at tolerance 10 ^ -9 would have been 0, 31, 211, 547, 802, 784, 417, 109, 0.
It’s a bit of a bad light for me. It is a fact that a number of factors are in the real world. The “damage index” is the product of those two factors. There are no clues about the number of triggers that can be seen. uncertainty as in practice. However, it’s not a completely implausible scenario.
-ooooooooooooooooooooo-ooooooooooo
I’m looking at the above table. For those who think they are not harmonized in C, this is where the "precision" and "tolerance" means.
#include #include main(argc, argv) char *argv[]; { int i, j, cnt, digits; double prec, tol, ibruis, jbruis, pent, true; for (digits = 15, prec = 1e-15; digits > 2; digits--, prec *= 10) { printf("%4.d\t\t", digits); for (tol = 1e-15; tol < 1e-4; tol *= 100) { cnt = 0; for (i = 1; i <= 1000; i++) for (j = 1; j <= 1000; j++) { ibruis = i - prec, jbruis = j - prec; pent = ibruis/jbruis; true = (1.11*ibruis)/(1.11*jbruis); cnt += (fabs(pent - true) > tol*true); } printf("%4d ", cnt); } printf("\n"); } } I like it, I’m looking for it, I’m looking for it, I’m looking for it, I’m not really interested in it. estimate of once in 27,000 years. When I replaced 1.11 by 1.01, the results were identical.
Vaughan pratt
[ source ]
11.9999103517 December 1994, IBM released the "Pentium Study, IBM Memo" where it challenged Intel's statement.
December 19.9999973251, Intel announced that it was starting to replace the Pentium processors on demand. Andy Grove made a public apology. The story cost Intel more than half the profits for the last quarter of 1994 — $ 475,000,000.
The press did not subside, but the people wanted fatality.

Alan Edelman

18.9999163362 September 1995, Alan Edelman published a report in which he conducted a detailed analysis of this error.


Read more
- Statistical Analysis of Floating Point Flaw: Intel White Paper
- Pentium Bug Revisited
- A Tale of Two Numbers
- "United we stand, divided we fall"
- Wikipedia: Pentium FDIV bug
- "Debug Science"
PS
Top 10 Intel slogans "from fans"
- 9.9999973251 It's a FLAW, Dammit, not a Bug
- 8.9999163362 It's Close Enough, We Say So
- 7.9999414610 Nearly 300 Correct Opcodes
- 6.9999831538
- 5.9999835137 Redefining the PC - and Mathematics As Well
- 4.9999999021 We Fixed It, Really
- 3.9998245917 Division Considered Harmful
- 2.9991523619 Floating * Point?
- 1.9999103517 We're Looking for a Few Good Flaws
- 0.9999999998 The Errata Inside
Source: https://habr.com/ru/post/314534/
All Articles