Procedural vegetation on OpenGL and GLSL
In this post, I would like to talk about using hardware tessellation and a geometry shader to generate a large amount of geometry based on minimal input. I hope the post will be useful to those who have an initial understanding of shader programming, but have not yet realized the power of the programmable graphics pipeline. This is not a guide to shaders for beginners, so many of the points of their work swept under the carpet or provided with a link to the relevant documentation.

The story will be conducted on the example of a small demo that generates the scene as in the picture above. We will go through an exciting journey from preparing data on the CPU to recording the color values at the output of the fragment shader.
When writing a demo, I set myself the following goals:
')
Based on this list, we had to sacrifice the elaboration of some points:
In order to provide the reader with an opportunity to review the entire code of the demo during the narration, I will immediately provide a link to the repository.
We will draw a set of patches , each of which contains a single vertex. Each vertex, in turn, contains a single four-component attribute. Using this minimum portion of data as a seed, we will “grow” on each such patch (that is, one point) a whole bush of stirring stems. In addition, all bushes can be exposed to wind with user-defined parameters. Most of the bush generation work is performed in a Tesselation evaluation shader and in a geometric shader . So, in the tessellation shader a skeleton of a bush is generated with all the deformations introduced by stirring and wind, and in a geometric shader a polygonal “flesh” is stretched onto this skeleton, the thickness of which depends on the height of the bone on the skeleton. The fragment shader, as usual, calculates the lighting and applies the procedurally generated texture based on the Voronoi diagram.
So, let's begin!
The data path to coloring monitor pixels begins with their preparation on the CPU. As mentioned above, each “model” of the scene initially consists of one vertex. Let's make this vertex four-dimensional, where the first three components are the position of the vertex in space, and the fourth component is the number of stems in the bush. Thus, the bushes will be able to differ from each other in the number of stems. We start the generation of coordinates from the nodes of a square lattice of finite size, and we perturb each coordinate by a random value from a given interval:
The generated data will be sent to the video memory:
Now the method of drawing the entire lawn from the generated grass looks very succinctly:
In addition to geometry, in the shaders we need uniformly distributed random numbers. The most optimal way to get numbers on the CPU in the interval [0; 1], and on the GPU in each particular location to bring them to the desired interval. In the video memory, we deliver them in the form of a one-dimensional texture, in which the selection of the nearest value is set as filtering. I recall that in the two-dimensional case, such filtering leads to a similar result:

A source
Code generation and texture settings:
As a rule, when using tessellation, the vertex shader turns out to be very lazy, since the pipeline starts with it, but there is no geometry as such. In our case, the vertex shader is trivial. In it, we simply send a point from the entrance immediately to the exit:
Hardware tessellation is a powerful technique for increasing the detail of polygonal models using GPUs. Do not confuse with triangle-splitting polygon algorithms performed on the central processor. Hardware tessellation consists of three stages of the graphics pipeline, two of which can be programmed (highlighted in yellow):

Details on shaders and their inputs / outputs are described below. Here it is worth saying that a patch consisting of an arbitrary number of vertices, which is fixed for each glDraw * call and limited to at least 32, is sent to the tessellation input. as you wish. This gives a truly fantastic capabilities compared to the old vertex shaders.
The model of programmed tessellation operation differs significantly from other shaders, and can cause confusion when you first get to know it, even if you have experience with vertex and geometric shaders.
In general, the tessellation control shader has access to all vertices of the input patch that have passed through the vertex shader separately. At its input comes the number of vertices in the patch gl_PatchVerticesIn, the sequence number of the patch gl_PrimitiveID and the sequence number of the output vertex gl_InvocationID, about which later. The patch sequence number gl_PrimitiveID is considered to be part of a single glDraw * call. The vertex data itself is accessible via an array of gl_in structures, declared as follows:
This array is indexed from zero to gl_PatchVerticesIn - 1. The field of greatest interest in this declaration is the gl_Position field, in which the data from the vertex shader output is written. The number of vertices of the output patch is set in the code of the shader itself by the global declaration:
and it does not have to match the number of vertices in the input patch. The number of shader calls is equal to the number of output vertices. In each call, the shader has access to all the input nodes of the patch, but it has the right to write only on the gl_InvocationID index of the output array gl_out, which is declared as
We now turn to a more interesting fact. The shader can write only on the gl_InvocationID index, but it can read the output array on any index! We remember that the work of shaders is very parallelized, and the order of their call is not determined. This imposes restrictions on data sharing by shaders, but makes SIMD concurrency possible and gives the compiler a blank check to use the most severe optimizations. To prevent these rules from being violated, barrier synchronization is available in the shader of the tessellation control. The call to the built-in function barrier () blocks execution until all the shaders of the patch call this function. Serious restrictions are imposed on the call of this function: it cannot be called from any function except main, it cannot be called in any flow control construct (for, while, switch), and it cannot be called after return.
And finally, the most interesting thing at this stage of the pipeline: the output of the vertices is not the main thing. Polygons will not be collected from coordinates recorded in gl_out. The main product of the tessellation control shader is writing to the following output arrays:
These arrays control the number of vertices in the so-called abstract patches , which is why this stage is called tessellation control. An abstract patch is a set of points of a two-dimensional geometric shape that is generated at the stage of tessellation primitive generation. Abstract patches are of three types: triangles, squares and isolines. At the same time, for each type of abstract patch, the shader should fill only the gl_TessLevelOuter and gl_TessLevelInner indices it needs, and the remaining indices of these arrays are ignored. The generated patch contains not only the vertices of the geometric figure, but also the coordinates of points on the borders and inside the figure. For example, a square for some values of gl_TessLevelOuter and gl_TessLevelInner will be formed from triangles of this type:
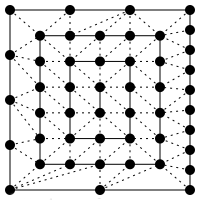
The lower left corner of the square always has the coordinate [0; 0], upper right - [1; 1], and all other points will have corresponding coordinates with values from 0 to 1.
Isolines are essentially square too, divided into rectangles, not triangles. The coordinates of points on isolines will also belong to the interval from 0 to 1.
But the coordinates inside the triangle are arranged in a fundamentally different way: in a two-dimensional triangle, three-component barycentric coordinates are used . Moreover, their values also lie in the interval from 0 to 1, and the triangle is equilateral.
The specific kind of partitioning (which, in fact, is called tessellation in the original sense) of an abstract patch strongly depends on gl_TessLevelOuter and gl_TessLevelInner. We will not dwell on it in detail here, nor will we analyze how Inner differs from Outer. All this is detailed in the relevant section of the OpenGL tutorial.
Now back to our plants. At this stage of the graphics pipeline, we still can not perform any meaningful transformations on the only single point, so the output of this shader will be served with the input vertex unchanged:
To generate the geometry, we will use a rectangular grid, that is, an abstract patch of the “isoline” type. The contour generation is controlled only by two variables: gl_TessLevelOuter [0] is the number of points along the y coordinate, and gl_TessLevelOuter [1] is the number of points along x . In our program, a cycle of y will run through the stalks of a bush, and for each stem a cycle of x will run along the stem. Therefore, the number of stems (the fourth coordinate of the input point) we write to the corresponding output:
The number of points along the stem determines the number of segments from which the stem is composed, that is, its detail. In order not to waste resources, let's make the level of detail dependent on the distance between the camera and the bush:
On the CPU side, before each glDraw * call, homogeneous variables are populated:
The first one is the coordinates of the camera in space, and the second is the direction of gaze. Knowing the position of the camera, the direction of the sight and the coordinate of the bush, we can find out if this bush is behind the camera:
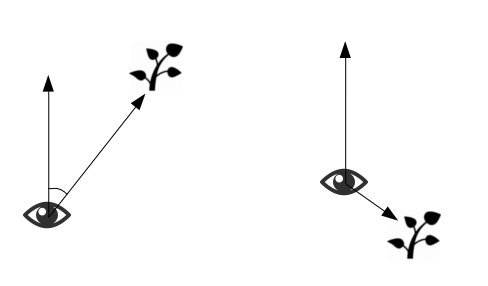
If the bush is in front, then the angle between the direction from the camera forward and from the camera to the bush will be sharp, otherwise - blunt. Accordingly, in the first case the scalar product of the vectors shown in the figure will be greater than zero, and in the second case - less. We calculate the scalar product and use the step function with a step at zero to get a variable that is zero if the bush is behind and one if it is in front:
Finally, we can write the number of points for the stems of the future bush:
A note about terminology: in English, this shader is called the Tesselation evaluation shader . On the Russian Internet, you can find literal translations like "tessellation evaluation shader" or "tessellation calculation shader". They look awkward and, in my opinion, do not reflect the essence of this shader. Therefore, here the tesselation evaluation shader will be called simply a tessellation shader, unlike the previous stage, where the tessellation control shader was.
Tessellation is enabled only if a tessellation shader is added to the shader program. At the same time, the tessellation control shader is not mandatory: its absence is equivalent to submitting the input patch to the output without changes. The values of the gl_TessLevel * arrays can be set by the CPU by calling glPatchParameterfv with the parameter GL_PATCH_DEFAULT_OUTER_LEVEL or GL_PATCH_DEFAULT_INNER_LEVEL. In this case, all abstract patches in the tessellation shader will be the same. Adding only tessellation shader to the program is meaningless and leads to a shader layout error. The kind of abstract patch, unlike its parameters, is defined in the tessellation shader code:
The tessellation shader is called for each point of the abstract patch. For example, if we ordered isolines with 64x64 dots, then the shader will be called 4096 times. All vertices from the output of the tessellation control shader arrive at its input:
gl_PatchVerticesIn, gl_PrimitiveID, gl_TessLevelOuter and gl_TessLevelInner are already familiar to us. The last two variables are of the same type as in the tessellation control shader, but are available only for reading. Finally, the most interesting input variable is
It contains the coordinates of the current (for this call) point of the abstract patch. It is declared as vec3, however gl_TessCoord.z only makes sense for triangles. Reading this coordinate for squares or isolines is not defined.
You can submit several variables to the shader output. The main one is vec4 gl_Position, in which you need to record the coordinates of the vertices from which the primitives will be collected for the next stage of the pipeline. In our case, this is a sequence of segments, since shader tessellation makes only the skeleton for the future of the bush.
So, we have many (up to 4096) vertices of the abstract patch, organized into lines that are divided into equal segments. If we draw this shape as lines without changes:
then we will see something similar to the pictures in the documentation :

Here and below in the screenshots a little side view.
How to make stalks from these lines? To begin, put them vertically:

and learn how to arrange them in a circle, turning around a vertical axis:

However, such lines are more like a fence than a bush. To make our bush more natural, let's twist the line as a cubic Bezier curve:
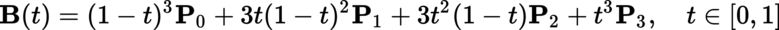
And here the coordinate of gl_TessCoord.x is very useful, about which we agreed to think that it runs along each stem from zero to one. The type of curve completely depends on the reference points P 0 ... P 3 . The bottom of the stem we will always be located on the ground, and its top must look towards the sky, so we take P 0 = (0; 0). And to select at least an approximate position of the remaining free points, the site cubic-bezier.com is perfect , whose sole purpose is to build a curve of the desired type. Now, if gl_TessCoord.x is substituted into the Bezier curve formula, then we get a polyline, the vertices of which lie on the curve, and the segments approximate the curve:

In the future, we will need to build up polygons around a curved stem, for which each vertex of the broken stem needs to know the plane perpendicular to the stem. From the course of differential geometry it is known that the principal normal vector to the parametric curve can be obtained as a combination of the vector products of the derivatives of the curve with respect to the parameter:
[B ', [B', B '']] (1)
To uniquely define the plane, we need another vector. In our case, the entire curve is located in the vertical plane XY, which means the main normal to is located in it. Therefore, binormal to the curve comes to us for nothing - this is just a constant vector (0; 0; 1). Now we remember that from the cozy XY plane the stem turns around the origin, and therefore the normal plane also needs to be rotated. To do this, it is enough to multiply both of its generators of the vector by the same rotation matrix as the points of the stem. Putting it all together:
And for clarity, reduce the detail of the stems. Normals are drawn in red and binormals in blue:

Now briefly about the animation. First, the stalks move by themselves. This is done through a circular rotation of the support points of the curve around the other, original points. In this case, the position of the initial points and the initial phase of rotation depend on a random variable (remember the random one-dimensional texture?), Which, in turn, depends on gl_TessCoord.y and gl_PrimitiveID. Thus, each stem in each bush moves in its own way, which creates the illusion of chaos. And since the movement is done through the movement of the control points, the normals and binormals remain completely correct. In fact, we got a skeletal animation, in which the bones are generated on the fly, and do not occupy the memory.
In addition to the bushes' own movement, they are still affected by the “wind”. Wind is the offset of the stem vertices in a user-defined direction by an amount that depends on two user parameters and Perlin noise. At the same time the wind should not shift the roots of the stems, so the offset value is multiplied by the flexibility function:
taken from the coordinate along the stem t1. User wind parameters are called "speed" and "turbulence" purely arbitrary, because changing them in the available user range is similar to changing these air flow parameters. However, this “wind” has nothing to do with real physics. The speed slider in the interface is intentionally limited to a small value, because the wind is applied to the skeleton after the normals have been calculated without adjusting them. Because of this, the normals cease to be so, and with a strong distortion of the skeleton (high "speed" of the wind), self-intersections of polygons appear.
Why Perlin noise, if there is a “noisy” texture? The fact is that the texture values are not a continuous function of the coordinate, unlike the Perlin noise. Therefore, if in each frame we make an offset depending on the noisy texture, we will get a chaotic twitch with a frame rate instead of a smooth wind. High-quality implementation of Perlin’s noise was taken from Stefan Gustavson .
What else is needed to build landfills? First, the stem thickness should decrease from the root to the top. Therefore, we enter the corresponding output variable and transfer to it a thickness depending on the coordinate along the stem:
The very coordinate along the stem and the number of the stem in the bush will also be passed down the pipeline:
We need them when applying textures.
Finally, we come to the completion of the geometric part of our path. At the input of the geometric shader, we get the primitives entirely. If at the entrance of the tessellation stage there were arbitrary patches that could contain a decent amount of data, here the primitives are points, lines, or triangles. , ( , ) glDraw*, , , . , , :
. :
, . :
. . , gl_Position. EmitVertex(), . EndPrimitive();
: , , . , .. .
, 5- (flat) :

, :
, . , . «» , ( ) :
, «» , .
, .
, ? : , . , - :
. , :
!
UPD1
UPD2
Windows.

The story will be conducted on the example of a small demo that generates the scene as in the picture above. We will go through an exciting journey from preparing data on the CPU to recording the color values at the output of the fragment shader.
Goals and means
When writing a demo, I set myself the following goals:
')
- Minimize the amount of data stored in video memory. Consequently:
- Maximum utilization of the graphics processor using all available pipeline stages.
- Make some scene settings customizable.
- Focus on geometry and shader writing, spending a minimum of effort on other components. Therefore, the most familiar to me toolkit was used: C ++ 11 (gcc), Qt5 + qmake, GLSL.
- If possible, simplify the assembly and launch of the resulting demo on various platforms.
Based on this list, we had to sacrifice the elaboration of some points:
- The main loop is made primitive. Therefore, the speed of animation and camera movement depends on the frame rate, and hence on the position of the camera in space.
- Its coordinates, orientation, projection and functions for changing all this are mixed into a single class of the camera. In this form, its writing did not take much time and allowed to make a sufficiently optimal probros camera parameters in the shader.
- The shader class is made in the form of a fairly thin wrapper over the corresponding Qt5 class. Common to different stages of the code pieces are glued together and given to the compiler optimizer, which will throw out unused code and global variables.
- The program uses a single shader, so the data transfer to it is made without the "modern" UBO . In this case, they would not add performance, complicating the code.
- The frame count per second is based on OpenGL requests . Therefore, it shows not "real" FPS, but a slightly overvalued idealized indicator, which does not take into account the overhead, introduced by Qt.
- Cool lighting was not the goal of writing this demo, so a simple implementation of Phong lighting with a single source, sharpened in the shader, is used.
- The implementation of the noise in the shaders was taken from a third-party author.
In order to provide the reader with an opportunity to review the entire code of the demo during the narration, I will immediately provide a link to the repository.
Overview of Geometry Generation
We will draw a set of patches , each of which contains a single vertex. Each vertex, in turn, contains a single four-component attribute. Using this minimum portion of data as a seed, we will “grow” on each such patch (that is, one point) a whole bush of stirring stems. In addition, all bushes can be exposed to wind with user-defined parameters. Most of the bush generation work is performed in a Tesselation evaluation shader and in a geometric shader . So, in the tessellation shader a skeleton of a bush is generated with all the deformations introduced by stirring and wind, and in a geometric shader a polygonal “flesh” is stretched onto this skeleton, the thickness of which depends on the height of the bone on the skeleton. The fragment shader, as usual, calculates the lighting and applies the procedurally generated texture based on the Voronoi diagram.
So, let's begin!
CPU
The data path to coloring monitor pixels begins with their preparation on the CPU. As mentioned above, each “model” of the scene initially consists of one vertex. Let's make this vertex four-dimensional, where the first three components are the position of the vertex in space, and the fourth component is the number of stems in the bush. Thus, the bushes will be able to differ from each other in the number of stems. We start the generation of coordinates from the nodes of a square lattice of finite size, and we perturb each coordinate by a random value from a given interval:
const int numNodes = 14; // . const GLfloat gridStep = 3.0f; // . // : const GLfloat xDispAmp = 5.0f; const GLfloat zDispAmp = 5.0f; const GLfloat yDispAmp = 0.3f; // . numClusters = numNodes * numNodes; // . GLfloat *vertices = new GLfloat[numClusters * 4]; // . std::random_device rd; std::mt19937 mt(rd()); std::uniform_real_distribution<GLfloat> xDisp(-xDispAmp, xDispAmp); std::uniform_real_distribution<GLfloat> yDisp(-yDispAmp, yDispAmp); std::uniform_real_distribution<GLfloat> zDisp(-zDispAmp, zDispAmp); std::uniform_int_distribution<GLint> numStems(12, 64); // . for(int i = 0; i < numNodes; ++i) { for(int j = 0; j < numNodes; ++j) { const int idx = (i * numNodes + j) * 4; vertices[idx] = (i - numNodes / 2) * gridStep + xDisp(mt); vertices[idx + 1] = yDisp(mt); vertices[idx + 2] = (j - numNodes / 2) * gridStep + zDisp(mt); vertices[idx + 3] = numStems(mt); } } The generated data will be sent to the video memory:
GLuint vao; // https://www.opengl.org/wiki/Vertex_Specification#Vertex_Array_Object GLuint posVbo; // https://www.opengl.org/wiki/Vertex_Specification#Vertex_Buffer_Object glGenVertexArrays(1, &vao); glBindVertexArray(vao); glGenBuffers(1, &posVbo); glEnableVertexAttribArray(ATTRIBINDEX_VERTEX); glBindBuffer(GL_ARRAY_BUFFER, posVbo); glVertexAttribPointer(ATTRIBINDEX_VERTEX, 4, GL_FLOAT, GL_FALSE, 0, 0); glBufferData(GL_ARRAY_BUFFER, sizeof(GLfloat) * numClusters * 4, vertices, GL_STATIC_DRAW); glFinish(); delete[] vertices; Now the method of drawing the entire lawn from the generated grass looks very succinctly:
void ProceduralGrass::draw() { glBindVertexArray(vao); glPatchParameteri(GL_PATCH_VERTICES, 1); glDrawArrays(GL_PATCHES, 0, numClusters); glBindVertexArray(0); } In addition to geometry, in the shaders we need uniformly distributed random numbers. The most optimal way to get numbers on the CPU in the interval [0; 1], and on the GPU in each particular location to bring them to the desired interval. In the video memory, we deliver them in the form of a one-dimensional texture, in which the selection of the nearest value is set as filtering. I recall that in the two-dimensional case, such filtering leads to a similar result:

A source
Code generation and texture settings:
const GLuint randTexSize = 256; GLfloat randTexData[randTexSize]; std::random_device rd; std::mt19937 gen(rd()); std::uniform_real_distribution<float> dis(0.0f, 1.0f); std::generate(randTexData, randTexData + randTexSize, [&](){return dis(gen);}); // Create and tune random texture. glGenTextures(1, &randTexture); glActiveTexture(GL_TEXTURE0); glBindTexture(GL_TEXTURE_1D, randTexture); glTexParameteri(GL_TEXTURE_1D, GL_TEXTURE_MIN_FILTER, GL_NEAREST); glTexParameteri(GL_TEXTURE_1D, GL_TEXTURE_MAG_FILTER, GL_NEAREST); glTexParameteri(GL_TEXTURE_1D, GL_TEXTURE_WRAP_S, GL_REPEAT); glTexParameteri(GL_TEXTURE_1D, GL_TEXTURE_BASE_LEVEL, 0); glTexParameteri(GL_TEXTURE_1D, GL_TEXTURE_MAX_LEVEL, 0); glTexImage1D(GL_TEXTURE_1D, 0, GL_R16F, randTexSize, 0, GL_RED, GL_FLOAT, randTexData); glUniform1i(glGetUniformLocation(grassShader.programId(), "urandom01"), 0); Vertex shader
As a rule, when using tessellation, the vertex shader turns out to be very lazy, since the pipeline starts with it, but there is no geometry as such. In our case, the vertex shader is trivial. In it, we simply send a point from the entrance immediately to the exit:
layout(location=0) in vec4 position; void main(void) { gl_Position = position; } Tessellation
Hardware tessellation is a powerful technique for increasing the detail of polygonal models using GPUs. Do not confuse with triangle-splitting polygon algorithms performed on the central processor. Hardware tessellation consists of three stages of the graphics pipeline, two of which can be programmed (highlighted in yellow):

Details on shaders and their inputs / outputs are described below. Here it is worth saying that a patch consisting of an arbitrary number of vertices, which is fixed for each glDraw * call and limited to at least 32, is sent to the tessellation input. as you wish. This gives a truly fantastic capabilities compared to the old vertex shaders.
The model of programmed tessellation operation differs significantly from other shaders, and can cause confusion when you first get to know it, even if you have experience with vertex and geometric shaders.
Tessellation control shader
In general, the tessellation control shader has access to all vertices of the input patch that have passed through the vertex shader separately. At its input comes the number of vertices in the patch gl_PatchVerticesIn, the sequence number of the patch gl_PrimitiveID and the sequence number of the output vertex gl_InvocationID, about which later. The patch sequence number gl_PrimitiveID is considered to be part of a single glDraw * call. The vertex data itself is accessible via an array of gl_in structures, declared as follows:
in gl_PerVertex { vec4 gl_Position; float gl_PointSize; float gl_ClipDistance[]; } gl_in[gl_MaxPatchVertices]; This array is indexed from zero to gl_PatchVerticesIn - 1. The field of greatest interest in this declaration is the gl_Position field, in which the data from the vertex shader output is written. The number of vertices of the output patch is set in the code of the shader itself by the global declaration:
layout (vertices = 1) out; // and it does not have to match the number of vertices in the input patch. The number of shader calls is equal to the number of output vertices. In each call, the shader has access to all the input nodes of the patch, but it has the right to write only on the gl_InvocationID index of the output array gl_out, which is declared as
out gl_PerVertex { vec4 gl_Position; float gl_PointSize; float gl_ClipDistance[]; } gl_out[]; We now turn to a more interesting fact. The shader can write only on the gl_InvocationID index, but it can read the output array on any index! We remember that the work of shaders is very parallelized, and the order of their call is not determined. This imposes restrictions on data sharing by shaders, but makes SIMD concurrency possible and gives the compiler a blank check to use the most severe optimizations. To prevent these rules from being violated, barrier synchronization is available in the shader of the tessellation control. The call to the built-in function barrier () blocks execution until all the shaders of the patch call this function. Serious restrictions are imposed on the call of this function: it cannot be called from any function except main, it cannot be called in any flow control construct (for, while, switch), and it cannot be called after return.
And finally, the most interesting thing at this stage of the pipeline: the output of the vertices is not the main thing. Polygons will not be collected from coordinates recorded in gl_out. The main product of the tessellation control shader is writing to the following output arrays:
patch out float gl_TessLevelOuter[4]; patch out float gl_TessLevelInner[2]; These arrays control the number of vertices in the so-called abstract patches , which is why this stage is called tessellation control. An abstract patch is a set of points of a two-dimensional geometric shape that is generated at the stage of tessellation primitive generation. Abstract patches are of three types: triangles, squares and isolines. At the same time, for each type of abstract patch, the shader should fill only the gl_TessLevelOuter and gl_TessLevelInner indices it needs, and the remaining indices of these arrays are ignored. The generated patch contains not only the vertices of the geometric figure, but also the coordinates of points on the borders and inside the figure. For example, a square for some values of gl_TessLevelOuter and gl_TessLevelInner will be formed from triangles of this type:

The lower left corner of the square always has the coordinate [0; 0], upper right - [1; 1], and all other points will have corresponding coordinates with values from 0 to 1.
Isolines are essentially square too, divided into rectangles, not triangles. The coordinates of points on isolines will also belong to the interval from 0 to 1.
But the coordinates inside the triangle are arranged in a fundamentally different way: in a two-dimensional triangle, three-component barycentric coordinates are used . Moreover, their values also lie in the interval from 0 to 1, and the triangle is equilateral.
The specific kind of partitioning (which, in fact, is called tessellation in the original sense) of an abstract patch strongly depends on gl_TessLevelOuter and gl_TessLevelInner. We will not dwell on it in detail here, nor will we analyze how Inner differs from Outer. All this is detailed in the relevant section of the OpenGL tutorial.
Now back to our plants. At this stage of the graphics pipeline, we still can not perform any meaningful transformations on the only single point, so the output of this shader will be served with the input vertex unchanged:
gl_out[gl_InvocationID].gl_Position = gl_in[gl_InvocationID].gl_Position; To generate the geometry, we will use a rectangular grid, that is, an abstract patch of the “isoline” type. The contour generation is controlled only by two variables: gl_TessLevelOuter [0] is the number of points along the y coordinate, and gl_TessLevelOuter [1] is the number of points along x . In our program, a cycle of y will run through the stalks of a bush, and for each stem a cycle of x will run along the stem. Therefore, the number of stems (the fourth coordinate of the input point) we write to the corresponding output:
gl_TessLevelOuter[0] = gl_in[gl_InvocationID].gl_Position.w; The number of points along the stem determines the number of segments from which the stem is composed, that is, its detail. In order not to waste resources, let's make the level of detail dependent on the distance between the camera and the bush:
uniform vec3 eyePosition; // . int lod() { // : float dist = distance(gl_in[gl_InvocationID].gl_Position.xyz, eyePosition); // : if(dist < 10.0f) { return 48; } if(dist < 20.0f) { return 24; } if(dist < 80.0f) { return 12; } if(dist < 800.0f) { return 6; } return 4; } On the CPU side, before each glDraw * call, homogeneous variables are populated:
grassShader.setUniformValue("eyePosition", camera.getPosition()); grassShader.setUniformValue("lookDirection", camera.getLookDirection()); The first one is the coordinates of the camera in space, and the second is the direction of gaze. Knowing the position of the camera, the direction of the sight and the coordinate of the bush, we can find out if this bush is behind the camera:

If the bush is in front, then the angle between the direction from the camera forward and from the camera to the bush will be sharp, otherwise - blunt. Accordingly, in the first case the scalar product of the vectors shown in the figure will be greater than zero, and in the second case - less. We calculate the scalar product and use the step function with a step at zero to get a variable that is zero if the bush is behind and one if it is in front:
float halfspaceCull = step(dot(eyePosition - gl_in[gl_InvocationID].gl_Position.xyz, lookDirection), 0); Finally, we can write the number of points for the stems of the future bush:
gl_TessLevelOuter[1] = lod() * halfspaceCull; Shader tessellation
A note about terminology: in English, this shader is called the Tesselation evaluation shader . On the Russian Internet, you can find literal translations like "tessellation evaluation shader" or "tessellation calculation shader". They look awkward and, in my opinion, do not reflect the essence of this shader. Therefore, here the tesselation evaluation shader will be called simply a tessellation shader, unlike the previous stage, where the tessellation control shader was.
Tessellation is enabled only if a tessellation shader is added to the shader program. At the same time, the tessellation control shader is not mandatory: its absence is equivalent to submitting the input patch to the output without changes. The values of the gl_TessLevel * arrays can be set by the CPU by calling glPatchParameterfv with the parameter GL_PATCH_DEFAULT_OUTER_LEVEL or GL_PATCH_DEFAULT_INNER_LEVEL. In this case, all abstract patches in the tessellation shader will be the same. Adding only tessellation shader to the program is meaningless and leads to a shader layout error. The kind of abstract patch, unlike its parameters, is defined in the tessellation shader code:
layout(isolines, equal_spacing) in; // . The tessellation shader is called for each point of the abstract patch. For example, if we ordered isolines with 64x64 dots, then the shader will be called 4096 times. All vertices from the output of the tessellation control shader arrive at its input:
in gl_PerVertex { vec4 gl_Position; float gl_PointSize; float gl_ClipDistance[]; } gl_in[gl_MaxPatchVertices]; gl_PatchVerticesIn, gl_PrimitiveID, gl_TessLevelOuter and gl_TessLevelInner are already familiar to us. The last two variables are of the same type as in the tessellation control shader, but are available only for reading. Finally, the most interesting input variable is
in vec3 gl_TessCoord; It contains the coordinates of the current (for this call) point of the abstract patch. It is declared as vec3, however gl_TessCoord.z only makes sense for triangles. Reading this coordinate for squares or isolines is not defined.
You can submit several variables to the shader output. The main one is vec4 gl_Position, in which you need to record the coordinates of the vertices from which the primitives will be collected for the next stage of the pipeline. In our case, this is a sequence of segments, since shader tessellation makes only the skeleton for the future of the bush.
So, we have many (up to 4096) vertices of the abstract patch, organized into lines that are divided into equal segments. If we draw this shape as lines without changes:
gl_Position = vec4(gl_TessCoord.xy, 0.0f, 1.0f); then we will see something similar to the pictures in the documentation :

Here and below in the screenshots a little side view.
How to make stalks from these lines? To begin, put them vertically:
gl_Position = vec4(gl_TessCoord.yx, 0.0f, 1.0f); 
and learn how to arrange them in a circle, turning around a vertical axis:
vec3 position = vec3(2.0f, gl_TessCoord.x, 0.0f); float alpha = gl_TessCoord.y * 2.0f * M_PI; float cosAlpha = cos(alpha); float sinAlpha = sin(alpha); mat3 circDistribution = mat3( cosAlpha, 0.0f, -sinAlpha, 0.0f, 1.0f, 0.0f, sinAlpha, 0.0f, cosAlpha); position = circDistribution * position; gl_Position = vec4(position, 1.0f); 
However, such lines are more like a fence than a bush. To make our bush more natural, let's twist the line as a cubic Bezier curve:
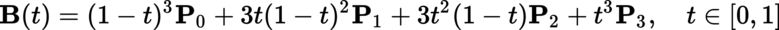
And here the coordinate of gl_TessCoord.x is very useful, about which we agreed to think that it runs along each stem from zero to one. The type of curve completely depends on the reference points P 0 ... P 3 . The bottom of the stem we will always be located on the ground, and its top must look towards the sky, so we take P 0 = (0; 0). And to select at least an approximate position of the remaining free points, the site cubic-bezier.com is perfect , whose sole purpose is to build a curve of the desired type. Now, if gl_TessCoord.x is substituted into the Bezier curve formula, then we get a polyline, the vertices of which lie on the curve, and the segments approximate the curve:
float t = gl_TessCoord.x; // . float t1 = t - 1.0f; // , . // : position.xy = -p0 * (t1 * t1 * t1) + p3 * (t * t * t) + p1 * t * (t1 * t1) * 3.0f - p2 * (t * t) * t1 * 3.0f; // , : position.x += 2.0f; // . , : position.z = 0.0f; 
In the future, we will need to build up polygons around a curved stem, for which each vertex of the broken stem needs to know the plane perpendicular to the stem. From the course of differential geometry it is known that the principal normal vector to the parametric curve can be obtained as a combination of the vector products of the derivatives of the curve with respect to the parameter:
[B ', [B', B '']] (1)
To uniquely define the plane, we need another vector. In our case, the entire curve is located in the vertical plane XY, which means the main normal to is located in it. Therefore, binormal to the curve comes to us for nothing - this is just a constant vector (0; 0; 1). Now we remember that from the cozy XY plane the stem turns around the origin, and therefore the normal plane also needs to be rotated. To do this, it is enough to multiply both of its generators of the vector by the same rotation matrix as the points of the stem. Putting it all together:
// : out vec3 normal; out vec3 binormal; // : normal = normalize( circDistribution * // , . vec3( // , (1): p0.y * (t1 * t1) * -3.0f + p1.y * (t1 * t1) * 3.0f - p2.y * (t * t) * 3.0f + p3.y * (t * t) * 3.0f - p2.y * t * t1 * 6.0f + p1.y * t * t1 * 6.0f, p0.x * (t1 * t1) * 3.0f - p1.x * (t1 * t1) * 3.0f + p2.x * (t * t) * 3.0f - p3.x * (t * t) * 3.0f + p2.x * t * t1 * 6.0f - p1.x * t * t1 * 6.0f, 0.0f )); // : binormal = (circDistribution * vec3(0.0f, 0.0f, 1.0f)); And for clarity, reduce the detail of the stems. Normals are drawn in red and binormals in blue:

Now briefly about the animation. First, the stalks move by themselves. This is done through a circular rotation of the support points of the curve around the other, original points. In this case, the position of the initial points and the initial phase of rotation depend on a random variable (remember the random one-dimensional texture?), Which, in turn, depends on gl_TessCoord.y and gl_PrimitiveID. Thus, each stem in each bush moves in its own way, which creates the illusion of chaos. And since the movement is done through the movement of the control points, the normals and binormals remain completely correct. In fact, we got a skeletal animation, in which the bones are generated on the fly, and do not occupy the memory.
In addition to the bushes' own movement, they are still affected by the “wind”. Wind is the offset of the stem vertices in a user-defined direction by an amount that depends on two user parameters and Perlin noise. At the same time the wind should not shift the roots of the stems, so the offset value is multiplied by the flexibility function:
float flexibility(const in float x) { return x * x; } taken from the coordinate along the stem t1. User wind parameters are called "speed" and "turbulence" purely arbitrary, because changing them in the available user range is similar to changing these air flow parameters. However, this “wind” has nothing to do with real physics. The speed slider in the interface is intentionally limited to a small value, because the wind is applied to the skeleton after the normals have been calculated without adjusting them. Because of this, the normals cease to be so, and with a strong distortion of the skeleton (high "speed" of the wind), self-intersections of polygons appear.
Why Perlin noise, if there is a “noisy” texture? The fact is that the texture values are not a continuous function of the coordinate, unlike the Perlin noise. Therefore, if in each frame we make an offset depending on the noisy texture, we will get a chaotic twitch with a frame rate instead of a smooth wind. High-quality implementation of Perlin’s noise was taken from Stefan Gustavson .
What else is needed to build landfills? First, the stem thickness should decrease from the root to the top. Therefore, we enter the corresponding output variable and transfer to it a thickness depending on the coordinate along the stem:
out float stemThickness; float thickness(const in float x) { return (1.0f - x) / 0.9f; } //... stemThickness = thickness(gl_TessCoord.x); The very coordinate along the stem and the number of the stem in the bush will also be passed down the pipeline:
out float along; flat out float stemIdx; // ... along = gl_TessCoord.x; stemIdx = gl_TessCoord.y; We need them when applying textures.
Geometric Shader
Finally, we come to the completion of the geometric part of our path. At the input of the geometric shader, we get the primitives entirely. If at the entrance of the tessellation stage there were arbitrary patches that could contain a decent amount of data, here the primitives are points, lines, or triangles. , ( , ) glDraw*, , , . , , :
layout(lines) in; in gl_PerVertex { vec4 gl_Position; float gl_PointSize; float gl_ClipDistance[]; } gl_in[]; . :
in vec3 normal[]; in vec3 binormal[]; in float stemThickness[]; in float along[]; flat in float stemIdx[]; , . :
layout(triangle_strip) out; . . , gl_Position. EmitVertex(), . EndPrimitive();
: , , . , .. .
, 5- (flat) :

, :
for(int i = 0; i < numSectors + 1; ++i) { // float around = i / float(numSectors); // , [0; 1] float alpha = (around) * 2.0f * M_PI; // () for(int j = 0; j < 2; ++j) { // // - : vec3 r = cos(alpha) * normal[j] + sin(alpha) * binormal[j]; // : vec3 vertexPosition = r * stemRadius * stemThickness[j] + gl_in[j].gl_Position.xyz; // . // . // , .. gl_Position // , . fragPosition = vertexPosition; // . fragNormal = r; // . fragAlong = along[j]; // . // fragAlong fragAround , // . fragAround = around; // , // . // . stemIdxFrag = stemIdx[j]; // , . // "" , // . gl_Position = viewProjectionMatrix * vec4 (vertexPosition, gl_in[j].gl_Position.w); EmitVertex(); } } EndPrimitive(); , . , . «» , ( ) :
out vec4 outColor; float sfn = float(frameNumber) / totalFrames; float cap(const in float x) { return -abs(fma(x, 2.0f, -1.0f)) + 1.0f; } //... float cell = cellular2x2(vec2(fma(sfn, 100, rand(stemIdxFrag) + fragAlong * 3.0f), cap(fragAround)) * 10.0f).x * 0.3f; outColor = ambient + diffuse + specular + vec4(0.0f, cell, 0.0f, 0.0f) , «» , .
, .
What for?
, ? : , . , - :
- , . , - .
- . - , .
- . .
useful links
. , :
!
UPD1
UPD2
Windows.
Source: https://habr.com/ru/post/314532/
All Articles