Sudoku: so how many of them? Part 2/2
Hi Habr! This is the second part of the translation of an article about counting different sudoku.

In this part, we dive into the theory of groups, starting from the very basics, but affecting only what we need to answer the question: how many really sudoku are there - without any repetitions in the form of turns, reflections, etc. Those who are quite familiar with the theory of groups will probably find little of interesting things here. For the rest, it is very useful to read. Just in case: I do not consider myself a specialist in group theory; when translating an article, I myself essentially studied it almost from scratch. That is, there may well be shoals - write me about them in PM. On the other hand, for the majority of definitions, I climbed to Wikipedia, and I confirmed all the numerical results with my own written program. So, in theory, the number of jambs should tend to zero. But you never know.
')
As usual, my comments are in italics or hidden under spoilers. Under the spoilers you can find the most interesting - pieces of code that verify all the numbers obtained in the narration.
So, in the previous part of the article, we considered that the number of different sudoku grids is equal to N = 6670903752021072936960≈6.671 × 10 21 . But quite often we can get one grid of sudoku from another, using simple transformations. For example, if we have a correctly filled sudoku grid, then turning it 90 °, we get another grid that is different from the original, but still remains correct. In fact, we can consider these grids as identical, because as a result of the transformation, our grid is still one of the Sudoku solutions. Similarly, if we replace all 3-ki in the grid with 4-ki, and all 4-ki with 3-ki, then we will get another correct grid. We could also take some kind of sudoku grid, swap the fifth and sixth lines, and in the end, still get the correct grid. When we make such transformations, we retain such a grid property as its correctness ( In the previous part of the article we did something very similar, but only with a part of the grid — the first strip. Now we are playing with the entire 9 × 9 table. An important difference that now we consider only such transformations that can be applied to any grid (with preservation of correctness), i.e. the previously described operation of swapping the corners of a rectangle inside the grid by sudoku does not fit, since it applies to some grids, and to some - no. ).
Operations of this type are called symmetries. The symmetry of an object is an operation that preserves some property of the object. It is interesting to note that if we apply one symmetry to an object, and immediately after that another symmetry, then the final transformation will be another symmetry. The operation that leaves the object unchanged is also one of the symmetries. For any symmetry, there is another symmetry that rolls back all changes made first. And finally, if we need to apply one symmetry, then the second, and then the third, then we can group either the first and second symmetry together, or the second and third - and eventually get the same transformation.
All these properties tell us that a set of symmetries of an object form a group . A group is a set of G, together with the operation ·, for which the following properties are true:
Note that in the definitions above, we use the multiplicative notation for the group operation. We could use additive notation, in which case the inverse of g would be denoted by -g. ( Multiplicative notation is like our operation “multiply”, and additive operation “add” ).
Exercise Check that the set of integers Z with the operation of addition is a group. For this you need to check the implementation of all four properties.
The group of integers has another very interesting property: the order of addition of numbers is completely unimportant. That is, for any two integers a and b, a + b is the same as b + a. When a group operation satisfies this property (this property is called commutativity ), the group is called abelian .
Let's look at an example of a symmetry group, for example, a square with numbered corners:
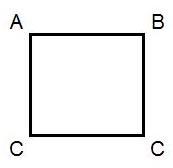
For this geometric object, there are eight transformations that preserve the fact that it is a square. In other words, the square has eight symmetries. All of them are different turns and reflections along with the operation of composition of transformations:
Exercise Select any two transformations from the list above and check that the application of one of them and then the other is also a transformation that is already in this list. Can you find two such transformations that lead to different results depending on the order of their application?
In contrast to the group of integers, the symmetry group of a square is non-Abelian.
The symmetry group G of the correct Sudoku grid contains all the transformations of the square and, in addition, some other transformations such as moving blocks, rows and columns, as well as the composition of all these transformations. Thus, the symmetry group is generated by the following types of transformations:
Important note: this is not a list of all G elements! This is a list of different symmetries of the group, and combining them in all different ways we can get all the other elements of the group. Both the specific transformations of all the types described above, and any composition that differs from these specific “basic” transformations, are all included in the symmetry group G. For example, one of the elements of G is the exchange of the first and second lines, a specific type conversion (5 ). Let X be the set of all valid sudoku grids. We know that this is a set of a finite number of elements. From the fact that each element of G is some correspondence that maps one of the grids to another ( in fact, it maps all grids to some others, that is, it is a certain permutation of all elements from X ), we can conclude that G also includes only a finite number of symmetry elements.
We call two Sudoku grids equivalent , if we can convert one of them to another using one or more symmetries from G. If none of the symmetry sequences converts one of the grids to another, then we call such grids essentially different .
This relation is indeed an equivalence relation in the formal mathematical sense, since it satisfies the following three properties:
For any valid Sudoku grid A, we can consider all grids equivalent to A as really exactly the same as A. If we group together all the grids that are equivalent to each other, then we actually divide the set of all grids into disjoint parts : in fact, X will be divided into such subsets that no two of them have common elements. Mathematicians call such subsets equivalence classes . Any two elements from the same equivalence class are equivalent to each other by some symmetry from G. The set of equivalence classes is denoted as X / G and is read as "X modulo G" or "X mod G" ( also called mathematics X / G factor set ).
In the previous part of the article we wondered about the number of different sudoku nets without any symmetries, and it would be interesting to find the number of significantly different nets. According to the reasoning above, the total number of equivalence classes, or the number of elements in X / G, is nothing more than the number of essentially different sudoku nets. Next, we look at the method that Ed Russell and Frazer Jarvis used in early 2006 to calculate this number.
At first, we’ll draw a little attention to the operation of reassigning numbers and consider only those symmetries that do something with the grid — with the entire grid, with blocks or with individual cells. Consider these symmetries - their types (2) - (6) in the list above - and their compositions. These symmetries give us the group H, in which Russell and Jarvis counted exactly 3359232 different symmetries. In other words, H is a group that is generated by symmetries of types (2) - (6).
Now our notion of equivalence of two grids can be defined as follows: grid A is equivalent to grid B if we can convert grid A by symmetries from group H to some grid C, such that numbers can be reassigned to C so that we finally get grid B. say that A is H-equivalent to C, and C is equivalent to B by remap. Note that H-equivalence and reassignment equivalence are really equivalence relations (they both satisfy three properties from the list above).
We consider that H acts on the set of correct sudoku grids X as follows: each element h from H is a map of X to X, that is, translates each of the grids from X to another (possibly the same) grid from X. In other words, h gives us a way to transform any valid mesh into another valid mesh, and each element h from H gives us such a mapping.
For any symmetry from h from H, we can consider those grids that h leaves in place up to reassignment. We mean all such grids A, that if we apply the symmetry h to A and get the mesh B, then B will be equivalent to A by reassignment ( Such objects are also called fixed points with respect to h ). So we take into account the fact that we did not take into account the reassignment in the symmetry group H.
In order to calculate the number of essentially different sudoku grids, we need a theorem from group theory, called Burnside Lemma.
Burnside Lemma Let G be a finite group that acts on a set X. For each element g of G, let X g denote the set of elements of X that g leaves in place. Then the number of elements in the set X / G is | X / G | = 1 / | G | Σ g in G | X g |, where | - | - the number of elements in the set.
Exercise Imagine a square in which each of the edges is painted in one of two colors - blue or green. Two colorings are essentially the same if there is such a symmetry of the square, which translates the first of these colorings into the second. Use the Burnside Lemma to determine the number of essentially different colorings. (For each of the eight symmetries of a square, count the number of colorings that do not change when applying symmetry. To better understand what is happening, you can draw all 2 4 = 16 colorings of a square and imagine how they transform into each other. Lemma Burnside tells us that to get an answer you need to add the number of unchanging colorings for each symmetry and then divide the resulting sum by the number of symmetries.)
In our case, the finite group H acts on the set X of all possible sudoku correct grids. For each h from H, we want to find the number of such elements of X that they do not change when h is used up to the reassignment of numbers. Then we need to add all these numbers and divide them by the number of elements in H. And in the end we get the answer - the number of significantly different sudoku days. That is, we need to take the arithmetic average of the number of unchanged grids (up to reassignment) for all elements of H.
For example, the following correct sudoku grid is a fixed point to rotate 90 ° clockwise (again, up to reassign numbers):

Exercise Determine how to reassign numbers in a rotated grid above so that it coincides with the original one. Write down all the numbers from 1 to 9 and see where the number 1 goes, then where the number 2 goes, then 3, and so on. In general, make sure that the grid is a fixed point for a given rotation symmetry.
In order to apply the Burnside Lemma (to calculate the number of essentially different grids), we could calculate the number of fixed points for each of 3359232 elements of H. But it turns out that some of these 3359232 transformations have the same number of immutable grids! Russell and Jarvis used the special GAP program and determined that all H elements fall into 275 symmetry classes such that any two symmetries from one class have the same number of unchanging grids, and each symmetry from H has as many fixed points as the element one of these classes ( familiar process, isn't it? ). Therefore, we just need to count the number of fixed points for only one symmetry from each of the 275 classes. Knowing how many symmetries are in each of the classes, we can then find out the mean, as in the Burnside Lemma.
Exercise Consider the reflection of the grid sudoku relative to the horizontal axis passing through the center of the grid, I mean through the fifth row. Note that the fifth line after the reflection will remain unchanged. Can you reassign numbers in the reflected grid so that it coincides with the original? And what about fixed points to reflect on the horizontal axis? Is there a grid in general that does not change? (Recall the fact that we are now considering some kind of correct Sudoku grid, and in the fifth line are all nine numbers).
As can be seen from the exercise above, in H there are such symmetries for which there are no fixed points. Russell and Jarvis were surprised to find that in fact, as many as 248 classes out of 275 contain symmetries for which there is not a single fixed point. So they need only calculate the number of unchanged grids for symmetries from the 27 remaining classes and find how many symmetries are contained in each of these classes before using the Burnside Lemma. They wrote a program that makes the last calculations and as a result got the number 5472730538≈5.473 × 10 9 - the number of significantly different sudoku grids.
2, 4×4, , , ( ).
, 4×4, — 9×9 — . 4!, 4! .
, 1 2 , 3 4 — . 4! , 3 4, . , , 3 4 , . , 3 , 4 — .
1 3 , 2 4 . , 4!×2×2 . , , — , , 2 , 4 — . :
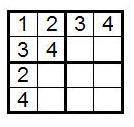
2, 3, (3,3) 1, 4.
, (3,3) 1, .
, (3,3) 4. , , — 4, (4,4) 1, 2 3. , 4!×2×2, , 3 (4,4) ( ). , 4×4 4!×2×2×3=288.
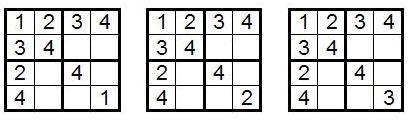
. , — ( ?) 2 3.
, , 4×4.
. , , , , . 3 17 , , . 3 — ( , ).
, ?
( , ): , ? , n, , n 2 -1 . n n 2 -2 , , , . , 3, 3 2 -1=8 , . ( ? ).
, , : n , n 2 -1 . , , n n 2 -1 , . , A B, B A. .
2 2 2 -1=3 . .
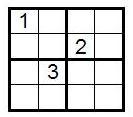
4×4, () , .
, , 3, , n — . n n+1 ( ), , , . , n NP- . NP-, :
NP- — , , . , , .
, . ( ) . , .
.
, .

In this part, we dive into the theory of groups, starting from the very basics, but affecting only what we need to answer the question: how many really sudoku are there - without any repetitions in the form of turns, reflections, etc. Those who are quite familiar with the theory of groups will probably find little of interesting things here. For the rest, it is very useful to read. Just in case: I do not consider myself a specialist in group theory; when translating an article, I myself essentially studied it almost from scratch. That is, there may well be shoals - write me about them in PM. On the other hand, for the majority of definitions, I climbed to Wikipedia, and I confirmed all the numerical results with my own written program. So, in theory, the number of jambs should tend to zero. But you never know.
')
As usual, my comments are in italics or hidden under spoilers. Under the spoilers you can find the most interesting - pieces of code that verify all the numbers obtained in the narration.
Symmetry
So, in the previous part of the article, we considered that the number of different sudoku grids is equal to N = 6670903752021072936960≈6.671 × 10 21 . But quite often we can get one grid of sudoku from another, using simple transformations. For example, if we have a correctly filled sudoku grid, then turning it 90 °, we get another grid that is different from the original, but still remains correct. In fact, we can consider these grids as identical, because as a result of the transformation, our grid is still one of the Sudoku solutions. Similarly, if we replace all 3-ki in the grid with 4-ki, and all 4-ki with 3-ki, then we will get another correct grid. We could also take some kind of sudoku grid, swap the fifth and sixth lines, and in the end, still get the correct grid. When we make such transformations, we retain such a grid property as its correctness ( In the previous part of the article we did something very similar, but only with a part of the grid — the first strip. Now we are playing with the entire 9 × 9 table. An important difference that now we consider only such transformations that can be applied to any grid (with preservation of correctness), i.e. the previously described operation of swapping the corners of a rectangle inside the grid by sudoku does not fit, since it applies to some grids, and to some - no. ).
Operations of this type are called symmetries. The symmetry of an object is an operation that preserves some property of the object. It is interesting to note that if we apply one symmetry to an object, and immediately after that another symmetry, then the final transformation will be another symmetry. The operation that leaves the object unchanged is also one of the symmetries. For any symmetry, there is another symmetry that rolls back all changes made first. And finally, if we need to apply one symmetry, then the second, and then the third, then we can group either the first and second symmetry together, or the second and third - and eventually get the same transformation.
All these properties tell us that a set of symmetries of an object form a group . A group is a set of G, together with the operation ·, for which the following properties are true:
- If g and h are elements of G, then g · h is also an element of G (Mathematicians say that G is closed with respect to the operation ·).
- If g, h and k are elements of G, then g · (h · k) = (g · h) · k (This property of the group operation is called associativity ).
- There is an element e in G such that g · e = e · g = g for all g from G (This element e is called the neutral element of G, since it leaves each element of G unchanged with respect to the operation).
- For each element g of G, there is another element h of G such that g · h = h · g = e, where e is a neutral element (the element h is called the inverse of g, denoted as g -1 ).
Note that in the definitions above, we use the multiplicative notation for the group operation. We could use additive notation, in which case the inverse of g would be denoted by -g. ( Multiplicative notation is like our operation “multiply”, and additive operation “add” ).
Exercise Check that the set of integers Z with the operation of addition is a group. For this you need to check the implementation of all four properties.
The group of integers has another very interesting property: the order of addition of numbers is completely unimportant. That is, for any two integers a and b, a + b is the same as b + a. When a group operation satisfies this property (this property is called commutativity ), the group is called abelian .
Let's look at an example of a symmetry group, for example, a square with numbered corners:
For this geometric object, there are eight transformations that preserve the fact that it is a square. In other words, the square has eight symmetries. All of them are different turns and reflections along with the operation of composition of transformations:
- Rotate 0 degrees (neutral).
- Rotate clockwise 90 degrees.
- Rotate clockwise 180 degrees.
- Rotate clockwise 270 degrees.
- The reflection about the horizontal axis (which passes through the center of the square).
- The reflection about the vertical axis (which also passes through the center of the square).
- The reflection is diagonal from the lower left to the upper right.
- The reflection on the diagonal from the upper left corner to the lower right.
Exercise Select any two transformations from the list above and check that the application of one of them and then the other is also a transformation that is already in this list. Can you find two such transformations that lead to different results depending on the order of their application?
In contrast to the group of integers, the symmetry group of a square is non-Abelian.
The symmetry group G of the correct Sudoku grid contains all the transformations of the square and, in addition, some other transformations such as moving blocks, rows and columns, as well as the composition of all these transformations. Thus, the symmetry group is generated by the following types of transformations:
- Reassign nine digits.
- Shuffle three stacks.
- Permutation of three lanes.
- Permutation of three columns in a stack.
- Permutations of three lines in a strip.
- Any reflections and turns (from the symmetry list of the square).
Important note: this is not a list of all G elements! This is a list of different symmetries of the group, and combining them in all different ways we can get all the other elements of the group. Both the specific transformations of all the types described above, and any composition that differs from these specific “basic” transformations, are all included in the symmetry group G. For example, one of the elements of G is the exchange of the first and second lines, a specific type conversion (5 ). Let X be the set of all valid sudoku grids. We know that this is a set of a finite number of elements. From the fact that each element of G is some correspondence that maps one of the grids to another ( in fact, it maps all grids to some others, that is, it is a certain permutation of all elements from X ), we can conclude that G also includes only a finite number of symmetry elements.
We call two Sudoku grids equivalent , if we can convert one of them to another using one or more symmetries from G. If none of the symmetry sequences converts one of the grids to another, then we call such grids essentially different .
This relation is indeed an equivalence relation in the formal mathematical sense, since it satisfies the following three properties:
- The grid A is equivalent to itself (this property is called reflexivity ).
- If A is equivalent to B, then B is equivalent to A (this property is called symmetry ).
- If A is equivalent to B, and B is equivalent to C, then A is equivalent to C (this property is called transitivity ).
For any valid Sudoku grid A, we can consider all grids equivalent to A as really exactly the same as A. If we group together all the grids that are equivalent to each other, then we actually divide the set of all grids into disjoint parts : in fact, X will be divided into such subsets that no two of them have common elements. Mathematicians call such subsets equivalence classes . Any two elements from the same equivalence class are equivalent to each other by some symmetry from G. The set of equivalence classes is denoted as X / G and is read as "X modulo G" or "X mod G" ( also called mathematics X / G factor set ).
In the previous part of the article we wondered about the number of different sudoku nets without any symmetries, and it would be interesting to find the number of significantly different nets. According to the reasoning above, the total number of equivalence classes, or the number of elements in X / G, is nothing more than the number of essentially different sudoku nets. Next, we look at the method that Ed Russell and Frazer Jarvis used in early 2006 to calculate this number.
At first, we’ll draw a little attention to the operation of reassigning numbers and consider only those symmetries that do something with the grid — with the entire grid, with blocks or with individual cells. Consider these symmetries - their types (2) - (6) in the list above - and their compositions. These symmetries give us the group H, in which Russell and Jarvis counted exactly 3359232 different symmetries. In other words, H is a group that is generated by symmetries of types (2) - (6).
Comment
In any incomprehensible situation, start to make meth to write code. And now it is completely incomprehensible where the number 3359232 comes from. Therefore, let's start writing code to check that the group H has exactly 3359232 different symmetries.
We begin with a structure that describes the symmetry of a group. By the Cayley theorem , every finite group is isomorphic to a subgroup of some symmetric group. If we speak in an understandable language, then any finite group can be represented as some system of permutations. So for the group H, we use a permutation of length 81 — one permutation element per sudoku cell.
Those. in each position of the 9x9 table, we store the position number to which the element will move at the current position after applying symmetry. Please note - symmetry knows nothing about what numbers are in sudoku now. The above code spells out the creation of symmetries such as the neutral element, rearrangement of the stacks, rearrangement of the columns, and rotation of 90 degrees.
Exercise Show that all symmetries of types (2) - (6) can be obtained by composition of those symmetries that we implemented in the code.
Next in the code is the implementation of the composition or multiplication of symmetries. At the end, we added the implementation of finding the inverse element (we do not need it yet, but we will need it later).
Now, based on the existing symmetries, let's generate the whole group H:
Operators for comparing and determining which element is less needed purely so that set can correctly perform its operations (otherwise it will even refuse to compile). Next, we implement a bypass of the symmetry group H using a wide bypass (one could also use a depth to depth, but it eats up too much memory on the recursion stack).
In more detail: first we put neutral symmetry in the Q queue. After that, we extract and process symmetries until they are in the queue. The processing goes like this: we just extract the symmetry from the queue and multiply it by all the “basic” symmetries available to us. The Set set plays the role of an array of flags and stores all the symmetries obtained by the current moment. If after multiplication we get a new symmetry - such that it is not in Set - then we memorize it in the Set and put Q at the end of the queue. If, after multiplication, we find that the new symmetry is already in Set, we don’t We do, as we have already processed this symmetry earlier.
As a result, at the end of the execution of the algorithm, all symmetries from the group H will accumulate in Set (in general, strictly speaking, all permutations of a certain group P, which is isomorphic to the group H, will accumulate there, but we will not zadvodstvu about this now). Running the code confirms that there are exactly 3359232 elements in H.
By the way, in the SYMMETRY structure for each permutation element, it is not for nothing that the unsigned char type is chosen. In the calculation process, we store millions of objects in the Set and in the Q queue (which weigh 80 bytes each), so you need to be prepared for the program to consume about 450MB of memory during the calculation and about 300MB at the end when the queue becomes empty .
We begin with a structure that describes the symmetry of a group. By the Cayley theorem , every finite group is isomorphic to a subgroup of some symmetric group. If we speak in an understandable language, then any finite group can be represented as some system of permutations. So for the group H, we use a permutation of length 81 — one permutation element per sudoku cell.
struct SYMMETRY { unsigned char m[9][9]; void print() { for (int i=0; i<9; i++) { for (int j=0; j<9; j++) printf( "%2d ", (int)m[i][j] ); printf( "\n" ); } printf( "\n" ); } static SYMMETRY E() { SYMMETRY re; unsigned char t = 0; for (int i=0; i<9; i++) for (int j=0; j<9; j++) re.m[i][j] = t++; return re; } static SYMMETRY swap_stacks( int i, int j ) { SYMMETRY re = SYMMETRY::E(); for (int a=0; a<9; a++) for (int b=0; b<3; b++) swap( re.m[a][i*3+b], re.m[a][j*3+b] ); return re; } static SYMMETRY swap_columns( int s, int i, int j ) { SYMMETRY re = SYMMETRY::E(); for (int a=0; a<9; a++) swap( re.m[a][s*3+i], re.m[a][s*3+j] ); return re; } static SYMMETRY rotate() { SYMMETRY re = SYMMETRY::E(); for (int a=0; a<5; a++) for (int b=0; b<4; b++) { unsigned char tmp = re.m[a][b]; re.m[a][b] = re.m[8-b][a]; re.m[8-b][a] = re.m[8-a][8-b]; re.m[8-a][8-b] = re.m[b][8-a]; re.m[b][8-a] = tmp; } return re; } SYMMETRY multiply( SYMMETRY g ) { SYMMETRY re; for (int i=0; i<9; i++) for (int j=0; j<9; j++) re.m[i][j] = gm[m[i][j]/9][m[i][j]%9]; return re; } SYMMETRY inverse() { SYMMETRY re; for (int i=0; i<9; i++) for (int j=0; j<9; j++) re.m[m[i][j]/9][m[i][j]%9] = i*9+j; return re; } }; Those. in each position of the 9x9 table, we store the position number to which the element will move at the current position after applying symmetry. Please note - symmetry knows nothing about what numbers are in sudoku now. The above code spells out the creation of symmetries such as the neutral element, rearrangement of the stacks, rearrangement of the columns, and rotation of 90 degrees.
Exercise Show that all symmetries of types (2) - (6) can be obtained by composition of those symmetries that we implemented in the code.
Next in the code is the implementation of the composition or multiplication of symmetries. At the end, we added the implementation of finding the inverse element (we do not need it yet, but we will need it later).
Now, based on the existing symmetries, let's generate the whole group H:
bool operator== (const SYMMETRY & A, const SYMMETRY & B) { for (int a=0; a<9; a++) for (int b=0; b<9; b++) if (Am[a][b] != Bm[a][b]) return false; return true; } bool operator< (const SYMMETRY & A, const SYMMETRY & B) { for (int a=0; a<9; a++) for (int b=0; b<9; b++) if (Am[a][b] != Bm[a][b]) return Am[a][b] < Bm[a][b]; return false; } set< SYMMETRY > Set; queue< SYMMETRY > Q; void bfs_push( SYMMETRY G ) { if (Set.find( G ) != Set.end()) return; Set.insert( G ); Q.push( G ); if (Set.size()%100000==0) fprintf( stderr, "G.sz=%d\n", (int)Set.size() ); } void find_all_elements_of_group() { Q.push( SYMMETRY::E() ); Set.insert( SYMMETRY::E() ); while (Q.size()>0) { SYMMETRY G = Q.front(); Q.pop(); bfs_push( G.multiply( SYMMETRY::rotate() ) ); for (int i=0; i<3; i++) for (int j=i+1; j<3; j++) { bfs_push( G.multiply( SYMMETRY::swap_stacks(i,j) ) ); for (int k=0; k<3; k++) bfs_push( G.multiply( SYMMETRY::swap_columns(k,i,j) ) ); } } printf( "sudoku group size %d\n", (int)Set.size() ); fprintf( stderr, "sudoku group size %d\n", (int)Set.size() ); } Operators for comparing and determining which element is less needed purely so that set can correctly perform its operations (otherwise it will even refuse to compile). Next, we implement a bypass of the symmetry group H using a wide bypass (one could also use a depth to depth, but it eats up too much memory on the recursion stack).
In more detail: first we put neutral symmetry in the Q queue. After that, we extract and process symmetries until they are in the queue. The processing goes like this: we just extract the symmetry from the queue and multiply it by all the “basic” symmetries available to us. The Set set plays the role of an array of flags and stores all the symmetries obtained by the current moment. If after multiplication we get a new symmetry - such that it is not in Set - then we memorize it in the Set and put Q at the end of the queue. If, after multiplication, we find that the new symmetry is already in Set, we don’t We do, as we have already processed this symmetry earlier.
As a result, at the end of the execution of the algorithm, all symmetries from the group H will accumulate in Set (in general, strictly speaking, all permutations of a certain group P, which is isomorphic to the group H, will accumulate there, but we will not zadvodstvu about this now). Running the code confirms that there are exactly 3359232 elements in H.
By the way, in the SYMMETRY structure for each permutation element, it is not for nothing that the unsigned char type is chosen. In the calculation process, we store millions of objects in the Set and in the Q queue (which weigh 80 bytes each), so you need to be prepared for the program to consume about 450MB of memory during the calculation and about 300MB at the end when the queue becomes empty .
Comment
By the way, how can one imagine in the form of a permutation group a group that is generated by symmetries of all types (1) - (6)? Permutations - they are stupid, they do not look at what numbers are written in sudoku. They stupidly mix elements without delving into the essence.
In order to take into account symmetries of type (1), we transform the sudoku grid slightly. Namely: translate it into 3D (no matter how strange it sounds). Imagine a 9x9x9 cube, onto which our sudoku grid is projected from above. That is, for each cell of Sudoku there is a column of 9 single cubes in a large cube. Well, now for each column we do the following: if the number i is in the corresponding cell of the sudoku, then we paint the i-th (counting from above) cube of the column black and all the other cubes - white. As a result, we get a cube, each of 729 cubes of which is painted in one of two colors (black or white), with exactly one cube painted in black in each column. Well, now all symmetries of types (2) - (6) are mixing of the columns of a cube, while symmetries of type (1) are mixing of horizontal layers of this cube.
Voila - we expressed the symmetry group generated by symmetries of types (1) - (6) through the subgroup of the permutation group of order 729.
In order to take into account symmetries of type (1), we transform the sudoku grid slightly. Namely: translate it into 3D (no matter how strange it sounds). Imagine a 9x9x9 cube, onto which our sudoku grid is projected from above. That is, for each cell of Sudoku there is a column of 9 single cubes in a large cube. Well, now for each column we do the following: if the number i is in the corresponding cell of the sudoku, then we paint the i-th (counting from above) cube of the column black and all the other cubes - white. As a result, we get a cube, each of 729 cubes of which is painted in one of two colors (black or white), with exactly one cube painted in black in each column. Well, now all symmetries of types (2) - (6) are mixing of the columns of a cube, while symmetries of type (1) are mixing of horizontal layers of this cube.
Voila - we expressed the symmetry group generated by symmetries of types (1) - (6) through the subgroup of the permutation group of order 729.
Now our notion of equivalence of two grids can be defined as follows: grid A is equivalent to grid B if we can convert grid A by symmetries from group H to some grid C, such that numbers can be reassigned to C so that we finally get grid B. say that A is H-equivalent to C, and C is equivalent to B by remap. Note that H-equivalence and reassignment equivalence are really equivalence relations (they both satisfy three properties from the list above).
We consider that H acts on the set of correct sudoku grids X as follows: each element h from H is a map of X to X, that is, translates each of the grids from X to another (possibly the same) grid from X. In other words, h gives us a way to transform any valid mesh into another valid mesh, and each element h from H gives us such a mapping.
For any symmetry from h from H, we can consider those grids that h leaves in place up to reassignment. We mean all such grids A, that if we apply the symmetry h to A and get the mesh B, then B will be equivalent to A by reassignment ( Such objects are also called fixed points with respect to h ). So we take into account the fact that we did not take into account the reassignment in the symmetry group H.
Comment
For a better understanding of the essence of the expression “up to reassignment”, one should accept the fact that sometimes the set of objects on which we apply all symmetries can, after applying symmetries, be additionally self-twisting to some normal form.
Another way to improve understanding is: instead of the set X of all sudoku grids, it is better to consider the set Y — the set of all equivalence classes of X with respect to equivalence by redirection. Those. each element in Y is a set of 9! sudoku grids that go into each other when reassigning numbers (in general, I imagine each of these elements as a transparent sphere in which 9 separate sudoku paper grids float). And when we apply to element y from Y element h from H - we transform at once all the grids of sudoku inside y in accordance with the symmetry h. And as a result we get a new set of grids y '(and the sets, as you know, are compared without taking into account the order of the elements in them).
It should be noted that self-twisting does not contradict the Cayley theorem — it is for the group itself, and not for the set that we are trying to act on with this group. We can act as a group on very different sets: even on sets of one or two elements, even on another group. The main thing is that the set on which we act satisfies a small list of properties .
Another way to improve understanding is: instead of the set X of all sudoku grids, it is better to consider the set Y — the set of all equivalence classes of X with respect to equivalence by redirection. Those. each element in Y is a set of 9! sudoku grids that go into each other when reassigning numbers (in general, I imagine each of these elements as a transparent sphere in which 9 separate sudoku paper grids float). And when we apply to element y from Y element h from H - we transform at once all the grids of sudoku inside y in accordance with the symmetry h. And as a result we get a new set of grids y '(and the sets, as you know, are compared without taking into account the order of the elements in them).
It should be noted that self-twisting does not contradict the Cayley theorem — it is for the group itself, and not for the set that we are trying to act on with this group. We can act as a group on very different sets: even on sets of one or two elements, even on another group. The main thing is that the set on which we act satisfies a small list of properties .
In order to calculate the number of essentially different sudoku grids, we need a theorem from group theory, called Burnside Lemma.
Burnside Lemma Let G be a finite group that acts on a set X. For each element g of G, let X g denote the set of elements of X that g leaves in place. Then the number of elements in the set X / G is | X / G | = 1 / | G | Σ g in G | X g |, where | - | - the number of elements in the set.
Exercise Imagine a square in which each of the edges is painted in one of two colors - blue or green. Two colorings are essentially the same if there is such a symmetry of the square, which translates the first of these colorings into the second. Use the Burnside Lemma to determine the number of essentially different colorings. (For each of the eight symmetries of a square, count the number of colorings that do not change when applying symmetry. To better understand what is happening, you can draw all 2 4 = 16 colorings of a square and imagine how they transform into each other. Lemma Burnside tells us that to get an answer you need to add the number of unchanging colorings for each symmetry and then divide the resulting sum by the number of symmetries.)
In our case, the finite group H acts on the set X of all possible sudoku correct grids. For each h from H, we want to find the number of such elements of X that they do not change when h is used up to the reassignment of numbers. Then we need to add all these numbers and divide them by the number of elements in H. And in the end we get the answer - the number of significantly different sudoku days. That is, we need to take the arithmetic average of the number of unchanged grids (up to reassignment) for all elements of H.
For example, the following correct sudoku grid is a fixed point to rotate 90 ° clockwise (again, up to reassign numbers):
Exercise Determine how to reassign numbers in a rotated grid above so that it coincides with the original one. Write down all the numbers from 1 to 9 and see where the number 1 goes, then where the number 2 goes, then 3, and so on. In general, make sure that the grid is a fixed point for a given rotation symmetry.
In order to apply the Burnside Lemma (to calculate the number of essentially different grids), we could calculate the number of fixed points for each of 3359232 elements of H. But it turns out that some of these 3359232 transformations have the same number of immutable grids! Russell and Jarvis used the special GAP program and determined that all H elements fall into 275 symmetry classes such that any two symmetries from one class have the same number of unchanging grids, and each symmetry from H has as many fixed points as the element one of these classes ( familiar process, isn't it? ). Therefore, we just need to count the number of fixed points for only one symmetry from each of the 275 classes. Knowing how many symmetries are in each of the classes, we can then find out the mean, as in the Burnside Lemma.
Comment
From the paragraph above it is not at all clear how Russell and Jarvis received 275 classes. And in general, what kind of classes in general? But, if you delve into their original article (and not the scientific publication that you are translating), you can understand that we are talking about contingency classes .
Information from Wikipedia : the elements g 1 and g 2 of the group G are called conjugate if there exists an element h from G for which h · g 1 · h -1 = g 2 .
Exercise Show that the relation is a equivalence relation (three properties from the definition of equivalence in the text above will help you).
Exercise Show that if two elements g 1 and g 2 of a group G are conjugate (with h · g 1 · h -1 = g 2 for some h from H), then they have the same number of fixed points. Note: show that for any fixed point x from X for g 1 the object y = x · h -1 (also from X) is the fixed point for g 2 , and for each fixed point y from X for g 2 the object x = y · H of X is a fixed point for g 1 . As a result, a bijection is constructed between the fixed points of both symmetries.
So, with the theory figured out, now we need to deal with the practice. And with her not so simple. We, in fact, need for each element g from H to iterate over another element h from H, and then build a connection between g and h · g · h -1 . And at the end, look at the connected components. Only here the order of group H is under 3 million and we will build ties to the forehead until the end of the centuries (well, at least until the end of this year for sure). Therefore, we will act smarter.
To begin with, let us take not all symmetries as h, but only a very small subset of them. For example, the set of symmetries, from which we in one of the past spoilers generate the group H. As a result, all elements of H will be grouped into partial equivalence classes, they will become much smaller, and we will already join them in an amicable way.
The associative array classes stores a representative of each class, as well as the number of elements in each class. Set2 is an array of flags, like Set, which we use for the needs of the current iteration, and at the very end we clear it. The classes are generated as follows: first, all the “base” symmetries are added to the ops array, after which, starting from the element that has not yet been considered, we recursively walk along the conjugacy graph using depth traversal and construct the conjugacy class. After that we take the next not yet considered symmetry, find the class for it, and so on.
This code (together with the previous one) already consumes at the peak of the order of 900MB of memory, of which about 256MB falls on the recursion stack (it could again be implemented as a width walk, but in this case the depth walk was not so voracious from memory so bearable). And ... as a result of execution we get the desired 275 classes.
Luck? We have not yet processed our result. Actually, we don’t need to process anything and we really got the right partition into classes (this could have been proved before launch). The arguments about the correctness of our algorithm are approximately as follows:
Consider some conjugate symmetries g 1 and g 2 , then there is a symmetry h, for which g 2 = h · g 1 · h -1 . At the same time, h can be represented as a composition of symmetries, say h = a · b · c, where a, b, c are some kind of “base” symmetry. Then g 2 = h · g 1 · h -1 = (a · b · c) · g 1 · (a · b · c) -1 = a · b · c · g 1 · c -1 · b -1 · A -1 = (a · (b · (c · g 1 · c -1 ) · b -1 ) · a -1 ). That is, from the symmetry of g 1, in our algorithm we would go to the symmetry p 1 = c · g 1 · c -1 , from p 1 to p 2 = b · g 1 · b -1 , and from p 2 - to a · g 1 · a -1 = g 2 . From here we get that the algorithm is correct.
Information from Wikipedia : the elements g 1 and g 2 of the group G are called conjugate if there exists an element h from G for which h · g 1 · h -1 = g 2 .
Exercise Show that the relation is a equivalence relation (three properties from the definition of equivalence in the text above will help you).
Exercise Show that if two elements g 1 and g 2 of a group G are conjugate (with h · g 1 · h -1 = g 2 for some h from H), then they have the same number of fixed points. Note: show that for any fixed point x from X for g 1 the object y = x · h -1 (also from X) is the fixed point for g 2 , and for each fixed point y from X for g 2 the object x = y · H of X is a fixed point for g 1 . As a result, a bijection is constructed between the fixed points of both symmetries.
So, with the theory figured out, now we need to deal with the practice. And with her not so simple. We, in fact, need for each element g from H to iterate over another element h from H, and then build a connection between g and h · g · h -1 . And at the end, look at the connected components. Only here the order of group H is under 3 million and we will build ties to the forehead until the end of the centuries (well, at least until the end of this year for sure). Therefore, we will act smarter.
To begin with, let us take not all symmetries as h, but only a very small subset of them. For example, the set of symmetries, from which we in one of the past spoilers generate the group H. As a result, all elements of H will be grouped into partial equivalence classes, they will become much smaller, and we will already join them in an amicable way.
map< SYMMETRY, int > classes; SYMMETRY cur_g; set< SYMMETRY > Set2; void dfs1( SYMMETRY g, vector< SYMMETRY > & ops ) { if (Set2.find( g ) != Set2.end()) return; Set2.insert( g ); classes[cur_g]++; for (int i=0; i<(int)ops.size(); i++) dfs1( ops[i].multiply(g).multiply( ops[i].inverse() ), ops ); } void find_conjugacy_classes() { vector< SYMMETRY > ops; ops.push_back( SYMMETRY::rotate() ); for (int i=0; i<3; i++) for (int j=i+1; j<3; j++) { ops.push_back( SYMMETRY::swap_stacks(i,j) ); for (int k=0; k<3; k++) ops.push_back( SYMMETRY::swap_columns(k,i,j) ); } int ind = 0; for (set< SYMMETRY >::iterator it = Set.begin(); it != Set.end(); it++) if (Set2.find( *it ) == Set2.end()) { cur_g = *it; dfs1( *it, ops ); printf( "M[%d]=%d\n", ind, classes[cur_g] ); fprintf( stderr, "M[%d]=%d\n", ind, classes[cur_g] ); ind++; } Set2.clear(); printf( "number of classes after step 1 %d\n", (int)classes.size() ); fprintf( stderr, "number of classes after step 1 %d\n", (int)classes.size() ); } The associative array classes stores a representative of each class, as well as the number of elements in each class. Set2 is an array of flags, like Set, which we use for the needs of the current iteration, and at the very end we clear it. The classes are generated as follows: first, all the “base” symmetries are added to the ops array, after which, starting from the element that has not yet been considered, we recursively walk along the conjugacy graph using depth traversal and construct the conjugacy class. After that we take the next not yet considered symmetry, find the class for it, and so on.
This code (together with the previous one) already consumes at the peak of the order of 900MB of memory, of which about 256MB falls on the recursion stack (it could again be implemented as a width walk, but in this case the depth walk was not so voracious from memory so bearable). And ... as a result of execution we get the desired 275 classes.
Luck? We have not yet processed our result. Actually, we don’t need to process anything and we really got the right partition into classes (this could have been proved before launch). The arguments about the correctness of our algorithm are approximately as follows:
Consider some conjugate symmetries g 1 and g 2 , then there is a symmetry h, for which g 2 = h · g 1 · h -1 . At the same time, h can be represented as a composition of symmetries, say h = a · b · c, where a, b, c are some kind of “base” symmetry. Then g 2 = h · g 1 · h -1 = (a · b · c) · g 1 · (a · b · c) -1 = a · b · c · g 1 · c -1 · b -1 · A -1 = (a · (b · (c · g 1 · c -1 ) · b -1 ) · a -1 ). That is, from the symmetry of g 1, in our algorithm we would go to the symmetry p 1 = c · g 1 · c -1 , from p 1 to p 2 = b · g 1 · b -1 , and from p 2 - to a · g 1 · a -1 = g 2 . From here we get that the algorithm is correct.
Exercise Consider the reflection of the grid sudoku relative to the horizontal axis passing through the center of the grid, I mean through the fifth row. Note that the fifth line after the reflection will remain unchanged. Can you reassign numbers in the reflected grid so that it coincides with the original? And what about fixed points to reflect on the horizontal axis? Is there a grid in general that does not change? (Recall the fact that we are now considering some kind of correct Sudoku grid, and in the fifth line are all nine numbers).
As can be seen from the exercise above, in H there are such symmetries for which there are no fixed points. Russell and Jarvis were surprised to find that in fact, as many as 248 classes out of 275 contain symmetries for which there is not a single fixed point. So they need only calculate the number of unchanged grids for symmetries from the 27 remaining classes and find how many symmetries are contained in each of these classes before using the Burnside Lemma. They wrote a program that makes the last calculations and as a result got the number 5472730538≈5.473 × 10 9 - the number of significantly different sudoku grids.
Comment
We are approaching the most complex part of the code - the code for counting the number of fixed points for each of the 275 symmetry classes. And the fact that we consider objects equivalent in reassignment of numbers — a sort of generalized completely filled sudoku grid — introduces much complexity. There are 6670903752021072936960/9 in total! = 18383222420692992 (this is the same number of all sudoku grids divided by the number of variants that are obtained by reassigning numbers). Denote the set of such generalized grids as Y.
So, the subtask for the solution: we need for some symmetry g to count the number of fixed points from the set Y (there are 275 such subtasks in total). What happens to each fixed point when g is applied? The numbers in the sudoku grid are swapped according to some permutation, then the numbers are reassigned, and after that we get the original grid. And the fact that the numbers are somehow reassigned makes it difficult to build a search. However, note that if some grid is a fixed point for any one reassignment, then for all other reassignments it is not a fixed point. Therefore, we can sort out all possible reassignments, find the number of fixed points for each of them, and then add everything up.
It turns out now we need to solve this sub-task: given the symmetry g and the reassignment of numbers h, we need to calculate for them the number of fixed points from Y. Now consider some fixed point y from Y, and specifically - the number p in some cell (i, j). When applying g to y, (i, j) goes to a certain position (i ', j') = (i, j) · g, in which, according to the reassignment h, will be the number q = p · h. Since the final grid is equal to the initial grid, the number q must be in the initial grid at position (i ', j').
That is, the following happens. g is some permutation of the Sudoku grid cells, which can be divided into cycles. , 90 , (1,1)->(1,9)->(9,9)->(9,1)->(1,1) 4. h — , 9 . . , 2->3->2 2. , (1,1) 2, (1,9) 3, (9,9) — 2, (9,1) — 3. . , — , « ».
, ( , ).
, , ( - ):
init() , . , init() . next_perm() . clear() T, .
, :
set_num() , — . unset_num() . , set_num() unset_num() , «» , , .
, , , , , . What kind? . , - : , . - , , — , , . : - , .
:
, is_immovable() , «» , has_bad_cycle() — .
, , :
process_class() . — . . — . - . . dfs2().
50 . ( , 0), :
, . .
.
So, the subtask for the solution: we need for some symmetry g to count the number of fixed points from the set Y (there are 275 such subtasks in total). What happens to each fixed point when g is applied? The numbers in the sudoku grid are swapped according to some permutation, then the numbers are reassigned, and after that we get the original grid. And the fact that the numbers are somehow reassigned makes it difficult to build a search. However, note that if some grid is a fixed point for any one reassignment, then for all other reassignments it is not a fixed point. Therefore, we can sort out all possible reassignments, find the number of fixed points for each of them, and then add everything up.
It turns out now we need to solve this sub-task: given the symmetry g and the reassignment of numbers h, we need to calculate for them the number of fixed points from Y. Now consider some fixed point y from Y, and specifically - the number p in some cell (i, j). When applying g to y, (i, j) goes to a certain position (i ', j') = (i, j) · g, in which, according to the reassignment h, will be the number q = p · h. Since the final grid is equal to the initial grid, the number q must be in the initial grid at position (i ', j').
That is, the following happens. g is some permutation of the Sudoku grid cells, which can be divided into cycles. , 90 , (1,1)->(1,9)->(9,9)->(9,1)->(1,1) 4. h — , 9 . . , 2->3->2 2. , (1,1) 2, (1,9) 3, (9,9) — 2, (9,1) — 3. . , — , « ».
, ( , ).
, , ( - ):
struct MEGAGRID { int T[9][9]; bool R[9][10], C[9][10], B[9][10]; int S[9][9]; // symmetry permutation int s_cycle[9][9]; // length of cycle for every element int M[10]; // mapping permutation int m_cycle[10]; // length of cycle for every element void init( SYMMETRY sym ) { for (int a=0; a<9; a++) for (int b=0; b<9; b++) S[a][b] = sym.m[a][b]; memset( s_cycle, 0, sizeof( s_cycle ) ); for (int a=0; a<9; a++) for (int b=0; b<9; b++) if (s_cycle[a][b] == 0) { int cycle_len = 0; int i = a, j = b; while(1) { int tmp = S[i][j]; i = tmp/9; j = tmp%9; cycle_len++; if (i==a && j==b) break; } while(1) { s_cycle[i][j] = cycle_len; int tmp = S[i][j]; i = tmp/9; j = tmp%9; if (i==a && j==b) break; } } for (int a=1; a<10; a++) M[a] = a; for (int a=1; a<10; a++) m_cycle[a] = 1; } bool next_perm() { if (!next_permutation( M+1, M+10 )) return false; memset( m_cycle, 0, sizeof( m_cycle ) ); for (int a=1; a<=9; a++) if (m_cycle[a] == 0) { int cycle_len = 0; int i = a; while(1) { i = M[i]; cycle_len++; if (i==a) break; } while(1) { m_cycle[i] = cycle_len; i = M[i]; if (i==a) break; } } return true; } void clear() { memset( T, 0, sizeof( T ) ); memset( R, 0, sizeof( R ) ); memset( C, 0, sizeof( C ) ); memset( B, 0, sizeof( B ) ); } } G; init() , . , init() . next_perm() . clear() T, .
, :
struct MEGAGRID { /* old code */ bool set_num( int num, int x, int y ) { int n0=num, x0=x, y0=y; if (s_cycle[x][y] % m_cycle[num] != 0) return false; int L = s_cycle[x][y]; for (int a=0; a<L; a++) { if (R[x][num] || C[y][num] || B[(x/3)*3+(y/3)][num]) { if (a>0) unset_num( n0, x0, y0, a ); // undo changes return false; } T[x][y] = num; R[x][num] = true; C[y][num] = true; B[(x/3)*3+(y/3)][num] = true; int tmp = S[x][y]; x = tmp/9; y = tmp%9; num = M[num]; } return true; } void unset_num( int num, int x, int y, int sz=0 ) { int L = s_cycle[x][y]; if (sz!=0) L = sz; for (int a=0; a<L; a++) { T[x][y] = 0; R[x][num] = false; C[y][num] = false; B[(x/3)*3+(y/3)][num] = false; int tmp = S[x][y]; x = tmp/9; y = tmp%9; num = M[num]; } } } G; set_num() , — . unset_num() . , set_num() unset_num() , «» , , .
, , , , , . What kind? . , - : , . - , , — , , . : - , .
:
struct MEGAGRID { /* old code */ bool is_immovable() { for (int a=0; a<9; a++) { bool flag = true; for (int b=0; b<9; b++) if (S[a][b] != a*9+b) flag = false; if (flag) return true; } for (int b=0; b<9; b++) { bool flag = true; for (int a=0; a<9; a++) if (S[a][b] != a*9+b) flag = false; if (flag) return true; } for (int a=0; a<3; a++) for (int b=0; b<3; b++) { bool flag = true; for (int i=0; i<3; i++) for (int j=0; j<3; j++) if (S[a*3+i][b*3+j] != (a*3+i)*9+b*3+j) flag = false; if (flag) return true; } return false; } bool has_bad_cycle() { for (int a=0; a<9; a++) for (int b=0; b<9; b++) { int x = S[a][b]/9, y = S[a][b]%9; if (!(x==a && y==b)) if (x==a || y==b || (x/3)*3+(y/3)==(a/3)*3+(b/3)) return true; } return false; } } G; , is_immovable() , «» , has_bad_cycle() — .
, , :
long long sudoku_count; void dfs2( int x, int y ) { while(1) // find next empty cell { y++; if (y==9) { y=0; x++; } if (x==9) // no empty cell { sudoku_count++; return; } if (GT[x][y]==0) break; } for (int a=1; a<=9; a++) if (G.set_num( a, x, y )) { dfs2( x, y ); G.unset_num( a, x, y ); } } long long process_class( SYMMETRY s ) { if (s==SYMMETRY::E()) return 18383222420692992L; long long re = 0; G.init( s ); bool imm = G.is_immovable(); bool hbc = G.has_bad_cycle(); if (imm && hbc) return re; if (hbc) G.next_perm(); int ind = 0; do { ind++; if (ind%1000==0) fprintf( stderr, "." ); G.clear(); bool flag = true; for (int a=1; a<=9; a++) { int x = (a-1)/3, y = (a-1)%3; if (GT[x][y]>0 && GT[x][y]!=a) { flag = false; break; } if (GT[x][y]==0 && !G.set_num( a, x, y )) { flag = false; break; } } if (flag) { sudoku_count = 0; dfs2( 0, 0 ); re += sudoku_count; } if (imm) break; } while (G.next_perm()); return re; } void process_all_classes() { long long answer = 0; long long sum = 0; int i = 0; for (map< SYMMETRY, int >::iterator it = classes.begin(); it != classes.end(); it++) { fprintf( stderr, "class %3d", i ); long long tmp = process_class( it->first ); printf( "class %3d %6d x %17lld\n", i, it->second, tmp ); fprintf( stderr, " %6d x %17lld\n", it->second, tmp ); i++; answer += tmp * it->second; sum += it->second; } printf( "total sum %lld\n", answer ); printf( "essentialy different sudoku grids %lld\n", answer/sum ); } process_class() . — . . — . - . . dfs2().
50 . ( , 0), :
number of classes 275 class 0 1 x 18383222420692992 class 78 972 x 449445888 class 114 2916 x 155492352 class 120 1296 x 30258432 class 132 69984 x 13056 class 135 16 x 107495424 class 137 96 x 21233664 class 140 192 x 4204224 class 189 3888 x 27648 class 195 10368 x 1854 class 199 144 x 14837760 class 201 864 x 2085120 class 204 1728 x 294912 class 220 7776 x 13824 class 222 15552 x 1728 class 229 288 x 5184 class 231 1728 x 2592 class 234 3456 x 1296 class 244 93312 x 288 class 247 64 x 2508084 class 257 1152 x 6342480 class 262 15552 x 3456 class 264 31104 x 6480 class 265 2304 x 648 class 269 5184 x 323928 class 271 20736 x 288 class 274 20736 x 162 total sum 18384171550626816 essentialy different sudoku grids 5472730538 total time 3013 sec , . .
.
4x4
2, 4×4, , , ( ).
, 4×4, — 9×9 — . 4!, 4! .
, 1 2 , 3 4 — . 4! , 3 4, . , , 3 4 , . , 3 , 4 — .
1 3 , 2 4 . , 4!×2×2 . , , — , , 2 , 4 — . :
2, 3, (3,3) 1, 4.
, (3,3) 1, .
, (3,3) 4. , , — 4, (4,4) 1, 2 3. , 4!×2×2, , 3 (4,4) ( ). , 4×4 4!×2×2×3=288.
. , — ( ?) 2 3.
, , 4×4.
Some more interesting facts.
. , , , , . 3 17 , , . 3 — ( , ).
, ?
( , ): , ? , n, , n 2 -1 . n n 2 -2 , , , . , 3, 3 2 -1=8 , . ( ? ).
, , : n , n 2 -1 . , , n n 2 -1 , . , A B, B A. .
2 2 2 -1=3 . .
4×4, () , .
, , 3, , n — . n n+1 ( ), , , . , n NP- . NP-, :
- , .. .
- , , (1).
NP- — , , . , , .
Instead of conclusion
, . ( ) . , .
.
, .
Source: https://habr.com/ru/post/314514/
All Articles