Pigeons brutalize Monty Hall's paradox better than people.

Pigeons give people a head start in solving Monty Hall's dilemmas, which could allow them to successfully perform on the talk show of the same name. This pattern can, in turn, shed light on why it is so difficult for people.

What is remarkable about this dilemma? With seeming simplicity, it confuses the logical chains of our conclusions, forcing people (but not pigeons), literally, to wander in three pines, or rather, in the doorway. This is typical of representatives of very different cultural traditions: Americans, Chinese, Swedes and Brazilians make the same wrong choice.

The cognitive psychologist Massimo Piattelli-Palmarini remarked on this point : Not a single statistical task is even close by the ability to fool all people at all times .

In this article we will find out what the dilemma is, find the theoretical correct solution, check it in R, tell you about the intellectual battle between people and pigeons and find out its results.

Monty Hall's Dilemma

Monty Hall’s so-called dilemma is a well-known enigma, named after the first TV host on the American TV show “Offer a Deal”, in which he gave participants a choice of three doors, one of which was a car, and the other two were goats. The prize and the goats were pre-arranged randomly and did not further change their locations. After the participant made his choice, the presenter always opened one of the remaining two doors, behind which, as he knew ahead, there was no prize. Then the player was offered the opportunity to change his choice or leave everything as it is .

There are actually several possible Monty strategies .

• Hellish Monty : the lead offers to change if the door is right.
• Angelic Monty : the presenter offers to change if the door is wrong.
• The moderator chooses one of the goats and opens it if the player chooses another door.

The lead strategy has become a classic when the player opens the goat-door with any initial choice of the player and offers to change his choice or leave everything as it is. From it we will continue to make a start.

The vast majority of players, respondents and subjects refused to change their choice , despite the fact that it doubled their chances of winning. At the same time, people think that in the remaining two doors the chances of winning are equal and there is no point in changing their choice. If you think the same way, do not be embarrassed, because you are not mistaken.

When a columnist, Marilin vos Savant ^[1], published the decision in Parade Magazine , she simply had a flurry of letters from readers expressing their disagreement. Here, for example such.

I am sure that soon you will receive many letters from students of high schools and colleges. Perhaps you should keep these addresses, they will help you in future releases.
W. Robert Smith, Ph.D. / Georgia State University

I’m shocked that even after at least three mathematicians have corrected you, you still don’t see your mistake.
Kent Ford / Dickinson State University

You are a goat yourself.
Glenn Calkins / Western State College

Total - about 10 thousand letters. As you can see, trolling flourished even in those times when for this it was necessary to spend much more time and effort than now, and also pay for a postal envelope and a postage stamp.

The talented Hungarian mathematician Paul Erdős also fell for the trick and refused to even make a decision until he saw with his own eyes a computer simulation of the experimental results. Honestly, it is hard to believe in it, but the rumor went, nevertheless.

Exposing

The most concise explanation of the DMH solution (Monti Hall Dilemmas) is given in a pie chart.

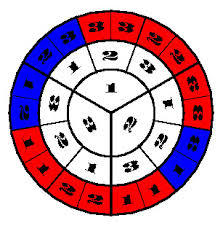
, — , . — . , 1/3, 2/3.

, .

• — , 1- .
• — , 2- .

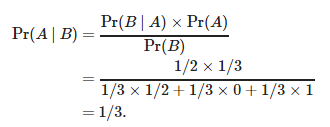
Pr(A) — 3 , 1/3. , Pr(B|A)=1/2.
Pr(B), , . , :

1. 1, 2.
2. 1- , 1/2 2.
3. 2- , 3, .
4. 3- , 2, .

, 1/3, . , , , 2/3.

?

, Julia Schroder Walter Hebranson , - .

. , , — .

. . , , . , , - . — , . . .

30 36.33% 96.33%.

: — . — . — .

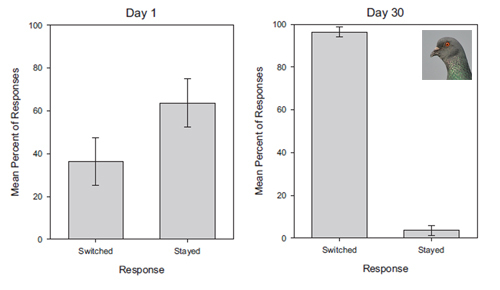
. 30 , .

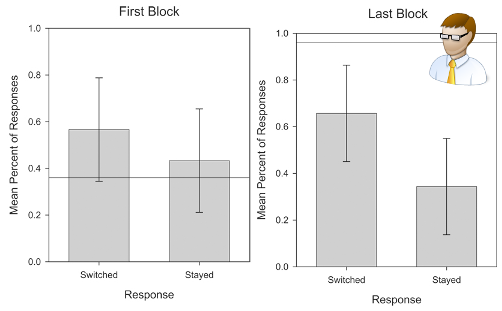
56.67% 65.67%. , .

, , . . , .

. . 30.17% , 15- — 4.33%. home sapiens : 30%, — 27.67%.

?

. , . . . . , , , .

: , , . , .

. , , , R. .

5:543)$ R -f monty.r

 Monty Hall Problem Simulation
"  "

                            = 3380 
                 = 10000 
       = 0.338 
      = 0.3333333 

" "

                            = 6620 
                 = 10000 
       = 0.662 
     = 0.6666667> 
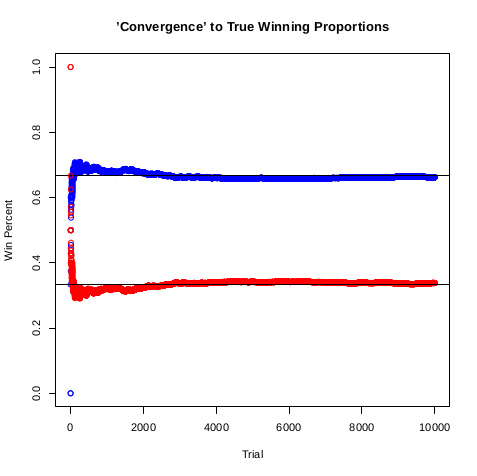
> ## Plot 'convergence' to true winning proportions
> ## Blue is switching doors, red is staying
> plot.new()
> plot(cumsum(changewin) / c(1:N), main = "'Convergence' to True Winning Proportions",
+      xlab = "Trial", ylab = "Win Percent", ylim = c(0, 1), col = "blue")
> abline(h = 2/3)
> points(cumsum(staywin) / c(1:N), type = "p", col = "red")
> abline(h = 1/3)

1/3 2/3.

1. Are Birds Smarter Than Mathematicians? Pigeons (Columba livia) Perform Optimally on a Version of the Monty Hall Dilemma
2. Pigeons Beat Humans at Solving 'Monty Hall' Problem
3. Pigeons outperform humans at the Monty Hall Dilemma
4. Monty Hall Problem: Intuitive and Mathematical Solutions

1. ↑ Ask Merilin, IQ.