Procedural generation of planetary maps
It's about cartography, dealing with fantastic worlds.
At the moment, procedural card generation is already an extensive topic that has been developed mainly in the game industry. There are ways to automatically generate various types of maps from simple images in role-playing and action games to tile maps in strategic games. The first ones give an idea of the game's location and are characterized by a small coverage of the territory, the second ones can simulate vast areas of entire planets, but have little detail.
Methods of creating maps and reliefs for small areas are well known for a long time:
middle shift method, noise function method (Noise Functions) . Relatively recently, an interesting method appeared based on polygon splitting of a plane by polygons Polygonal Map Generation for Games . There is a site where links to various resources on the artificial generation of reliefs are collected.
As a rule, more often than not, the case is limited to creating textures for modeling the landscape, but no matter how beautiful and spectacular the landscape is, it is not yet a complete map.
')
In general, we will further distinguish the relief from the map: we consider relief as a kind of texture and have the opportunity to observe it, unlike relief, we can “touch” the map, this means that map objects must be independent entities and there is a certain way in which they can be changed . In addition, the presence of the map does not cancel the existence and observation of the relief.
There are many software tools and standards for working with maps of the Earth. Geographic information systems are designed to capture, manipulate, analyze and present all types of geographic data. OpenStreetMap (OSM) is one of the examples of GIS, which is designed to collect geographic data and give it to the public.
A wide range of various GIS, as well as many software tools and techniques that have emerged as a result of the development of the project OpenStreetMap, simply suggests to be used to work with maps of fantastic planets. If such already existed as the Earth exists with its surface.
Next, I describe the proposed method of generating the planet (on the fingers). Making the planetary scale of relief rather quickly comes to the limits of the computing system. The number of calculations performed increases quadratically with respect to the reduction of the step between the grid points on the sphere. This is the main reason why planetary maps were not created. The second of the reasons is the need to implement a global river network and link it with relief.
Getting to this task, the first desire that arises is to avoid calculating trigonometric functions, but on the sphere this is not possible. There is a way when, to create a texture on a sphere, it is first drawn on the faces of a regular polyhedron, such as a cube, and then displayed on the sphere. It is clear that the angles of the polyhedron with this display should give distortion. Applying such a method to a large planet would cause too much distortion. We will use another variation of this approach.
Without discontinuities, we map the planet's sphere onto the circular cones connected at the base, the line of the equator, at the same time, must coincide with the line of connecting the cones . At the end of the process of building relief on cones do the inverse mapping on the sphere. Of course, distortions cannot be avoided, but by making mappings in different ways, it is possible to distribute the resulting distortions on the sphere in different ways. The good news is that we completely eliminate the calculation of trigonometric functions.
As a working display, we use the variant at which distances along the meridians are preserved. Vertically, we avoid distortion at all, and horizontally, distortion grows linearly, and near the poles, the growth of distortion decreases, reaching a maximum of 1.57.
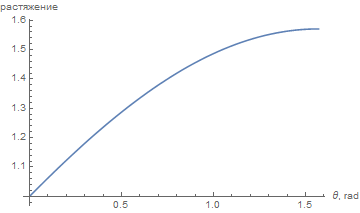
This mapping is well suited to planets that have oceans or white spots near the poles. At the equator or in the middle latitudes, it is difficult to visually notice the introduced distortions (the distortions introduced by the selected main grid may be more noticeable).
Even taking into account simplification using a conic projection, calculations for the entire planet remain costly in terms of memory consumption. To solve this problem, we resort to two-level generation. At first we generate the main or global grid of heights. The main parameter of this grid is the value of gn, which determines the number of grid divisions by a quarter of the equator to be 2 gn . The process of generating heights on the main grid reveals the main areas of land. It also establishes the sea level by the ratio of the number of points falling into the land and ocean.
With examples of planets that were made, gn = 7. This is a rather modest value and, in the process of optimizing algorithms and building up hardware, it will be possible to gradually increase gn for new planets.
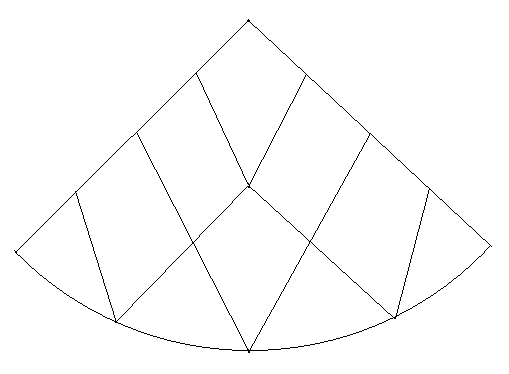
The process of building the main grid. We divide the equator of 4 * 2 gn points into identical segments of length l, then retreat along the zero meridian distance l to the north and divide the parallel on which we are located by 4 * (2 gn -1) segments. We continue the process further to the pole, reducing at each iteration the number of points on each next parallel by 4. We do the same with the southern hemisphere. Each point of the global grid defines a rhombus on a cone (exceptions: points of poles that have no comparable rhombus) and the entire double cone is divided into rhombuses. Note that these are rhombuses on the surface of a circular cone, and not on a plane. The following figure shows a fragment of the main grid of rhombuses, containing a quarter of the upper cone for gn = 2 (without a claim to accuracy, but useful for understanding the essence of the matter).
The transition to the grid on double cones leads to an unexpected result: the points of the main grid (without poles) are assembled into an array of 2 gn by 4 * 2 gn . To do this, first enter the points of the southern cone and equator into the array, and then place the points of the northern cone to the right of the free places, turning them from left to right. As a result, many algorithms in the implementation on cones look simpler than their possible analogues on the sphere.
Here, for example, how the code of a function that increases the height of a neighborhood of the south pole of radius r by one may look simple (the real function in the project code looks different, taking into account the more general case).
When generating relief on the main grid, we strive to ensure that several significant land areas are formed. Achieving the separation of land into separate areas is important for parallelization of calculations, since the river system is built for each land area independently. This is a model of the planet depicting the distribution of the heights of the main grid.

To go to the next level, we set a local grid in each diamond and build a relief starting from the already known heights at the tops of the diamond (which belong to the main grid). Thus, the final relief will be a kind of multi-fractal.
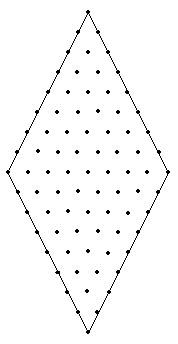
The main parameter of the local grid is the ln value, which specifies the number of grid steps in two directions: 2 ln +1 and 2 * 2 ln +1, respectively. In the figure, an example of a rhombus with a local grid with ln = 3.
To generate a relief, you can implement an algorithm in which only the array of the heights of one rhombus is in memory . This allows the generation of planets with high resolution of map objects.
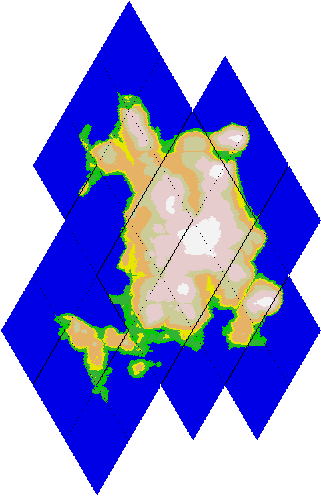
When implementing projects with complex and multi-step algorithms, there is often a need to build visual images of intermediate data. Here, for example, the image of an average island size in the process of creating a planet; dividing into rhombuses by a dotted line is visible.
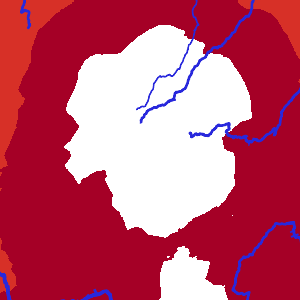
There is a work dedicated to the creation of the river system. But the two-level nature of generation required to create specific algorithms for the components of the river from individual pieces. Schematic representation of the rivers for a small island, see the figure. The final image of the rivers will depend on their depth in the mouth.
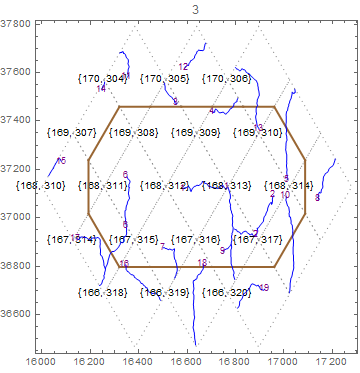
Lakes arise as places of local minima in the main grid of heights. The task is to determine the polygon inside which this local minimum is contained.
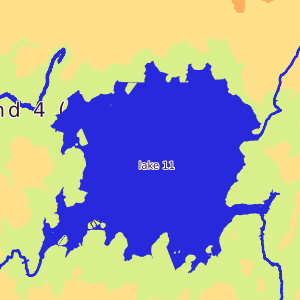
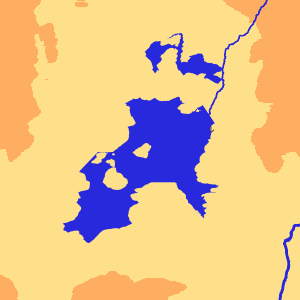
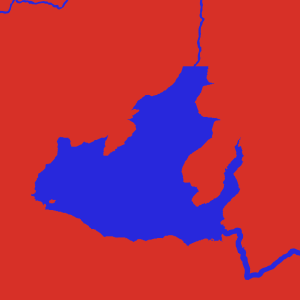
Several beautiful fragments of maps of non-existent worlds, which arise as a result of the implementation of the described algorithm.


Status of procedural card generation
At the moment, procedural card generation is already an extensive topic that has been developed mainly in the game industry. There are ways to automatically generate various types of maps from simple images in role-playing and action games to tile maps in strategic games. The first ones give an idea of the game's location and are characterized by a small coverage of the territory, the second ones can simulate vast areas of entire planets, but have little detail.
Methods of creating maps and reliefs for small areas are well known for a long time:
middle shift method, noise function method (Noise Functions) . Relatively recently, an interesting method appeared based on polygon splitting of a plane by polygons Polygonal Map Generation for Games . There is a site where links to various resources on the artificial generation of reliefs are collected.
As a rule, more often than not, the case is limited to creating textures for modeling the landscape, but no matter how beautiful and spectacular the landscape is, it is not yet a complete map.
')
In general, we will further distinguish the relief from the map: we consider relief as a kind of texture and have the opportunity to observe it, unlike relief, we can “touch” the map, this means that map objects must be independent entities and there is a certain way in which they can be changed . In addition, the presence of the map does not cancel the existence and observation of the relief.
GIS and OpenStreetMap as a way to present fantastic maps
There are many software tools and standards for working with maps of the Earth. Geographic information systems are designed to capture, manipulate, analyze and present all types of geographic data. OpenStreetMap (OSM) is one of the examples of GIS, which is designed to collect geographic data and give it to the public.
A wide range of various GIS, as well as many software tools and techniques that have emerged as a result of the development of the project OpenStreetMap, simply suggests to be used to work with maps of fantastic planets. If such already existed as the Earth exists with its surface.
Procedural generation of the planet
Next, I describe the proposed method of generating the planet (on the fingers). Making the planetary scale of relief rather quickly comes to the limits of the computing system. The number of calculations performed increases quadratically with respect to the reduction of the step between the grid points on the sphere. This is the main reason why planetary maps were not created. The second of the reasons is the need to implement a global river network and link it with relief.
Double cone as a sphere approximation
Getting to this task, the first desire that arises is to avoid calculating trigonometric functions, but on the sphere this is not possible. There is a way when, to create a texture on a sphere, it is first drawn on the faces of a regular polyhedron, such as a cube, and then displayed on the sphere. It is clear that the angles of the polyhedron with this display should give distortion. Applying such a method to a large planet would cause too much distortion. We will use another variation of this approach.
Without discontinuities, we map the planet's sphere onto the circular cones connected at the base, the line of the equator, at the same time, must coincide with the line of connecting the cones . At the end of the process of building relief on cones do the inverse mapping on the sphere. Of course, distortions cannot be avoided, but by making mappings in different ways, it is possible to distribute the resulting distortions on the sphere in different ways. The good news is that we completely eliminate the calculation of trigonometric functions.
As a working display, we use the variant at which distances along the meridians are preserved. Vertically, we avoid distortion at all, and horizontally, distortion grows linearly, and near the poles, the growth of distortion decreases, reaching a maximum of 1.57.

This mapping is well suited to planets that have oceans or white spots near the poles. At the equator or in the middle latitudes, it is difficult to visually notice the introduced distortions (the distortions introduced by the selected main grid may be more noticeable).
Two levels of card generation
Even taking into account simplification using a conic projection, calculations for the entire planet remain costly in terms of memory consumption. To solve this problem, we resort to two-level generation. At first we generate the main or global grid of heights. The main parameter of this grid is the value of gn, which determines the number of grid divisions by a quarter of the equator to be 2 gn . The process of generating heights on the main grid reveals the main areas of land. It also establishes the sea level by the ratio of the number of points falling into the land and ocean.
With examples of planets that were made, gn = 7. This is a rather modest value and, in the process of optimizing algorithms and building up hardware, it will be possible to gradually increase gn for new planets.
The process of building the main grid. We divide the equator of 4 * 2 gn points into identical segments of length l, then retreat along the zero meridian distance l to the north and divide the parallel on which we are located by 4 * (2 gn -1) segments. We continue the process further to the pole, reducing at each iteration the number of points on each next parallel by 4. We do the same with the southern hemisphere. Each point of the global grid defines a rhombus on a cone (exceptions: points of poles that have no comparable rhombus) and the entire double cone is divided into rhombuses. Note that these are rhombuses on the surface of a circular cone, and not on a plane. The following figure shows a fragment of the main grid of rhombuses, containing a quarter of the upper cone for gn = 2 (without a claim to accuracy, but useful for understanding the essence of the matter).

The transition to the grid on double cones leads to an unexpected result: the points of the main grid (without poles) are assembled into an array of 2 gn by 4 * 2 gn . To do this, first enter the points of the southern cone and equator into the array, and then place the points of the northern cone to the right of the free places, turning them from left to right. As a result, many algorithms in the implementation on cones look simpler than their possible analogues on the sphere.
Here, for example, how the code of a function that increases the height of a neighborhood of the south pole of radius r by one may look simple (the real function in the project code looks different, taking into account the more general case).
import Data.Array.Base import Data.Array.ST type Height = Int type GHeights = UArray (Int,Int) Height type GHeightsMutable s = (STUArray s (Int,Int) Height) -- | Make Heights array mutable thawGHeightsArr :: GHeights -> ST s (GHeightsMutable s) thawGHeightsArr = unsafeThaw -- | Increase values around south pole shiftSouth :: GHeights -> Int -> GHeights shiftSouth hs r = runSTUArray $ do a <- thawGHeightsArr hs mapM_ (\y -> (mapM_ (\x -> do v <- readArray a (x,y) writeArray a (x,y) (v + 1) ) [1..4*y]) ) [1..r] return a When generating relief on the main grid, we strive to ensure that several significant land areas are formed. Achieving the separation of land into separate areas is important for parallelization of calculations, since the river system is built for each land area independently. This is a model of the planet depicting the distribution of the heights of the main grid.

To go to the next level, we set a local grid in each diamond and build a relief starting from the already known heights at the tops of the diamond (which belong to the main grid). Thus, the final relief will be a kind of multi-fractal.
The main parameter of the local grid is the ln value, which specifies the number of grid steps in two directions: 2 ln +1 and 2 * 2 ln +1, respectively. In the figure, an example of a rhombus with a local grid with ln = 3.

To generate a relief, you can implement an algorithm in which only the array of the heights of one rhombus is in memory . This allows the generation of planets with high resolution of map objects.
When implementing projects with complex and multi-step algorithms, there is often a need to build visual images of intermediate data. Here, for example, the image of an average island size in the process of creating a planet; dividing into rhombuses by a dotted line is visible.

Rivers and lakes
There is a work dedicated to the creation of the river system. But the two-level nature of generation required to create specific algorithms for the components of the river from individual pieces. Schematic representation of the rivers for a small island, see the figure. The final image of the rivers will depend on their depth in the mouth.

Lakes arise as places of local minima in the main grid of heights. The task is to determine the polygon inside which this local minimum is contained.
Poetry cards
Several beautiful fragments of maps of non-existent worlds, which arise as a result of the implementation of the described algorithm.






Source: https://habr.com/ru/post/313420/
All Articles