Divide & Conquer over the Strassen algorithm

Hello friends! As students of a well-known educational project, we, with bo_0m , after our introductory lecture on the Advanced programming course in Java , received our first homework. It was necessary to implement a program that would multiply the matrices. And everything would be okay, so it was a coincidence that next week the Joker conference was supposed to take place, and our teacher decided to cancel the lesson on this occasion, giving us a few hours of free Friday evening. Do not waste the same time in vain! Since no one is in a hurry, then you can get creative.

Welcome, under the hood ↓

The first thing that comes to mind

Probably every technical university student had to multiply the matrices. The algorithm was always the same, namely, a simple cubic method of multiplication. And no matter how it sounds, but this method is not so bad (for matrix dimensions less than 100).
')
We all started with this:

for (int i = 0; i < A.rows(); i++) { for (int j = 0; j < B.columns(); j++) { for (int k = 0; k < A.columns(); k++) { C[i][j] += A[i][k] * B[k][j]; } } } 

Looking ahead, I will say that we will use a modified version using transposition. About this modification is well written here , and not only about it.

Okay, let's go further!

Strassen Algorithm

Perhaps not everyone knows, but the author of the algorithm, Volker Strassen, is not only alive, but also actively teaching, as well as an honorary professor in the department of mathematics and statistics at the University of Constance. Be sure to read about this person at least on the wiki .
A bit of theory from Wikipedia:

Let A and B be two (n * n) -matrices, moreover, n is a power of 2. Then each A and B matrix can be divided into four ((n / 2) * (n / 2)) - matrices and through them be expressed product of matrices A and B:

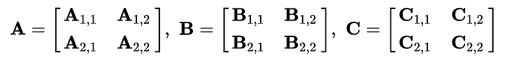
Define new items:

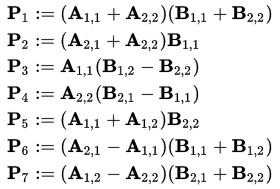
Thus, we need only 7 multiplications at each stage of the recursion. The elements of the matrix C are expressed from Pk by the formulas:

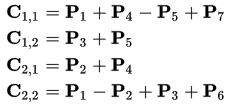
The recursive process continues n times, until the size of the matrices Ci, j is sufficiently small, then the usual method of matrix multiplication is used. This is done due to the fact that the Strassen algorithm loses its efficiency in comparison with the ordinary one on small matrices due to the greater number of additions.

let's go to practice!

To implement the Strassen algorithm, we need additional functions. As mentioned above, the algorithm works only with square matrices, the dimension of which is equal to degree 2, so we will bring the original matrices to this form.

For this, a function was implemented that defines a new dimension:

 private static int log2(int x) { int result = 1; while ((x >>= 1) != 0) result++; return result; } //****************************************************************************************** private static int getNewDimension(int[][] a, int[][] b) { return 1 << log2(Collections.max(Arrays.asList(a.length, a[0].length, b[0].length))); //  -  } 

And a function that expands the matrix to the desired size:

 private static int[][] addition2SquareMatrix(int[][] a, int n) { int[][] result = new int[n][n]; for (int i = 0; i < a.length; i++) { for (int j = 0; j < a[i].length; j++) { result[i][j] = a[i][j]; } } return result; } 

The original matrices now satisfy the requirements for the implementation of the Strassen algorithm. We also need a function that allows us to split the matrix of size n * n into four matrices (n / 2) * (n / 2) and the inverse to reconstruct the matrix:

 private static void splitMatrix(int[][] a, int[][] a11, int[][] a12, int[][] a21, int[][] a22) { int n = a.length >> 1; for (int i = 0; i < n; i++) { System.arraycopy(a[i], 0, a11[i], 0, n); System.arraycopy(a[i], n, a12[i], 0, n); System.arraycopy(a[i + n], 0, a21[i], 0, n); System.arraycopy(a[i + n], n, a22[i], 0, n); } } //****************************************************************************************** private static int[][] collectMatrix(int[][] a11, int[][] a12, int[][] a21, int[][] a22) { int n = a11.length; int[][] a = new int[n << 1][n << 1]; for (int i = 0; i < n; i++) { System.arraycopy(a11[i], 0, a[i], 0, n); System.arraycopy(a12[i], 0, a[i], n, n); System.arraycopy(a22[i], 0, a[i + n], n, n); } return a; } 

So we got to the most interesting, the main function of matrix multiplication by the Strassen algorithm is as follows:


At this could be finished. The implemented algorithm works homework done , but inquiring minds crave adult perfomance. Let Java 7 be with us.

It's time to parallelize

Java 7 provides an excellent API for parallelizing recursive tasks. With its release, one of the additions to the java.util.concurrent packages appeared - the implementation of the Divide and Conquer - Fork-Join paradigm. The idea is this: recursively we divide the task into subtasks, solve, and then combine the results. More information about this technology can be found in the documentation .

Let's see how easily and effectively you can apply this paradigm to our Strassen algorithm.

Climax

You probably can’t wait to see the performance comparison of the algorithms on real hardware. Immediately make a reservation that we will conduct testing on square matrices. So, we have:

1. Traditional (Cubic) Matrix Multiplication Method
2. Traditional using transpose
3. Strassen Algorithm
4. Strassen's Parallel Algorithm

The dimension of the matrices will be set in the interval [100..4000] and in increments of 100.



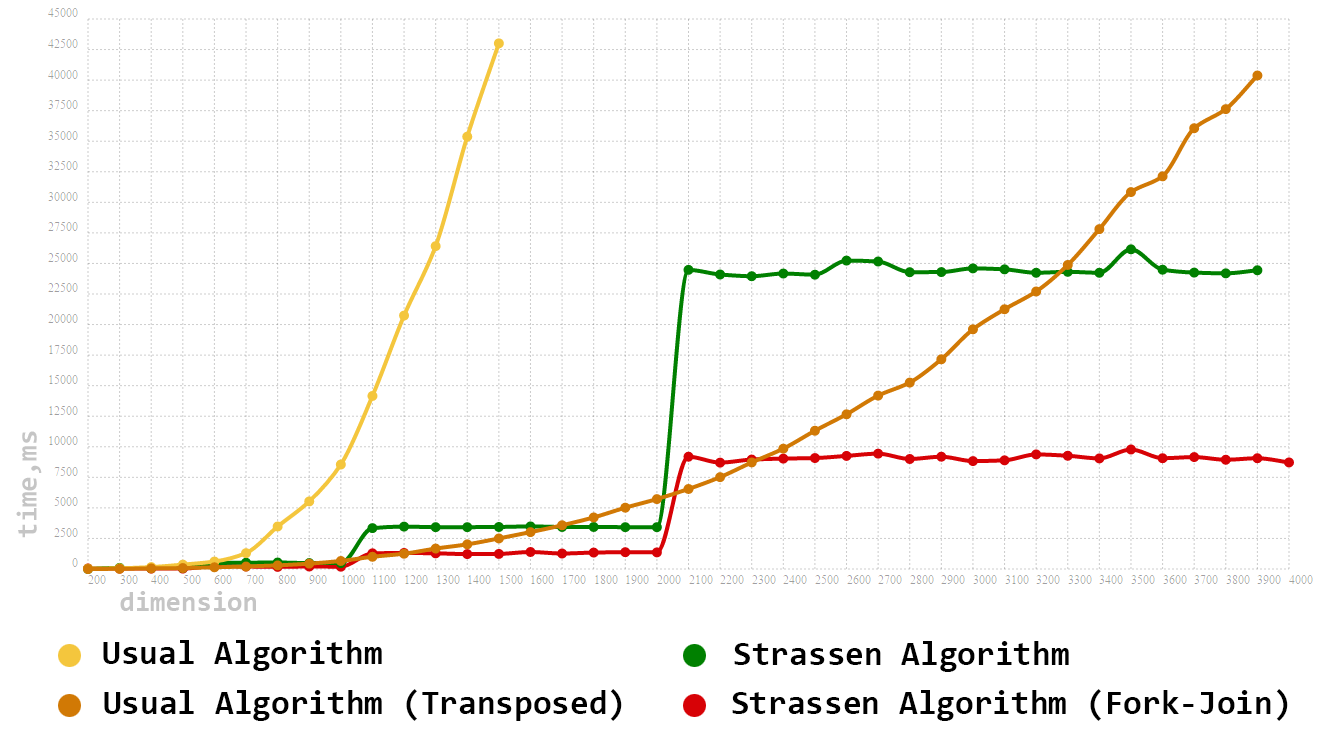
As expected, our first algorithm immediately fell out of the top three. But with his modernized brother (transposition version), not everything is so simple. Even on rather large dimensions, this algorithm is not only not inferior, but often exceeds the Strassen single-threaded algorithm. And yet, having a trump in the sleeve in the form of the Fork-Join Framework, we managed to get significant performance gains. Parallelization of the Strassen algorithm allowed us to reduce the multiplication time by almost 3 times, and also to head our final total.

The source code is available here .

We welcome feedback and comments to our work. Thanks for attention!