Category theory on javascript. Part 1. Category of sets

Abstraction is one of the main techniques in IT. Any programming or modeling language, any programming paradigm (procedural, functional, OOP, ...) give an answer to the question of how and from what to abstract. Moreover, the adherents of each approach offer some kind of abstraction of their own.

If you want to see a true, universal abstraction, then join our ... study category theory. The article on the example of the category of sets with pictures and JavaScript-code explains the most basic concepts of category theory: limits, universal property. The computational aspect of category theory is considered.
')
Also it says a little about classes, impurities and mixes in JavaScript.

Examples from the article can be found here .

Introduction

I think everyone heard about category theory. We heard that this is a cool silver-bullet theory, with which you can consistently describe very different things. We heard that it is actively used in functional programming languages. Some may have even heard of programming languages or computer algebra systems , largely based on category theory.

There are many books and articles on this subject on the Internet. But usually they are focused either on mathematicians or on IT scientists who are engaged in science and strange things like Haskell, ML (irony - I don’t need to put a minus in karma, as is usually the case after mentioning Saint Haskell in vain).

And for simple hard workers who earn their living on a piece of bread every day using JavaScript on JavaScript, the benefits of category theory are not very clear. I do not promise that after reading this series of articles it will become clearer. But if everything works out, then maybe we even have an application that will do something useful.

Immediately I warn you that I have an engineering, not a mathematical, education. Therefore, if you expect to see in the article strict definitions, proofs of theorems, etc., then you will not see. Rather, on the contrary, everything will be described "on the fingers." If you see any inaccuracies, please write, I can be wrong about something.

What is a category?

A category is anything that is defined for:

• feature class
• a class of morphisms (arrows) between objects (and, for each object, there is an identical morphism),
• operation of morphism,
  
  • which is associative:
    (h ∘ g) ∘ f = h (g ∘ f)
  • for which identical morphisms are neutral elements:
    f ∘ id _A = id _B ∘ f = f
  
  

The ∘ symbol is sometimes omitted: (h g) f = h (g f)

Also, instead of the composition, the concatenation of morphisms is sometimes used, so that in the formula they go in the same order as in the diagram: (f; g); h = f; (g; h) But such a recording is not as convenient as it seems, therefore it is rarely found. If we consider the elements in the following articles, you will be convinced of this.

To construct a category of something, you must

• think up what objects and morphisms will be in this category,
• do not forget about identical morphisms,
• think up what is the operation of the composition of morphisms,
• prove that the composition has the necessary properties
• ...
• profit.

Morphisms must have exactly one source and one target object. They can not connect 3 or more objects, can not "hang in the air." (We do not consider categories of higher orders .)

The operation of the composition can be applied only to compatible morphisms. Let there be morphisms f: A → B, g: B → C, and h: C → D. The composition g ∘ f (or f; g) is admissible. The following compositions are not allowed: h ∘ f, f ∘ f, f ∘ g.

Now consider an example category. Imagine an elementary topos, it is a category. If presented, it is unlikely that you will find in this article for yourself something new. It is better to read something more fundamental.

Example of free category generated by a graph

If you still continue to read, then try to construct a more understandable category. Submit your VKontakte page, as well as the pages of your friends, subscribers, and those you are following — everyone you are directly connected to. This will be the feature class :


For everyone you subscribe to, draw an arrow from your page to that person’s page. For everyone who is following you, draw an arrow from their pages to yours. And for all your friends, draw arrows in both directions:


Now do the same for the rest of the pages:


We assume that if one person is subscribed to another, then the first one knows the second. If two people are signed on each other (they are friends), then they know each other. Those. morphism in our category - this relationship "knows".

We assume that everyone knows themselves and draw identical morphisms :


We define the operation of the composition of morphisms as follows.

Let f be a morphism denoting that A knows B, and g is a morphism denoting that B knows C. Then g ∘ f is a morphism that means that A indirectly knows C.

Thus, the class of morphisms in our category includes not only the relation “knows”, but also “indirectly knows”.

The associativity of the operation of the composition is obvious. If A knows B, who knows C, who knows D, then how not to group morphisms here, anyway A indirectly knows D.

The fact that identical morphisms are neutral elements of the composition is also obvious. If A knows B, then the fact that they know themselves does not change anything.

We built a free category generated by a graph . On the one hand, this example shows how a category can be built from anything. On the other hand, it shows that categories are built according to certain rules.

Preorder example

In the previous example, the objects and morphisms are relatively simple, we believe that they have no internal structure.

Now imagine that all the pages (yours and the people with whom you are associated) are one object. The set of pages related to another person is another object, and so on:


What morphisms can be in this category?

For example, the "subset" relationship. If every friend, subscriber, etc. person A is also another subscriber, etc. of a person B, then draw a morphism from A to B. In this case we get a preorder , which is a category:


Or, for example, as morphisms, we can use functions that take pages as arguments and return some other pages for them. In this case, we get the category of sets. More precisely, its subcategory, because the category of sets contains all the sets, and not just the set of pages in VKontakte.

Commutative diagrams

In the examples reviewed, I identified diagrams with categories. But, in general, these are different things. Strictly speaking, a diagram is a functor. What is a functor for us is not important.

In one of the previous articles, we have already noted that a model and its presentation in some notation (a diagram, a textual representation or some other) are two different things. Similarly with categories.

For now, we will assume that a diagram is a kind of visual representation of a category fragment in which objects are depicted as nodes, and morphisms as arrows between nodes. However, the diagram can sometimes depict the entire category as a whole, and not just its fragment. There are categories containing only one or several objects and morphisms.

Diagrams can be commutative or noncommutative.

A commutative diagram is a diagram in which for any pair of objects the result of the composition of morphisms does not depend on the choice of a directed path between these objects.

Personally, I did not immediately understand how a diagram can be non-commutative. Look at the examples of the free category generated by the graph and the preorder above. If there are several paths between two objects, then obviously all these paths are equivalent - they begin with one object and end with one object. How can these paths be nonequivalent?

The fact is that in the preorder from a certain object A to a certain object B there can be at most one morphism. In a free category between a pair of objects there can be more than one morphism (see the discussion in the comments), but in this example it is intuitively clear that these morphisms are equivalent: they always reflect the fact that person A directly or indirectly knows person B. But, for example, in the category of sets between the same pair of objects there can be several completely different morphisms. Consider as an example a very simple diagram with two objects and two parallel morphisms. Is it commutative?


It will be commutative if and only if the equality f = g holds. In general, in category theory, commutative diagrams are often used as an alternative to writing systems of equations. You can write "the following equalities hold" and list them. Or you can write “the following diagram is commutative” and draw a diagram corresponding to the system of equations.

The commutativity of this diagram depends on what sets and functions are behind the drawn objects and morphisms. Let object A be a set of numbers, object B is a set of geometric figures, morphism f is a function that for some number returns a circle with a radius equal to that number, morphism g is a function that for some number returns a square with side length equal to this number. Obviously, these two functions are not equal, which means that the diagram is noncommutative:


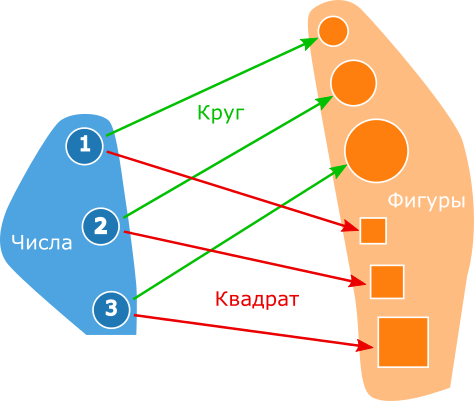
Do not be confused by the fact that in one category there are mixed sets of numbers and sets of figures. In the same category there can be sets of VKontakte pages, sets of sets, graphs, cats and anything else - all this is one category of sets. Let's look at it in more detail, but first, a little general information about the source code.

General Source Code Information

Source codes are available here , and examples from the article here .

Immediately I warn you that I wrote most of the code 3 years ago, when there was no ES6 yet, and there were no normal collections in the standard library. I then had to implement my Set. And, in general, the code is probably not very well organized. I honestly tried to decompose everything in modules, read the article and realized that category theory looks much simpler than all this tin.

In the Helpers.js file, along with other auxiliary functions, the extend and combine functions are defined. The extend function has long been invented, it allows you to inherit one class from another and is described in detail here . The only thing my implementation can add to the class of impurities. I highly recommend reading this article about impurities , where they are treated as factories of subclasses, described as they can be compactly described on ES6. In general, a look at impurities as a more general case of inheritance, in which the superclass is unknown in advance, is quite interesting.

Personally, I do not want to bother with Babel, etc., so the source code is written in ES5 and I needed these two functions. Impurities cannot be inherited as classes using extend; they can only be mixed using the combine method.

The category.js file defines an abstract category “category” from which specific categories must inherit. It also defines the impurities “full category” and “full category” and their mixture “bipolar category”. The category of sets, which we will consider below, is once again a bipolar category and some universal algorithms “mix in” with it, which can be used in any bipolar category. They are implemented precisely as impurities, because JavaScript does not support multiple inheritance. Further, all this is explained in more detail.

The file Set.js defines 1) the category of sets, 2) the sets themselves, 3) functions, and 4) some limits of the category of sets. Theoretically, the Set class can be replaced by Set from ES6. Functions are implemented in the form of so-called graphs , i.e. they explicitly store:

• admissible set of input elements - domain (domain of definition);
• the admissible result set is the code domain (range of values);
• set of pairs: input element and the corresponding result element.

The domain and code domain are stored explicitly so that you can check whether the composition of two functions is valid. It is valid only if the domain of the 1st function coincides with the code domain of the 2nd. Also, a domain is used when checking whether a function is indeed complete or it is a partially defined function . If you look at the code, there are a lot of similar checks (assert calls).

Probably, it is possible to store functions in the form of functions, rather than their graphs, but this is not important at all.

In the SetCategoryView.js file there is a d3 chart plotter for sets of categories. Almost all the illustrations in the article are drawn with its help. By the way, in the 4th version of d3 improved the Force Layout, now there you can independently determine arbitrary forces. Improved drag'n'drop, if I'm not mistaken, then before it worked only for svg, and now it is easily supported for canvas. Theoretically you can find something interesting in this drawing, but it requires full refactoring.

In the file Set.html all the examples from this article.

The implementation of the category of sets

Further I will describe various constructions from the category of sets and how they are implemented in the code. It itself is implemented in the form of the following factory:

function SetCategory() { } extend(SetCategory, Category, BicompleteCategory); SetCategory.prototype.object = function (elements) { return new Set(elements); }; SetCategory.prototype.morphism = function (A, B, mapping) { return new TotalFunction(A, B, mapping); }; SetCategory.prototype.id = function (A) { return this.morphism(A, A).initId(); }; SetCategory.prototype.compose = function (g, f) { return g.compose(f); }; 

The category of sets is inherited from an abstract category and the behavior of the bipolar category is mixed with it.

This factory allows you to create

• objects (which are sets);
• morphisms (which are functions that map the elements of some set A to the elements of some set B);
• identical morphisms (which are the identity mappings of some set A onto itself);
• compositions of two morphisms.

Frankly, I did not immediately realize why categories should be factories. For example, sets, lists, stacks, trees, graphs, and other structures usually explicitly store all their elements. Categories are like similar mathematical structures, but why are they implemented differently? Why is it impossible to implement a category as a repository of its objects and morphisms? Because in the general case a category contains an infinite number of objects and morphisms. Moreover, of them we need only a few. And they need not so much to store as to construct on their basis new objects and morphisms.

Create several objects and morphisms:

 var setCat = new SetCategory(); var obj123 = setCat.object([1,2,3]); var objAB = setCat.object(['a','b']); var objABCD = setCat.object(['a','b','c','d']); var f = setCat.morphism(obj123, objABCD, {1: 'c', 2: 'c', 3: 'd'}); var g = setCat.morphism(objABCD, objAB, {'a': 'a', 'b': 'b'}); var h = setCat.morphism(objAB, obj123, {'a': 1, 'b': 1}); showSetCategoryView('diagram1', setCat, {'A': obj123, 'B': objABCD, 'C': objAB}, {'f': {dom: 'A', codom: 'B', morphism: f}, 'g': {dom: 'B', codom: 'C', morphism: g}, 'h': {dom: 'C', codom: 'A', morphism: h}}); 

It is a pity that you can not insert into the article executable JavaScript code. Therefore, it is necessary to insert pictures, but I repeat that you can move all this here .

Epimorphism, monomorphism, isomorphism

Ok, we can create objects, morphisms and draw them beautifully. What's next?

Objects and morphisms may have different properties, and a significant part of category theory is devoted to the description and study of these properties. Our implementation of category theory should be able to verify these properties and should be able to construct objects and morphisms with certain properties. Let's start with the simplest properties.

Let me remind you that morphisms in the category of sets are functions. From school, you probably remember that functions can be surjections, injections, bijections. I promised that there will be no strict definitions and everything will be explained on the fingers, so get:

A surjection is a function that takes all the values ​​from its range of values. Say, the squaring function defined on a set of integers is not a surjection because it does not take the value 2, 3, 5, ...


An injection is a function that maps different elements of the original set to different elements of the result set. In this case, the range of the function may contain some additional elements that do not have a pre-image in the definition area.


Bijection is a one-to-one mapping. A function is a bijection if and only if it is simultaneously a surjection and an injection.


For other mathematical objects (for example, graphs) there are some analogs of surjections, injections and bijections. Therefore, in the theory of categories, since this theory is about everything, they decided to generalize these concepts and introduced epimorphisms, monomorphisms and isomorphisms, respectively.

What is this generalization? In that in the theory of categories we completely abstract away from the internal structure of objects and morphisms. Instead of defining these types of morphisms through circles and arrows, as is done in the figures above, they are defined in terms of relationships with other morphisms.

An epimorphism is a morphism e: A → B, such that f ∘ e = g ∘ e follows from any equality f = g (in other words, e can be shortened to the right).


To make it clear what is being said, I will give an example of NOT epimorphism:


The diagram above is commutative (f ∘ h = g ∘ h). To make sure of this, you can follow the arrows from each element of the set A and, regardless of the chosen path, you always come to the same element of the set C. Ie functions f ∘ h and g ∘ h for identical arguments return identical results. But (!) This does not imply the equality of the functions f and g. For the element "1" they return different values: "a" and "b". But, if the function h were an epimorphism, then the commutativity of the diagram would imply the equality f and g.

Further, I will not describe in detail “the transitions by arrows through circles”, just keep in mind that when in the category of sets we are talking about commutative diagrams, you can always check this commutativity in this way.

I note once again that we have described surjective functions only through correlation with other functions, completely abstracting from the details of their internal structure. This is the essence of category theory.

A monomorphism is a morphism m: A → B, such that from every equality m m f = m g it follows f = g (in other words, m can be abbreviated to the left).


An isomorphism is a morphism f: A → B for which the inverse exists, that is, there exists a morphism g: B → A such that f ∘ g = id _B and g ∘ f = id _A.


Here, here is a little surprise. Not in all categories from the fact that the morphism is an epimorphism and a monomorphism it follows that it is also an isomorphism. This demonstrates that the category of sets is certainly good for visualizing some concepts, but can lead to false analogies.

End, Start, and Zero Object

The final object is an object T such that for any object X there exists a unique morphism u: X → T.

In the category of sets, the final object is a singleton, and a unique morphism is a function that maps any element of the original set to a single element of a singleton. There are an infinite number of terminal objects in the category of sets; however, they are all isomorphic to each other. This means that from the point of view of category theory it does not matter which particular singlet is being spoken of, everything that is true for one up to isomorphism will be true for any other singleton.


The initial object is the object I, such that for any object X there exists a unique morphism u: I → X.

In the category of sets, the initial object is an empty set, and a unique morphzyme defined on an empty set is an empty function. Moreover, there is a unique empty set, respectively, in the category of sets a single initial object.


A null object is an object that is both the initial and the final object.

There are no zero objects in the category of sets, since the set cannot be simultaneously empty and singleton.

We note several important points.

The initial and final objects are dual concepts, they are equivalent up to the inversion of the direction of morphisms. The initial object will be the final object in the dual category (categories with the same objects and the operation of composition, but with morphisms directed in the opposite direction). The idea of ​​duality or duality is very important in category theory. Further you will see some more examples of dual concepts.

By the way, the end objects can be called konachalnymi, and the initial - kokonechnye, but here we already fall into the domain of one fundamentally new programming language . If we add or remove the prefix "ko-" from the concept, we get a dual concept. I did not meet cocooned objects, although a category theory specialist must understand that we are talking about initial objects.

In the definitions above, nothing is said about morphisms directed from the final object. And they exist. For example, a certain morphism f: {1} → {1,2,3,4} with the graph {(1,1)} or the morphism g with the same signature, but the graph {(1,2)}. Those. they not only exist, but are not yet unique, and, looking ahead, play quite an important role. Therefore, the idea of ​​final objects as objects whose morphisms are directed only to them is not true.


As for the morphisms directed to the initial objects, I cannot say anything. I assume that in the category of sets they are either not present or they are empty unique functions. In principle, why should they not be. But then, each set will be isomorphic to the empty set. If someone could clarify this point, it would be great.

Universal property and the most important point

Pay attention to the phrase "... there is a single morphism ..." in the definitions above. It is commonly found in works on category theory. This is called the " universal property ."

Universal property allows you to define the concept, abstracting from the details. You see that the initial and final objects are defined without mentioning empty sets, singletones, yes, and, in general, any structures. Here, this is a real abstraction! I think that in the category theory guides for developers, you need to talk first of all about such things, and not about Cartesian closed categories or monads .

In other words, in the theory of categories you define objects, focusing not on the description of their internal implementation, but on the description of their external behavior, how they can “interact” with other objects, in fact, you describe their interface. True, a little differently than it is usually done in programming languages, but this theory of categories is also interesting.

Due to abstraction from details, the universal property defines an object up to isomorphism. We have already noted above that in the category of sets, all finite objects (singletons) are isomorphic. But this is true for any objects defined through the universal property. In principle, this is quite logical: if two objects outwardly "behave" in the same way (one universal property holds for them), then they are isomorphic.

And, probably, the most important point that underlies this entire series of articles. Behind universal properties there is usually some optimization problem, which consists in finding the best in some sense objects or morphisms. We will return to this in the section about equalizers.

Implementing end and start objects

You may have a question: why so much code to implement a singleton and NULL set ???

The final and initial objects are not just some sets. For them, the universal property must also be satisfied, which is not of some theoretical nature, but it is actively used in calculations. For example, when calculating an addition to a codecard square, a universal morphism is calculated for the sum of the objects. We will come back to this later.

In our implementation, constructions with a universal property will have methods:

• calculate - creates some universal construction or assembles it from other constructions,
• complement - creates a universal structure from not very typical components,
• univ - calculates universal morphisms for this construction.

Composition

We continue the loose definitions on the fingers and consider slightly more complex objects.

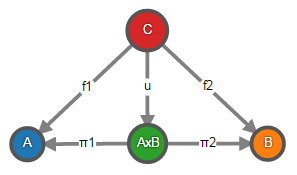
The product of objects X _j is an object X and morphisms π _j : X → X _j , called canonical projections, such that for any object Y and morphisms f _j : Y → X _j there exists a unique morphism u: Y → X, such that π _j ∘ u = f _j .

In category theory, instead of writing equations of the form π _j ∘ u = f _j, you can draw a similar diagram and say that it is commutative (an example for two objects, but in the general case there may be more):


In the category of sets, the product of objects is the Cartesian product of sets.


In the picture, the product is designated as AxB, and its elements as pairs of elements from the original sets. But this is done for clarity and not necessarily! The work can be called as you like, and its elements can be

• 1, 2, 3, ...
• square, circle, triangle, ...
• or whatever.

The product is defined not as a set of pairs of values, but through relations between morphisms. Compare the definitions of the Cartesian product of sets and the product of objects in category theory — they have nothing in common. You again see an example of abstraction from details in category theory.


Note that in the calculate function, not only the Cartesian product of sets is calculated, but also two morphisms — canonical projections of the product onto the original objects. In most calculations, they play the main role and, roughly speaking, they are much more important than the set.

The univ function calculates a universal morphism (u is in the diagram above) for some object and a pair of morphisms. Let's see how a universal morphism of a work can be useful.

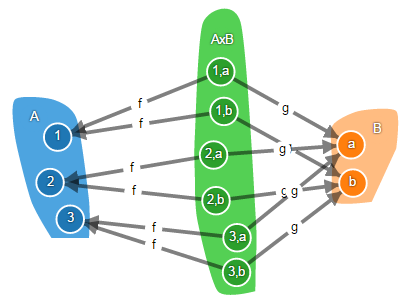
In the following diagram, you see objects A and B, their product AxB, and also some arbitrary object C with morphisms f ₁ and f ₂ .


You can see that the element “1” of the set C is mapped to the element “1” of the set A and to the element “a” of the set B. Just like the element “1, a” of the set AxB. When calculating a universal morphism, we set this fact and construct a universal morphism so that it maps the element “1” of the set C to the element “1, a” of the set AxB.

The elements “4” and “5” of the set C are mapped by f ₁ and f ₂ morphisms onto the same elements. Therefore, the universal morphism maps them to one element “2, b” of the set AxB.

For clarity, imagine that C is the set of monkeys. f ₁ each monkey belongs to one of the categories: beautiful or ugly, and f ₂ to one of the categories: smart or stupid. Then the universal morphism u refers each monkey to one of four categories: beautiful and intelligent, beautiful and stupid, ugly and intelligent, ugly and stupid.

In fact, the universal morphism for a work is a product of morphisms.

The work in different forms is implemented in various programming languages. These are structures, tuples, and all sorts of joines in SQL, LINQ, etc. Read about the types of works .

In JavaScript, canonical projections of a work can be viewed as destructors or accessors:

 monkeyKind.a monkeyKind.b 

and universal morphisms as constructors:

 function u(x) { return { a : isBeautiful(x), b : isSmart(x) }; } 

In the theory of categories, accessors are often called destructors, because they make it possible to disassemble a complex object into its component parts, they are dual to designers. When you call such a destructor object does not necessarily have to be destroyed.

Amount

The sum of objects X _j is an object X and morphisms i _j : X _j → X, called canonical embeddings, such that for any object Y and morphisms f _j : X _j → Y there exists a unique morphism u: X → Y, such that u ∘ i _j = f _j .

An example of a commutative diagram for two objects:


In the category of sets, the sum of objects is the disjunctive union of sets. Those. if there are coinciding objects in the merged sets, then these objects will not merge, but, roughly speaking, will be marked in some way so that you can understand from which set each object.


In set theory, elements of a disjunctive union are usually tagged with some tags or indices, for example, 1 _A , 2 _A , 3 _A , a _B , b _B. But in our example, the elements of the sum are simply numbers from 1 to 5, which are associated with the elements of the original set by the morphisms f and g. And it is these morphisms that "tag" the elements of the sum. As for the work, the set itself without morphisms does not play a special role.

Obviously, the product and the sum are dual concepts. They are formulated in a similar way up to inversion of morphisms.

But this generalization does not end there. The product and the sum are very similar to the final and initial objects, respectively. For products and finite objects, it is possible to construct a universal morphism from each category object satisfying certain conditions — such constructions are called limits . For the sum and the initial object, it is possible to construct a universal morphism for each category object that satisfies certain conditions — such constructions are called constraints . Further you will see some more examples of limits and values.

In the general case, (ko) limits are (ko) cones defined for some diagram. As I said before, a diagram is a functor from some index category to the current category. If roughly, then the index category determines the “form”, “type” of the diagram and ultimately determines what (co) limit we will get (the final object, the product, ...). If we further develop this thought, then we risk calling a cacdemoon.



In short, the idea is that even such general concepts as we discussed above can be generalized even more.

, , , () «» . .


, .


, , – . – .

, , – . - . . , . JavaScript , .

– – :

 function Chimpanzee() { } function Gorilla() { } 

p, – q, – C. , C – : , , . p , , q :

 function u(x) { if (x instanceof Chimpanzee) { return p(x); } else if (x instanceof Gorilla) { return q(x); } } 

( )

- , - . , , ? , , coproduct complement. . , , .

A+B, A i ₁ . i ₁ , A, – A+B. i ₂ , :



N-, . . .

() ( ) ( ). () , .. .

f, g : X → Y – E eq : E → X, f ∘ eq = g ∘ eq O m : O → X f ∘ m = g ∘ m, u : O → E, eq ∘ u = m, .. .


… . - . . -, , , . , , . , . -, , . - . .

f ∘ eq = g ∘ eq. X eq , f g .


f g «1» X «a» Y. , eq «1» E «1» X, f(eq(1)) = g(eq(1)) = a. , , «1» E, Y.

f «2» «a», g «2» «b». , eq, «2» X . Those. f(eq(?)) = a g(eq(?)) = b, «a» «b».

X Y E eq. «1» «3» f g .

, E eq - f g. O m u? , E eq, , . O m, f ∘ m = g ∘ m.


, m f g , eq. eq m? . , E eq , O m , , . , , , , . - , , .

, ? . E O h, m ∘ h = eq, {(1,1),(3,3)} {(1,2),(3,3)}. , , O m , .

, , E eq - . O m u = {(1,1),(2,1),(3,3)}. O m, f ∘ m = g ∘ m, , .

O m E eq? ? , .

, , JavaScript! , , , ().


. , – . , f ∘ eq = g ∘ eq f ∘ m = g ∘ m … . , , ? .

f = g. , , , f g. , , , . , . f g , eq ( ).

, ? . O E . , , – ( ), , .

? , «» , (, ) . , , .

f, g : X → Y – Q q : Y → Q, q ∘ f = q ∘ g O m : Y → O m ∘ f = m ∘ g, u : Q → O, u ∘ q = m, .. .


, , . , , , , .

.


f g, , «1» X «a» Y. q(f(1)) = q(g(1)), , q «a» «a» Q.

f «2» «b», g «2» «c». q(f(2)) = q(g(2)), q «b» «c» «b» Q. , «b» «c» «b».

f «3» «c», g «3» «d». , , «c» «d» . «c» «b», , «d» «b».

«e» «e» «f». Q q.

, , O m, m ∘ f = m ∘ g. , O m , Q q.


O m , , , Q q. , , «a» «b», «1».

, . – . , () .


– . : , , . . .

( )

. , , ? – .

f : X → Z g : Y → Z – P p : P → X q : P → Y, f ∘ p = g ∘ q Q m : Q → X n : Q → Y, f ∘ m = g ∘ n, u : Q → P, p ∘ u = m q ∘ u = n, .. .


, - :


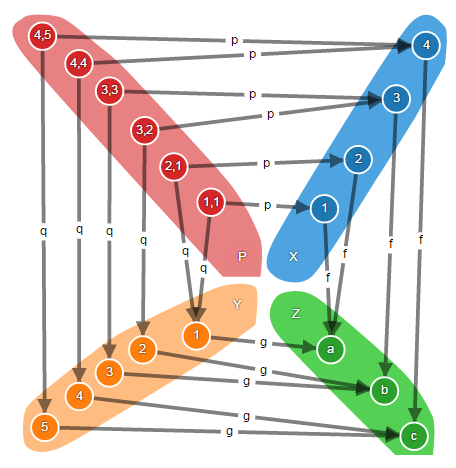
, P X Y, , , , f g Z.

, , , .


. X Y, f ∘ π ₁ g ∘ π ₂ . – P . p π ₁ ∘ eq, q – π ₂ ∘ eq. .


, : , , .. , , , . , . , , .

( )

f : Z → X g : Z → Y – P p : X → P q : Y → P, p ∘ f = q ∘ g Q m : X → Q n : Y → Q, m ∘ f = n ∘ g, u : P → Q, u ∘ p = m u ∘ q = n, .. .


i ₁ ∘ f i ₂ ∘ g, i ₁ i ₂ – X Y. p q h ∘ i ₁ h ∘ i ₂ , h – :


, P – X Y, , Z, :


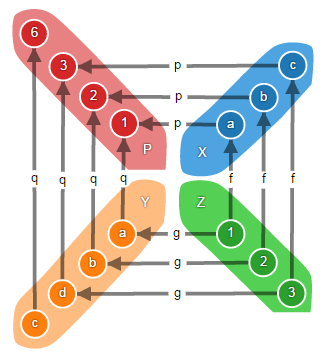
. , «a» «b» X Y P «1» «2» . «c» X «d» Y. «c» Y .

. g q. f p, X P , Y. . .

, (, , ) , :

, , , JavaScript ML:
» DE Rydeheard, RM Burstall. Computational Category Theory, 1988

, :
» Hans Jürgen Schneider. Graph Transformations. An Introduction to the Categorical Approach, 2011

, , , , , :
» Peter Smith, Category Theory. A Gentle Introduction, 2016

, :
» Maarten M. Fokkinga. A Gentle Introduction to Category Theory — the calculational approach, 1994

, :
» Andrea Asperti, Giuseppe Longo. Categories, Types and Structures. Category Theory for the working computer scientist, 1991
» Michael Barr, Charles Wells. Category Theory for Computing Science, 1998

, « » ( — Bartosz Milewski ), , , , . , .

. , , . , . — . , , . , , , 1- :
» Michael Barr, Charles Wells. Toposes, Triples and Theories, 1985

, , David I. Spivak . , .

:
» Michael J. Healy. Category Theory Applied to Neural Modeling and Graphical Representations, 2000

Conclusion

. , , , . , .

, . . , Haskell Hask. . , , . . . - .

. , , , . . , , , .

, – , , .

.

-, , . , calcCartesianProduct(), - multiplyFunctions(). , , — . Those. .

-, , , .

-, , . , ( assert ). , - , !

, , . , , , , . , . «», .

, - JavaScript.

. , .

» .