Welcome to the second part of the neural network guide. Just want to apologize to all who waited for the second part much earlier. For certain reasons, I had to postpone its writing. In fact, I did not expect that the first article would have such a demand and that so many people would be interested in this topic. Taking into account your comments, I will try to provide you with as much information as possible and at the same time keep the most understandable way to present it. In this article, I will talk about the ways of teaching / training neural networks (in particular, the method of reverse propagation) and if you, for whatever reason, have not yet read the first part , I strongly recommend starting with it. In the process of writing this article, I also wanted to talk about other types of neural networks and training methods, however, starting to write about them, I realized that this would go against my presentation method. I understand that you are not eager to get as much information as possible, however these topics are very extensive and require detailed analysis, and my main task is not to write another article with a superficial explanation, but to bring to you every aspect of the topic touched and make the article as easy as possible. mastering. I hasten to upset the fans of "cool", since I still will not resort to the use of a programming language and will explain everything on my fingers. Enough entry, let's now continue to study neural networks.

What is a neuron bias?

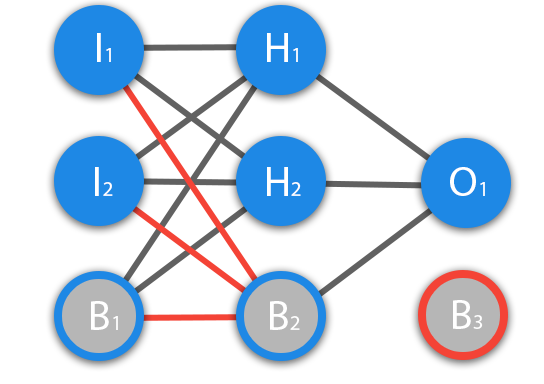
Before we begin our main topic, we must introduce the concept of another type of neuron - the displacement neuron. The displacement neuron or bias neuron is the third type of neuron used in most neural networks. The peculiarity of this type of neuron is that its input and output always equal 1 and they never have input synapses. Neurons of displacement can either be present in the neural network one by one on the layer, or completely absent, 50/50 cannot be (red on the diagram indicates weights and neurons that cannot be placed). Connections in neurons of displacement are the same as in normal neurons - with all neurons of the next level, except that there can be no synapses between two bias neurons. Consequently, they can be placed on the input layer and all hidden layers, but not on the output layer, since they simply will not have anything to form a connection with.

What is a displacement neuron for?

Neuron bias is needed in order to be able to get the output by shifting the graph of the activation function to the right or left. If this sounds confusing, let's consider a simple example where there is one input neuron and one output neuron. Then you can establish that the output O2 will be equal to the input H1 multiplied by its weight, and passed through the activation function (the formula in the photo on the left). In our particular case, we will use sigmoid.
')
From the school course of mathematics, we know that if we take the function y = ax + b and change the values ​​of “a” for it, the slope of the function will change (the colors of the lines in the graph on the left), and if we change the “b”, we will shift function to the right or left (the colors of the lines in the graph on the right). So "a" is the weight of H1, and "b" is the weight of the displacement neuron B1. This is a rough example, but this is how it works (if you look at the activation function on the right of the image, you will notice a very strong similarity between the formulas). That is, when during training, we adjust the weights of hidden and output neurons, we change the slope of the activation function. However, the regulation of the weight of the neurons of displacement can give us the opportunity to shift the activation function along the X axis and capture new areas. In other words, if the point responsible for your decision is located, as shown in the graph on the left, then your NA will never be able to solve the problem without using displacement neurons. Therefore, you rarely find neural networks without neuronal displacement.

Also, displacement neurons help when all input neurons receive input 0 and no matter what weight they have, they will all pass to the next layer 0, but not if there is a displacement neuron. The presence or absence of displacement neurons is a hyperparameter (more on this later). In a word, you yourself have to decide whether you need to use displacement neurons or not, banishing NA with and without mixing neurons and comparing the results.

It is IMPORTANT to know that sometimes on the circuits they do not indicate displacement neurons, but simply take their weights into account when calculating the input value for example:

input = H1 * w1 + H2 * w2 + b3
b3 = bias * w3

Since its output is always 1, you can simply imagine that we have an additional synapse with weight and add this weight to the sum without mentioning the neuron itself.

How to make the National Assembly give the correct answers?

The answer is simple - you need to train her. However, no matter how simple the answer, its implementation in terms of simplicity, leaves much to be desired. There are several methods of teaching NA and I will highlight 3, in my opinion, the most interesting:

• Back Propagation Method
• Elastic propagation method (Resilient propagation or Rprop)
• Genetic Algorithm (Genetic Algorithm)

About Rprop and GA will be discussed in other articles, and now we will look at the basis of the basics - backpropagation method that uses the gradient descent algorithm.

What is a gradient descent?

This is a way to find the local minimum or maximum of a function by moving along a gradient. If you understand the essence of the gradient descent, then you should not have any questions while using the back propagation method. To begin with, let's see what the gradient is and where it is present in our NA. Let's build a graph, where the x-axis will be the weight values ​​of the neuron (w) and the y-axis is the error corresponding to this weight (e).


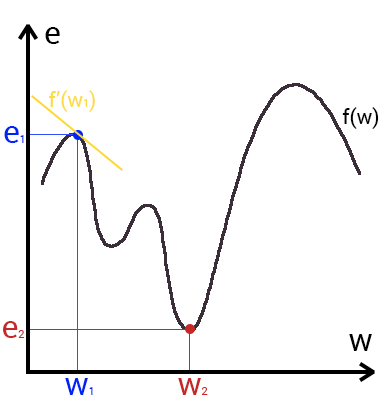
Looking at this graph, we understand that the graph function f (w) is the dependence of the error on the selected weight. On this chart, we are interested in the global minimum - a point (w2, e2) or, in other words, the place where the graph comes closest to the x-axis. This point will mean that choosing the weight w2 we get the smallest error - e2 and as a result, the best result possible. The gradient descent method will help us find this point (the yellow gradient in the graph). Accordingly, each weight in the neural network will have its own graph and gradient, and each one must find a global minimum.

So what is this gradient? Gradient is a vector that determines the slope steepness and indicates its direction relative to any of the points on the surface or graph. To find the gradient you need to take the derivative of the graph at a given point (as shown in the graph). Moving in the direction of this gradient, we will smoothly roll down to the lowland. Now imagine that an error is a skier, and a graph of a function is a mountain. Accordingly, if the error is 100%, then the skier is at the very top of the mountain, and if the error is 0%, then in the lowland. Like all skiers, the error tends to go down as quickly as possible and reduce its value. In the final case, we should have the following result:


Imagine that a skier is thrown onto a mountain with a helicopter. How high or low depends on the case (just as in a neural network when we initialize weights are placed in a random order). Suppose the error is 90% and this is our point of reference. Now the skier needs to go down using the gradient. On the way down, at each point we will calculate the gradient, which will show us the direction of descent and, when the slope changes, adjust it. If the slope is straight, then after the nth number of such actions we will reach the lowlands. But in most cases the slope (graph of the function) will be wavy and our skier will face a very serious problem - a local minimum. I think everyone knows what a local and global minimum of function is, for refreshing memory, here is an example. Getting into a local minimum is fraught with the fact that our skier will forever remain in this lowland and never slide down the mountain, therefore we can never get the right answer. But we can avoid this by equipping our skier with a jetpack called the moment (momentum). Here is a brief illustration of the moment:



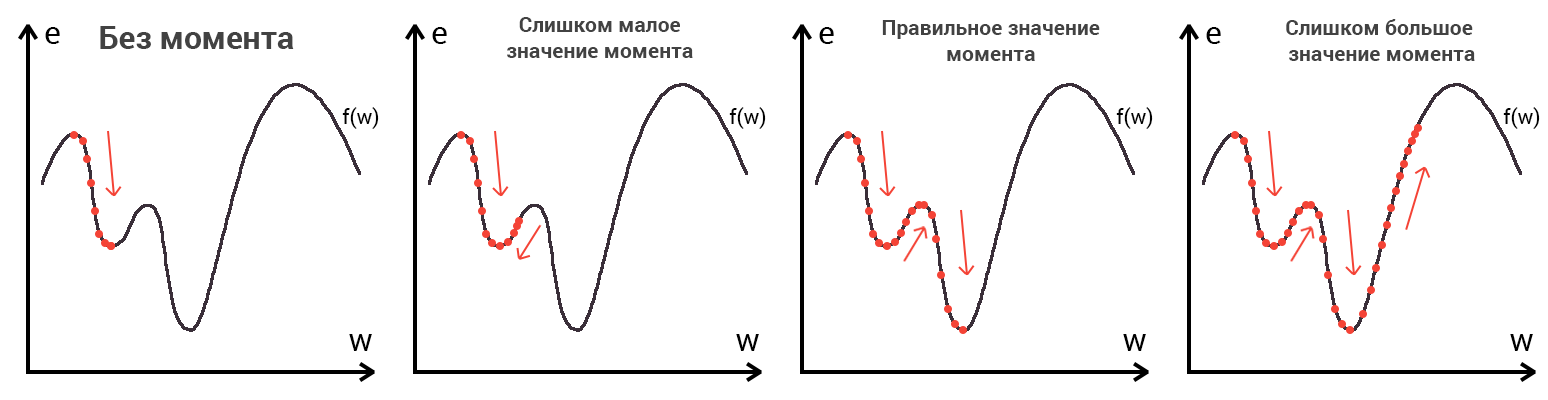
As you probably already guessed, this backpack will give the skier the necessary acceleration to overcome the hill that keeps us at a local minimum, but there is one BUT here. Imagine that we set a certain value to the moment parameter and easily managed to overcome all local minima and get to the global minimum. Since we cannot simply turn off the jet pack, we can slip through the global minimum if there are lowlands next to it. In the final case, this is not so important, because sooner or later we will still return back to the global minimum, but it is worth remembering that the greater the moment, the greater will be the scope with which the skier will ride through the lowlands. Together with the moment, such a parameter as the learning rate (learning rate) is also used in the back propagation method. As many will probably think, the greater the learning speed, the faster we will train the neural network. Not. The speed of learning, as well as the moment, is a hyperparameter - a quantity that is selected by trial and error. The speed of learning can be directly linked with the speed of a skier, and you can say with confidence that you’re going slower you will continue. However, there are also certain aspects here, because if we do not give the skier speed at all, he will not go anywhere at all, and if we give a small speed, the travel time can take a very, very long period of time. What then happens if we give too much speed?


As you can see, nothing good. A skier will begin to slip down the wrong path and maybe even in a different direction, which, as you understand, only keeps us away from finding the right answer. Therefore, in all these parameters, it is necessary to find a middle ground to avoid non-convergence of the NA (more on that later).

What is the Back Propagation Method (MPA)?

So we have come to the point where we can discuss how all the same to do so that your NA can properly learn and make the right decisions. Very good MOR visualized on this gif:

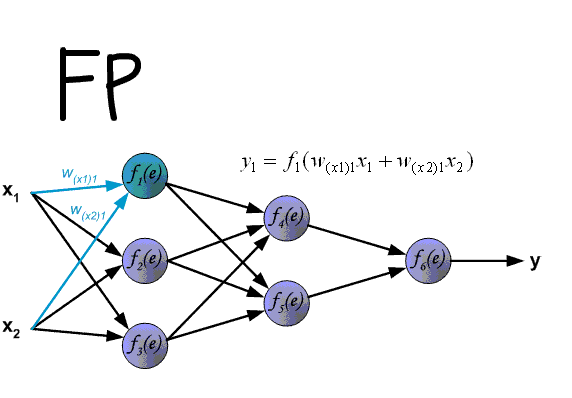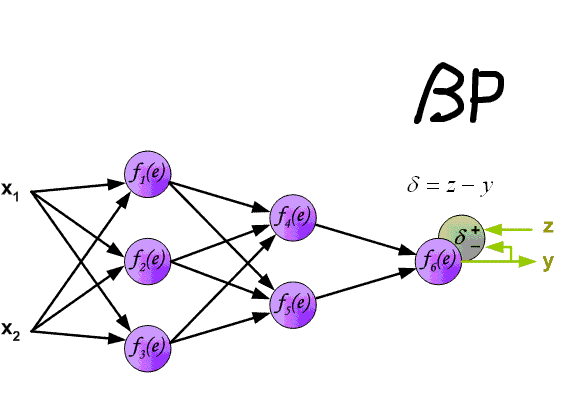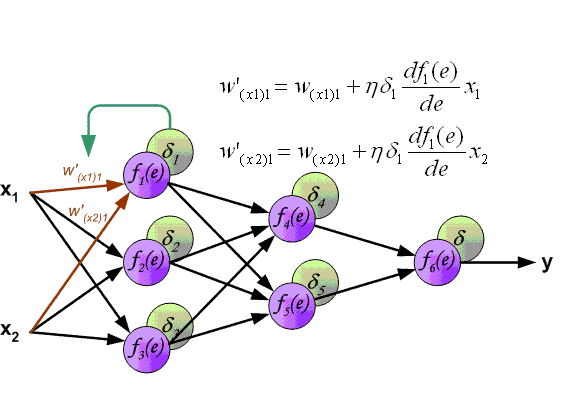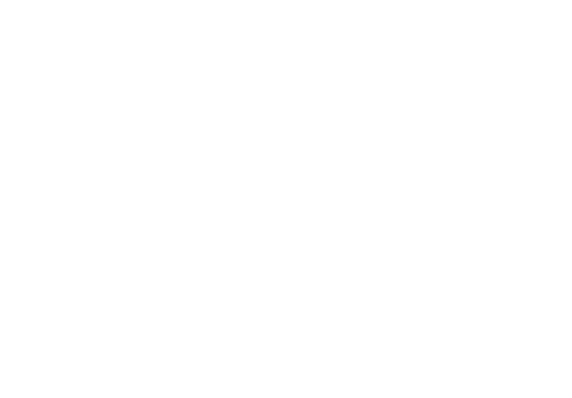
And now let's take a detailed look at each stage. If you remember that in the previous article we considered the output of the National Assembly. In another it is called forward transmission (Forward pass), that is, we consistently transmit information from the input neurons to the output. After that, we calculate the error and based on it we make a reverse transmission, which is to consistently change the weights of the neural network, starting with the weights of the output neuron. The value of weights will change in the direction that will give us the best result. In my calculations, I will use the delta method, as this is the easiest and most understandable way. I will also use the stochastic method of updating weights (more on this later).

Now let's continue from where we completed the calculations in the previous article.


Since we have already calculated the result of the NA and its error, we can immediately proceed to the MPA. As I mentioned earlier, the algorithm always starts with the output neuron. In this case, let's calculate for it the value δ (delta) by the formula 1.
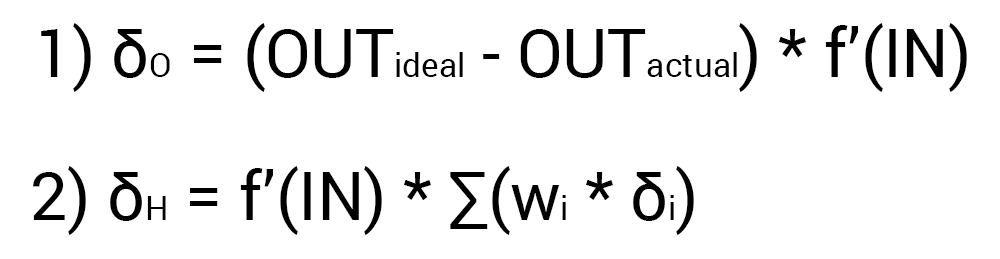Since the output neuron does not have outgoing synapses, we will use the first formula (δ output), so for the hidden neurons we will already take the second formula (δ hidden). Everything is quite simple here: we consider the difference between the desired and the obtained result and multiply by the derivative of the activation function of the input value of the neuron. Before proceeding to the calculations, I want to draw your attention to the derivative. First of all, as it has already become clear, with MPA, only those activation functions that can be differentiated should be used. Secondly, in order not to do extra calculations, the derivative formula can be replaced with a more friendly and simple formula of the form: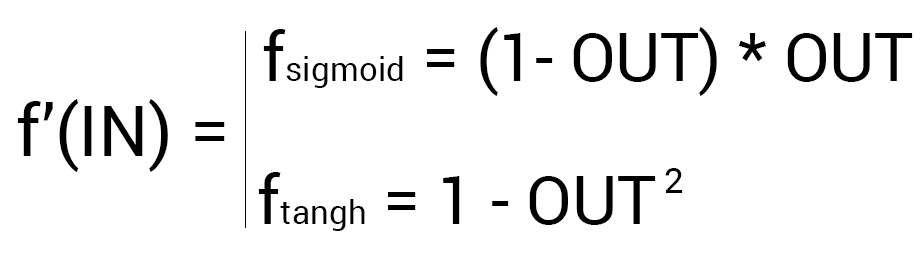

Thus, our calculations for the O1 point will be as follows.


This completes the calculations for the O1 neuron. Remember that after counting the delta of a neuron, we are obliged to immediately update the weights of all outgoing synapses of this neuron. Since in the case of O1 there are none, we go to the neurons of the hidden level and do the same for the exception that the delta calculation formula is now our second and its essence is to multiply the derivative of the activation function from the input value by the sum of the products of all outgoing weights and delta of the neuron with which this synapse is connected. But why are the formulas different? The fact is that the whole essence of the MPA is to spread the error of the output neurons to all the weights of the NA. The error can be calculated only at the output level, as we have already done, we also calculated the delta in which this error already exists. Consequently, now instead of an error we will use a delta which will be transmitted from the neuron to the neuron. In this case, let's find the delta for H1:


Now we need to find the gradient for each outgoing synapse. Here they usually insert a 3-story fraction with a bunch of derivatives and other mathematical hell, but that's the beauty of using the delta calculation method, because ultimately your gradient formula will look like this:

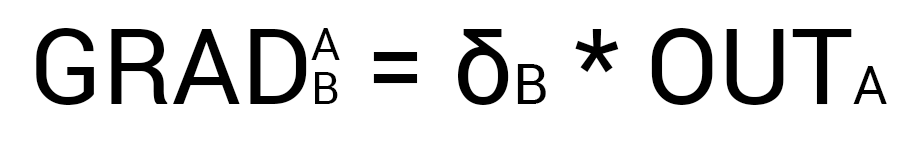
Here point A is the point at the beginning of the synapse, and point B at the end of the synapse. Thus, we can calculate the w5 gradient as follows:


Now we have all the necessary data to update the weight of w5 and we will do this thanks to the MPA function which calculates the value by which this or that weight needs to be changed and it looks like this:

I strongly recommend that you do not ignore the second part of the expression and use the moment as this will allow you to avoid problems with the local minimum.

Here we see 2 constants about which we already spoke, when we considered the gradient descent algorithm: E (epsilon) - learning rate, α (alpha) - moment. Translating the formula into words we get: the change in the weight of the synapse is equal to the coefficient of learning speed multiplied by the gradient of this weight, add the moment multiplied by the previous change of this weight (at the 1st iteration is 0). In this case, let's calculate the weight change w5 and update its value by adding Δw5 to it.


Thus, after applying the algorithm, our weight increased by 0.063. Now I suggest you do the same for H2.


And of course, we don’t forget about I1 and I2, because they also have weight weights that we also need to update. However, remember that we do not need to find deltas for input neurons since they do not have input synapses.


Now let's make sure that we did everything correctly and again calculate the output of the National Assembly only with updated weights.


As we see after one iteration of the MPA, we managed to reduce the error by 0.04 (6%). Now you need to repeat it again and again until your mistake is small enough.

What else do you need to know about the learning process?

A neural network can be trained with and without a teacher (supervised, unsupervised learning).

Teaching with a teacher is a type of training inherent in such problems as regression and classification (we used them in the example above). In other words, here you play the role of a teacher and the National Assembly as a student. You provide the input data and the desired result, that is, the student looking at the input data will understand that you need to strive for the result that you provided him.

Teaching without a teacher - this type of learning is less common. There is no teacher here, so the network does not get the desired result or their number is very small. Basically, this type of training is inherent in NSs whose task is to group data according to certain parameters. Suppose you submit to the input 10,000 articles on Habré and after analyzing all these articles, the National Assembly will be able to distribute them into categories based, for example, on frequently occurring words. Articles that mention programming languages, to programming, and where such words as Photoshop, to design.

There is also such an interesting method as reinforcement learning. This method deserves a separate article, but I will try to briefly describe its essence. This method is applicable when we can, based on the results obtained from the National Assembly, give it an assessment. For example, we want to teach the National Assembly to play PAC-MAN, then each time the National Assembly will score a lot of points, we will encourage it. In other words, we give the National Assembly the right to find any way to achieve the goal, as long as it gives a good result. In this way, the network will begin to understand what they want to achieve from it and is trying to find the best way to achieve this goal without constantly providing data by the “teacher”.

Also, training can be done in three ways: the stochastic method (stochastic), the batch method (batch) and the mini-batch method (mini-batch). There are many articles and studies on which method is better and no one can come to a common answer. I’m a supporter of the stochastic method, but I don’t deny the fact that each method has its pros and cons.

Briefly about each method:

The stochastic (sometimes called online) method works according to the following principle - found Δw, immediately update the corresponding weight.

The batch method works differently. We summarize Δw of all weights at the current iteration and only then we update all weights using this sum. One of the most important advantages of this approach is a significant saving in computational time, but the accuracy in this case can suffer greatly.

The mini-batch method is the golden mean and tries to combine the advantages of both methods. Here the principle is as follows: we in a free order distribute weights into groups and change their weights by the sum Δw of all weights in one group or another.

What are hyperparameters?

Hyperparameters are values ​​that need to be selected manually and often by trial and error. Among these values ​​are:

• Moment and speed of learning
• The number of hidden layers
• The number of neurons in each layer
• Presence or absence of displacement neurons

In other types of NA, there are additional hyperparameters, but we will not talk about them. Finding the right hyperparameters is very important and will directly affect the convergence of your NA. Understanding whether to use displacement neurons or not is quite simple. The number of hidden layers and neurons in them can be calculated by enumeration based on one simple rule - the more neurons, the more accurate the result and the more exponentially more time you spend on its training. However, it is worth remembering that you should not do NA with 1000 neurons to solve simple problems. But with the choice of the moment and speed of learning, everything is a little more complicated. These hyperparameters will vary, depending on the task and the architecture of the NA. For example, for the XOR solution, the learning rate may be within 0.3 - 0.7, but in the NA which analyzes and predicts the stock price, the learning rate above 0.00001 leads to poor convergence of the NA. It is not worthwhile now to focus your attention on hyperparameters and try to thoroughly understand how to choose them. This will come with experience, but for now I advise you to just experiment and look for examples of solving a particular problem on the web.

What is convergence?

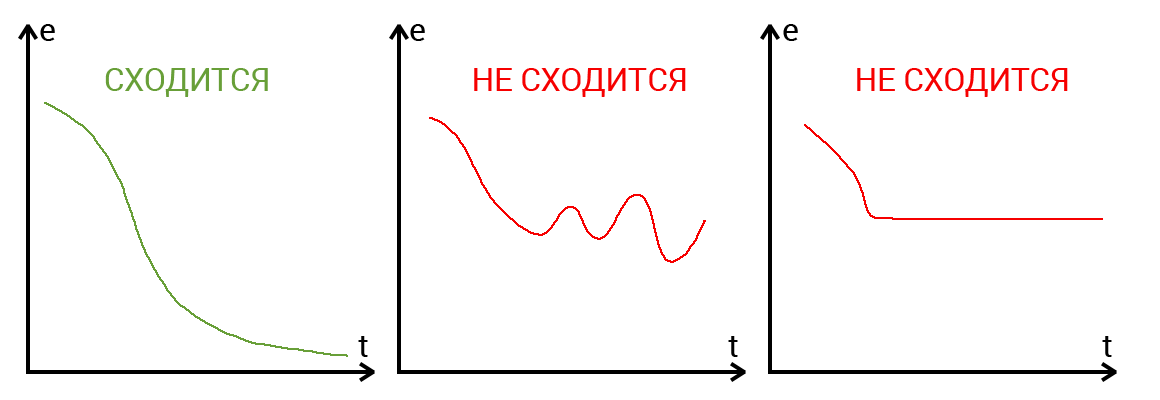
The convergence suggests whether the architecture of the National Assembly is correct and whether the hyper parameters were correctly selected in accordance with the task. Suppose our program displays the error NA at each iteration in the log. If with each iteration the error decreases, then we are on the right track and our NA converges. If the error jumps up - down or freezes at a certain level, then the National Assembly does not converge. In 99% of cases, this is solved by changing the hyperparameters. The remaining 1% will mean that you have an error in the NA architecture. It also happens that convergence is affected by convergence.

What is retraining?

Re-training, as the name implies, is a state of a neural network when it is oversaturated with data. This problem occurs if it takes too long to train the network on the same data. In other words, the network will begin not to learn from the data, but to memorize and “cram” them. Accordingly, when you will be already submitting new data to the input of this NA, then noise may appear in the data obtained, which will affect the accuracy of the result. For example, if we show the NA different photos of apples (only red) and say that this is an apple. Then, when the NA sees a yellow or green apple, it will not be able to determine that it is an apple, as she remembered that all apples should be red. And vice versa, when the NA sees something red and coincides in shape with an apple, for example a peach, she will say that it is an apple. This is the noise. On the graph, the noise will look like this.


It is seen that the graph of the function varies greatly from point to point, which are the output (result) of our NA. Ideally, this graph should be less wavy and straight. To avoid retraining, it is not worth long to train the NA on the same or very similar data. Also, retraining can be caused by a large number of parameters that you apply to the input of the National Assembly or a very complex architecture. Thus, when you notice errors (noise) in the output after the training stage, then you should use one of the regularization methods, but in most cases this will not be necessary.

Conclusion

I hope this article was able to clarify the key points of such a difficult subject as Neural Networks. However, I believe that no matter how many articles you read, it is impossible to master such a complex topic without practice. Therefore, if you are only at the beginning of the journey and want to study this promising and developing industry, then I advise you to start practicing with writing your NA, and afterwards resort to the help of various frameworks and libraries. Also, if you are interested in my method of presenting information and you want me to write articles on other topics related to Machine Learning, then vote in the poll below for the topic that you are interested in. See you in future articles :)