Programming & Music: Buttervo Frequency Filter. Part 3

Hello! You are reading the third part of an article about creating a VST synthesizer in C #. In the previous sections, the SDK and libraries for creating VST plug - ins were considered, the programming of an oscillator and an ADSR envelope for controlling the amplitude of a signal were considered.

In this part, I will tell you how to calculate and code the frequency filter, without which no synthesizer can do. And without equalizer sound processing is inconceivable.

The source code and the use of an equalizer from the NAudio library (a library for working with sound under .NET) will be reviewed.

Attention - there will be a lot of matan - we will calculate the formulas for the filter coefficients.

The source code for the synthesizer I've written is available on GitHub .

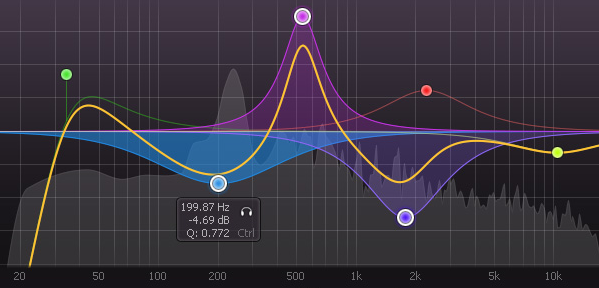
Screenshot VST plug-in equalizer Fab Filter Pro Q

Cycle of articles

We understand and write VSTi synthesizer on C # WPF
ADSR signal envelope
Buttervo Frequency Filter
Delay, Distortion and Parameter Modulation

Equalizer

Often when processing sound we want to change its character / color / timbre. Make the sound more bass, remove the upper frequencies, or vice versa, make the sound "transparent", leaving only the middle and the top. I am sure many people who have not worked with sound processing know what equalizer is - they are acoustic speakers, music centers, tape recorders, music players, etc. An equalizer is a set of filters, each of which changes the amplitude of a signal in its selected frequency band. On household speakers, these are usually 2-3 spins - low frequencies, mid and top, with fixed frequency bands.

There are already 10 pre-defined bands in Winamp EQ.

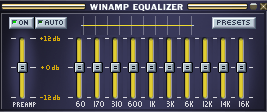
Screenshot Equalizer Player Winamp

In the world of sound processing, there are many equalizer plug-ins, for every taste and color. The Fab Filter Pro Q plug-in (screenshot at the beginning of the article) is a graphic equalizer that allows you to create a large number of bands and edit their parameters.

Each band in the equalizer is, in fact, a frequency filter. Frequency filters change the timbre / frequency characteristics of a signal. In electronics, there are many types and classifications of filters, with the corresponding characteristics and parameters - look Wikipedia .
We will consider and program the simplest filters: low-pass, high-pass and band-pass filters.

Fourier Transform Filtering

In theory, no one bothers you to do a discrete Fourier transform with the signal, process the frequencies and then do the inverse transform.

If you do not think about the implementation of the DFT, then I would call such an approach quite intuitive and easy to program (again, if you take the DFT from any of them and do not code it yourself).

The disadvantages of the approach are, first, the DFT accepts an array of samples as input, the size of which is a power of two. This means that the output signal will be delayed. Secondly, every 512th sample we will produce this algorithm: DFT, signal frequency processing, inverse DFT. This is not a small calculation. Thirdly, there are still minuses and subtleties that adherents of digital signal processing know.

We will not consider the use of DFT, but look at the theory of digital filters; write a filter that processes the values of the samples and has a linear computational complexity depending on the length of the incoming sample array.

Digital filters

Most of the information and the derivation of formulas I took from the book Digital Signal Processing: A Practical Approach - I highly recommend it, it is in the Russian version - Digital Signal Processing. Practical approach , interested will find PDF on the net.

I want to make an important note . The topic of building and calculating a filter is really very complex, it contains a lot of subtleties and nuances, it requires knowledge and understanding of the theory. In this article, I will show how to calculate the Butterwater filter formulas so that the reader has an understanding of where these formulas are derived from. But why exactly such initial formulas, why exactly such replacements can be understood only by immersing ourselves in the deep theory of digital signal processing.

When I started to google the filter code, I immediately found a lot of incomprehensible mathematical code, and I wanted to at least a little bit understand where such calculation formulas come from. Oscillator, envelope, delay - understanding and programming the work of these components seems to me intuitive, but not filters. In this article I want to arouse an interest in digital signal processing) I would be glad if there is a desire to understand this topic more thoroughly.

You need to know (at least a little) terms such as convolution , filter impulse response, filter transfer function .

Approximation of the frequency response of the ideal filter (picture from the Soviet textbook, did not find the source)

The filter changes the signal, "removing" in it the selected frequency. Existing filters are not perfect. Bandwidth is a frequency band that the filter "does not affect" (there is some changes are a feature of the imperfect filter presented). Band of suppression - the band of unwanted frequencies. Frequency decay occurs in the transition band. Naturally, the filter is closer to the “ideal” one by how much less it distorts the bandwidth, how much it suppresses the frequencies in the suppression band and how narrow the transition band is. There are various "approximations" of filters - the Chebyshev, Buttervota filter, and so on - you will find them in books and in the open spaces of the network.

Why filter Buttervota?

It's very simple, the Butterworth frequency response of the filter is as smooth as possible at the passband frequencies - IMHO, the most important thing is not to spoil the signal in the passband.

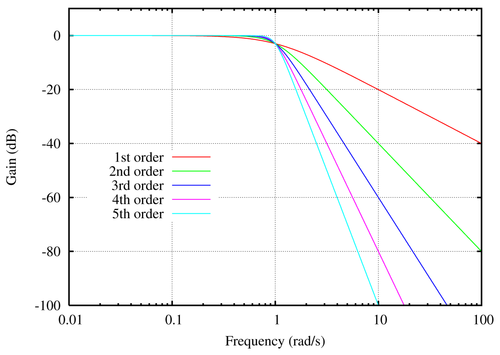
Logarithmic frequency response for Butterworth filters of low frequencies of different orders (screenshot taken from Wikipedia)

The output of the low-pass filter formula

The transfer function for the Butterwater filter on the s-plane is written by the following formulas:

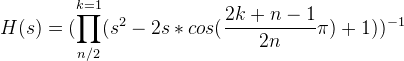with even n and
with odd n

Here n is the order of the filter: the amplitude at the cut-off frequency w is -3n dB, the amplitude-frequency characteristic decays by −6n dB per octave.

To obtain convolution coefficients, one must obtain the transfer function on the z-plane in the form

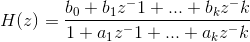
Find the transfer function for the filter of the second order (attenuation by -6 dB per octave), substitute in the formula for H (s) n = 2:

Then the convolution for the filter will look like this:

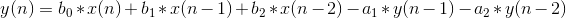
Let us set the cut-off frequency w (at which the signal amplitude will be -3 dB) and Fc - the sampling frequency (number of samples per second), in hertz.

In the formula, one should use denormalized frequencies, i.e. to replace (in the bandpass filter there will be two frequencies w1 and w2, which determine the bandwidth):

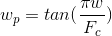
If we want to calculate the low-pass filter, then we need to do a conversion — replace the parameter s in the transfer function:

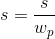
To calculate other types of filters (HF, bandpass, notch) you need to do other replacements. They are discussed in the book Digital Signal Processing. A practical approach in part 8.8.2 and further in the article.

Further, in order to go to the z-plane, we make a replacement:

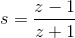
For analytical calculations, I used the Mathematica package.

You need to get the numerator and denominator in the form of polynomials from z. We give the terms of the denominator H (z) to a common denominator. To do this, we find the greatest common divisor (GCD, GCD) of the terms of the denominator and divide into it the numerator and denominator of the original function H (z).

Find the coefficients in powers of the polynomials obtained using the CoefficientList function:

If we do everything honestly, then, by the condition, a0 must be equal to 1 - divide all coefficients by a0 (for coding, we will use the previous formulas without division):

The output of the formula of the filter RF and bandpass filter

The derivation of formulas for the high-pass filter is similar to the low-pass filter with a different conversion:

To output the band-pass filter formulas, a transformation is applied:

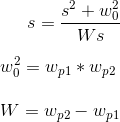
If a replacement is made, then the degree of polynomials in the numerator and denominator H (z) will double (the replacement is s ^ 2), which means that the order of the filter will double. Therefore, we initially use the function H (s) for n = 1:

Programming the Butterwater filter using the formulas obtained

The filter will have 2 parameters: filter type (LF, HF, bandpass) and cut-off frequency w. For a bandpass filter, we will consider the cutoff frequency as the frequency in the middle of the passband. The bandwidth is defined as the frequency interval [w - w / 4, w + w / 4] (you can think of a more complex and logical logarithmic law here, at your discretion).

Suppose that we determined the coefficients b0, b1, b2, a1 and a2 (a0 is equal to 1 by the condition) by the calculated formulas. The filter operation algorithm is reduced to convolution, which is done sequentially for each sample:

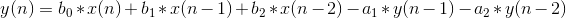
y (n) is the new value of the sample to be calculated. x (n) is the current value of the sample, respectively, y (n-1) and y (n-2) are the previous 2 calculated samples, and x (n-1) and x (n-2) are the previous input values of the samples.

It is necessary to organize the memorization of previous samples. Let's not be wise with cyclic buffers, let's make it simple and clear: two arrays of three elements. Each time we will "push" the new values into this array, sequentially copying the older values of the samples.

We get a simple class:

class BiquadConvolutionTable { public double B0, B1, B2, A1, A2; private readonly double[] _x = new double[3]; private readonly double[] _y = new double[3]; public double Process(double s) { // ""   _x[2] = _x[1]; _x[1] = _x[0]; _x[0] = s; _y[2] = _y[1]; _y[1] = _y[0]; //  _y[0] = B0 * _x[0] + B1 * _x[1] + B2 * _x[2] - A1 * _y[1] - A2 * _y[2]; return _y[0]; } }

Let's write a frame class for the filter (see the synthesizer architecture in the first article ). The class BiquadConvolutionTable works with one signal, i.e. with one channel - mono. Therefore, we need two BiquadConvolutionTable - for the left and right channels.

To apply the filter correctly, you need to apply the function BiquadConvolutionTable.Process for all samples of the incoming sequence and fill the resulting array of samples.

The calculation of the coefficients for the BiquadConvolutionTable will be handled by the CalculateCoefficients function.

 public enum EFilterPass { None, LowPass, HiPass, BandPass } public class ButterworthFilter : SyntageAudioProcessorComponentWithParameters<AudioProcessor>, IProcessor { private readonly BiquadConvolutionTable _tablel; private readonly BiquadConvolutionTable _tabler; public EnumParameter<EFilterPass> FilterType { get; private set; } public FrequencyParameter CutoffFrequency { get; private set; } public ButterworthFilter(AudioProcessor audioProcessor) : base(audioProcessor) { _tablel = new BiquadConvolutionTable(); _tabler = new BiquadConvolutionTable(); } public override IEnumerable<Parameter> CreateParameters(string parameterPrefix) { FilterType = new EnumParameter<EFilterPass>(parameterPrefix + "Pass", "Filter Type", "Filter", false); CutoffFrequency = new FrequencyParameter(parameterPrefix + "Cutoff", "Filter Cutoff Frequency", "Cutoff"); return new List<Parameter> {FilterType, CutoffFrequency}; } public void Process(IAudioStream stream) { if (FilterType.Value == EFilterPass.None) return; var count = Processor.CurrentStreamLenght; var lc = stream.Channels[0]; var rc = stream.Channels[1]; for (int i = 0; i < count; ++i) { var cutoff = CutoffFrequency.Value; CalculateCoefficients(cutoff); var ls = _tablel.Process(lc.Samples[i]); lc.Samples[i] = ls; var rs = _tabler.Process(rc.Samples[i]); rc.Samples[i] = rs; } } private void CalculateCoefficients(double cutoff) { ... } }

The CalculateCoefficients function is called every time in the loop - why? In the next article I will talk about the modulation (change over time) of parameters, and therefore, the cutoff frequency may change, which means that you need to recalculate the coefficients. Of course, in a scrappy way, you need to subscribe to a change in the cutoff frequency and already in the handler calculate the coefficients. But in these articles I will not deal with optimizations, the goal is to code the filter.

It remains to code the CalculateCoefficients function using the calculated formulas for the coefficients.
Recall that you need to use denormal frequencies, i.e. replace:

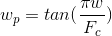
Write off all the formulas for the coefficients b0, b1, b2, a0, a1, a2. After the calculations, all coefficients must be divided by a0 so that a0 becomes equal to 1.

 private double TransformFrequency(double w) { return Math.Tan(Math.PI * w / Processor.SampleRate); } private void CalculateCoefficients(double cutoff) { double b0, b1, b2, a0, a1, a2; switch (FilterType.Value) { case EFilterPass.LowPass: { var w = TransformFrequency(cutoff); a0 = 1 + Math.Sqrt(2) * w + w * w; a1 = -2 + 2 * w * w; a2 = 1 - Math.Sqrt(2) * w + w * w; b0 = w * w; b1 = 2 * w * w; b2 = w * w; } break; case EFilterPass.HiPass: { var w = TransformFrequency(cutoff); a0 = 1 + Math.Sqrt(2) * w + w * w; a1 = -2 + 2 * w * w; a2 = 1 - Math.Sqrt(2) * w + w * w; b0 = 1; b1 = -2; b2 = 1; } break; case EFilterPass.BandPass: { var w = cutoff; var d = w / 4; //     [w * 3 / 4, w * 5 / 4] var w1 = Math.Max(w - d, CutoffFrequency.Min); var w2 = Math.Min(w + d, CutoffFrequency.Max); w1 = TransformFrequency(w1); w2 = TransformFrequency(w2); var w0Sqr = w2 * w1; // w0^2 var wd = w2 - w1; // W a0 = -1 - wd - w0Sqr; a1 = 2 - 2 * w0Sqr; a2 = -1 + wd - w0Sqr; b0 = -wd; b1 = 0; b2 = wd; } break; default: throw new ArgumentOutOfRangeException(); } _tablel.B0 = _tabler.B0 = b0 / a0; _tablel.B1 = _tabler.B1 = b1 / a0; _tablel.B2 = _tabler.B2 = b2 / a0; _tablel.A1 = _tabler.A1 = a1 / a0; _tablel.A2 = _tabler.A2 = a2 / a0; }

Full code of the class ButterworthFilter

 public enum EFilterPass { None, LowPass, HiPass, BandPass } public class ButterworthFilter : SyntageAudioProcessorComponentWithParameters<AudioProcessor>, IProcessor { private class BiquadConvolutionTable { public double B0, B1, B2, A1, A2; private readonly double[] _x = new double[3]; private readonly double[] _y = new double[3]; public double Process(double s) { // ""   _x[2] = _x[1]; _x[1] = _x[0]; _x[0] = s; _y[2] = _y[1]; _y[1] = _y[0]; //  _y[0] = B0 * _x[0] + B1 * _x[1] + B2 * _x[2] - A1 * _y[1] - A2 * _y[2]; return _y[0]; } } private readonly BiquadConvolutionTable _tablel; private readonly BiquadConvolutionTable _tabler; public EnumParameter<EFilterPass> FilterType { get; private set; } public FrequencyParameter CutoffFrequency { get; private set; } public ButterworthFilter(AudioProcessor audioProcessor) : base(audioProcessor) { _tablel = new BiquadConvolutionTable(); _tabler = new BiquadConvolutionTable(); } public override IEnumerable<Parameter> CreateParameters(string parameterPrefix) { FilterType = new EnumParameter<EFilterPass>(parameterPrefix + "Pass", "Filter Type", "Filter", false); CutoffFrequency = new FrequencyParameter(parameterPrefix + "Cutoff", "Filter Cutoff Frequency", "Cutoff"); return new List<Parameter> {FilterType, CutoffFrequency}; } public void Process(IAudioStream stream) { if (FilterType.Value == EFilterPass.None) return; var count = Processor.CurrentStreamLenght; var lc = stream.Channels[0]; var rc = stream.Channels[1]; for (int i = 0; i < count; ++i) { var cutoff = CutoffFrequency.Value; CalculateCoefficients(cutoff); var ls = _tablel.Process(lc.Samples[i]); lc.Samples[i] = ls; var rs = _tabler.Process(rc.Samples[i]); rc.Samples[i] = rs; } } private double TransformFrequency(double w) { return Math.Tan(Math.PI * w / Processor.SampleRate); } private void CalculateCoefficients(double cutoff) { double b0, b1, b2, a0, a1, a2; switch (FilterType.Value) { case EFilterPass.LowPass: { var w = TransformFrequency(cutoff); a0 = 1 + Math.Sqrt(2) * w + w * w; a1 = -2 + 2 * w * w; a2 = 1 - Math.Sqrt(2) * w + w * w; b0 = w * w; b1 = 2 * w * w; b2 = w * w; } break; case EFilterPass.HiPass: { var w = TransformFrequency(cutoff); a0 = 1 + Math.Sqrt(2) * w + w * w; a1 = -2 + 2 * w * w; a2 = 1 - Math.Sqrt(2) * w + w * w; b0 = 1; b1 = -2; b2 = 1; } break; case EFilterPass.BandPass: { var w = cutoff; var d = w / 4; //     [w * 3 / 4, w * 5 / 4] var w1 = Math.Max(w - d, CutoffFrequency.Min); var w2 = Math.Min(w + d, CutoffFrequency.Max); w1 = TransformFrequency(w1); w2 = TransformFrequency(w2); var w0Sqr = w2 * w1; // w0^2 var wd = w2 - w1; // W a0 = -1 - wd - w0Sqr; a1 = 2 - 2 * w0Sqr; a2 = -1 + wd - w0Sqr; b0 = -wd; b1 = 0; b2 = wd; } break; default: throw new ArgumentOutOfRangeException(); } _tablel.B0 = _tabler.B0 = b0 / a0; _tablel.B1 = _tabler.B1 = b1 / a0; _tablel.B2 = _tabler.B2 = b2 / a0; _tablel.A1 = _tabler.A1 = a1 / a0; _tablel.A2 = _tabler.A2 = a2 / a0; } }

Band equalizer in NAudio library

For working with sound, sound files of various formats on .NET there is a good NAudio library.

It contains the NAudio.Dsp namespace with functionality for filtering, convolution , gate , envelope , FFT, and other interesting pieces.

Consider the Equalizer class (from examples, the NAudioWpfDemo.EqualizationDemo namespace), which allows equalization of the signal. The class implements ISampleProvider, which, in the Read (float [] buffer, int offset, int count) function, processes (changes) the buffer samples array.

The constructor accepts an array of EqualizerBand structures that describe the equalizer bands:

 class EqualizerBand { public float Frequency { get; set; } public float Gain { get; set; } public float Bandwidth { get; set; } }

Here Frequency is the center frequency of the band with the parameter Q (Bandwidth, filter Q ), with gain Gain dB.

If you look at the implementation, then each band EqualizerBand corresponds to the class BiQuadFilter which is used as a bandpass (Peaking) filter. All filters change the signal used in series.

The EqualizerBand class is a implementation of the Butterwater filter, with a large selection of filter types and parameters. If you look at the implementation, you can see similar formulas and coefficients.

An example of using the Equalizer class can be found in the NAudioWpfDemo project in the EqualizationDemoViewModel class.

Programs for calculating filters

The progenitor of digital filters were analog filters. The theory for analog circuits and analog signal processing later developed into the theory of digital signal processing.

For the considered Butterwater filter and the calculated formulas for the coefficients, an analog circuit can be assembled.

There are many programs for calculating and constructing schemes, parameters of elements for them, convolution coefficients of various filters.
You can google by "filter calculation software".

Iowa Hills Software RF Filter Designer

In the next article I will talk about the effect of delay , distortion and parameter modulation.

All good! Good luck in programming!

Bibliography

Do not forget to look at the lists of articles and books in previous articles.

Source: https://habr.com/ru/post/313062/

All Articles