Create and estimate the number of sudoku
From school age I liked sudoku. It helped to while away the time to go to school (and even now I play on the way to work). Soon I was able to get my grandmother on the sudoku, but the problem was that she could not play on the electronic device. Because the idea came to mind to make your sudoku, which can be printed.
How to make your own sudoku generator and how many different options can be and will be discussed under the cut.

I will implement everything on Pascal, as it was closest to the mouse at the time of this writing. However, everything can be implemented in other languages.
')
The first method, which we consider, will be the replacement of some figures by others in the original Sudoku example. For the original version, we take the following table.
The essence of the method is to compare each digit with another digit and thereby change the whole sudoku in its entirety.
To do this, we use a one-dimensional matrix with indices from 1 to 9 and fill in at the very beginning all the cells in accordance with their indices. And then we will take two random cells and change their values between themselves. Note that having done this operation an odd number of times we will not get the original version of filling the matrix (proof is provided to the reader). For those who doubt at the end of the program, one million sudoku matrices are generated and their coincidence with the initial one is evaluated.
Having calculated, we get 9! The options are 362,880 different combinations.
This is the way that was still on Habré a couple of years ago. Read details here .
And here I will give a brief squeeze:
It is also worth noting that an odd number of permutations guarantees a difference from the original version.
Therefore, we first realize the exchange of rows and the exchange of columns in the Sudoku matrix. Also, to simplify the code, insert the function of replacing numbers alphabetically (the method described earlier)
Having calculated, we get that when replacing only one triple of columns / rows, you can increase the number of variants by 6 times for every triple (6 * 6 * 6 for the columns and the same for the rows, totaling 46,656 variants).
And we will also write a separate function that will compare two sudoku character by character and return true / false if they match / do not match.
It is necessary to explain why the resulting two numbers can be multiplied. When replacing strings, we will not get the same option as when replacing numbers, because otherwise we will get another replacement alphabet (having considered the last replacement of strings, we can find a contradiction).
Therefore, this algorithm allows you to create up to 362,880 * 46,656 or 16,930,529,280 options.
The article does not describe all transformations with a sudoku table (replacing a triple of columns / rows, transposing, etc.), which proves that the number of sudoku variants is even greater.
How to make your own sudoku generator and how many different options can be and will be discussed under the cut.

I will implement everything on Pascal, as it was closest to the mouse at the time of this writing. However, everything can be implemented in other languages.
')
▍ Method one. Alphabetical replacement.
The first method, which we consider, will be the replacement of some figures by others in the original Sudoku example. For the original version, we take the following table.
Picture table

The essence of the method is to compare each digit with another digit and thereby change the whole sudoku in its entirety.
To do this, we use a one-dimensional matrix with indices from 1 to 9 and fill in at the very beginning all the cells in accordance with their indices. And then we will take two random cells and change their values between themselves. Note that having done this operation an odd number of times we will not get the original version of filling the matrix (proof is provided to the reader). For those who doubt at the end of the program, one million sudoku matrices are generated and their coincidence with the initial one is evaluated.
Explanatory image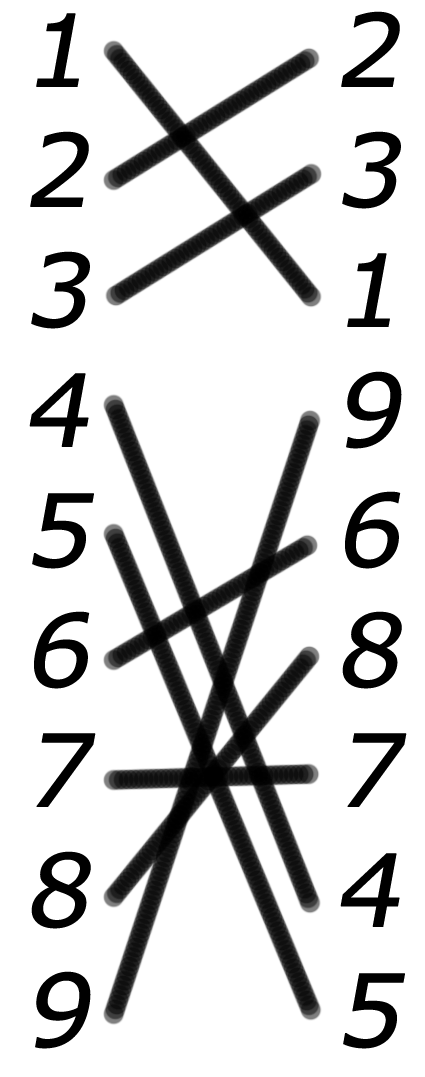

Pascal code
type rec = record // replacement alphabet
num: array [1..9] of integer;
constructor Create ();
var i: integer;
begin
for i: = 1 to 9 do
num [i]: = i;
end;
procedure rand (); // random exchange of two numbers in the alphabet
var i, j, k: integer;
begin
i: = random (1.9);
j: = i;
while (i = j) do j: = random (1.9);
k: = num [i];
num [i]: = num [j];
num [j]: = k;
end;
procedure wr (); // display the alphabet on the screen
var i: integer;
begin
for i: = 1 to 9 do
write (num [i] + '');
writeln;
end;
end;
num: array [1..9] of integer;
constructor Create ();
var i: integer;
begin
for i: = 1 to 9 do
num [i]: = i;
end;
procedure rand (); // random exchange of two numbers in the alphabet
var i, j, k: integer;
begin
i: = random (1.9);
j: = i;
while (i = j) do j: = random (1.9);
k: = num [i];
num [i]: = num [j];
num [j]: = k;
end;
procedure wr (); // display the alphabet on the screen
var i: integer;
begin
for i: = 1 to 9 do
write (num [i] + '');
writeln;
end;
end;
Having calculated, we get 9! The options are 362,880 different combinations.
▍ Method two. Matrix permutations.
This is the way that was still on Habré a couple of years ago. Read details here .
And here I will give a brief squeeze:
You can change the rows / columns in triples, as shown in the pictures.



It is also worth noting that an odd number of permutations guarantees a difference from the original version.
Therefore, we first realize the exchange of rows and the exchange of columns in the Sudoku matrix. Also, to simplify the code, insert the function of replacing numbers alphabetically (the method described earlier)
Pascal code
type sudoku = record // sudoku table
num: array [1..9] of array [1..9] of integer;
constructor Create (); // range from 1 to 9 shifted cyclically so that the table complies with the Sudoku rules
begin
num [1] [1]: = 1; num [1] [2]: = 2; num [1] [3]: = 3; num [1] [4]: = 4; num [1] [5]: = 5; num [1] [6]: = 6; num [1] [7]: = 7; num [1] [8]: = 8; num [1] [9]: = 9;
num [2] [1]: = 4; num [2] [2]: = 5; num [2] [3]: = 6; num [2] [4]: = 7; num [2] [5]: = 8; num [2] [6]: = 9; num [2] [7]: = 1; num [2] [8]: = 2; num [2] [9]: = 3;
num [3] [1]: = 7; num [3] [2]: = 8; num [3] [3]: = 9; num [3] [4]: = 1; num [3] [5]: = 2; num [3] [6]: = 3; num [3] [7]: = 4; num [3] [8]: = 5; num [3] [9]: = 6;
num [4] [1]: = 2; num [4] [2]: = 3; num [4] [3]: = 4; num [4] [4]: = 5; num [4] [5]: = 6; num [4] [6]: = 7; num [4] [7]: = 8; num [4] [8]: = 9; num [4] [9]: = 1;
num [5] [1]: = 5; num [5] [2]: = 6; num [5] [3]: = 7; num [5] [4]: = 8; num [5] [5]: = 9; num [5] [6]: = 1; num [5] [7]: = 2; num [5] [8]: = 3; num [5] [9]: = 4;
num [6] [1]: = 8; num [6] [2]: = 9; num [6] [3]: = 1; num [6] [4]: = 2; num [6] [5]: = 3; num [6] [6]: = 4; num [6] [7]: = 5; num [6] [8]: = 6; num [6] [9]: = 7;
num [7] [1]: = 3; num [7] [2]: = 4; num [7] [3]: = 5; num [7] [4]: = 6; num [7] [5]: = 7; num [7] [6]: = 8; num [7] [7]: = 9; num [7] [8]: = 1; num [7] [9]: = 2;
num [8] [1]: = 6; num [8] [2]: = 7; num [8] [3]: = 8; num [8] [4]: = 9; num [8] [5]: = 1; num [8] [6]: = 2; num [8] [7]: = 3; num [8] [8]: = 4; num [8] [9]: = 5;
num [9] [1]: = 9; num [9] [2]: = 1; num [9] [3]: = 2; num [9] [4]: = 3; num [9] [5]: = 4; num [9] [6]: = 5; num [9] [7]: = 6; num [9] [8]: = 7; num [9] [9]: = 8;
end;
procedure change (alf: rec); // alphabetic replacement
var i, j: integer;
begin
for i: = 1 to 9 do
for j: = 1 to 9 do
num [i] [j]: = alf.num [(num [i] [j])];
end;
procedure swip_row (); // swap rows
var i, j, k, r: integer;
begin
i: = random (1.9);
j: = i;
while (j = i) do j: = random (3 * ((i-1 + 3) div 3-1) +1.3 * ((i-1 + 3) div 3-1) +3);
for r: = 1 to 9 do
begin
k: = num [i] [r];
num [i] [r]: = num [j] [r];
num [j] [r]: = k;
end;
end;
procedure swip_line (); // swap columns
var i, j, k, r: integer;
begin
i: = random (1.9);
j: = i;
while (j = i) do j: = random (3 * ((i-1 + 3) div 3-1) +1.3 * ((i-1 + 3) div 3-1) +3);
for r: = 1 to 9 do
begin
k: = num [r] [i];
num [r] [i]: = num [r] [j];
num [r] [j]: = k;
end;
end;
procedure wr (); // display
var i, j: integer;
begin
for i: = 1 to 9 do
begin
for j: = 1 to 9 do
write (num [i] [j], '');
writeln;
end;
writeln;
end;
end;
num: array [1..9] of array [1..9] of integer;
constructor Create (); // range from 1 to 9 shifted cyclically so that the table complies with the Sudoku rules
begin
num [1] [1]: = 1; num [1] [2]: = 2; num [1] [3]: = 3; num [1] [4]: = 4; num [1] [5]: = 5; num [1] [6]: = 6; num [1] [7]: = 7; num [1] [8]: = 8; num [1] [9]: = 9;
num [2] [1]: = 4; num [2] [2]: = 5; num [2] [3]: = 6; num [2] [4]: = 7; num [2] [5]: = 8; num [2] [6]: = 9; num [2] [7]: = 1; num [2] [8]: = 2; num [2] [9]: = 3;
num [3] [1]: = 7; num [3] [2]: = 8; num [3] [3]: = 9; num [3] [4]: = 1; num [3] [5]: = 2; num [3] [6]: = 3; num [3] [7]: = 4; num [3] [8]: = 5; num [3] [9]: = 6;
num [4] [1]: = 2; num [4] [2]: = 3; num [4] [3]: = 4; num [4] [4]: = 5; num [4] [5]: = 6; num [4] [6]: = 7; num [4] [7]: = 8; num [4] [8]: = 9; num [4] [9]: = 1;
num [5] [1]: = 5; num [5] [2]: = 6; num [5] [3]: = 7; num [5] [4]: = 8; num [5] [5]: = 9; num [5] [6]: = 1; num [5] [7]: = 2; num [5] [8]: = 3; num [5] [9]: = 4;
num [6] [1]: = 8; num [6] [2]: = 9; num [6] [3]: = 1; num [6] [4]: = 2; num [6] [5]: = 3; num [6] [6]: = 4; num [6] [7]: = 5; num [6] [8]: = 6; num [6] [9]: = 7;
num [7] [1]: = 3; num [7] [2]: = 4; num [7] [3]: = 5; num [7] [4]: = 6; num [7] [5]: = 7; num [7] [6]: = 8; num [7] [7]: = 9; num [7] [8]: = 1; num [7] [9]: = 2;
num [8] [1]: = 6; num [8] [2]: = 7; num [8] [3]: = 8; num [8] [4]: = 9; num [8] [5]: = 1; num [8] [6]: = 2; num [8] [7]: = 3; num [8] [8]: = 4; num [8] [9]: = 5;
num [9] [1]: = 9; num [9] [2]: = 1; num [9] [3]: = 2; num [9] [4]: = 3; num [9] [5]: = 4; num [9] [6]: = 5; num [9] [7]: = 6; num [9] [8]: = 7; num [9] [9]: = 8;
end;
procedure change (alf: rec); // alphabetic replacement
var i, j: integer;
begin
for i: = 1 to 9 do
for j: = 1 to 9 do
num [i] [j]: = alf.num [(num [i] [j])];
end;
procedure swip_row (); // swap rows
var i, j, k, r: integer;
begin
i: = random (1.9);
j: = i;
while (j = i) do j: = random (3 * ((i-1 + 3) div 3-1) +1.3 * ((i-1 + 3) div 3-1) +3);
for r: = 1 to 9 do
begin
k: = num [i] [r];
num [i] [r]: = num [j] [r];
num [j] [r]: = k;
end;
end;
procedure swip_line (); // swap columns
var i, j, k, r: integer;
begin
i: = random (1.9);
j: = i;
while (j = i) do j: = random (3 * ((i-1 + 3) div 3-1) +1.3 * ((i-1 + 3) div 3-1) +3);
for r: = 1 to 9 do
begin
k: = num [r] [i];
num [r] [i]: = num [r] [j];
num [r] [j]: = k;
end;
end;
procedure wr (); // display
var i, j: integer;
begin
for i: = 1 to 9 do
begin
for j: = 1 to 9 do
write (num [i] [j], '');
writeln;
end;
writeln;
end;
end;
Having calculated, we get that when replacing only one triple of columns / rows, you can increase the number of variants by 6 times for every triple (6 * 6 * 6 for the columns and the same for the rows, totaling 46,656 variants).
And we will also write a separate function that will compare two sudoku character by character and return true / false if they match / do not match.
Pascal code
function compl (s1, s2: sudoku): boolean; // comparison of two sudoku tables
var i, j: integer; flag: boolean;
begin
flag: = true;
for i: = 1 to 9 do
for j: = 1 to 9 do
if (s1.num [i] [j] <> s2.num [i] [j]) then flag: = false;
compl: = flag;
end;
var
a: rec;
nw, was: sudoku;
i: integer;
t, n: integer;
cor: integer;
begin
// Calculate the probability of sudoku coincidence after replacing the alphabet and the original version
cor: = 0;
for t: = 1 to 1000000 do
begin
nw: = new sudoku ();
was: = new sudoku ();
a: = new rec ();
//General remark. With an odd number of permutations, the initial situation is impossible
// for 6 permutations, you can mix all three columns / rows
for i: = 1 to 7 do nw.swip_row (); // 6 * 3 options
for i: = 1 to 7 do nw.swip_line (); // 6 * 3 options
// for 8 paired permutations, you can get any combination of 9 digits.
for i: = 1 to 9 do a.rand (); // 9! options
// Estimated number of choices 117 573 120
nw.change (a);
if (compl (nw, was)) then cor: = cor + 1;
end;
writeln ((cor / 1000000) * 100, '%');
nw.wr ();
end.
var i, j: integer; flag: boolean;
begin
flag: = true;
for i: = 1 to 9 do
for j: = 1 to 9 do
if (s1.num [i] [j] <> s2.num [i] [j]) then flag: = false;
compl: = flag;
end;
var
a: rec;
nw, was: sudoku;
i: integer;
t, n: integer;
cor: integer;
begin
// Calculate the probability of sudoku coincidence after replacing the alphabet and the original version
cor: = 0;
for t: = 1 to 1000000 do
begin
nw: = new sudoku ();
was: = new sudoku ();
a: = new rec ();
//General remark. With an odd number of permutations, the initial situation is impossible
// for 6 permutations, you can mix all three columns / rows
for i: = 1 to 7 do nw.swip_row (); // 6 * 3 options
for i: = 1 to 7 do nw.swip_line (); // 6 * 3 options
// for 8 paired permutations, you can get any combination of 9 digits.
for i: = 1 to 9 do a.rand (); // 9! options
// Estimated number of choices 117 573 120
nw.change (a);
if (compl (nw, was)) then cor: = cor + 1;
end;
writeln ((cor / 1000000) * 100, '%');
nw.wr ();
end.
▍In the conclusion of calculations
It is necessary to explain why the resulting two numbers can be multiplied. When replacing strings, we will not get the same option as when replacing numbers, because otherwise we will get another replacement alphabet (having considered the last replacement of strings, we can find a contradiction).
Therefore, this algorithm allows you to create up to 362,880 * 46,656 or 16,930,529,280 options.
The article does not describe all transformations with a sudoku table (replacing a triple of columns / rows, transposing, etc.), which proves that the number of sudoku variants is even greater.
Source: https://habr.com/ru/post/312822/
All Articles