NSCO algorithm (Ho-Kashyap algorithm)
Often, while working with neural networks, we are faced with the task of constructing linear decision functions (LRF) to separate the classes containing our images.
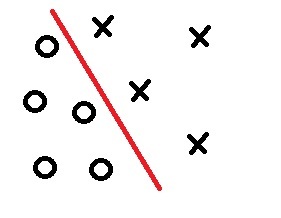
Figure 1. The two-dimensional case.
One of the methods to solve our problem is the algorithm of the smallest mean-square error (NSCO algorithm).
')
This algorithm is of interest not only in the fact that it helps build the LRF we need, but in the case of a situation where classes are linearly inseparable, we can build LRF where the error of incorrect classification tends to a minimum.

Figure 2. Linearly Inseparable Classes
Next we list the source data:
 - class designation (i - class number)
- class designation (i - class number)
 - training set
- training set
 - labels (the class number to which the image belongs
- labels (the class number to which the image belongs 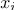 )
)
 - learning rate (arbitrary value)
- learning rate (arbitrary value)
This information is more than enough for us to build LRF.
We proceed directly to the algorithm itself.
a) translate into the system
into the system  where
where  equals
equals  which has an image class assigned at the end
which has an image class assigned at the end
For example:
Let the image be given .
.
Then
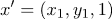 , if a
, if a  from class 1
from class 1
 , if a
, if a  from 2 class
from 2 class
b) build the matrix the dimension of Nx3 which consists of our vectors
the dimension of Nx3 which consists of our vectors 
c) build
d) we consider Where
Where 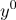 arbitrary vector (single by default)
arbitrary vector (single by default)
d) (iteration number)
(iteration number)
Check the break condition:
If a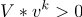 then "STOP"
then "STOP"
otherwise, go to step 3
but)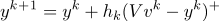 (where + is the Heaviside function)
(where + is the Heaviside function)
For example (Heaviside function):
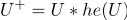
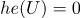 (if a
(if a 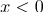 )
)
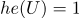 (if a
(if a 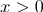 or
or  )
)
After counting, change the iteration number:
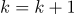
b) go to step 2

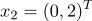
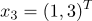
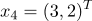
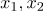 belong to class 1
belong to class 1 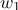
 belong to class 2
belong to class 2 
but)




b)

at)

d)
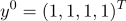
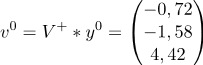
d)
 because all items
because all items 
 "STOP"
"STOP"
The algorithm has been completed, and now we can calculate our LRF.

Thanks parpalak for the online editor.
Thanks for attention.

Figure 1. The two-dimensional case.
One of the methods to solve our problem is the algorithm of the smallest mean-square error (NSCO algorithm).
')
This algorithm is of interest not only in the fact that it helps build the LRF we need, but in the case of a situation where classes are linearly inseparable, we can build LRF where the error of incorrect classification tends to a minimum.

Figure 2. Linearly Inseparable Classes
Next we list the source data:
 - class designation (i - class number)
- class designation (i - class number) - training set
- training set - labels (the class number to which the image belongs
- labels (the class number to which the image belongs 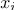 )
) - learning rate (arbitrary value)
- learning rate (arbitrary value)This information is more than enough for us to build LRF.
We proceed directly to the algorithm itself.
Algorithm
1 step
a) translate
 into the system
into the system  where
where  equals
equals  which has an image class assigned at the end
which has an image class assigned at the endFor example:
Let the image be given
 .
.Then
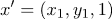 , if a
, if a  from class 1
from class 1 , if a
, if a  from 2 class
from 2 classb) build the matrix
 the dimension of Nx3 which consists of our vectors
the dimension of Nx3 which consists of our vectors 
c) build

d) we consider
 Where
Where 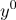 arbitrary vector (single by default)
arbitrary vector (single by default)d)
 (iteration number)
(iteration number)2 step
Check the break condition:
If a
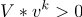 then "STOP"
then "STOP"otherwise, go to step 3
3 step
but)
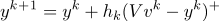 (where + is the Heaviside function)
(where + is the Heaviside function)For example (Heaviside function):
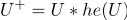
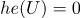 (if a
(if a 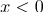 )
)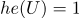 (if a
(if a 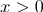 or
or  )
)After counting, change the iteration number:
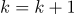
b) go to step 2
An example of the operation of the NSCO algorithm

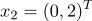
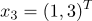
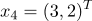
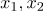 belong to class 1
belong to class 1 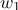
 belong to class 2
belong to class 2 
but)




b)

at)

d)
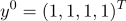
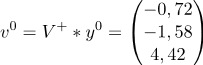
d)

 because all items
because all items 
 "STOP"
"STOP"The algorithm has been completed, and now we can calculate our LRF.

Thanks parpalak for the online editor.
Thanks for attention.
Source: https://habr.com/ru/post/312600/
All Articles