Elimination of perspective distortions and extension of curved lines in photos of book spreads
Last time, in the article “Searching the spine line in photos of book spreads,” we promised to talk about what happens with a photo of a book spread after this, namely, about eliminating perspective distortions and unbending curved lines of text. Without this, getting quality OCR results is almost impossible.
So, we believe that we have already found the line of the spine in the photo, we will use this knowledge to determine the vanish points for the vanishing point pages. Vanish points are the points of convergence of parallel lines in the perspective projection of the book onto the image plane. Both of them should be located on the continuation of this line, but for each of the pages the position of the point may be different. This is schematically shown in the following illustration (in fact, it is a log for debugging). The root line is highlighted in red, the lines intersecting at the Vanish points are green.
')
As a rule, the Vanish points of two pages are not far from each other, but the given example shows that this is not always the case: for the left page of this reversal, the green lines converge very weakly and the Vanish point lies far below, and for the right page it is up close to the edge of the image.
How can I find these lines in the image? Again, the Hough transform comes to the rescue, only the image we have to prepare accordingly. We will try to highlight the boundaries of the text blocks in the image as simple as possible. To do this, perform the following simple steps:
1) Binarization;
2) Normalization of the image size, for example, up to 800 pixels on the long side;
3) Morphological build-up (dilation, r = 6);
4) Morphological gradient (r = 1).
If we apply the fast Hough transform to the resulting image, we get:
On it, several local maxima are clearly distinguishable, corresponding to the borders of pages and text blocks. The root line divides these sets into two (let's call them “left” and “right”, respectively), and each of them is well described by a line in the Hough space. As you know, the lines in the Hough space correspond to points in the image space. These are the desired Vanish points.
To search for lines in Hough space, it is proposed to first select local maxima using the non-maximum suppression algorithm. We reject all maxima weaker than 0.2 of the highest. In principle, the noise can be filtered in a different way; here it is important to leave only the points corresponding to sufficiently long contours in the gradient image. The group of maxima from the neighborhood of the point corresponding to the line of the root (in the figure at the beginning of the article it is highlighted in red), we average and add the center of this cluster to the “left” and “right” sets of points with increased weight. We use the least squares method ( OLS ) to search for lines that describe our sets of points (in the figure they are highlighted in green). Thus, we have obtained Vanish points in the space of the original image. Unfortunately, depicting them on it will not work, since they lie far beyond its borders. Knowing the positions of these points, we drew virtual lines intersecting in them - we look again at the first picture, they are highlighted in green there.
Now we can straighten the original image, correcting the vertical perspective on it. We construct virtual quadrangles of pages on the original image. We need to somehow set the coordinates of the four corners of the document, according to which we can construct a projective transformation. It is worth noting that such a construction is not unique, based on the nature of the observed things, we chose the following option: we consider that our quadrilaterals are trapeziums, their bases are perpendicular to the spine line, which is one of the lateral sides, and the other lateral side passes through the vanish point. and the middle of the side of the image. So, on the one hand, we do not cut off too much from the picture, and on the other hand, we do not make our quadrilaterals too large. Here, for example, another picture, but the principle does not change:
Of course, it is possible to set the bases of the trapezoids higher or lower, to move the outer sides outwards or inwards and to obtain other projective transformations, but at this stage it is only important for us that the spine becomes vertical and the lines are of the same length. We apply the obtained projective transformations independently for each of the pages, we get:
The vertical perspective can be considered corrected. We now turn to the extension of the curved lines.
We select oblique "fragments" of words in the image (and for this, the picture is binarized, connected components stand out on it, a graph is constructed describing their mutual position, the words are pre-assembled). The color shows the angle of the fragment: if <0 is green, if> 0 is red, equal to 0 (rounded to 1 degree), blue.
By "fragment" we mean here "connected in a word" connected components. It can correspond to both the word as a whole, and some fragment of the word, it is only the result of a preliminary analysis, not claiming to be true. You can see that far from all the words have stood out, but for building a page model this will be enough.
Use the following page model:
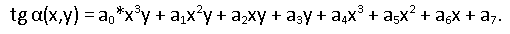
What does this formula tell us? The tangent of the local angle of the rows is a third-degree polynomial horizontally and one degree vertically (here and below we use the usual Cartesian coordinates on the plane). In fact, if we assume that page distortions in space are cylindrical (the sheet bending radius depends only on the x coordinate), then the dependence of the angle of inclination along the vertical when projected onto the image plane will be linear. In the horizontal direction, we believe that a third-degree polynomial will describe the varying angle of inclination with sufficient accuracy. Of course, we tried polynomials of smaller and larger degrees. In general, the choice of model is somewhat arbitrary, it is important that it describes the observed angles well enough. Where do we get them from? Of those very oblique fragments of words. We have a sample of data on the local angles of inclination of the lines for a page; each fragment has its center coordinates and the value of the angle of inclination, which we determine from a set of glued connected components.
We use the usual OLS to find the vector of parameters
. Next, we will filter out the emissions, because we could, by mistake instead of a word fragment, select somewhere else (we had a rough, preliminary analysis).
Here
- the angle value calculated by the model at a point with the coordinates of the center of the i -th fragment, 
- the value of the angle of inclination of the fragment itself (initial data), the values of the angles are given in radians. If, as a result of filtering, we still have a sufficient number of fragments described by the model with a given error, we can refine it by applying the OLS to the remaining data. Thus we get a preliminary model of the page. It describes quite well the curved lines in those parts of the image where we had allocated a sufficient number of word fragments, but in the spine area the solution is inaccurate. If we use it to straighten lines, this area will be distorted.
Let's try using our model to “trace” the lines to the end. The centers of the word fragments will serve as priming for the tracking algorithm.
Prepare an image for tracing curved lines:
- binarization
- horizontal closure (row assembly),
- horizontal opening (getting rid of the title, remote elements),
- Gaussian anti-aliasing (slightly blur the lines vertically).
Closing and opening is performed with a window of width R = w / 100 , where w is the width of the image. Smoothing is performed with σ = h / 400 , where h is the height of the image.
We trace the lines, starting from the center of each fragment of the word in both directions.
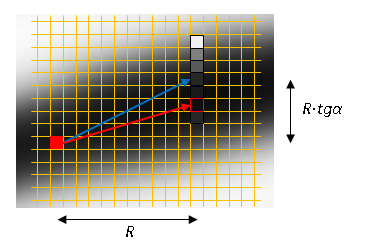
Each time we shift by a fixed step R horizontally and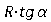
vertically. The angle is determined by the model. Make a local maximum search in a vertical column with a height of ± 3 pixels. We continue the process from the revised position. The stopping criterion is the absence of a local maximum or the maximum value does not exceed the noise threshold (T = 30) .
As a result of tracking, we get much more data - segments with a refined value of the angle of inclination. We specify our model using this data.
Using the map of angles obtained from the model, we construct a map of local displacements. We take into account the angle of the horizontal perspective at the current point:
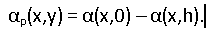
Offset at any point multiplied by
. This allows you to "stretch" the letters in the spine.
► ► ► 
We receive the image which can already be submitted on input of OCR. To build a pleasing to the eye pictures will have to work. We would like to get something like this:
How to do this (of course, automatically), we offer to reflect on the readers. In conclusion, we note that this algorithm has already found application in the ABBYY FineScanner mobile application, which is now able to process photos of book spreads.
So, we believe that we have already found the line of the spine in the photo, we will use this knowledge to determine the vanish points for the vanishing point pages. Vanish points are the points of convergence of parallel lines in the perspective projection of the book onto the image plane. Both of them should be located on the continuation of this line, but for each of the pages the position of the point may be different. This is schematically shown in the following illustration (in fact, it is a log for debugging). The root line is highlighted in red, the lines intersecting at the Vanish points are green.
')
As a rule, the Vanish points of two pages are not far from each other, but the given example shows that this is not always the case: for the left page of this reversal, the green lines converge very weakly and the Vanish point lies far below, and for the right page it is up close to the edge of the image.
How can I find these lines in the image? Again, the Hough transform comes to the rescue, only the image we have to prepare accordingly. We will try to highlight the boundaries of the text blocks in the image as simple as possible. To do this, perform the following simple steps:
1) Binarization;
2) Normalization of the image size, for example, up to 800 pixels on the long side;
3) Morphological build-up (dilation, r = 6);
4) Morphological gradient (r = 1).
If we apply the fast Hough transform to the resulting image, we get:
On it, several local maxima are clearly distinguishable, corresponding to the borders of pages and text blocks. The root line divides these sets into two (let's call them “left” and “right”, respectively), and each of them is well described by a line in the Hough space. As you know, the lines in the Hough space correspond to points in the image space. These are the desired Vanish points.
To search for lines in Hough space, it is proposed to first select local maxima using the non-maximum suppression algorithm. We reject all maxima weaker than 0.2 of the highest. In principle, the noise can be filtered in a different way; here it is important to leave only the points corresponding to sufficiently long contours in the gradient image. The group of maxima from the neighborhood of the point corresponding to the line of the root (in the figure at the beginning of the article it is highlighted in red), we average and add the center of this cluster to the “left” and “right” sets of points with increased weight. We use the least squares method ( OLS ) to search for lines that describe our sets of points (in the figure they are highlighted in green). Thus, we have obtained Vanish points in the space of the original image. Unfortunately, depicting them on it will not work, since they lie far beyond its borders. Knowing the positions of these points, we drew virtual lines intersecting in them - we look again at the first picture, they are highlighted in green there.
Now we can straighten the original image, correcting the vertical perspective on it. We construct virtual quadrangles of pages on the original image. We need to somehow set the coordinates of the four corners of the document, according to which we can construct a projective transformation. It is worth noting that such a construction is not unique, based on the nature of the observed things, we chose the following option: we consider that our quadrilaterals are trapeziums, their bases are perpendicular to the spine line, which is one of the lateral sides, and the other lateral side passes through the vanish point. and the middle of the side of the image. So, on the one hand, we do not cut off too much from the picture, and on the other hand, we do not make our quadrilaterals too large. Here, for example, another picture, but the principle does not change:
Of course, it is possible to set the bases of the trapezoids higher or lower, to move the outer sides outwards or inwards and to obtain other projective transformations, but at this stage it is only important for us that the spine becomes vertical and the lines are of the same length. We apply the obtained projective transformations independently for each of the pages, we get:
The vertical perspective can be considered corrected. We now turn to the extension of the curved lines.
We select oblique "fragments" of words in the image (and for this, the picture is binarized, connected components stand out on it, a graph is constructed describing their mutual position, the words are pre-assembled). The color shows the angle of the fragment: if <0 is green, if> 0 is red, equal to 0 (rounded to 1 degree), blue.
By "fragment" we mean here "connected in a word" connected components. It can correspond to both the word as a whole, and some fragment of the word, it is only the result of a preliminary analysis, not claiming to be true. You can see that far from all the words have stood out, but for building a page model this will be enough.
Use the following page model:
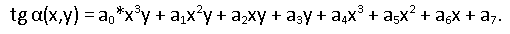
What does this formula tell us? The tangent of the local angle of the rows is a third-degree polynomial horizontally and one degree vertically (here and below we use the usual Cartesian coordinates on the plane). In fact, if we assume that page distortions in space are cylindrical (the sheet bending radius depends only on the x coordinate), then the dependence of the angle of inclination along the vertical when projected onto the image plane will be linear. In the horizontal direction, we believe that a third-degree polynomial will describe the varying angle of inclination with sufficient accuracy. Of course, we tried polynomials of smaller and larger degrees. In general, the choice of model is somewhat arbitrary, it is important that it describes the observed angles well enough. Where do we get them from? Of those very oblique fragments of words. We have a sample of data on the local angles of inclination of the lines for a page; each fragment has its center coordinates and the value of the angle of inclination, which we determine from a set of glued connected components.
We use the usual OLS to find the vector of parameters
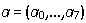. Next, we will filter out the emissions, because we could, by mistake instead of a word fragment, select somewhere else (we had a rough, preliminary analysis).Here
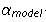- the angle value calculated by the model at a point with the coordinates of the center of the i -th fragment, 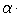- the value of the angle of inclination of the fragment itself (initial data), the values of the angles are given in radians. If, as a result of filtering, we still have a sufficient number of fragments described by the model with a given error, we can refine it by applying the OLS to the remaining data. Thus we get a preliminary model of the page. It describes quite well the curved lines in those parts of the image where we had allocated a sufficient number of word fragments, but in the spine area the solution is inaccurate. If we use it to straighten lines, this area will be distorted.Let's try using our model to “trace” the lines to the end. The centers of the word fragments will serve as priming for the tracking algorithm.
Prepare an image for tracing curved lines:
- binarization
- horizontal closure (row assembly),
- horizontal opening (getting rid of the title, remote elements),
- Gaussian anti-aliasing (slightly blur the lines vertically).
Closing and opening is performed with a window of width R = w / 100 , where w is the width of the image. Smoothing is performed with σ = h / 400 , where h is the height of the image.
We trace the lines, starting from the center of each fragment of the word in both directions.
Each time we shift by a fixed step R horizontally and
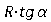vertically. The angle is determined by the model. Make a local maximum search in a vertical column with a height of ± 3 pixels. We continue the process from the revised position. The stopping criterion is the absence of a local maximum or the maximum value does not exceed the noise threshold (T = 30) .As a result of tracking, we get much more data - segments with a refined value of the angle of inclination. We specify our model using this data.
Using the map of angles obtained from the model, we construct a map of local displacements. We take into account the angle of the horizontal perspective at the current point:
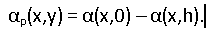
Offset at any point multiplied by
. This allows you to "stretch" the letters in the spine. ► ► ► We receive the image which can already be submitted on input of OCR. To build a pleasing to the eye pictures will have to work. We would like to get something like this:
How to do this (of course, automatically), we offer to reflect on the readers. In conclusion, we note that this algorithm has already found application in the ABBYY FineScanner mobile application, which is now able to process photos of book spreads.
Source: https://habr.com/ru/post/312570/
All Articles