Statistics for mathematics

In modern conditions, interest in data analysis is constantly and intensively growing in completely different areas, such as biology, linguistics, economics, and, of course, IT. The basis of this analysis is statistical methods, and every self-respecting data mining expert needs to understand them.

Unfortunately, really good literature, such that it would be able to provide both mathematically rigorous proofs and clear, intuitive explanations, is not very common. And these lectures , in my opinion, are unusually good for mathematicians who understand probability theory precisely for this reason. Masters are taught in them at the Christian-Albrecht University in Germany on the programs "Mathematics" and "Financial Mathematics". And for those who are interested in how this subject is taught abroad, I have translated these lectures. It took me several months to translate; I diluted the lectures with illustrations, exercises, and footnotes to some theorems. I note that I am not a professional translator, but simply an altruist and amateur in this area, so I will accept any criticism if it is constructive.

In short, the lectures are about:


')

Conditional expectation

This chapter does not relate directly to statistics, however, it is ideal for starting its study. Conditional expectation is the best choice for predicting a random result based on information already available. And this is also a random variable. Here we consider its various properties, such as linearity, monotonicity, monotonic convergence, and others.

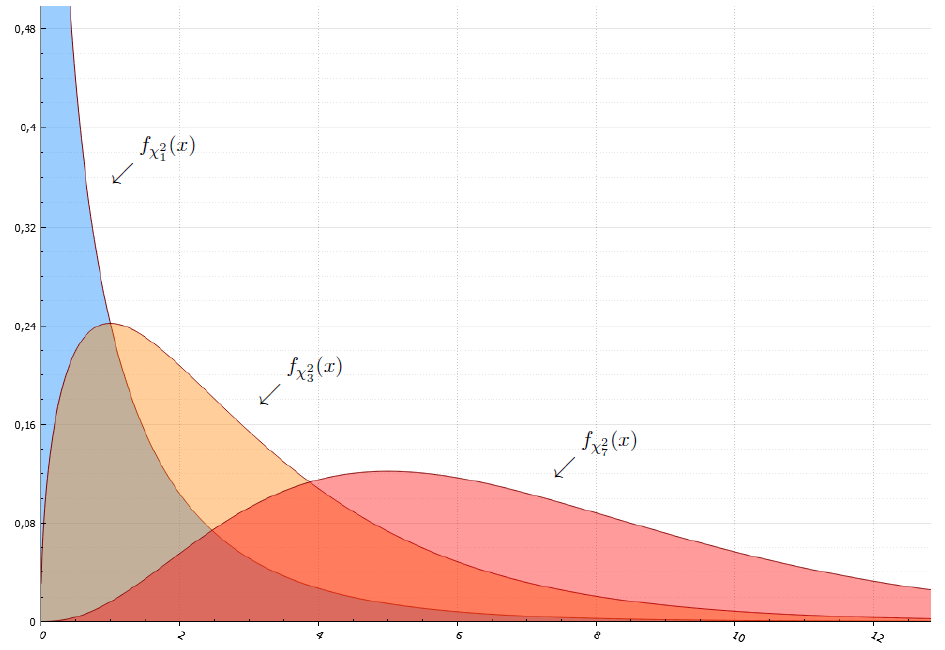
Basics of point estimation

How to estimate the distribution parameter? What is the criterion for this? What methods do you use? This chapter allows you to answer all these questions. Here we introduce the concepts of unbiased estimator and uniformly unbiased estimator with minimal variance. It explains where the chi-square and Student's t-distribution are taken from, and how they are important in estimating the parameters of the normal distribution. It is told that such Rao-Kramer inequality and Fisher information. The concept of an exponential family is also introduced, making it easier to obtain a good estimate many times over.

Bayesian and minimax parameter estimation

It describes a different philosophical approach to evaluation. In this case, the parameter is considered unknown because it is the implementation of a certain random variable with a known (prior) distribution. Observing the result of the experiment, we calculate the so-called posterior distribution of the parameter. Based on this, we can get a Bayesian estimate, where the criterion is minimum loss on average, or a minimax estimate that minimizes the maximum possible losses.

Sufficiency and fullness

This chapter has serious practical significance. Sufficient statistics is a function of the sample, such that it is enough to store only the result of this function in order to evaluate the parameter. There are many such functions, and among them are the so-called minimal sufficient statistics. For example, to estimate the median of the normal distribution, it is enough to store only one number — the arithmetic average over the entire sample. Does this also work for other distributions, for example, for the Cauchy distribution? How do sufficient statistics help in choosing ratings? Here you can find answers to these questions.

Asymptotic properties of estimates

Perhaps the most important and necessary property of an assessment is its viability, that is, striving for a true parameter as the sample size increases. This chapter describes the properties of the estimates known to us, obtained by the statistical methods described in previous chapters. The concepts of asymptotic unbiasedness, asymptotic efficiency, and Kullback-Leibler distance are introduced.

Basics of testing

In addition to the question of how to estimate a parameter unknown to us, we must somehow check whether it satisfies the required properties. For example, an experiment is being conducted in which a new drug is being tested. How to find out if the probability of recovery is higher than with the use of old medicines? This chapter explains how these tests are built. You will learn what is uniformly the most powerful criterion, the Neumann-Pearson criterion, the level of significance, the confidence interval, as well as where do the well-known Gauss criteria and the t-criterion come from.

Asymptotic properties of criteria

Like estimates, the criteria must satisfy certain asymptotic properties. Sometimes situations may arise when the necessary criterion cannot be constructed; however, using the well-known central limit theorem, we construct a criterion that asymptotically tends to the necessary. Here you learn what an asymptotic level of significance is, likelihood ratio method, and how the Bartlett criterion and chi-square independence criterion are constructed.

Linear model

This chapter can be considered as an addition, namely, the use of statistics in the case of linear regression. You will understand what assessments are good and in what conditions. You will learn where the least squares method came from, how to build criteria, and why you need F-distribution.

Links to

• Transfer
• Original
• Source