Neural networks for beginners. Part 1

Hello to all readers of Habrahabr, in this article I want to share with you my experience in the study of neural networks and, as a result, their implementation, using the Java programming language, on the Android platform. My familiarity with neural networks happened when the Prisma application came out. It processes any photo using neural networks and reproduces it from scratch using the chosen style. Having become interested in it, I rushed to look for articles and "tutorials", first of all, on Habré. And to my great surprise, I did not find a single article that clearly and gradually described the algorithm of the operation of neural networks. Information was fragmented and there were no key points. Also, most authors rush to show the code in one or another programming language, without resorting to detailed explanations.

Therefore, now that I have mastered neural networks well enough and found a huge amount of information from various foreign portals, I would like to share this with people in a series of publications where I will gather all the information you need if you are just starting to get acquainted with neural networks. In this article, I will not put a strong emphasis on Java and will explain everything with examples so that you yourself can transfer it to any programming language you need. In subsequent articles, I will talk about my application, written under the android, which predicts the movement of shares or currencies. In other words, everyone who wants to plunge into the world of neural networks and eager for simple and accessible presentation of information or just those who do not understand something and want to pull up, welcome to the cat.

The first and most important discovery of mine was the playlist of the American programmer Jeff Heaton, in which he analyzed in detail and clearly the principles of operation of neural networks and their classification. After viewing this playlist, I decided to create my own neural network, starting with the simplest example. You probably know that when you first start learning a new language, your first program will be Hello World. This is a kind of tradition. In the world of machine learning, there is also a Hello world and this is a neural network solving an exclusive or (XOR) problem. The table is exclusive or looks like this:

a	b	c
0	0	0
0	one	one
one	0	one
one	one	0

Accordingly, the neural network takes as input two numbers and should output another number at the output - the answer. Now about the neural networks themselves.
')

What is a neural network?

A neural network is a sequence of neurons connected by synapses. The structure of the neural network came into the world of programming straight from biology. Thanks to this structure, the machine acquires the ability to analyze and even memorize various information. Neural networks are also able not only to analyze incoming information, but also to reproduce it from its memory. Interested be sure to watch 2 videos from TED Talks: Video 1 , Video 2 ). In other words, the neural network is a machine interpretation of the human brain, in which there are millions of neurons transmitting information in the form of electrical impulses.

What are neural networks?

For now, we will consider examples at the most basic type of neural networks - this is a network of direct distribution (hereinafter referred to as SPR). Also in subsequent articles I will introduce more concepts and tell you about recurrent neural networks. AB, as derived from the name, is a network with a series connection of neural layers, information in it always goes only in one direction.

What are neural networks for?

Neural networks are used to solve complex problems that require analytical calculations similar to those of the human brain. The most common applications of neural networks are:

Classification - the distribution of data by parameters. For example, at the entrance is given a set of people and you need to decide which of them to give a loan and who does not. This work can be done by a neural network, analyzing such information as: age, solvency, credit history, and so on.

Prediction - the ability to predict the next step. For example, rising or falling stocks, based on the situation on the stock market.

Recognition is currently the widest application of neural networks. Used by Google when you are looking for a photo or in the camera phones, when it determines the position of your face and highlights it, and more.

Now, in order to understand how neural networks work, let's take a look at its components and their parameters.

What is a neuron?

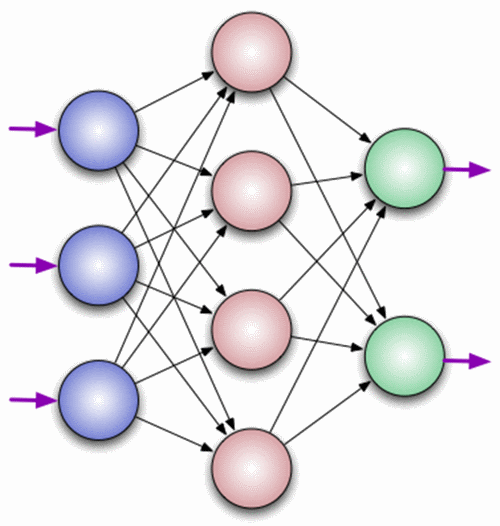
A neuron is a computational unit that receives information, performs simple calculations on it, and passes it on. They are divided into three main types: input (blue), hidden (red) and output (green). There is also a displacement neuron and a context neuron which we will discuss in the next article. In the case when the neural network consists of a large number of neurons, the term layer is introduced. Accordingly, there is an input layer that receives information, n hidden layers (usually no more than 3 of them) that process it and an output layer that displays the result. Each of the neurons has 2 basic parameters: input data (input data) and output data (output data). In the case of an input neuron: input = output. In the others, the input information contains the total information of all neurons from the previous layer, after which, it is normalized using the activation function (for now just present it to f (x)) and enters the output field.


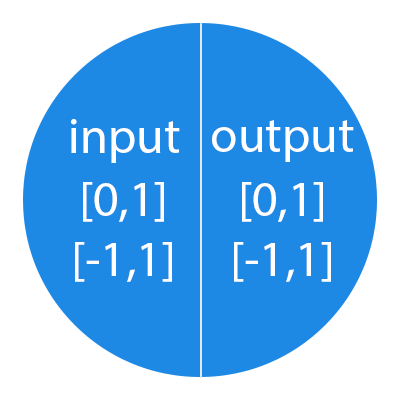
It is important to remember that neurons operate with numbers in the range [0,1] or [-1,1]. And what, you ask, then process the numbers that fall outside this range? At this stage, the easiest answer is to divide 1 by this number. This process is called normalization, and it is very often used in neural networks. More on this later.

What is synapse?

A synapse is the connection between two neurons. Synapses have 1 parameter - weight. Thanks to him, the input information changes when transmitted from one neuron to another. Suppose there are 3 neurons that transmit information to the following. Then we have 3 weights corresponding to each of these neurons. In that neuron, whose weight is greater, that information will be dominant in the next neuron (for example, color mixing). In fact, a set of weights of a neural network or a matrix of weights is a kind of brain of the whole system. Thanks to these weights, input information is processed and turned into a result.

It is important to remember that during the initialization of the neural network, the weights are placed randomly.

How does a neural network work?

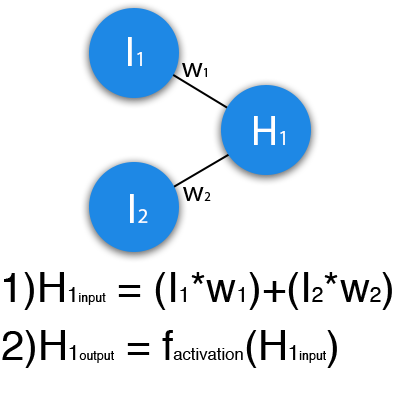
In this example, a part of the neural network is depicted, where the letters I denote the input neurons, the letter H represents the hidden neuron, and the letter w denotes weights. From the formula it is clear that the input information is the sum of all the input data multiplied by the corresponding weight. Then we give input 1 and 0. Let w1 = 0.4 and w2 = 0.7. The input data of the H1 neuron will be as follows: 1 * 0.4 + 0 * 0.7 = 0.4. Now that we have the input data, we can get the output by substituting the input value into the activation function (more on this later). Now that we have the output, we pass it on. And so, we repeat for all layers until we reach the output neuron. By launching such a network for the first time, we will see that the answer is far from correct, because the network is not trained. To improve the results we will train it. But before we learn how to do this, let's introduce a few terms and properties of the neural network.

Activation function

The activation function is a way to normalize the input data (we already talked about this earlier). That is, if you have a large number at the entrance, by passing it through the activation function, you will get an exit in the range you need. There are a lot of activation functions, so we will look at the most basic ones: Linear, Sigmoid (Logistic) and Hyperbolic tangent. Their main differences are the range of values.

Linear function

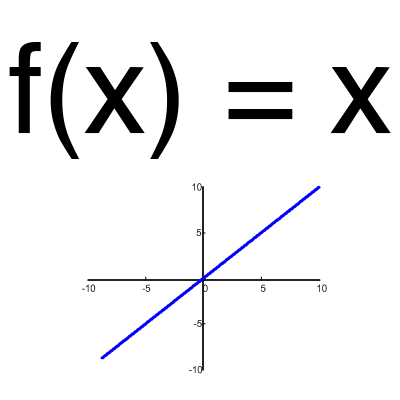
This function is almost never used, except when you need to test a neural network or transmit a value without transformation.

Sigmoid

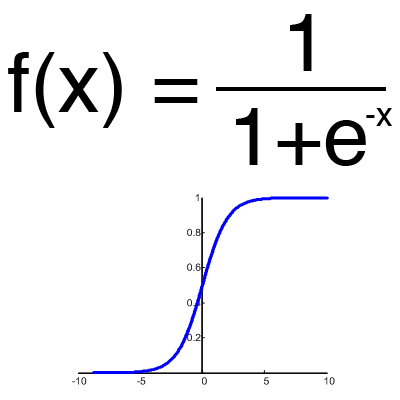
This is the most common activation function, its value range is [0,1]. It shows the majority of examples in the network, it is also sometimes called the logistic function. Accordingly, if in your case there are negative values ​​(for example, stocks can go not only up, but also down), then you need a function that captures negative values.

Hyperbolic tangent

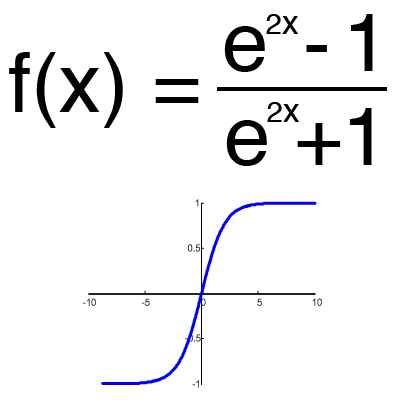
It makes sense to use a hyperbolic tangent, only when your values ​​can be both negative and positive, since the range of the function is [-1,1]. It is impractical to use this function with positive values ​​only as this will significantly worsen the results of your neural network.

Training set

A training set is a sequence of data with which a neural network operates. In our case, the exclusive or (xor) we have only 4 different outcomes, that is, we will have 4 training sets: 0xor0 = 0, 0xor1 = 1, 1xor0 = 1.1xor1 = 0.

Iteration

This is a kind of counter that increases each time a neural network passes one training set. In other words, this is the total number of training sets traversed by the neural network.

The epoch

When the neural network is initialized, this value is set to 0 and has a ceiling that is set manually. The greater the era, the better the network is trained and, accordingly, its result. The era increases each time we go through the entire set of training sets, in our case, 4 sets or 4 iterations.


It is important not to confuse the iteration with the epoch and to understand the sequence of their increment. N first
times the iteration increases, and then the era and not vice versa. In other words, you cannot first train a neural network only on one set, then on another, and so on. You need to train each set once in an era. So, you can avoid computation errors.

Mistake

Error is a percentage value that reflects the discrepancy between the expected and received responses. A mistake is formed every epoch and should go into decline. If this does not happen, then you are doing something wrong. The error can be calculated in different ways, but we will consider only three main methods: Mean Squared Error (hereinafter MSE), Root MSE and Arctan. There is no restriction on use, as in the activation function, and you are free to choose any method that will bring you the best result. One has only to consider that each method counts errors in different ways. In Arctan, the error will almost always be greater, since it works on the principle: the bigger the difference, the bigger the error. Root MSE will have the smallest error, which is why, most often, MSE is used, which maintains a balance in the error calculation.

MSE

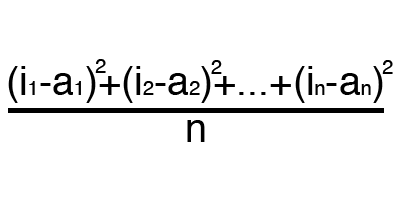
Root MSE

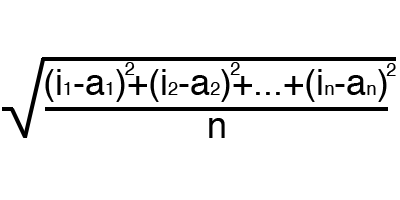
Arctan

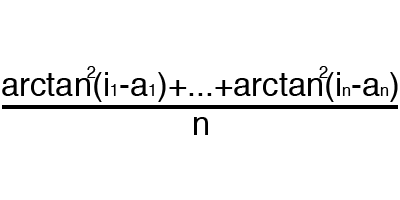
The principle of error counting is the same in all cases. For each set, we consider an error, taking away from the ideal answer, received. Next, either squaring or calculating the square tangent from this difference, after which the resulting number is divided by the number of sets.

Task

Now, to test yourself, calculate the result of a given neural network using sigmoid and its error using MSE.

Data: I1 = 1, I2 = 0, w1 = 0.45, w2 = 0.78, w3 = -0.12, w4 = 0.13, w5 = 1.5, w6 = -2.3.



Thank you very much for your attention! I hope that this article was able to help you in the study of neural networks. In the next article, I will talk about displacement neurons and how to train a neural network using the back propagation method and gradient descent.

Resources used:
- Once
- two
- three