Analysis of the tasks of the first stage of selection to the school programmers HeadHunter 2016
In September 2016, the regular annual selection of young specialists, students and graduates of engineering and mathematical specialties to the HeadHunter School of Programmers was held .
For admission it was proposed to go through several stages, solving logical / mathematical problems.
I will try to analyze the solutions to some typical tasks of the first stage in this article.
PS: For convenience, quick writing and debugging code calculations used JavaScript.
While writing an article, I see, in the sandbox I was already ahead of the topic . However, I have considered other types of tasks, only one has coincided about degrees (but, judging by the comments, no offense to the author is the wrong decision).
Comments and suggestions for alternative solutions are welcome.
')
For admission it was proposed to go through several stages, solving logical / mathematical problems.
I will try to analyze the solutions to some typical tasks of the first stage in this article.
PS: For convenience, quick writing and debugging code calculations used JavaScript.
While writing an article, I see, in the sandbox I was already ahead of the topic . However, I have considered other types of tasks, only one has coincided about degrees (but, judging by the comments, no offense to the author is the wrong decision).
Comments and suggestions for alternative solutions are welcome.
')
Task 1
Consider a spiral in which, starting from 1 in the center, we will successively arrange the numbers clockwise until spiral 5 is 5:
You can check that the sum of all the numbers on the diagonals is 101.
What will be the sum of the numbers on the diagonals, for a spiral size of 1195 by 1195?
Solution 1
We will go from the very center in a spiral and simply sum up the numbers at the corners: 1 + 3 + 5 + 7 + 9 + 13 + 17 + 21 + 25 + ...
You can see that in this sequence, each successive number differs by delta d (initially equal to 2: 3, 5, 7, 9). At the same time, with each transition to the next turn of the helix, the delta between the four angular numbers increases by another 2: 13, 17, 21, 25.
It turns out the sum of the angular numbers of one revolution is calculated by the formula: (v + d) + (v + 2 * d) + (v + 3 * d) + (v + 4 * d) , where v is the last number of the previous round (1 , 9, 25, ...), d - delta. We construct a cycle, increasing the delta d to the size of the helix size .
Alternative solution, as the sum of a quadratic sequence proposed by eandr_67 in the comments:
For a spiral of size = 1195, the sum of the numbers on the diagonals is 1138375521.
Solution 1
We will go from the very center in a spiral and simply sum up the numbers at the corners: 1 + 3 + 5 + 7 + 9 + 13 + 17 + 21 + 25 + ...
You can see that in this sequence, each successive number differs by delta d (initially equal to 2: 3, 5, 7, 9). At the same time, with each transition to the next turn of the helix, the delta between the four angular numbers increases by another 2: 13, 17, 21, 25.
It turns out the sum of the angular numbers of one revolution is calculated by the formula: (v + d) + (v + 2 * d) + (v + 3 * d) + (v + 4 * d) , where v is the last number of the previous round (1 , 9, 25, ...), d - delta. We construct a cycle, increasing the delta d to the size of the helix size .
function task1(size) { for (var v=1, d=2, sum=v; d<size; v+=4*d, d+=2) { sum += 4*v+10*d; } return sum; } Alternative solution, as the sum of a quadratic sequence proposed by eandr_67 in the comments:
function task1_alt(size) { return (size * size * size * 2 / 3.0 + size * size / 2.0 + size * 4 / 3.0 - 1.5); } For a spiral of size = 1195, the sum of the numbers on the diagonals is 1138375521.
Task 2
We define the function P (n, k) as follows: P (n, k) = 1, if n can be represented as a sum of k prime numbers (prime numbers in the record can be repeated, 1 is not a prime number) and P (n, k) = 0 otherwise.
For example, P (10,2) = 1, since 10 can be represented as a sum of 3 + 7 or 5 + 5, and P (11,2) = 0, since no two prime numbers can give a total of 11.
We define the function S (n) as the sum of the values of the function P (i, k) for all i and k such that 1 <= i <= n, 1 <= k <= n.
Thus, S (2) = P (1,1) + P (2,1) + P (1,2) + P (2,2) = 1, S (10) = 20, S (1000) = 248838.
Find the S (17688).
Solution 2
We use the properties of prime numbers:
For k> 3, the values of the function P (i, k) are filled in as consequences of the previous statements. Moreover, all even numbers i> = 4 can be decomposed into a maximum of k = i / 2 primes (k = i / 2-1 for odd numbers).
Let's make a visual matrix, where i are numbers from 1 to n, which can be decomposed into a sum of k prime numbers:
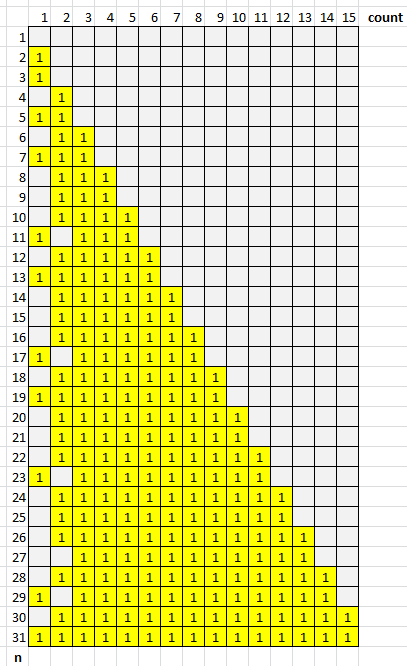
It can be noted that there are such odd numbers that are not simple, and at the same time they cannot be represented as the sum of two prime numbers - in this case, for example, 27 .
We can calculate the number of prime numbers by checking every odd number for a modulus without a residue for all the primes obtained earlier:
The total counting function S (n):
S (17688) = 78193870.
Solution 2
We use the properties of prime numbers:
- Each even number greater than two can be represented as the sum of two primes. ( Goldbach binary problem (or Euler problem) , 2012 checked for all even numbers not exceeding 4 × 10 18 )
- Each odd number greater than 5 can be represented as the sum of three primes. ( Goldbach's ternary problem , proven in 2013)
For k> 3, the values of the function P (i, k) are filled in as consequences of the previous statements. Moreover, all even numbers i> = 4 can be decomposed into a maximum of k = i / 2 primes (k = i / 2-1 for odd numbers).
Let's make a visual matrix, where i are numbers from 1 to n, which can be decomposed into a sum of k prime numbers:
It can be noted that there are such odd numbers that are not simple, and at the same time they cannot be represented as the sum of two prime numbers - in this case, for example, 27 .
We can calculate the number of prime numbers by checking every odd number for a modulus without a residue for all the primes obtained earlier:
// function isPrime(x,primes){ for (var j=0, len=primes.length; j<len; j++){ if (x%primes[j]==0) return false; } return true; } The total counting function S (n):
function task2(n) { for (var i=4, count=2, primes=[2,3]; i<=n; i++){ // - if (i%2==0) { count+=i/2-1; } else { // count+=(i-1)/2-1; // if (i!=(primes[primes.length-1]+2)) { count--; } // - if (isPrime(i,primes)) { count++; // primes[primes.length]=i; } } } return count; } S (17688) = 78193870.
Task 3
The number 125874 and the result of multiplying it by 2 - 251748 can be obtained from each other by rearranging the numbers. Find the smallest positive positive x such that the numbers 2 * x, 3 * x can be obtained from each other by rearranging the digits.
Solution 3
For a simple comparison of numbers by swapping digits, we will bring numbers into strings with characters arranged in ascending order:
And compare these lines with the "ordered" x .
In the comments, Large proposed to exclude from brute force x , in which the first digit is 4 or more: 412, 5230, 60457 ... because multiplying increases the length of the number - and checking such x does not make sense.
We assign such a maximum xFirstMax of the first digit x as the result of the rounded integer division of 9 and the maximum of a and b .
The smallest positive positive x = 142857 (where for a = 2 and b = 3: a * x = 285714 and b * x = 428571).
Solution 3
For a simple comparison of numbers by swapping digits, we will bring numbers into strings with characters arranged in ascending order:
// function sortVal(val) { var str=val.toString(); if (str.length>1){ return str.split("").sort().join(""); } else { return str; } } And compare these lines with the "ordered" x .
In the comments, Large proposed to exclude from brute force x , in which the first digit is 4 or more: 412, 5230, 60457 ... because multiplying increases the length of the number - and checking such x does not make sense.
We assign such a maximum xFirstMax of the first digit x as the result of the rounded integer division of 9 and the maximum of a and b .
function task3(a,b) { // x x var xFirstMax = Math.floor(9/Math.max(a,b)); for (var x=1, xSorted=''; x<=1000000; x++){ // x, if (x.toString()[0]>xFirstMax) continue; // x xSorted=sortVal(x); // x a b if (xSorted==sortVal(a*x) && xSorted==sortVal(b*x)) { var founded=x; break; } } return founded; } The smallest positive positive x = 142857 (where for a = 2 and b = 3: a * x = 285714 and b * x = 428571).
Task 4
If we take 47, turn it upside down and add it, we get 47 + 74 = 121 - a palindrome number.
If you take 349 and do this operation on it three times, you will also get a palindrome:
349 + 943 = 1292
1292 + 2921 = 4213
4213 + 3124 = 7337
Find the number of positive positive integers less than 13110 such that it is impossible to get a palindrome from them in 50 or less applications of the described operation (the operation must be applied at least once).
Solution 4
50 direct summation operations can lead to very large numbers, which, as suggested by Stelet’s comments, will result in unexpected results. Therefore, we will store the numbers as strings. And instead of multiple inversions, we’ll simply sum up the numbers in pairs starting from the ends, which is equivalent to the sum of the number and its inverted copy.
And already to check on the palindrome, it is enough to turn the resulting string and compare the value with itself: 7337 == reverse (7337).
As a result, the number of positive natural numbers is less than maxNum = 13110 such that one cannot get a palindrome from them in 50 operations: 359.
Solution 4
50 direct summation operations can lead to very large numbers, which, as suggested by Stelet’s comments, will result in unexpected results. Therefore, we will store the numbers as strings. And instead of multiple inversions, we’ll simply sum up the numbers in pairs starting from the ends, which is equivalent to the sum of the number and its inverted copy.
And already to check on the palindrome, it is enough to turn the resulting string and compare the value with itself: 7337 == reverse (7337).
function task4(maxNum) { for (var num=1, count=0; num<maxNum; num++){ // 50 for (var op = 1, val=num, palindrome=false; op<=50; op++) { val=val.toString(); // , for (var iMax=val.length-1, i=iMax, j=0, digSum=0, arrSum=[], carry=0; i>=0 && j<=iMax; i--, j++) { // + digSum = parseInt(val[i])+parseInt(val[j])+carry; // 9 if (digSum>9) { // 10 arrSum[arrSum.length]=digSum-10; // carry=1; // if (i==0) arrSum[arrSum.length]=1; } else { arrSum[arrSum.length]=digSum; carry=0; } } val = arrSum.join(""); // if (val == val.split("").reverse().join("")) { // - palindrome = true; break; } } // - if (!palindrome) { count++; } } return count; } As a result, the number of positive natural numbers is less than maxNum = 13110 such that one cannot get a palindrome from them in 50 operations: 359.
Task 5
Consider all possible numbers a b for 1 <a <6 and 1 <b <6:
2 2 = 4, 2 3 = 8, 2 4 = 16 , 2 5 = 32 3 2 = 9, 3 3 = 27, 3 4 = 81, 3 5 = 243, 4 2 = 16 , 4 3 = 64, 4 4 = 256, 4 5 = 1024, 5 2 = 25, 5 3 = 125, 5 4 = 625, 5 5 = 3125
If we remove the repetition, we get 15 different numbers.
How many different numbers a b for 2 <a <149 and 2 <b <121?
Solution 5
In the example above, the variants 2 4 = 16 and 4 2 = 16 coincided, since 4 2 can be represented as (2 * 2) 2 => 2 2 * 2 => 2 4 . Therefore, in order not to raise everything to a power, you can simply reduce a to the power of a prime number, for example: 16 = 2 4 , 27 = 3 3 , 125 = 5 3 , etc.
The number of primes required for the calculations can be determined by the function from Task 2 above, but for simplicity, in this case, we take ready-made values. With that, it is enough to take the first few numbers (2, 3, 5, 7, 11), where the maximum prime number will be no more than the square root of a , since for this case, we will not be able to decompose a <149 into degrees 13: 13 2 > 149.
Looking through a series of prime numbers, we determine whether the number a can be represented by a power. And simply multiply the degree obtained with the corresponding b . From the result, we set the next associative index idx for the array of all variations a b ( arr ), for example:
3 100 => a 3 b 100
and 9 50 => 3 2 * 50 => 3 100 => a 3 b 100
Accordingly, we check the presence of an element with a given index in the arr array.
The final counting function, where a1 , b1 are the corresponding minima of the input values, and a2 , b2 are the maxima of the input values:
For 2 <a <149 and 2 <b <121 different numbers a b : 16529.
Solution 5
In the example above, the variants 2 4 = 16 and 4 2 = 16 coincided, since 4 2 can be represented as (2 * 2) 2 => 2 2 * 2 => 2 4 . Therefore, in order not to raise everything to a power, you can simply reduce a to the power of a prime number, for example: 16 = 2 4 , 27 = 3 3 , 125 = 5 3 , etc.
// function isPowerOf(val,prime){ var power = 0; // if (val%prime == 0) { // while ((val/=prime)>=1) { power++; if (val==1) return power; } } return 0; } The number of primes required for the calculations can be determined by the function from Task 2 above, but for simplicity, in this case, we take ready-made values. With that, it is enough to take the first few numbers (2, 3, 5, 7, 11), where the maximum prime number will be no more than the square root of a , since for this case, we will not be able to decompose a <149 into degrees 13: 13 2 > 149.
Looking through a series of prime numbers, we determine whether the number a can be represented by a power. And simply multiply the degree obtained with the corresponding b . From the result, we set the next associative index idx for the array of all variations a b ( arr ), for example:
3 100 => a 3 b 100
and 9 50 => 3 2 * 50 => 3 100 => a 3 b 100
Accordingly, we check the presence of an element with a given index in the arr array.
The final counting function, where a1 , b1 are the corresponding minima of the input values, and a2 , b2 are the maxima of the input values:
// a1, b1 - , a2, b2 - function task5(a1,a2,b1,b2) { for (var a=a1+1, arr=[], power=1, count=0; a<a2; a++){ // var primes = [2,3,5,7,11]; // , , for (var i=0; i < primes.length; i++) { power = isPowerOf(a,primes[i]); if (power>1) { break; } } for (var b=b1+1, idx=''; b<b2; b++){ // a b idx = (power>1)? "a"+primes[i]+"b"+power*b : "a"+a+"b"+b ; // if (!arr[idx]) { // arr[idx]=1; // count++; } } } return count; } For 2 <a <149 and 2 <b <121 different numbers a b : 16529.
Task 6
In some numbers, you can find sequences of numbers, which together give 10. For example, in the number 3523014, there are four such sequences:
352 3014
3,523,014
3 5230 14
35 23014
You can find such wonderful numbers, each digit of which is included in at least one such sequence.
For example, 3523014 is a remarkable number, and 28546 is not (there is no sequence of numbers in it, giving a total of 10 and including 5).
Find the number of these remarkable numbers in the interval [1, 1900000] (both boundaries - inclusive).
Solution 6
The only solution for this problem that occurred to me was brute force. But I tried to optimize it as much as possible.
Each number num will be divided into an array of digits arrPrep , excluding from it all zeros, since they do not play any role.
To begin with, we can check the sum of all digits of sum at once:
Then we can immediately check the first two and last two digits. If at least one of the pairs in the amount is more than 10, the number is definitely not remarkable, for example: 56 112, 1273 79 .
Now you can proceed to the enumeration of all sequences.
The sums of the sequences will be written to the two-dimensional array s . The main diagonal of which is pre-filled with all the numbers from arrPrep .
If a successful sequence is found, fill in the arrCheck test array with the digits included in this sequence.
At the end, we compare the string representations of the arrPrep array and the arrCheck check array. If equal - all digits of the number are used in at least one successful sequence - i.e. number is wonderful.
The number of remarkable numbers in the interval [1, 1900000]: 152409.
Solution 6
The only solution for this problem that occurred to me was brute force. But I tried to optimize it as much as possible.
Each number num will be divided into an array of digits arrPrep , excluding from it all zeros, since they do not play any role.
To begin with, we can check the sum of all digits of sum at once:
- if it is 10 - i.e. the number is the maximum sequence and can be immediately attributed to the remarkable;
- if less than 10, the number has no sequence and is not remarkable;
Then we can immediately check the first two and last two digits. If at least one of the pairs in the amount is more than 10, the number is definitely not remarkable, for example: 56 112, 1273 79 .
Now you can proceed to the enumeration of all sequences.
The sums of the sequences will be written to the two-dimensional array s . The main diagonal of which is pre-filled with all the numbers from arrPrep .
If a successful sequence is found, fill in the arrCheck test array with the digits included in this sequence.
At the end, we compare the string representations of the arrPrep array and the arrCheck check array. If equal - all digits of the number are used in at least one successful sequence - i.e. number is wonderful.
// "" function isWonderful(num) { var arrRaw=[], arrPrep=[], len=0, sum=0; // arrRaw = num.toString().split(""); for (var i=0, digit=0; i<arrRaw.length; i++){ digit=parseInt(arrRaw[i]); // if (digit>0) { arrPrep[arrPrep.length]=digit; // sum+=digit; } } // len=arrPrep.length; // 10, - "" if (sum==10) { return true; // 10 - "" } else if (sum<10) { return false; } else { // 2 2 10 - "" if ((arrPrep[0]+arrPrep[1])>10 || (arrPrep[len-1]+arrPrep[len-2])>10) { return false; } for (var i=0, s=[]; i<len; i++){ // s[i]=[]; // s[i][i]=arrPrep[i]; } // for (var i=0, arrCheck=[]; i<len-1; i++){ for (var j=i; j<len-1; j++){ // s[i][j+1]=s[i][j]+s[j+1][j+1]; // if (s[i][j+1]==10){ for (var k=i;k<=j+1;k++){ // , arrCheck[k]=s[k][k]; } break; // - } else if (s[i][j+1]>10) { break; } } } // if (arrPrep.join('')==arrCheck.join('')) { // - "" return true; } } return false; } // "" x1, x2 function task6(x1,x2) { for (var x=x1, count=0; x<=x2; x++){ // "" - if (isWonderful(x)) { count++; } } return count; } The number of remarkable numbers in the interval [1, 1900000]: 152409.
Source: https://habr.com/ru/post/312278/
All Articles