GOST R 34.12 '15 on SSE2, or Not So Bad Grasshopper

On Habré, at least twice the new domestic standard block encryption standard GOST R 34.12 2015 Grasshopper was mentioned , ru_crypt in his post reviewed the basic mechanisms and transformations of the new standard, and sebastian_mg dealt with step-by-step tracing of the basic transformation. But many questions remained unanswered. How fast is the new GOST? Can it be optimized, effectively implemented, accelerated by hardware?

About standard GOST R 34.12 '15

Order No. 749 of June 19, 2015 approved GOST R 34.12 2015 as a standard block encryption standard. The standard was developed by the Center for Information Protection and Special Communications of the Federal Security Service of Russia with the participation of InfoTex OJSC, introduced by the Technical Committee on Standardization TC 26 "Cryptographic Information Protection", and entered into force on January 1, 2016.

The official pdf-edition of the standard is downloaded here , and the reference implementation is here (both links lead to the official website of TC 26).

This standard contains descriptions of two block ciphers: “Magma” with a block length of 64 bits and “Grasshopper” with a block length of 128 bits; “Magma” is just a new name for the old, well-known block cipher GOST 28147 '89 (in fact, not quite new, it was under this code name that the old standard block encryption was developed up to 1994) with fixed replacement nodes . “Finally, history has taught us something,” you will say, and you will be right.

In this article we will talk about another cipher having a block length of 128 bits and bearing the code name "Grasshopper". According to the city land, the name of the cipher is not at all connected with the green insect, but is formed by the first syllables of the names of the authors of this cipher: Kuz Ymin, Nech Ayyev, and K.

Description of "Grasshopper"

Differences "Grasshopper" from "Magma"

The new cipher is significantly different from the old one;

doubled block length ( 128 bits, or 16 bytes , versus ~~64 bits, or 8 bytes~~ ),
nontrivial key schedule ( Feistel network as a key schedule against ~~using parts of the secret key as cyclic keys~~ ),
reduced number of cycles ( 10 cycles against ~~32 cycles~~ ),
fundamentally different device of the cipher itself ( LSX cipher against ~~Feistel nets~~ ).

Base transform

The cipher belongs to the LSX cipher class: its basic transformation (block encryption function) is represented by ten cycles of consecutive conversions L (linear transformation), S (substitution) and X (mixing with the cyclic key):

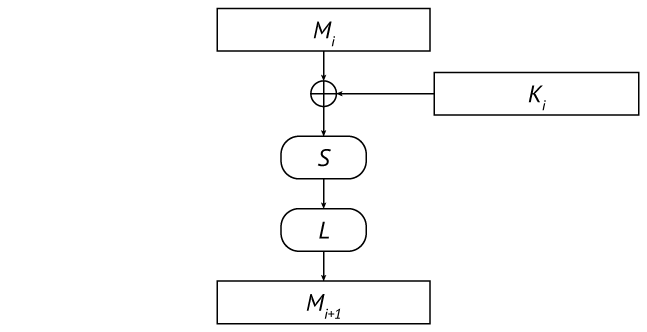
Full cycle of basic conversion

Algebraically, the ciphertext C depends on plaintext P as follows:

$C = X_ {9} \ circ LSX_ {8} \ circ \ dots \ circ LSX_ {0} \ left (P \ right),$

that is, nine complete cycles are followed by the last incomplete (only mixing with the key). Transformation X mixes the intermediate text of the next cycle with the corresponding cyclic key by simple addition modulo 2:

$X (M_i) = M_i \ oplus K_i.$

Transformation S applies the same fixed substitution $\ pi$ to each byte of the intermediate text:

$S (M_i) = \ overline {\ pi (m_0) \ pi (m_1) \ dots \ pi (m_ {15})}, \ text {where} \ pi \ colon \ mathbb {Z} _2 ^ 8 \ mapsto \ mathbb {Z} _2 ^ 8 \ text {and} M_i = \ overline {m_0 m_1 \ dots m_ {15}}.$

The transformation L is a representable linear form over the field GF (256), constructed using an irreducible polynomial

$p (x) = x ^ 8 + x ^ 7 + x ^ 6 + x + 1,$

and boils down to multiplying the vector – line of the intermediate text by some matrix above this field (each byte of text and matrix is a field polynomial represented by its coefficients):

$L (M_i) = M_i \ times M_ {16 \ times 16}.$

Sample code base conversion

/*  S-  . */ static void applySTransformation( uint8_t *block ) { for (int byteIndex = 0; byteIndex < BlockLengthInBytes; byteIndex += 8) { block[byteIndex + 0] = Pi[block[byteIndex + 0]]; block[byteIndex + 1] = Pi[block[byteIndex + 1]]; block[byteIndex + 2] = Pi[block[byteIndex + 2]]; block[byteIndex + 3] = Pi[block[byteIndex + 3]]; block[byteIndex + 4] = Pi[block[byteIndex + 4]]; block[byteIndex + 5] = Pi[block[byteIndex + 5]]; block[byteIndex + 6] = Pi[block[byteIndex + 6]]; block[byteIndex + 7] = Pi[block[byteIndex + 7]]; } } /*  L-  . */ static void applyLTransformation( const uint8_t *input, uint8_t *output ) { for (int byteIndex = 0; byteIndex < BlockLengthInBytes; ++byteIndex) { uint8_t cache = 0; for (int addendIndex = 0; addendIndex < BlockLengthInBytes; ++addendIndex) { cache ^= multiplyInGF256(LTransformationMatrix[addendIndex][byteIndex], input[addendIndex]); } output[byteIndex] = cache; } } /*    . */ static void applyXSLTransformation( const uint8_t *key, uint8_t *block, uint8_t *temporary ) { applyXTransformation(key, block, temporary); applySTransformation(temporary); applyLTransformation(temporary, block); } /*   ( ). */ void encryptBlock( uint8_t *restrict block, const uint8_t *restrict roundKeys ) { uint8_t cache[BlockLengthInBytes] = {0}; int round = 0; for (; round < NumberOfRounds - 1; ++round) { applyXSLTransformation(&roundKeys[BlockLengthInBytes * round], block, cache); } applyXTransformation(&roundKeys[BlockLengthInBytes * round], block, block); }

The calculated transformation matrix L and its inverse in C-friendly form

 /*   L. */ const uint8_t LTransformationMatrix[16][16] = { 0xcf, 0x6e, 0xa2, 0x76, 0x72, 0x6c, 0x48, 0x7a, 0xb8, 0x5d, 0x27, 0xbd, 0x10, 0xdd, 0x84, 0x94, 0x98, 0x20, 0xc8, 0x33, 0xf2, 0x76, 0xd5, 0xe6, 0x49, 0xd4, 0x9f, 0x95, 0xe9, 0x99, 0x2d, 0x20, 0x74, 0xc6, 0x87, 0x10, 0x6b, 0xec, 0x62, 0x4e, 0x87, 0xb8, 0xbe, 0x5e, 0xd0, 0x75, 0x74, 0x85, 0xbf, 0xda, 0x70, 0x0c, 0xca, 0x0c, 0x17, 0x1a, 0x14, 0x2f, 0x68, 0x30, 0xd9, 0xca, 0x96, 0x10, 0x93, 0x90, 0x68, 0x1c, 0x20, 0xc5, 0x06, 0xbb, 0xcb, 0x8d, 0x1a, 0xe9, 0xf3, 0x97, 0x5d, 0xc2, 0x8e, 0x48, 0x43, 0x11, 0xeb, 0xbc, 0x2d, 0x2e, 0x8d, 0x12, 0x7c, 0x60, 0x94, 0x44, 0x77, 0xc0, 0xf2, 0x89, 0x1c, 0xd6, 0x02, 0xaf, 0xc4, 0xf1, 0xab, 0xee, 0xad, 0xbf, 0x3d, 0x5a, 0x6f, 0x01, 0xf3, 0x9c, 0x2b, 0x6a, 0xa4, 0x6e, 0xe7, 0xbe, 0x49, 0xf6, 0xc9, 0x10, 0xaf, 0xe0, 0xde, 0xfb, 0x0a, 0xc1, 0xa1, 0xa6, 0x8d, 0xa3, 0xd5, 0xd4, 0x09, 0x08, 0x84, 0xef, 0x7b, 0x30, 0x54, 0x01, 0xbf, 0x64, 0x63, 0xd7, 0xd4, 0xe1, 0xeb, 0xaf, 0x6c, 0x54, 0x2f, 0x39, 0xff, 0xa6, 0xb4, 0xc0, 0xf6, 0xb8, 0x30, 0xf6, 0xc4, 0x90, 0x99, 0x37, 0x2a, 0x0f, 0xeb, 0xec, 0x64, 0x31, 0x8d, 0xc2, 0xa9, 0x2d, 0x6b, 0x49, 0x01, 0x58, 0x78, 0xb1, 0x01, 0xf3, 0xfe, 0x91, 0x91, 0xd3, 0xd1, 0x10, 0xea, 0x86, 0x9f, 0x07, 0x65, 0x0e, 0x52, 0xd4, 0x60, 0x98, 0xc6, 0x7f, 0x52, 0xdf, 0x44, 0x85, 0x8e, 0x44, 0x30, 0x14, 0xdd, 0x02, 0xf5, 0x2a, 0x8e, 0xc8, 0x48, 0x48, 0xf8, 0x48, 0x3c, 0x20, 0x4d, 0xd0, 0xe3, 0xe8, 0x4c, 0xc3, 0x16, 0x6e, 0x4b, 0x7f, 0xa2, 0x89, 0x0d, 0x64, 0xa5, 0x94, 0x6e, 0xa2, 0x76, 0x72, 0x6c, 0x48, 0x7a, 0xb8, 0x5d, 0x27, 0xbd, 0x10, 0xdd, 0x84, 0x94, 0x01, }; /* ,     L. */ const uint8_t inversedLTransformationMatrix[16][16] = { 0x01, 0x94, 0x84, 0xdd, 0x10, 0xbd, 0x27, 0x5d, 0xb8, 0x7a, 0x48, 0x6c, 0x72, 0x76, 0xa2, 0x6e, 0x94, 0xa5, 0x64, 0x0d, 0x89, 0xa2, 0x7f, 0x4b, 0x6e, 0x16, 0xc3, 0x4c, 0xe8, 0xe3, 0xd0, 0x4d, 0x20, 0x3c, 0x48, 0xf8, 0x48, 0x48, 0xc8, 0x8e, 0x2a, 0xf5, 0x02, 0xdd, 0x14, 0x30, 0x44, 0x8e, 0x85, 0x44, 0xdf, 0x52, 0x7f, 0xc6, 0x98, 0x60, 0xd4, 0x52, 0x0e, 0x65, 0x07, 0x9f, 0x86, 0xea, 0x10, 0xd1, 0xd3, 0x91, 0x91, 0xfe, 0xf3, 0x01, 0xb1, 0x78, 0x58, 0x01, 0x49, 0x6b, 0x2d, 0xa9, 0xc2, 0x8d, 0x31, 0x64, 0xec, 0xeb, 0x0f, 0x2a, 0x37, 0x99, 0x90, 0xc4, 0xf6, 0x30, 0xb8, 0xf6, 0xc0, 0xb4, 0xa6, 0xff, 0x39, 0x2f, 0x54, 0x6c, 0xaf, 0xeb, 0xe1, 0xd4, 0xd7, 0x63, 0x64, 0xbf, 0x01, 0x54, 0x30, 0x7b, 0xef, 0x84, 0x08, 0x09, 0xd4, 0xd5, 0xa3, 0x8d, 0xa6, 0xa1, 0xc1, 0x0a, 0xfb, 0xde, 0xe0, 0xaf, 0x10, 0xc9, 0xf6, 0x49, 0xbe, 0xe7, 0x6e, 0xa4, 0x6a, 0x2b, 0x9c, 0xf3, 0x01, 0x6f, 0x5a, 0x3d, 0xbf, 0xad, 0xee, 0xab, 0xf1, 0xc4, 0xaf, 0x02, 0xd6, 0x1c, 0x89, 0xf2, 0xc0, 0x77, 0x44, 0x94, 0x60, 0x7c, 0x12, 0x8d, 0x2e, 0x2d, 0xbc, 0xeb, 0x11, 0x43, 0x48, 0x8e, 0xc2, 0x5d, 0x97, 0xf3, 0xe9, 0x1a, 0x8d, 0xcb, 0xbb, 0x06, 0xc5, 0x20, 0x1c, 0x68, 0x90, 0x93, 0x10, 0x96, 0xca, 0xd9, 0x30, 0x68, 0x2f, 0x14, 0x1a, 0x17, 0x0c, 0xca, 0x0c, 0x70, 0xda, 0xbf, 0x85, 0x74, 0x75, 0xd0, 0x5e, 0xbe, 0xb8, 0x87, 0x4e, 0x62, 0xec, 0x6b, 0x10, 0x87, 0xc6, 0x74, 0x20, 0x2d, 0x99, 0xe9, 0x95, 0x9f, 0xd4, 0x49, 0xe6, 0xd5, 0x76, 0xf2, 0x33, 0xc8, 0x20, 0x98, 0x94, 0x84, 0xdd, 0x10, 0xbd, 0x27, 0x5d, 0xb8, 0x7a, 0x48, 0x6c, 0x72, 0x76, 0xa2, 0x6e, 0xcf, };

Key Schedule

Indeed, many of the mistakes made when developing the older cipher were corrected, including the vulnerable key schedule. Let me remind the reader that in the code GOST 28147 '89, eight 32-bit parts of the 256-bit secret key were used in right order on encryption cycles from the first to the eighth, from the ninth to the sixteenth, from the seventeenth to the twenty-fourth; and in reverse order on cycles twenty-five to thirty-two:

$K_0, K_1, \ dots, K_6, K_7, \\ K_0, K_1, \ dots, K_6, K_7, \\ K_0, K_1, \ dots, K_6, K_7, \\ K_7, K_6, \ dots, K_1, K_0. \\$

And it is just such a weak key schedule that allowed the attack to be reflected at full GOST, reducing its resistance from 256 bits to 225 bits (for any replacement nodes, from 2 ^ 32 materials on the same key; you can read about this attack here ).

In the new standard, the generation of cyclic keys is carried out according to the Feistel scheme, with the first two cyclic keys being half a 256-bit secret key, and each subsequent pair of cyclic keys is obtained by applying eight cycles of Feistel transformation to the previous pair of cyclic keys, where the cyclic function the LSX transform is used as in the base transform, and a fixed set of constants is used as the cyclic keys in the schema:

$\ left (K_ {2i + 1}, K_ {2i + 2} \ right) = F ^ 8 \ left (K_ {2i - 1}, K_ {2i} \ right); \ text {where} F \ left (x, y \ right) = \ left (LSX_i (y) \ oplus x, y \ right).$

Sample code that implements such a key schedule.

 /*         34.12 '15. */ static void scheduleRoundKeys( uint8_t *restrict roundKeys, const void *restrict key, uint8_t *restrict memory ) { /*     . */ memcpy(&roundKeys[0], key, BlockLengthInBytes * 2); for (int nextKeyIndex = 2, constantIndex = 0; nextKeyIndex != NumberOfRounds; nextKeyIndex += 2) { /*     . */ memcpy(&roundKeys[BlockLengthInBytes * (nextKeyIndex)], &roundKeys[BlockLengthInBytes * (nextKeyIndex - 2)], BlockLengthInBytes * 2); /*   . */ for (int feistelRoundIndex = 0; feistelRoundIndex < NumberOfRoundsInKeySchedule; ++feistelRoundIndex) { applyFTransformation(&roundConstants[BlockLengthInBytes * constantIndex++], &roundKeys[BlockLengthInBytes * (nextKeyIndex)], &roundKeys[BlockLengthInBytes * (nextKeyIndex + 1)], &memory[0], &memory[BlockLengthInBytes]); } } }

Notes
Here, 256 bits of auxiliary memory for cycle conversion are transferred by the memory pointer, but they can be allocated on the stack.
Explicit array indexing with roundKeys cyclic keys roundKeys made for clarity and simplicity, and can be easily replaced with pointer arithmetic.
The applyFTransformation function applies cyclic transformation to semi-blocks of the scheme and produces a swap of these semi-blocks, for example, like this:

 /*       . */ static void applyFTransformation( const uint8_t *restrict key, uint8_t *restrict left, uint8_t *restrict right, uint8_t *restrict temporary1, uint8_t *restrict temporary2 ) { memcpy(temporary1, left, BlockLengthInBytes); applyXSLTransformation(key, temporary1, temporary2); applyXTransformation(temporary1, right, right); swapBlocks(left, right, temporary2); }

Computed cyclic keys in a key schedule in a C-friendly format

 const uint8_t roundConstants[512] = { 0x6e, 0xa2, 0x76, 0x72, 0x6c, 0x48, 0x7a, 0xb8, 0x5d, 0x27, 0xbd, 0x10, 0xdd, 0x84, 0x94, 0x01, 0xdc, 0x87, 0xec, 0xe4, 0xd8, 0x90, 0xf4, 0xb3, 0xba, 0x4e, 0xb9, 0x20, 0x79, 0xcb, 0xeb, 0x02, 0xb2, 0x25, 0x9a, 0x96, 0xb4, 0xd8, 0x8e, 0x0b, 0xe7, 0x69, 0x04, 0x30, 0xa4, 0x4f, 0x7f, 0x03, 0x7b, 0xcd, 0x1b, 0x0b, 0x73, 0xe3, 0x2b, 0xa5, 0xb7, 0x9c, 0xb1, 0x40, 0xf2, 0x55, 0x15, 0x04, 0x15, 0x6f, 0x6d, 0x79, 0x1f, 0xab, 0x51, 0x1d, 0xea, 0xbb, 0x0c, 0x50, 0x2f, 0xd1, 0x81, 0x05, 0xa7, 0x4a, 0xf7, 0xef, 0xab, 0x73, 0xdf, 0x16, 0x0d, 0xd2, 0x08, 0x60, 0x8b, 0x9e, 0xfe, 0x06, 0xc9, 0xe8, 0x81, 0x9d, 0xc7, 0x3b, 0xa5, 0xae, 0x50, 0xf5, 0xb5, 0x70, 0x56, 0x1a, 0x6a, 0x07, 0xf6, 0x59, 0x36, 0x16, 0xe6, 0x05, 0x56, 0x89, 0xad, 0xfb, 0xa1, 0x80, 0x27, 0xaa, 0x2a, 0x08, 0x98, 0xfb, 0x40, 0x64, 0x8a, 0x4d, 0x2c, 0x31, 0xf0, 0xdc, 0x1c, 0x90, 0xfa, 0x2e, 0xbe, 0x09, 0x2a, 0xde, 0xda, 0xf2, 0x3e, 0x95, 0xa2, 0x3a, 0x17, 0xb5, 0x18, 0xa0, 0x5e, 0x61, 0xc1, 0x0a, 0x44, 0x7c, 0xac, 0x80, 0x52, 0xdd, 0xd8, 0x82, 0x4a, 0x92, 0xa5, 0xb0, 0x83, 0xe5, 0x55, 0x0b, 0x8d, 0x94, 0x2d, 0x1d, 0x95, 0xe6, 0x7d, 0x2c, 0x1a, 0x67, 0x10, 0xc0, 0xd5, 0xff, 0x3f, 0x0c, 0xe3, 0x36, 0x5b, 0x6f, 0xf9, 0xae, 0x07, 0x94, 0x47, 0x40, 0xad, 0xd0, 0x08, 0x7b, 0xab, 0x0d, 0x51, 0x13, 0xc1, 0xf9, 0x4d, 0x76, 0x89, 0x9f, 0xa0, 0x29, 0xa9, 0xe0, 0xac, 0x34, 0xd4, 0x0e, 0x3f, 0xb1, 0xb7, 0x8b, 0x21, 0x3e, 0xf3, 0x27, 0xfd, 0x0e, 0x14, 0xf0, 0x71, 0xb0, 0x40, 0x0f, 0x2f, 0xb2, 0x6c, 0x2c, 0x0f, 0x0a, 0xac, 0xd1, 0x99, 0x35, 0x81, 0xc3, 0x4e, 0x97, 0x54, 0x10, 0x41, 0x10, 0x1a, 0x5e, 0x63, 0x42, 0xd6, 0x69, 0xc4, 0x12, 0x3c, 0xd3, 0x93, 0x13, 0xc0, 0x11, 0xf3, 0x35, 0x80, 0xc8, 0xd7, 0x9a, 0x58, 0x62, 0x23, 0x7b, 0x38, 0xe3, 0x37, 0x5c, 0xbf, 0x12, 0x9d, 0x97, 0xf6, 0xba, 0xbb, 0xd2, 0x22, 0xda, 0x7e, 0x5c, 0x85, 0xf3, 0xea, 0xd8, 0x2b, 0x13, 0x54, 0x7f, 0x77, 0x27, 0x7c, 0xe9, 0x87, 0x74, 0x2e, 0xa9, 0x30, 0x83, 0xbc, 0xc2, 0x41, 0x14, 0x3a, 0xdd, 0x01, 0x55, 0x10, 0xa1, 0xfd, 0xcc, 0x73, 0x8e, 0x8d, 0x93, 0x61, 0x46, 0xd5, 0x15, 0x88, 0xf8, 0x9b, 0xc3, 0xa4, 0x79, 0x73, 0xc7, 0x94, 0xe7, 0x89, 0xa3, 0xc5, 0x09, 0xaa, 0x16, 0xe6, 0x5a, 0xed, 0xb1, 0xc8, 0x31, 0x09, 0x7f, 0xc9, 0xc0, 0x34, 0xb3, 0x18, 0x8d, 0x3e, 0x17, 0xd9, 0xeb, 0x5a, 0x3a, 0xe9, 0x0f, 0xfa, 0x58, 0x34, 0xce, 0x20, 0x43, 0x69, 0x3d, 0x7e, 0x18, 0xb7, 0x49, 0x2c, 0x48, 0x85, 0x47, 0x80, 0xe0, 0x69, 0xe9, 0x9d, 0x53, 0xb4, 0xb9, 0xea, 0x19, 0x05, 0x6c, 0xb6, 0xde, 0x31, 0x9f, 0x0e, 0xeb, 0x8e, 0x80, 0x99, 0x63, 0x10, 0xf6, 0x95, 0x1a, 0x6b, 0xce, 0xc0, 0xac, 0x5d, 0xd7, 0x74, 0x53, 0xd3, 0xa7, 0x24, 0x73, 0xcd, 0x72, 0x01, 0x1b, 0xa2, 0x26, 0x41, 0x31, 0x9a, 0xec, 0xd1, 0xfd, 0x83, 0x52, 0x91, 0x03, 0x9b, 0x68, 0x6b, 0x1c, 0xcc, 0x84, 0x37, 0x43, 0xf6, 0xa4, 0xab, 0x45, 0xde, 0x75, 0x2c, 0x13, 0x46, 0xec, 0xff, 0x1d, 0x7e, 0xa1, 0xad, 0xd5, 0x42, 0x7c, 0x25, 0x4e, 0x39, 0x1c, 0x28, 0x23, 0xe2, 0xa3, 0x80, 0x1e, 0x10, 0x03, 0xdb, 0xa7, 0x2e, 0x34, 0x5f, 0xf6, 0x64, 0x3b, 0x95, 0x33, 0x3f, 0x27, 0x14, 0x1f, 0x5e, 0xa7, 0xd8, 0x58, 0x1e, 0x14, 0x9b, 0x61, 0xf1, 0x6a, 0xc1, 0x45, 0x9c, 0xed, 0xa8, 0x20, };

Replacement Unit Device

In the standard, the replacement node is specified in a table of values; cipher developers claim that this table was obtained by iterating random tables of values with regard to the requirements for linear and differential properties.

Substitution layer, S-transform

Replacement node and reverse to it in C-friendly form

 /*   pi    34.12  2015. */ const uint8_t Pi[256] = { 0xfc, 0xee, 0xdd, 0x11, 0xcf, 0x6e, 0x31, 0x16, 0xfb, 0xc4, 0xfa, 0xda, 0x23, 0xc5, 0x04, 0x4d, 0xe9, 0x77, 0xf0, 0xdb, 0x93, 0x2e, 0x99, 0xba, 0x17, 0x36, 0xf1, 0xbb, 0x14, 0xcd, 0x5f, 0xc1, 0xf9, 0x18, 0x65, 0x5a, 0xe2, 0x5c, 0xef, 0x21, 0x81, 0x1c, 0x3c, 0x42, 0x8b, 0x01, 0x8e, 0x4f, 0x05, 0x84, 0x02, 0xae, 0xe3, 0x6a, 0x8f, 0xa0, 0x06, 0x0b, 0xed, 0x98, 0x7f, 0xd4, 0xd3, 0x1f, 0xeb, 0x34, 0x2c, 0x51, 0xea, 0xc8, 0x48, 0xab, 0xf2, 0x2a, 0x68, 0xa2, 0xfd, 0x3a, 0xce, 0xcc, 0xb5, 0x70, 0x0e, 0x56, 0x08, 0x0c, 0x76, 0x12, 0xbf, 0x72, 0x13, 0x47, 0x9c, 0xb7, 0x5d, 0x87, 0x15, 0xa1, 0x96, 0x29, 0x10, 0x7b, 0x9a, 0xc7, 0xf3, 0x91, 0x78, 0x6f, 0x9d, 0x9e, 0xb2, 0xb1, 0x32, 0x75, 0x19, 0x3d, 0xff, 0x35, 0x8a, 0x7e, 0x6d, 0x54, 0xc6, 0x80, 0xc3, 0xbd, 0x0d, 0x57, 0xdf, 0xf5, 0x24, 0xa9, 0x3e, 0xa8, 0x43, 0xc9, 0xd7, 0x79, 0xd6, 0xf6, 0x7c, 0x22, 0xb9, 0x03, 0xe0, 0x0f, 0xec, 0xde, 0x7a, 0x94, 0xb0, 0xbc, 0xdc, 0xe8, 0x28, 0x50, 0x4e, 0x33, 0x0a, 0x4a, 0xa7, 0x97, 0x60, 0x73, 0x1e, 0x00, 0x62, 0x44, 0x1a, 0xb8, 0x38, 0x82, 0x64, 0x9f, 0x26, 0x41, 0xad, 0x45, 0x46, 0x92, 0x27, 0x5e, 0x55, 0x2f, 0x8c, 0xa3, 0xa5, 0x7d, 0x69, 0xd5, 0x95, 0x3b, 0x07, 0x58, 0xb3, 0x40, 0x86, 0xac, 0x1d, 0xf7, 0x30, 0x37, 0x6b, 0xe4, 0x88, 0xd9, 0xe7, 0x89, 0xe1, 0x1b, 0x83, 0x49, 0x4c, 0x3f, 0xf8, 0xfe, 0x8d, 0x53, 0xaa, 0x90, 0xca, 0xd8, 0x85, 0x61, 0x20, 0x71, 0x67, 0xa4, 0x2d, 0x2b, 0x09, 0x5b, 0xcb, 0x9b, 0x25, 0xd0, 0xbe, 0xe5, 0x6c, 0x52, 0x59, 0xa6, 0x74, 0xd2, 0xe6, 0xf4, 0xb4, 0xc0, 0xd1, 0x66, 0xaf, 0xc2, 0x39, 0x4b, 0x63, 0xb6, }; /*  ,   pi,    34.12  2015. */ const uint8_t InversedPi[256] = { 0xa5, 0x2d, 0x32, 0x8f, 0x0e, 0x30, 0x38, 0xc0, 0x54, 0xe6, 0x9e, 0x39, 0x55, 0x7e, 0x52, 0x91, 0x64, 0x03, 0x57, 0x5a, 0x1c, 0x60, 0x07, 0x18, 0x21, 0x72, 0xa8, 0xd1, 0x29, 0xc6, 0xa4, 0x3f, 0xe0, 0x27, 0x8d, 0x0c, 0x82, 0xea, 0xae, 0xb4, 0x9a, 0x63, 0x49, 0xe5, 0x42, 0xe4, 0x15, 0xb7, 0xc8, 0x06, 0x70, 0x9d, 0x41, 0x75, 0x19, 0xc9, 0xaa, 0xfc, 0x4d, 0xbf, 0x2a, 0x73, 0x84, 0xd5, 0xc3, 0xaf, 0x2b, 0x86, 0xa7, 0xb1, 0xb2, 0x5b, 0x46, 0xd3, 0x9f, 0xfd, 0xd4, 0x0f, 0x9c, 0x2f, 0x9b, 0x43, 0xef, 0xd9, 0x79, 0xb6, 0x53, 0x7f, 0xc1, 0xf0, 0x23, 0xe7, 0x25, 0x5e, 0xb5, 0x1e, 0xa2, 0xdf, 0xa6, 0xfe, 0xac, 0x22, 0xf9, 0xe2, 0x4a, 0xbc, 0x35, 0xca, 0xee, 0x78, 0x05, 0x6b, 0x51, 0xe1, 0x59, 0xa3, 0xf2, 0x71, 0x56, 0x11, 0x6a, 0x89, 0x94, 0x65, 0x8c, 0xbb, 0x77, 0x3c, 0x7b, 0x28, 0xab, 0xd2, 0x31, 0xde, 0xc4, 0x5f, 0xcc, 0xcf, 0x76, 0x2c, 0xb8, 0xd8, 0x2e, 0x36, 0xdb, 0x69, 0xb3, 0x14, 0x95, 0xbe, 0x62, 0xa1, 0x3b, 0x16, 0x66, 0xe9, 0x5c, 0x6c, 0x6d, 0xad, 0x37, 0x61, 0x4b, 0xb9, 0xe3, 0xba, 0xf1, 0xa0, 0x85, 0x83, 0xda, 0x47, 0xc5, 0xb0, 0x33, 0xfa, 0x96, 0x6f, 0x6e, 0xc2, 0xf6, 0x50, 0xff, 0x5d, 0xa9, 0x8e, 0x17, 0x1b, 0x97, 0x7d, 0xec, 0x58, 0xf7, 0x1f, 0xfb, 0x7c, 0x09, 0x0d, 0x7a, 0x67, 0x45, 0x87, 0xdc, 0xe8, 0x4f, 0x1d, 0x4e, 0x04, 0xeb, 0xf8, 0xf3, 0x3e, 0x3d, 0xbd, 0x8a, 0x88, 0xdd, 0xcd, 0x0b, 0x13, 0x98, 0x02, 0x93, 0x80, 0x90, 0xd0, 0x24, 0x34, 0xcb, 0xed, 0xf4, 0xce, 0x99, 0x10, 0x44, 0x40, 0x92, 0x3a, 0x01, 0x26, 0x12, 0x1a, 0x48, 0x68, 0xf5, 0x81, 0x8b, 0xc7, 0xd6, 0x20, 0x0a, 0x08, 0x00, 0x4c, 0xd7, 0x74, };

However, all secrets sooner or later becomes clear, and the method of selecting a replacement node is no exception. A team of cryptographers from Luxembourg, headed by Alex Biryukov, was able to detect certain kinds of patterns in the statistical characteristics of the replacement node, which, in turn, allowed them to recover the method of obtaining it. You can read more about this method in their article published on iacr.org.

Secret structure replacement node

Algorithmic optimization

A team of researchers from OAO InfoTeKS, specifically Mikhail Borodin and Andrey Rybkin, managed to borrow algorithmic optimization of vector multiplication by a column from the high-speed implementations of the AES (Rijndael) cipher, which allows replacing the classical multiplication implementation with O (n ^ 2) multiplications in the field by O (n) additions modulo two vectors of length O (n) using pre-calculated tables, and which was reported at the RusCrypto conference, in memory of me, in 2014.

In short, the optimization is as follows: for example, as a result of the product of some vector U

$U = \ left (u_0, u_1, \ dots, u_ {n - 1} \ right) \ in \ left (\ mathrm {GF} (256) \ right) ^ n$

to matrix A

$A = \ begin {pmatrix} a_ {0, 0} & amp; a_ {0, 1} & amp; \ cdots & amp; a_ {0, n-1} \\ a_ {1, 0} & amp; a_ {1, 1} & amp; \ cdots & amp; a_ {1, n-1} \\ \ vdots & amp; \ vdots & amp; \ ddots & amp; \ vdots \\ a_ {n-1, 0} & amp; a_ {n-1, 1} & amp; \ cdots & amp; a_ {n-1, n-1} \ end {pmatrix} _ {n \ times n} \ in \ left (GF (256) \ right) ^ {n \ times n}$

turned out vector V :

$V = U \ times A = \ left (v_0, v_1, \ dots, v_ {n-1} \ right).$

The traditional way to calculate the components of this vector is to sequentially scalar multiply the rows of the vector U by the columns of the matrix A :

$v_i = \ bigoplus_ {j = 0} ^ {n-1} u_j a_ {j, i}$

The calculation of each of the n components of the vector V implies n multiplication operations in the field and the n-1 modulo-2 addition operation, so the complexity of calculating all the components is O (n ^ 2). Yes, of course, you can not multiply in the field each time; you can calculate the logarithm tables and exponents in advance; you can even calculate in advance the works of all possible bytes on the matrix elements (the matrix is fixed and does not change during the encryption process), and store ~ 256 tables of 256 byte-products. Are there identical elements in the matrix? Well, the number of tables can be reduced, but the asymptotic complexity will not change.

And you can go the other way. Instead of calculating each component of a work vector as the sum of n single-byte projections, we use the feature of multiplying the vector by the matrix and calculate all the components of the vector at once as the sum of n vectors:

$V = \ left (\ bigoplus_j m_j a_ {j, 0}, \ bigoplus_j m_j a_ {j, 1}, \ dots, \ bigoplus_j m_j a_ {j, n-1} \ right) = \ bigoplus_j m_j \ left (a_ {j, 0}, a_ {j, 1}, \ dots, a_ {j, n-1} \ right).$

It would seem that changed? The same operations, but in a different order. I note, however, that, firstly, the sum of the terms increased from one byte to n bytes, and such amounts can (and should) be calculated in long registers, and, secondly, each term is an component-wise product of one (!) Byte of the vector on a fixed row matrix.

Here in more detail: you can calculate in advance the work of the form

$m_i \ times \ left (a_ {i, 0}, a_ {i, 1}, \ dots, a_ {i, n-1} \ right) \ quad \ forall m_i \ in \ mathrm {GF} (256),$

that is, multiply the known row i of the matrix A by all possible values of byte i of the vector U , and instead of multiplying the next byte by this row, simply read the product from the table. Then the multiplication of the vector by the matrix is reduced to reading the n product lines from the previously calculated table and the bitwise addition of these lines to get the resultant vector V. So, quite simply, you can greatly simplify the multiplication of a vector by a matrix to O (n), if the addition of vectors is considered elementary operations.

In the case of GOST R 34.12 '15 n = 16, for example, vectors have lengths of 16 bytes, or 128 bits, and fit very well into long XMM registers, and for their addition additional processor instructions are provided, for example, pxor .

Everything is very cool, but what about the replacement node? The reader will certainly notice that in the presence of byte replacement nodes, which generally do not vectorize, all the algorithmic charms of such an L -transformation are leveled by the cost of loading vectors into registers before conversion and unloading after conversion. Good question.

Good, and very elegantly solved. It turns out that the replacement nodes can simply be “glued together” with the L -transform, replacing the pre-calculated lines of the product with

$m_i \ times \ left (a_ {i, 0}, a_ {i, 1}, \ dots, a_ {i, n-1} \ right) \ quad \ forall m_i \ in \ mathrm {GF} (256),$

$\ pi (m_i) \ times \ left (a_ {i, 0}, a_ {i, 1}, \ dots, a_ {i, n-1} \ right) \ quad \ forall m_i \ in \ mathrm {GF} (256),$

Then one full encryption cycle comes down to

blending with the key ( pxor ),
using the glued LS transform (in the best case, these are 16 downloads of 128-bit vectors from the cache and 15 additions pxor ).

Of course, such optimizations are not free, to use them you will need, first, to compute and store in the cache one of the two tables with strings-works, each of which contains 256 * 16 * 16 bytes, or 64 KB. Why are there two tables? Because the inverse transformation used in decryption will require multiplication by the inverse of the L matrix, and will entail new works.

Secondly, gluing replacement nodes with multiplication by a matrix is possible only if a block is first applied to the block, and then multiplied, so the decryption algorithm will have to be slightly modified. The clear text is obtained from the ciphertext by simply reversing the whole scheme (all transformations are reversible):

$P = X_0 S ^ {- 1} L ^ {- 1} \ circ \ dots \ circ X_8 S ^ {- 1} L ^ {- 1} \ circ X_9 (C).$

Note that when deciphering "in the forehead" to the intermediate text, they first apply multiplication by the inverse matrix, and then the action by substitution, therefore, in order to glue these transformations even here, we will have to reorder the decryption algorithm.

I note that the composition of the transformations

$V = L ^ {- 1} X_ {K_i} S ^ {- 1} (U) = L ^ {- 1} \ left (S ^ {- 1} (U) \ oplus K_i \ right)$

identical composition

$V = L ^ {- 1} S ^ {- 1} (U) \ oplus L ^ {- 1} \ left (K_i \ right) = X_ {L ^ {- 1} (K_i)} L ^ {- 1 } S ^ {- 1} (U)$

due to the linearity of the transform l . Then decryption can be done as follows:

$P = X_ {K_0} S ^ {- 1} \ circ \ left (X_ {L ^ {- 1} (K_1)} L ^ {- 1} S ^ {- 1} \ right) \ circ \ dots \ circ \ left (X_ {L ^ {- 1} (K_8)} L ^ {- 1} S ^ {- 1} \ right) \ circ X_ {L ^ {- 1} (K_9)} L ^ {- 1} S ^ {- 1} S (C)$

Here, each of the transformations inverse to SL can be carried out according to a scheme similar to that considered. I will not post computed tables of product lines — they are too large even for spoilers; they can be found, for example, here .

Optimization using SSE2

In principle, everything is clear with the basic transformations, it remains to put all these optimizations on asm.
To work with blocks, I suggest using the SSE2 instruction set, we will use the movdqu and movdqa to load and unload data into registers, the pxor , pand , pandn for boolean operations, the psrlw and psllw for bitwise shifts, pextrw for unloading register bytes.

Yes, there is another subtlety of the implementation of GOST R 34.12 '15. In addition to general algorithmic optimizations like those described above, to further accelerate performance, you need to take into account the features of the assembler and the features of the scheduler, which instructions can be put on parallel execution on different executing devices.

Consideration of the features of address arithmetic

The first feature of the implementation of the algorithm is related to the fact that, if you do not take into account the device of the pre-calculated table and indirect index addressing with offset, then when compiling you can get something like the following exhaust of addition with the next line-product:

 pextrb xmmX, eax, i ;   i (SSE 4.1)  32--  eax movzxd rcx, eax ;     64--  rcx add rcx, rcx ;    pxor xmmY, [rbx + 8*rcx + 0xi000] ;

In registers at the same time are stored:

rbx contains the base offset address of the table,
xmmX contains an input block,
xmmY contains the output block (battery, amount),
eax and rcx are used to highlight and double byte offset.

It should be borne in mind that the precomputed table is arranged as follows:

 uint8_t table[16][256][16],

that is, the values of the product lines are stored in this table continuously, one after another, the external index i corresponds to the i- th row of the L -transformation matrix, the average index j is equal to the i- th byte of the input block, and the internal index k corresponds to the byte index of the next addend:

 Xi = table[i][input[i]][0] ... [16]

Thus, the address of the first byte of the next addend Xi is expressed as follows:

 [Xi] = rbx + (0x1000 * i) + (16 * input[i]),

Where

(0x1000 * i) corresponds to the offset of the current row ( table[i] ),
(16 * input[i]) corresponds to the offset of the current addend Xi ( table[i][input[i]] ).

So, the value of the current byte has to be multiplied by 16, but address arithmetic allows you to use the maximum value of the coefficient factor equal to eight. Therefore, the compiler has to shift the value of the byte in rcx , double it, and only then calculate the address Xi .

In order to avoid such excesses, you can use the ideology of SIMD, and calculate the given displacements in advance, and not by means of address arithmetic.

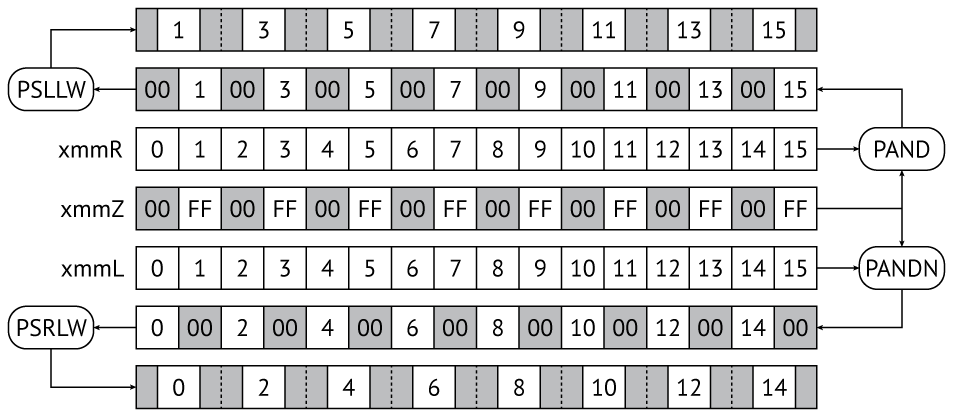
( Xi )

0..15 , 00 FF .

00FF 00FF 00FF 00FF 00FF 00FF 00FF 00FF pand pandn ; c psrlw psllw ( 16) , .
, L - :

 pand xmmR, xmmZ ;    pandn xmmL, xmmZ ;    psllw xmmR, 4 ;    psrlw xmmL, 4 ;

xmmZ . Xi :

 pextrw eax, i ;    i pxor xmmY, [rbx + rax + 0xi000] ;

Intel AMD , , , , , .

, , , . LS - 128- Xi , , , ( ) : .

, ( )

 .code extern bitmask:xmmword extern precomputedLSTable:xmmword encrypt_block proc initialising: movdqu xmm0, [rcx] ; [unaligned] loading block lea r8, [precomputedLSTable + 01000h] ; [aligned] aliasing table base with offset lea r11, [precomputedLSTable] ; [aligned] aliasing table base movdqa xmm4, [bitmask] ; [aligned] loading bitmask mov r10d, 9 ; number of rounds, base 0 round: pxor xmm0, [rdx] ; [aligned] mixing with round key movaps xmm1, xmm4 ; securing bitmask from @xmm4 movaps xmm2, xmm4 ; securing bitmask from @xmm4 pand xmm2, xmm0 ; calculating offsets pandn xmm1, xmm0 psrlw xmm2, 4 psllw xmm1, 4 pextrw eax, xmm1, 0h ; accumulating caches movdqa xmm0, [r11 + rax + 00000h] pextrw eax, xmm2, 0h movdqa xmm3, [r8 + rax + 00000h] pextrw eax, xmm1, 1h pxor xmm0, [r11 + rax + 02000h] pextrw eax, xmm2, 1h pxor xmm3, [r8 + rax + 02000h] pextrw eax, xmm1, 2h pxor xmm0, [r11 + rax + 04000h] pextrw eax, xmm2, 2h pxor xmm3, [r8 + rax + 04000h] pextrw eax, xmm1, 3h pxor xmm0, [r11 + rax + 06000h] pextrw eax, xmm2, 3h pxor xmm3, [r8 + rax + 06000h] pextrw eax, xmm1, 4h pxor xmm0, [r11 + rax + 08000h] pextrw eax, xmm2, 4h pxor xmm3, [r8 + rax + 08000h] pextrw eax, xmm1, 5h pxor xmm0, [r11 + rax + 0a000h] pextrw eax, xmm2, 5h pxor xmm3, [r8 + rax + 0a000h] pextrw eax, xmm1, 6h pxor xmm0, [r11 + rax + 0c000h] pextrw eax, xmm2, 6h pxor xmm3, [r8 + rax + 0c000h] pextrw eax, xmm1, 7h pxor xmm0, [r11 + rax + 0e000h] pextrw eax, xmm2, 7h pxor xmm3, [r8 + rax + 0e000h] pxor xmm0, xmm3 ; mixing caches add rdx, 10h ; advancing to next round key dec r10 ; decrementing round index jnz round last_round: pxor xmm0, [rdx] ; [aligned] mixing with round key movdqu [rcx], xmm0 ; [unaligned] storing block ret encrypt_block endp end

Conclusion

; , Intel Core i7-2677M Sandy Bridge @ 1.80 GHz, 120 / SSE 1.3 / .

— , :

( , );
, , .

34.12 '15 , . C99, , . CMake 3.2.1+ , C99. , ( compact ), , SIMD ( optimised ) SSE2 ( SIMD ).

Travis CI , ( , ) CTest std::chrono C++11.

Source: https://habr.com/ru/post/312224/

All Articles