Quantum hashing. Lecture in Yandex
Farid Mansurovich Ablaev - Head of the Department of Theoretical Cybernetics, Kazan Federal University. Arriving at the Moscow office of Yandex, Farid Mansurovich spoke about algorithms that are potentially suitable for running on quantum computers. Such devices are still very few, and they are not really mastered by even the most advanced companies. But when they begin to become cheaper, the specialists will already have some groundwork to begin their use.
One of the areas where significant changes can occur with the advent of quantum systems is digital signature mechanisms. The report reveals a hashing algorithm that radically exceeds analogs for classic computers. Under the cut - a detailed transcript and slides.
Most of the slides will be in English, but I think my colleagues will excuse me. It is not always possible to translate everything, well, there is not always a need.
')

This report is based on the works that are presented here. With our first work - I myself am a mathematician - we were invited to the journal Laser Physics Letters, which, unlike the high-ranking mathematical journals, with the corresponding index slightly less than 1, has an index of 3.2. Now, when all Hirsch Indices and others are taken into account, it turns out to be useful to publish in such journals - physical ones.
One of the latest results was published at the seminar Algebra in Computational Complexity, there is such a German center. These results can be seen there. Archive is understandable.

I'll start with motivation. Daniel joked that soon there will be a quantum computer, and we will all use it. In Kazan, there is a group that assembles computers, and the director, Dyachkov Viktor Vasilyevich. He himself is from Tambov, very energetic. How will he meet me, he says: “Farid, when are we going to sell a quantum computer?”
Canadians are already selling. You know about the D-Wave computer, it is periodically tested, Canadians announced that it was first 500 qubits, and now it has 1024 qubits. Periodically during testing, it turns out that all this can be done on a classic computer, then again they have a good quantum computer. But all this is still in this state ...
It can be said that, probably, separate qubits — both 500 and 1024, and further — can be sculpted. But the fact is that a quantum computer will become good and productive, very powerful only if these qubits are in the entangled entangled state. Substantially speaking, this is a situation where the system can be programmed so that the qubits of each other feel. This is almost impossible to do.
If one succeeds in creating such a quantum register — I would not even speak of a quantum computer — where the concatenated states are about 500, this will guarantee such a performance that one can simultaneously work with the states of 2500 . This is the number of particles in the universe, and this is good. Then this system will beat all existing computers.
The Shor algorithm, which is mentioned here, is the first result of 1994. Surely many people know that if Google or Yandex ask what a Quantum algorithm zoo is, then it will immediately roll out a page with more than 50 quantum algorithms that are an order of magnitude better than the existing classical algorithms. There is potentially already a set of algorithms that can be run on quantum machines. And the first is the algorithm Shor, the factorization algorithm. The whole pathos of this business began exactly when Shore's algorithm appeared. Factoring means that the classic RSA algorithms will be beaten by a quantum computer.
In response, this immediately emerged such a trend in the cryptography community - post quantum cryptography. There is such a book, here indicated. In it, the cryptographic community offered a whole set of tools that would deal with a potential quantum computer.
Cryptographers, among other things, talk about such a moment - that, for example, schemes for preparing digital signatures based on hashing, such as the Lamport signature systems, will not be beaten by a quantum computer.

I’ll remember what Lamport’s digital signature is. This is a fairly simple thing, was proposed in 1979. Leslie Lamport is known as the creator of LaTeX, and he is the most quoted person in the field of theoretical and practical computer science. He is prohibitively quoted because he is one of the creators of LaTeX.
Lamport's digital signature is a system that allows the bits, 0 and 1, to be well signed. With 0, a certain word w is associated, with the unit another word v. These are the two private keys for 0 and 1. Alice prepares the value of the functions f (w) and f (v). It is assumed that you need to take a one-way function and send these pairs to Bob. If Alice wants to sign 1, then she sends the source word v and 1 to Bob, and Bob, by quickly calculating the value of f (v) on v, checks if this is really so.
One-sidedness is very grossly informative. This means that it is difficult to find the argument by the value of the function, and the argument is easy to calculate the value of the function. Based on it, you can do the same with long messages ...

The next step, which will be useful to us: we recall what an epsilon-universal hash family is.
Take a set of N hash functions. By a hash function, we mean a function that compresses words of length K into words of length M. K> M, collisions are possible here — situations where two different words are displayed in one word. This happens when K> M.
Let's collect a set of such hash functions. F will be called epsilon-universal, if the following holds: in a situation where f is chosen equiprobably from this set, the probability that two different words will give the same image will be small — no more epsilon. This family is called an epsilon-universal hash family. And in the case when epsilon is 1 / N, this is a universal family.

Using the epsilon-universal hash-family, digital signature systems can be arranged. I will not dwell on this in detail. I will talk about the mathematical part, tell you where it is implemented and what kind of community they work in Russia.

The central idea: we generalize the notion of hashing and hash families of functions to the quantum case. And the essence is this: we will display words in quantum states, in the ensemble qubit. At the same time, we want these two requirements to be fulfilled so that collisions are rare. That is, meaningfully, the slightest change in the words of the argument should lead to a significant change in the hash of the image. It is required in the classics. And of course, the function should be one-way.
As for one-sidedness, I jumped to the classics. The concept of a one-way function, roughly speaking, is related to the problem P ≠ NP. If this condition is fulfilled, then a one-way function exists, and otherwise we work with potentially one-way functions. There is such a problem, we all know about it.

We propose a construction that, in a certain sense, allows us to construct optimal hash functions. We propose a construction that, using classical error-correcting codes, allows us to construct entire families of various quantum hash functions. This is a contribution to post-quantum cryptography.
If Shor’s algorithm fights with classics, here the quantum part allows, in a sense, to intensify the fight against a future quantum computer.

Very briefly what a qubit is here. A qubit is a unit vector in a two-dimensional Hilbert complex space with the property that the coordinates of the vector a 0 and a 1 are complex numbers whose sum of squares of amplitudes equals one. In fact, a complex number is two-dimensional. And, formally speaking, this is a four-dimensional point. But this ratio reduces the dimension to unity, and as a result, a qubit can be represented as a vector in three-dimensional space.
Moreover, this means that he has two degrees of freedom: angle ψ and angle Θ. Everything happens in polar coordinates. This component is called the amplitude of the real, where the sine. And this is called the phase - e iφ .
a 0 and a 1 are the probabilities that we are either at zero or at one if we measure the qubit.
In a sense, a good qubit analogy is a situation where we took a coin, threw it up, and while it flies, it is simultaneously at 0 and 1. It fell, we measured it, the classical probabilistic bit stopped living and manifested either as 0, or as 1. You can throw two coins, but then they will be independent. And a system of quantum bits, if they are concatenated, is something that has no analogue in the classics.

How can you encode a word with one qubit? We interpret the binary word as a number. We are talking only about real parts, there is no phase part. It is clear that if ψ (w) is such a number, and if we consider it as a number modulo 2 k , then the word is encoded into a certain unit vector defined by an angle depending on the word that we read. Everything is normal here. Here's a way to encode the word in one qubit.
This means that physically this encoding is a one-way function. There is the result of Alexander Semenovich Holevo - he works at the Steklov Institute. In the late 1960s, he showed that if we have a qubit ensemble, then the maximum of classical information that can be extracted from an S qubit is S bits. I speak very meaningfully, on the fingers. Behind this are clear wording.
So, if we have one qubit and thus have driven a word there, then from the words of length K we can extract only 1 bit of classic information. This is precisely physical unilateralism. Here two words are encoded in different states, such is the information.
What is wrong here? Two different words may be encoded in similar states, may seem indistinguishable. One qubit is not enough.

Everything I said can be rewritten in the language of the phase. Now we will not talk about real amplitudes, but take the first part, the vector with amplitude 0, the second with amplitude 1, but here we will add a phase. With the help of the phase you can work, but here it is not useful to us.
How can this be implemented? How can one qubit be configured this way? In fact, all transformations are turns, they are unitary. We start with the zero state and, reading at each step the next bit ...

R1, R2 and so on need to specify different. The angles are different. Slowly we gather angles and as a result we get what we need.
Already having a good one-way quantum function, how could we have Lamport's signature translate and do it quantum?
As before, we choose the word w, associate it with 0, and associate the word v with 1. These are secret keys for 0 and 1. And - we collect public keys. These are already quantum states corresponding to the word w: I showed how you can type it on one qubit. The word v is typed in the same way.

We send 0 and the corresponding value of the quantum state 1 to Bob. The process cannot be reversed due to the result of Caleb. Then, if we want, we send Bob a couple of words v and 1. Bob, having the corresponding state and the word v, can verify whether the quantum state ψ (v) was obtained exactly by means of this word. We offer here a reverse test.

Since the transformation is unitary, that is, one-to-one ... There is a word w, a quantum state is prepared, we start from scratch, we apply a unitary transformation, we accumulate the necessary transformation. It turned out the corresponding state. Now that we have received the word w, Bob, knowing the algorithm, can organize this inverse transformation. It's easy to do. And he applies this transformation to the obtained quantum state. As a result, if two words are the same, the result should be state 0.
We know how to compare. If the words are equal, then the reverse test and the corresponding probability that they are equal are determined by the following formula: the scalar product of the vector 0 and the inverse transform state that we received.
If two words are the same, it is always 1 - here we will not be mistaken. And if the states are not equal, then, dealing with only one qubit, we can still be close to unity. This is the case if the two states, ψ (v) and ψ (w), were close.
We need to come up with a situation where two different words would translate the state into almost orthogonal to it. It will be optimal for us.

The next step is when we lack one qubit and we need a register from S qubit.

From one qubit we can go to such a system. This means that we work in a Hilbert space of size 2s and the corresponding ensemble is described in the same way as in the case of a single qubit. a i is amplitude, complex numbers. The norm of this vector is still 1. The norms of these numbers in the square are the probability to get one of the basic states i, if we measure it.
That is, we can say that now we will consider the functions that are arranged as follows: words of length K are mapped into an ensemble of S qubit. The record will be like this.

I will not say how it was organized: this can be done by analogy with how it was done for a single qubit.

The result is now. What will we demand? We will call the function ψ, which maps words of length k into an ensemble of S qubit, δ-Resistant (| Σ k |, s) -quantum function - if the condition is satisfied that two different words of length k generate a state that is almost orthogonal, delta -ortogonal.
This situation will provide the following condition. If we then, for verification, begin to apply the so-called reverse test to them, will it be true that the two states are the same? The likelihood that we say yes is no more than a delta square for different words. If the words are the same, then we will say “yes” with a probability of 1. This is exactly what we need.
The theorem is proved quite simply. It turns out that if we want to build such δ-Resistant (| Σ k |, s) -quantum functions, then s cannot be less than log (k) - log (log (1 + √ (2/1 - δ )) ) - one.
There is a lower score. Is it possible to build such good delta-stable quantum functions that are close to the theoretical lower bound? Surprisingly, it turns out - it is possible.

Looking ahead, I declare a result that says that if we have an error-correcting linear code that is designed so that words of length k are encoded by words of length n and we work in the appropriate field F q , then we can for any preselected δ and for such Δ, which is related to the characteristics of this code d from the Hamming distance n, construct the code length. At the same time, the number of qubit that we need for this is no more than log (n).

Running forward again, we realized the result, looked at how it would look on the very beautiful Reed-Solomon code. And it turned out that the following characteristics are obtained for it. If the length of the code by a constant is greater than the length of the original message, then for such an error threshold as k-1 / q + Θ, we can build the corresponding quantum hash code with the characteristics log (q log (q)) and some sort of overhang. And this thing is quite close to the lower estimate, which is present here.
It was awesome for us. When I told this at a seminar at the Institute of Physics and Technology, Alexander Semenovich Holevo, hearing the lower assessment, said: true, yes, but how to design? When we discussed with him the option that this, for example, can be done using the Reed-Solomon code, he agreed that it was possible to do something in this direction.

This is a description of the report that is presented here. And now I will talk about this in a little more detail ...
The first example was this: we have the word, hash it into one quantum bit. Now it is necessary, having an ensemble of s qubit, to determine how to encode and hash it all. What kind of mechanism should this be? To answer this question, we propose the concept of a quantum hash generator.
First examples. As always, it turns out that there was something in the world, but it was spoken a little in another language. There was such a thing as quantum fingerprinting or quantum fingerprints. This was done in 2002 by Harry Boorman and co-authors for a special communication model of calculation with the arbiter. And it turned out that this is a special binary case of quantum hashing.
One of the tasks in coding theory is to move from binary codes to more than a binary alphabet. Reed-Solomon codes are not fundamentally binary, the game is of high quality. When we go to the field of another characteristic, more than 2, then it really moves here.
I will show the first examples of what has been done. And then I will show you how to switch from error correcting codes and invest in this design.

There is an epsilon-universal hash family. Using a certain family of functions, I will begin to generate one quantum function. There is a set of classical linear functions, there is a field F q . From it we take the coefficients and have a set of functions H = {h 1 , ..., h T }. Now, with the help of the function h, we generate single-qubit quantum functions in this way. For simplicity, I will not work with phases, but with real amplitudes. In a sense, it is intuitively clear, although physicists for their realization asked to rewrite it all into a phase language, because the phase thing is easier to implement.
Now we prepare a set of such quantum functions: | ψ h j (w)⟩ = cos 2πh j (w) / q | 0⟩ + sin 2πh j (w) / q | 1⟩.
Then we assemble these functions into one like this: | ψ H (w) = 1 / √T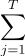 | j⟩ | ψ h j (w)⟩.
| j⟩ | ψ h j (w)⟩.
In essence, this record means that we simultaneously run the computation of all these T-functions h equally or equally probable. And we build calculations in this way - quantum physics allows us to do this. Before us is a mathematical record of what physics allows you to do.
Register j must be interpreted as a binary record of j. And if so, then we only need to have a log (T) bit, they correspond to the state of the qubit. I will not speak in detail how this is done. And log (T) qubit directs the calculation of the last qubit. — . T — log(T) .

, , , . d, k n, , .
log(n) . — , E i (w). — , 90 . , 90 . log(n+1) , .
, , . , . - k, s s . .

. 2009 , , . , , . . , , , , 1993 . , , log(q) : T = ⎡( 2 / δ 2 ) ln(2q)⎤.
, log(k), -. -, q, log(k), s .

, : -. , G — - . - l , , , -, - , k d+l -, — -.

ó, 2008 .
-, -. , - -. .

— , . : - -, , N , k F q . : - — . , -, .
, F, . - . -, k s . Δ ≦ ε + δ — - - - - -, . - -.
. , - , .

, , computer science. , , 1979 , « fingerprinting», , . . , , p i . , p i .
« » 70-80- , , .

, , , - , 1/- , — . - -, , , , , , , fingerprinting - : -, k s . : — , 1/ — , — . . , .
-, , , , . , — -.

. - 1979-1980- — -. .
, , , . Here it is. . -, - . , — . , — , .

, . — log(k), — k. , , .

, . nkd, k n, F q , -. , -, , Δ = (1 – d/n) + δ. , , δ — , . s, , : s ≦ log(n) + log(log(q)) + 2*log(1/δ) + 4.
1994 , , , , , -. : - , , .
- 70-80- . , — , , : 50-60- . , 1994 . , , — . It will be interesting.

, - — , — -, -.

, . .
, . A lot of them. , , -. , . - — , , . - — . .

. , .

. . , , , — .
? . , . , . , , . .
, , . . 100 , , . 100 , , . , — .
, , . — . ? , , . , , , , -.
, s 10, ? s 100? , , , . s 100 , -, — ?
, . . , … , . , . , .
, , . - . , . , , , — , . , . .
, . , , . « » . , , . . , . , . -84, -. 1984 , : .
, . , , , , , .
, . , .
, , , , , . .
, . Thank.
— ?
— . , -84 — , . , . -84 , . , , , — -.
. , . , — , . : , , - . . , . , . , -84, . , - .
— , , , , . ? , , .
— , . — . — , computer science. , , . , computer science — , , . . .
, , .
MIT. , , .
— . — . , . , , . , — , , — . , ! : . . — . , , .
, . , , — . , — - , . , . , .
? . : - , - principal investigator , . , . — , . . .
— . , Computer Science in Russia, . , scottaaronson.com/blog. , , . , . Quantum Computing since Democritus, « ». , .
— , , brain module - , NPPO- . , . , . , complexity zoo — . , . .
Thank.
One of the areas where significant changes can occur with the advent of quantum systems is digital signature mechanisms. The report reveals a hashing algorithm that radically exceeds analogs for classic computers. Under the cut - a detailed transcript and slides.
Most of the slides will be in English, but I think my colleagues will excuse me. It is not always possible to translate everything, well, there is not always a need.
')

This report is based on the works that are presented here. With our first work - I myself am a mathematician - we were invited to the journal Laser Physics Letters, which, unlike the high-ranking mathematical journals, with the corresponding index slightly less than 1, has an index of 3.2. Now, when all Hirsch Indices and others are taken into account, it turns out to be useful to publish in such journals - physical ones.
One of the latest results was published at the seminar Algebra in Computational Complexity, there is such a German center. These results can be seen there. Archive is understandable.

I'll start with motivation. Daniel joked that soon there will be a quantum computer, and we will all use it. In Kazan, there is a group that assembles computers, and the director, Dyachkov Viktor Vasilyevich. He himself is from Tambov, very energetic. How will he meet me, he says: “Farid, when are we going to sell a quantum computer?”
Canadians are already selling. You know about the D-Wave computer, it is periodically tested, Canadians announced that it was first 500 qubits, and now it has 1024 qubits. Periodically during testing, it turns out that all this can be done on a classic computer, then again they have a good quantum computer. But all this is still in this state ...
It can be said that, probably, separate qubits — both 500 and 1024, and further — can be sculpted. But the fact is that a quantum computer will become good and productive, very powerful only if these qubits are in the entangled entangled state. Substantially speaking, this is a situation where the system can be programmed so that the qubits of each other feel. This is almost impossible to do.
If one succeeds in creating such a quantum register — I would not even speak of a quantum computer — where the concatenated states are about 500, this will guarantee such a performance that one can simultaneously work with the states of 2500 . This is the number of particles in the universe, and this is good. Then this system will beat all existing computers.
The Shor algorithm, which is mentioned here, is the first result of 1994. Surely many people know that if Google or Yandex ask what a Quantum algorithm zoo is, then it will immediately roll out a page with more than 50 quantum algorithms that are an order of magnitude better than the existing classical algorithms. There is potentially already a set of algorithms that can be run on quantum machines. And the first is the algorithm Shor, the factorization algorithm. The whole pathos of this business began exactly when Shore's algorithm appeared. Factoring means that the classic RSA algorithms will be beaten by a quantum computer.
In response, this immediately emerged such a trend in the cryptography community - post quantum cryptography. There is such a book, here indicated. In it, the cryptographic community offered a whole set of tools that would deal with a potential quantum computer.
Cryptographers, among other things, talk about such a moment - that, for example, schemes for preparing digital signatures based on hashing, such as the Lamport signature systems, will not be beaten by a quantum computer.

I’ll remember what Lamport’s digital signature is. This is a fairly simple thing, was proposed in 1979. Leslie Lamport is known as the creator of LaTeX, and he is the most quoted person in the field of theoretical and practical computer science. He is prohibitively quoted because he is one of the creators of LaTeX.
Lamport's digital signature is a system that allows the bits, 0 and 1, to be well signed. With 0, a certain word w is associated, with the unit another word v. These are the two private keys for 0 and 1. Alice prepares the value of the functions f (w) and f (v). It is assumed that you need to take a one-way function and send these pairs to Bob. If Alice wants to sign 1, then she sends the source word v and 1 to Bob, and Bob, by quickly calculating the value of f (v) on v, checks if this is really so.
One-sidedness is very grossly informative. This means that it is difficult to find the argument by the value of the function, and the argument is easy to calculate the value of the function. Based on it, you can do the same with long messages ...

The next step, which will be useful to us: we recall what an epsilon-universal hash family is.
Take a set of N hash functions. By a hash function, we mean a function that compresses words of length K into words of length M. K> M, collisions are possible here — situations where two different words are displayed in one word. This happens when K> M.
Let's collect a set of such hash functions. F will be called epsilon-universal, if the following holds: in a situation where f is chosen equiprobably from this set, the probability that two different words will give the same image will be small — no more epsilon. This family is called an epsilon-universal hash family. And in the case when epsilon is 1 / N, this is a universal family.

Using the epsilon-universal hash-family, digital signature systems can be arranged. I will not dwell on this in detail. I will talk about the mathematical part, tell you where it is implemented and what kind of community they work in Russia.

The central idea: we generalize the notion of hashing and hash families of functions to the quantum case. And the essence is this: we will display words in quantum states, in the ensemble qubit. At the same time, we want these two requirements to be fulfilled so that collisions are rare. That is, meaningfully, the slightest change in the words of the argument should lead to a significant change in the hash of the image. It is required in the classics. And of course, the function should be one-way.
As for one-sidedness, I jumped to the classics. The concept of a one-way function, roughly speaking, is related to the problem P ≠ NP. If this condition is fulfilled, then a one-way function exists, and otherwise we work with potentially one-way functions. There is such a problem, we all know about it.

We propose a construction that, in a certain sense, allows us to construct optimal hash functions. We propose a construction that, using classical error-correcting codes, allows us to construct entire families of various quantum hash functions. This is a contribution to post-quantum cryptography.
If Shor’s algorithm fights with classics, here the quantum part allows, in a sense, to intensify the fight against a future quantum computer.

Very briefly what a qubit is here. A qubit is a unit vector in a two-dimensional Hilbert complex space with the property that the coordinates of the vector a 0 and a 1 are complex numbers whose sum of squares of amplitudes equals one. In fact, a complex number is two-dimensional. And, formally speaking, this is a four-dimensional point. But this ratio reduces the dimension to unity, and as a result, a qubit can be represented as a vector in three-dimensional space.
Moreover, this means that he has two degrees of freedom: angle ψ and angle Θ. Everything happens in polar coordinates. This component is called the amplitude of the real, where the sine. And this is called the phase - e iφ .
a 0 and a 1 are the probabilities that we are either at zero or at one if we measure the qubit.
In a sense, a good qubit analogy is a situation where we took a coin, threw it up, and while it flies, it is simultaneously at 0 and 1. It fell, we measured it, the classical probabilistic bit stopped living and manifested either as 0, or as 1. You can throw two coins, but then they will be independent. And a system of quantum bits, if they are concatenated, is something that has no analogue in the classics.

How can you encode a word with one qubit? We interpret the binary word as a number. We are talking only about real parts, there is no phase part. It is clear that if ψ (w) is such a number, and if we consider it as a number modulo 2 k , then the word is encoded into a certain unit vector defined by an angle depending on the word that we read. Everything is normal here. Here's a way to encode the word in one qubit.
This means that physically this encoding is a one-way function. There is the result of Alexander Semenovich Holevo - he works at the Steklov Institute. In the late 1960s, he showed that if we have a qubit ensemble, then the maximum of classical information that can be extracted from an S qubit is S bits. I speak very meaningfully, on the fingers. Behind this are clear wording.
So, if we have one qubit and thus have driven a word there, then from the words of length K we can extract only 1 bit of classic information. This is precisely physical unilateralism. Here two words are encoded in different states, such is the information.
What is wrong here? Two different words may be encoded in similar states, may seem indistinguishable. One qubit is not enough.

Everything I said can be rewritten in the language of the phase. Now we will not talk about real amplitudes, but take the first part, the vector with amplitude 0, the second with amplitude 1, but here we will add a phase. With the help of the phase you can work, but here it is not useful to us.
How can this be implemented? How can one qubit be configured this way? In fact, all transformations are turns, they are unitary. We start with the zero state and, reading at each step the next bit ...

R1, R2 and so on need to specify different. The angles are different. Slowly we gather angles and as a result we get what we need.
Already having a good one-way quantum function, how could we have Lamport's signature translate and do it quantum?
As before, we choose the word w, associate it with 0, and associate the word v with 1. These are secret keys for 0 and 1. And - we collect public keys. These are already quantum states corresponding to the word w: I showed how you can type it on one qubit. The word v is typed in the same way.

We send 0 and the corresponding value of the quantum state 1 to Bob. The process cannot be reversed due to the result of Caleb. Then, if we want, we send Bob a couple of words v and 1. Bob, having the corresponding state and the word v, can verify whether the quantum state ψ (v) was obtained exactly by means of this word. We offer here a reverse test.

Since the transformation is unitary, that is, one-to-one ... There is a word w, a quantum state is prepared, we start from scratch, we apply a unitary transformation, we accumulate the necessary transformation. It turned out the corresponding state. Now that we have received the word w, Bob, knowing the algorithm, can organize this inverse transformation. It's easy to do. And he applies this transformation to the obtained quantum state. As a result, if two words are the same, the result should be state 0.
We know how to compare. If the words are equal, then the reverse test and the corresponding probability that they are equal are determined by the following formula: the scalar product of the vector 0 and the inverse transform state that we received.
If two words are the same, it is always 1 - here we will not be mistaken. And if the states are not equal, then, dealing with only one qubit, we can still be close to unity. This is the case if the two states, ψ (v) and ψ (w), were close.
We need to come up with a situation where two different words would translate the state into almost orthogonal to it. It will be optimal for us.

The next step is when we lack one qubit and we need a register from S qubit.

From one qubit we can go to such a system. This means that we work in a Hilbert space of size 2s and the corresponding ensemble is described in the same way as in the case of a single qubit. a i is amplitude, complex numbers. The norm of this vector is still 1. The norms of these numbers in the square are the probability to get one of the basic states i, if we measure it.
That is, we can say that now we will consider the functions that are arranged as follows: words of length K are mapped into an ensemble of S qubit. The record will be like this.

I will not say how it was organized: this can be done by analogy with how it was done for a single qubit.

The result is now. What will we demand? We will call the function ψ, which maps words of length k into an ensemble of S qubit, δ-Resistant (| Σ k |, s) -quantum function - if the condition is satisfied that two different words of length k generate a state that is almost orthogonal, delta -ortogonal.
This situation will provide the following condition. If we then, for verification, begin to apply the so-called reverse test to them, will it be true that the two states are the same? The likelihood that we say yes is no more than a delta square for different words. If the words are the same, then we will say “yes” with a probability of 1. This is exactly what we need.
The theorem is proved quite simply. It turns out that if we want to build such δ-Resistant (| Σ k |, s) -quantum functions, then s cannot be less than log (k) - log (log (1 + √ (2/1 - δ )) ) - one.
There is a lower score. Is it possible to build such good delta-stable quantum functions that are close to the theoretical lower bound? Surprisingly, it turns out - it is possible.

Looking ahead, I declare a result that says that if we have an error-correcting linear code that is designed so that words of length k are encoded by words of length n and we work in the appropriate field F q , then we can for any preselected δ and for such Δ, which is related to the characteristics of this code d from the Hamming distance n, construct the code length. At the same time, the number of qubit that we need for this is no more than log (n).

Running forward again, we realized the result, looked at how it would look on the very beautiful Reed-Solomon code. And it turned out that the following characteristics are obtained for it. If the length of the code by a constant is greater than the length of the original message, then for such an error threshold as k-1 / q + Θ, we can build the corresponding quantum hash code with the characteristics log (q log (q)) and some sort of overhang. And this thing is quite close to the lower estimate, which is present here.
It was awesome for us. When I told this at a seminar at the Institute of Physics and Technology, Alexander Semenovich Holevo, hearing the lower assessment, said: true, yes, but how to design? When we discussed with him the option that this, for example, can be done using the Reed-Solomon code, he agreed that it was possible to do something in this direction.

This is a description of the report that is presented here. And now I will talk about this in a little more detail ...
The first example was this: we have the word, hash it into one quantum bit. Now it is necessary, having an ensemble of s qubit, to determine how to encode and hash it all. What kind of mechanism should this be? To answer this question, we propose the concept of a quantum hash generator.
First examples. As always, it turns out that there was something in the world, but it was spoken a little in another language. There was such a thing as quantum fingerprinting or quantum fingerprints. This was done in 2002 by Harry Boorman and co-authors for a special communication model of calculation with the arbiter. And it turned out that this is a special binary case of quantum hashing.
One of the tasks in coding theory is to move from binary codes to more than a binary alphabet. Reed-Solomon codes are not fundamentally binary, the game is of high quality. When we go to the field of another characteristic, more than 2, then it really moves here.
I will show the first examples of what has been done. And then I will show you how to switch from error correcting codes and invest in this design.

There is an epsilon-universal hash family. Using a certain family of functions, I will begin to generate one quantum function. There is a set of classical linear functions, there is a field F q . From it we take the coefficients and have a set of functions H = {h 1 , ..., h T }. Now, with the help of the function h, we generate single-qubit quantum functions in this way. For simplicity, I will not work with phases, but with real amplitudes. In a sense, it is intuitively clear, although physicists for their realization asked to rewrite it all into a phase language, because the phase thing is easier to implement.
Now we prepare a set of such quantum functions: | ψ h j (w)⟩ = cos 2πh j (w) / q | 0⟩ + sin 2πh j (w) / q | 1⟩.
Then we assemble these functions into one like this: | ψ H (w) = 1 / √T
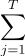 | j⟩ | ψ h j (w)⟩.
| j⟩ | ψ h j (w)⟩.In essence, this record means that we simultaneously run the computation of all these T-functions h equally or equally probable. And we build calculations in this way - quantum physics allows us to do this. Before us is a mathematical record of what physics allows you to do.
Register j must be interpreted as a binary record of j. And if so, then we only need to have a log (T) bit, they correspond to the state of the qubit. I will not speak in detail how this is done. And log (T) qubit directs the calculation of the last qubit. — . T — log(T) .

, , , . d, k n, , .
log(n) . — , E i (w). — , 90 . , 90 . log(n+1) , .
, , . , . - k, s s . .

. 2009 , , . , , . . , , , , 1993 . , , log(q) : T = ⎡( 2 / δ 2 ) ln(2q)⎤.
, log(k), -. -, q, log(k), s .

, : -. , G — - . - l , , , -, - , k d+l -, — -.

ó, 2008 .
-, -. , - -. .

— , . : - -, , N , k F q . : - — . , -, .
, F, . - . -, k s . Δ ≦ ε + δ — - - - - -, . - -.
. , - , .

, , computer science. , , 1979 , « fingerprinting», , . . , , p i . , p i .
« » 70-80- , , .

, , , - , 1/- , — . - -, , , , , , , fingerprinting - : -, k s . : — , 1/ — , — . . , .
-, , , , . , — -.

. - 1979-1980- — -. .
, , , . Here it is. . -, - . , — . , — , .

, . — log(k), — k. , , .

, . nkd, k n, F q , -. , -, , Δ = (1 – d/n) + δ. , , δ — , . s, , : s ≦ log(n) + log(log(q)) + 2*log(1/δ) + 4.
1994 , , , , , -. : - , , .
- 70-80- . , — , , : 50-60- . , 1994 . , , — . It will be interesting.

, - — , — -, -.

, . .
, . A lot of them. , , -. , . - — , , . - — . .

. , .

. . , , , — .
? . , . , . , , . .
, , . . 100 , , . 100 , , . , — .
, , . — . ? , , . , , , , -.
, s 10, ? s 100? , , , . s 100 , -, — ?
, . . , … , . , . , .
, , . - . , . , , , — , . , . .
, . , , . « » . , , . . , . , . -84, -. 1984 , : .
, . , , , , , .
, . , .
, , , , , . .
, . Thank.
— ?
— . , -84 — , . , . -84 , . , , , — -.
. , . , — , . : , , - . . , . , . , -84, . , - .
— , , , , . ? , , .
— , . — . — , computer science. , , . , computer science — , , . . .
, , .
MIT. , , .
— . — . , . , , . , — , , — . , ! : . . — . , , .
, . , , — . , — - , . , . , .
? . : - , - principal investigator , . , . — , . . .
— . , Computer Science in Russia, . , scottaaronson.com/blog. , , . , . Quantum Computing since Democritus, « ». , .
— , , brain module - , NPPO- . , . , . , complexity zoo — . , . .
Thank.
Source: https://habr.com/ru/post/312072/
All Articles