Arrows as an approach to representing systems in Java

Often there is a description of systems, algorithms and processes in the form of structural schemes. Therefore, the task of presenting structural diagrams, for example, from technical documentation or a specification in a programming language, is relevant.

The article discusses the approach to the presentation of structural schemes using the concept of arrows, described by John Hughes and used in Haskell in the Yampa and Netwire FRP frameworks, as well as in the Haskell XML Toolbox .

A feature of structural schemes is a visual representation of the sequence of operations (blocks) without focusing on the data itself (variables) themselves and their states. For example, consider a direct gain radio.

How to implement this method of describing systems and computing within the existing mainstream programming languages?

A traditional description of such a scheme in a C-like programming language would look something like this.

//    Antenna antenna = new Antenna(Ether.getInstance()); Filter filter1 = new Filter(5000); //  -   Filter filter2 = new Filter(5000); Filter filter3 = new Filter(5000); Detector detector = new Detector("AM"); //   -  Amplifier amp = new Amplifier(5); //   Speaker speaker = new Speaker(10); //  Signal inputSignal = antenna.receive(); //     Signal filter1Res = filter1.filter(inputSignal); Signal filter2Res = filter2.filter(filter1Res); Signal filter3Res = filter3.filter(filter2Res); Signal detected = detector.detect(filter3Res); Signal amplified = amp.amplify(detected); speaker.speak(amplified); 

It can be seen that variables were added to the program that are not in the structural diagram, and which, therefore, do not add any information about the operation of the radio receiver, but are only needed to store intermediate results of processing the input signal.

Such a program, which describes only a simple phased passage of a signal through processing units, looks rather cumbersome. A more concise approach would be to describe the scheme using the new join method, which connects the blocks to each other:

 Receiver receiver = Receiver.join(filter1).join(filter2).join(filter3) .join(detector).join(amp).join(speaker); receiver.apply(antenna.receive()); 

The join() method describes a sequential connection of blocks, that is, a.join(b) means that the result of processing by block a will be passed to the input of block b . All that is required is that the connectable Filter , Amplifier , Detector , Speaker classes additionally implement the apply() method, which performs the “default action” (for Filter — filter() , for Amplifier — amplify() , etc.), and allowing to call an object as a function.

With a functional approach, these classes would be functions that return functions, so that we would not even have to create instances of classes and the whole program would look something like this:

 Receiver receiver = Receiver.join(filter(5000)).join(filter(5000)).join(filter(5000)) .join(detector("AM")).join(amplifier(5)).join(speaker(10)); receiver.apply(antenna.receive()); 

Arrows as a way to describe calculations

A feature of the functional approach is the use of combinators (for example, monads), which are functions that combine other functions into composite calculations.

The arrows are also a combinator and allow generalized description of composite calculations. This article uses the jArrows arrows implementation , written in Java 8.

What is an arrow

The arrow Arrow<In, Out> a of the function Out f(In x) represents the calculation that is performed by the function f . As you might have guessed, In is the type of the input value of the arrow (taken by the function f ), Out is the type of the output value (returned by the function f ). The advantage of presenting calculations in the form of arrows is the possibility of explicitly combining calculations in various ways.

For example, the calculation y = x * 5.0 , in Java, represented by the function

 double multBy5_0(int in) { return in*5.0; } 

can be represented as an arrow

 Arrow<Integer, Double> arrMultBy5_0 = Action.of(multBy5_0); 

Further, the calculation packed into an arrow can be combined with other calculations-arrows. The Action class is one of the implementations of the Arrow interface. Another implementation of this interface is ParallelAction , which supports multi-thread computing.

Arrow composition

The arrMultBy5_0 can be connected in series with another arrow — for example, adding 10.5 to an input value, and then with the next arrow, representing the result as a string. It turns out a chain of arrows

 Arrow<Integer, String> mult5Plus10toStr = arrMultBy5_0.join(in -> in+10.5) .join(in -> String.valueOf(in)); mult5Plus10toStr.apply(10); // "60.5" 

The resulting calculation, represented by the mult5Plus10toStr composite arrow, can be represented as a structural diagram:

The input of this arrow is of type Integer (the input type is the first calculation in the chain), and the output is of type String (the output type is the last calculation in the chain).

The someArrow.join(g) method someArrow.join(g) calculation represented by the someArrow arrow with the calculation represented by g , while g can be another arrow, a lambda function, a method, or something else that the Applicable interface implements with the apply(x) , which can be applied to the input value x .

 class Action<In, Out> implements Arrow<In, Out>, Applicable<In, Out> { Applicable<In, Out> func; public Arrow<In, OutB> join(Applicable<Out, OutB> b) { return Action.of(i -> b.apply(this.func.apply(i))); } } 

Other Arrow Compositions

In addition to the serial connection using the join method, arrows can be connected in parallel using the combine , cloneInput and split methods. An example of using the combine method to describe the calculation of sin(x)^2+cos(x)^2

 Arrow<Pair<Double, Double>, Pair<Double, Double>> sin_cos = Action.of(Math::sin).combine(Math::cos); Arrow<Double, Double> sqr = Action.of(i -> i*i); Arrow<Pair<Double, Double>, Double> sum_SinCos = sin_cos.join(sqr.combine(sqr)) .join(p -> p.left + p.right); sum_SinCos.apply(Pair.of(0.7, 0.2)); // 1.38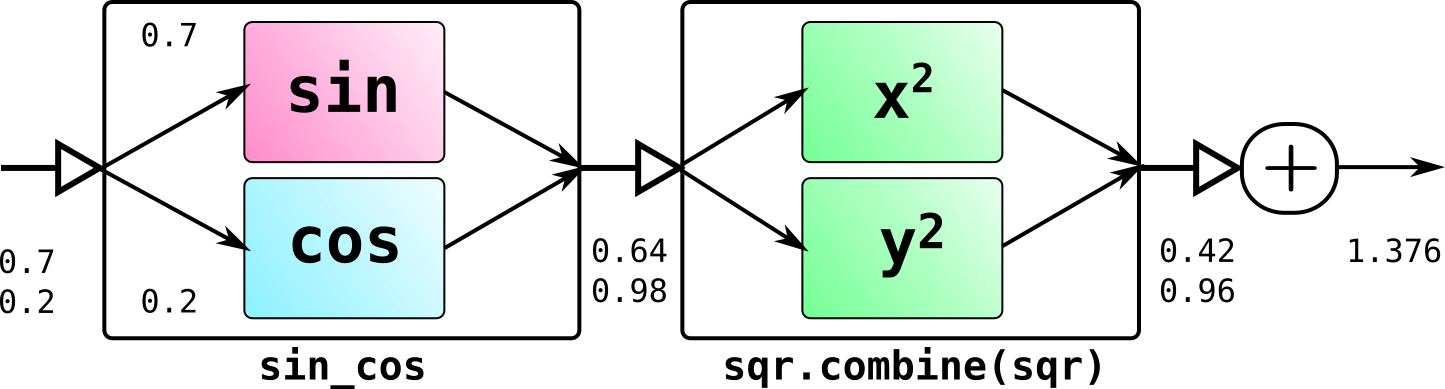 

The resulting "wide" arrow sin_cos takes as input a pair of Pair<Double, Double> values, the first value of the pair.left pair goes to the input of the first arrow (sin function), the second pair.right to the input of the second arrow (cos function), the results are also paired up. The next compound arrow, sqr.combine(sqr) accepts a Pair<Double, Double> value Pair<Double, Double> as an input and squads both values ​​of the pair. The last arrow summarizes the result.

The method someArrow.cloneInput(f) creates an arrow, in parallel connecting someArrow and f and applying them to the input, its output is represented as a pair uniting the results of the calculations of these arrows. The input types someArrow and f must match.

 Arrow<Integer, Pair<Integer, Double>> sqrAndSqrt = Action.of((Integer i) -> i*i) .cloneInput(Math::sqrt); sqrAndSqrt.apply(5); // Pair(25, 2.236)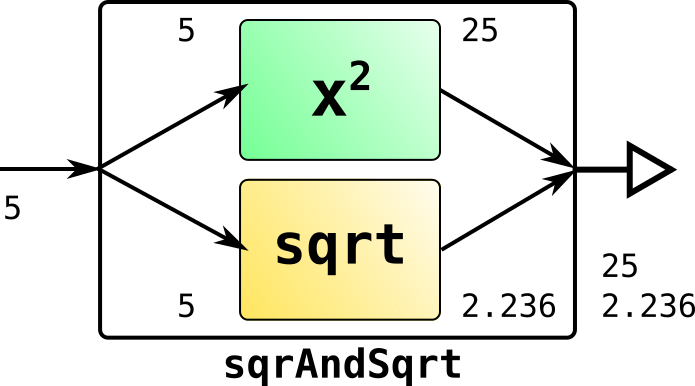 

Parallel connection in this case means that the results of two calculations connected in parallel are independent of each other - in contrast to a serial connection by the join method, when the result of one calculation is passed to the input of the other. Multi-threaded parallel connections are implemented by the ParallelAction class.

The someArrow.split(f, g) method is an optional method equivalent to someArrow.join(f.cloneInput(g)) . The result of the calculation someArrow parallel transmitted to the input f and g , the output of such an arrow will be a pair with the results of the calculations f and g .

Computation bypass

Sometimes you need to pass a portion of the input value of the arrow further along the chain along with the result of the calculation. This is implemented by the method someArrow.first() and supplementing it with someArrow.second() , which transforms the arrow of someArrow so that the resulting arrow takes a pair of values ​​as input and applies the calculation to only one of the elements of this pair

 Arrow<Integer, Double> arr = Action.of(i -> Math.sqrt(i*i*i)); Pair input = Pair.of(10, 10); arr.<Integer>first().apply(Pair.of(10, 10))); // Pair(31.623, 10) arr.<Integer>second().apply(Pair.of(10, 10))); // Pair(10, 31.623) 

These methods are similar to the someArrow.bypass2nd() and someArrow.bypass1st() methods, respectively.

Completeness of the description

According to Hughes, the description of any calculation is possible using only three functions:

• 1) A constructor building an arrow from a function (in this implementation Action.of)
• 2) Functions that sequentially connect two arrows (Arrow :: join)
• 2) Functions that apply the calculation to the input part (Arrow :: first)

The jArrows implementation jArrows also been extended with additional methods that simplify the description of systems.

findings

The high-level description of processes in the form of flowcharts is practically not used in the imperative approach to programming. At the same time, such a description fits well with the functional reactive approach, which is becoming more common.

As shown in the Hughes article, the arrows, in essence, are the implementation of the description of systems in the form of flowcharts within the framework of functional programming, are a more generalized description than the monads, which have already become popular in the mainstream, in particular in the form of their implementation in Java This article describes the basic principles of this approach, in the future it is of interest to adapt the existing and develop new patterns for the use of arrows in mainstream software development.