How the use of redundancy codes in SDS helps Yandex keep data cheaply and securely

Yandex, like any other large Internet company, stores a lot, or rather a lot of data. This includes user data from different services, and sites that are inked, and intermediate data for calculating weather, and backup copies of databases. Storage cost ($ / GB) is one of the important indicators of the system. In this article I want to tell you about one of the methods that allowed us to seriously reduce the cost of storage.

In 2015, as you all remember, the dollar rose strongly. More precisely, it began to grow at the end of 2014, but we ordered new batches of iron already in 2015. Yandex earns in rubles, and therefore the cost of iron for us has increased along with the exchange rate. This made us once again think about how to make it possible to put more data into the current cluster. Of course, we do this regularly, but this time the motivation was especially strong.

Each cluster server provides us with the following resources: processor, RAM, hard drives, and the network. The network here is a more complex concept than just a network card. It is also the entire infrastructure inside the data center, and the connectivity between different data centers and traffic exchange points. In a cluster, replication was used to ensure reliability, and the total cluster size was determined solely through the total capacity of the hard drives. It was necessary to figure out how to exchange the remaining resources for an increase in space. By the way, if after the post you still have questions that you would like to discuss in person, come to our meeting .

RAM is difficult to exchange. We use disk shelves, and the difference in the amount of RAM to disk capacity is more than three orders of magnitude. It can be used to speed up access within a single machine, but this is a story for a separate article.

The processor exchanges quite obviously through archiving. But you need to pay attention to several pitfalls. First, the degree of compression is highly dependent on the combination of the archiver and the stored data, that is, you need to take a representative sample of data and estimate how much you will save. Secondly, the archiver should provide the ability to read data from almost any place, otherwise you will have to forget about the Range header in HTTP (and customers with not very good Internet, who will no longer be able to download large files, will be offended by this). Thirdly, the speed of compression and decompression, as well as the associated CPU consumption, are important. You can take an archiver that will compress the data quite effectively, but the number of processors in your cluster is not enough to provide the current write speed. When unpacking, in turn, latency requests will suffer. Not so long ago, Facebook officially released its archiver Zstd - we recommend it to try. It is very fast and compresses data pretty well.

Of all the resources, the network remains, and with it we have a lot of room for creativity. How to exchange the network for storage capacity will be discussed further.

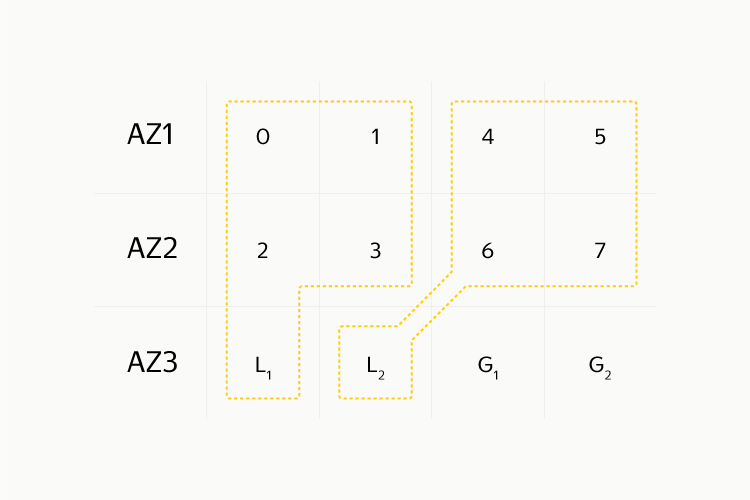
Yandex has quite strict storage requirements. It must remain operational even if one data center is lost entirely. This condition imposes quite strong restrictions on the technologies that can be applied, but in exchange we get higher reliability than from the data center itself. For us as storage system developers, this means that the redundancy factor must be greater than one when any data center drops out.

In general, it is more correct to talk about accessibility zones. In our case, it is the entire data center, but it can be a separate machine, a rack, a machine room, or even a continent. That is, if we have four availability zones and we evenly distribute data between them, then the degree of redundancy cannot be less than 1. (3), 0. (3) in each of the zones. So, there are N availability zones and you need to somehow decompose the data on them.

Replicas

Obviously, the easiest way is to make full replicas. Most often, two or three replicas are made, and for many years we have been living according to this scheme. The disadvantages are obvious: you have to use two (or, respectively, three) gigabytes of hard disk space to store one gigabyte of data. But there are also advantages: a full-fledged file is stored in each replica, it is easy to read, and at the same time it lies entirely on one machine, on one hard disk. Recovering data when a disk is lost is also quite simple - by regular copying over the network.

For the storage of user content, Yandex.Music data, various avatars and other similar data, we are responsible for the MDS - Media Storage service. It is based on Elliptics, Eblob and HTTP proxy. Elliptics provides network routing, Eblob is needed for storing data on a disk, and a proxy is used for terminating user traffic. All this cluster is controlled by a system called Mastermind. In our storage, we departed from the concept of large DHT-rings, which we tried in Elliptics earlier, and divided the entire space into small shards of 916 gigabytes. We call them "drops" (from the English. Couple). The figure 916 is chosen because we need to place a multiple of the number of replicas of the drops on one hard disk (disk manufacturers, in turn, love marketing and consider the volume in decimal terabytes). Mastermind ensures that replicas of a single drop are always located in different DCs, starts the data recovery procedure, defragmentation, and generally automates the work of system administrators.

To restore consistency, we have a special procedure that runs through all the keys and appends the missing keys to those replicas where they are not. This procedure is not very fast, but we run it only where there is a discrepancy in the number of living keys between replicas. Side plus - creates a load on the hard drive, even if the data there is cold and the users behind them do not come. As a result, the disk begins to die in advance, and not at the moment when we are trying to recover the data, having discovered that another replica has already died. We quietly change it, after which the recovery starts automatically and the user data remains safe and sound.

Redundancy codes

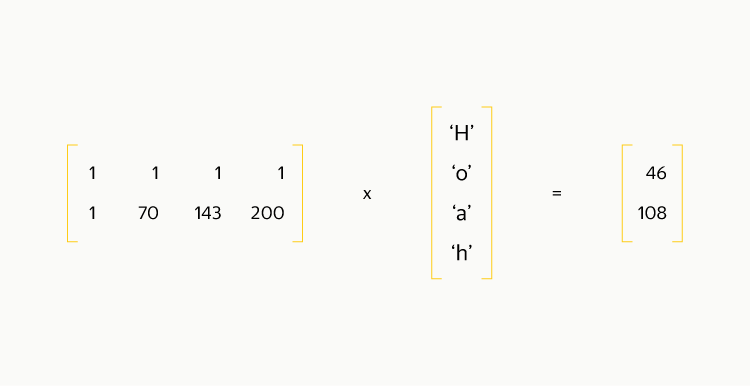
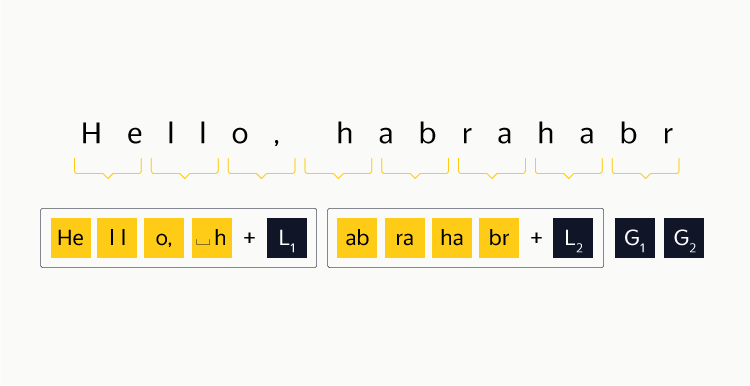
To make an analogy, this kind of data replication is RAID 1, simple, reliable, and not very efficient in terms of space consumption. We want to create something similar to RAID 5 or RAID 6. Again, we go from simple to complex: we take three availability zones, somehow block our data into blocks, write even blocks to availability zone 1, and odd numbers to the second, in the third - the result of a byte XOR between blocks. For error detection, we consider for each block a checksum that is negligible in comparison with the block size. Data recovery is elementary: if a ^ b = c, then b = a ^ c. The redundancy factor with this approach is 1.5. If any block is lost, you will need to read two others, and from different access zones. Recovery is possible with the loss of no more than one disk, which is much worse than in the case of three replicas, and is comparable to two replicas. This is how the XOR result for the string “Hello, habrahabr” is considered (the bottom numbers are the decimal representation of the byte):

Here it is necessary to introduce the concept of stripe. A stripe is N consecutive blocks, and the beginning of the first stripe coincides with the beginning of the data stream, N depends on the selected coding scheme, and in the case of RAID 1 N = 2. To effectively use redundancy codes, you need to combine all files into one continuous stream of bytes, and break it into stripes already. Nearby you should save the markup, in which type and with which byte each file starts, as well as its size. If the length of the data stream is not a multiple of the stripe size, then the rest should be filled with zeros. Schematically, this can be represented as:

')

When choosing a stripe size, you can use the following considerations:

• the larger the block size, the more files will fit in one block and the smaller the readings from the two availability zones at once,
• the larger the block size, the more data must be dragged across the network in the event of a block being temporarily unavailable or lost.

Thus, it is necessary to consider the probabilities of these events. It turned out that the optimal size is two medians of the file size. In addition, it is advisable to re-sort the files so that the block boundaries fall into larger files that would not fit in one block anyway. This will also reduce the load on the network. And to simplify the code, the function of storing parity blocks is assigned to one of the accessibility zones.

Reed-Solomon codes

But what if you want more reliability? Correct - use more powerful redundancy codes. Now one of the most common codes is the Reed-Solomon code. It is used when recording DVDs, in digital TV (DVB-T), in QR codes, and also in RAID 6. We are not going to talk about the mathematics of the Galois fields here - an engineering approach is waiting for you. For all calculations, we will use the jerasure library, which has a difficult fate, but which works very quickly and has all the functions we need.

The first thing worth noting: for an effective result, you need to work in the fields 2 ^ 8, 2 ^ 16, 2 ^ 32, that is, in machine words. Further, for simplicity, we will use the field 2 ^ 8 and work with bytes. To make the example more specific, let's try to achieve a replication ratio of 1.5, but with two parity blocks. To do this, you need to split the data into stripes of 4 blocks each, and generate 2 parity blocks. If we take the first byte from each data block, we can compose a vector of dimension 4 and, similarly, a vector of dimension 2 for parity blocks. In order to get a vector of dimension 2 from a vector of dimension 4, it must be multiplied by a 2x4 coding matrix, and multiplied by the rules of operation in the Galois fields, if viewed from an engineering point of view. The matrix that we need is called the Vandermond matrix. For the selected field, such a matrix guarantees a property similar to the absence of linear combinations in ordinary algebra. When restoring data, it will also play an important role.

Let's take one stripe of data “Hello, habrahabr”. It is very well divided into 4 blocks of 4 bytes each, with one byte corresponding to one encoding word.

So, it turns out the following picture:

We calculate the parity blocks in this way, word by word (in our case - byte by byte).

If you slightly change the picture and add the identity matrix above the coding matrix, then the output data will appear in the output vector:

Suppose we have lost block number 2 and block number 4. Delete the corresponding rows from the matrix and from the right vector:

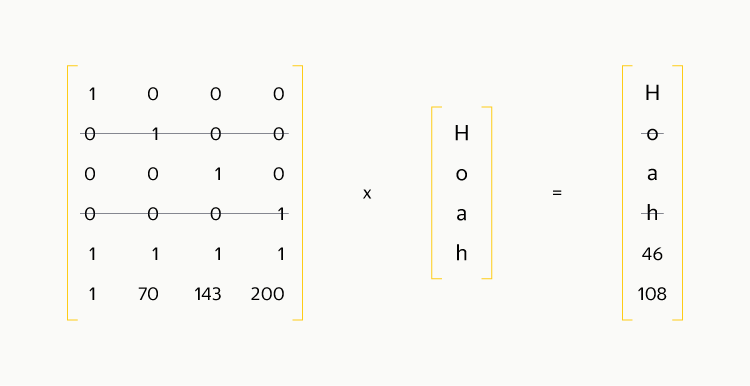
Then we reverse the resulting square matrix and multiply both sides of the equality by:

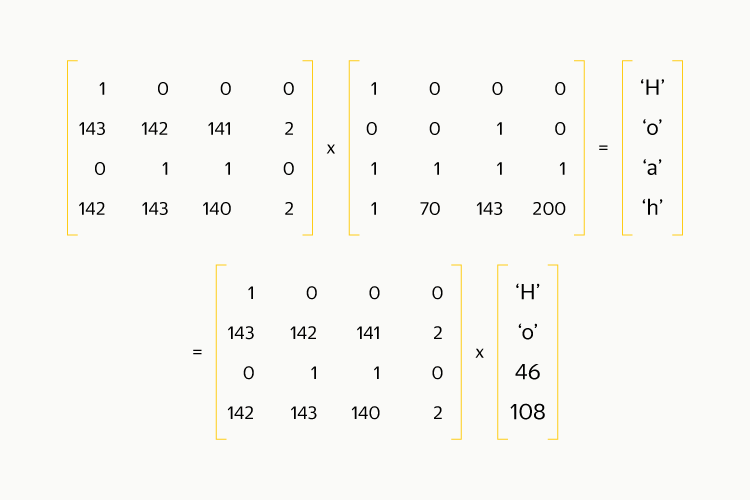
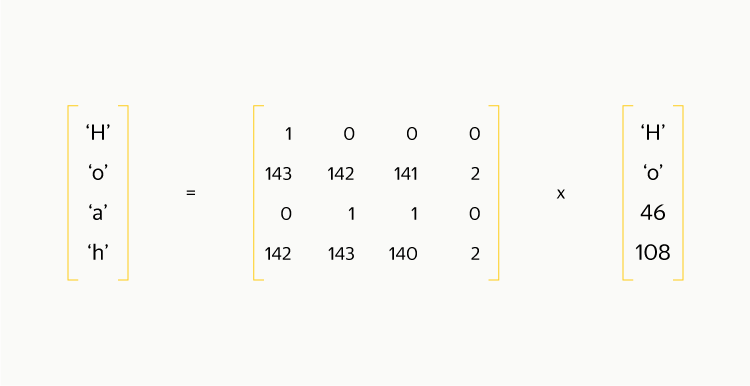
It turns out that to obtain the original data you only need to carry out the same multiplication operation as in the encoding! If only one block is lost, then from the coding matrix, in order for it to become square, you need to cross out one of the lines corresponding to the parity blocks. Note that the first line consists of ones and has a special magic: the counting is equivalent to calculating XOR between all elements and is performed several times faster than the counting of any other line. Therefore, throwing this line is not worth it.

Local Recovery Codes

It turned out quite simple and, I hope, understandable. But can anything else be improved? Yes, colleagues from Microsoft Azure tell us in their publication . This method is called the Local Reconstruction Codes (LRC). If you break all the data blocks into several groups (for example, into two groups), you can encode parity blocks in such a way as to localize error corrections within the groups. For the former replication ratio of 1.5, the scheme looks like this: we divide the stripe into two groups of four blocks, for each group there will be a local parity block plus two global parity blocks. This scheme allows you to correct any three errors and about 96% of situations with four errors. The remaining 4% are cases when all four errors fall within one group, which includes 4 data blocks and a local parity block.

Once again applying the “from simple to complex” approach, we took and divided the row of units in the coding matrix into two as follows:

one	one	one	one	0	0	0	0
0	0	0	0	one	one	one	one
one	55	39	73	84	181	225	217
one	172	70	235	143	34	200	101

Unfortunately, this time our approach failed. At first everything was fine, but when we wrote a test combinatorially sorting through all the options for theoretically recoverable errors, we found that some of them our matrix does not allow restoring. I had to dive into the study of publications. The answer was found in the same publication from Microsoft, in section 2.2.1. The matrix needs to be made a little more cunning - fortunately, jerasure allows us to do this with ease.

for row in range(4): for column in range(8): k = 8 index = row * k + column is_first_half = column < k / 2 if row == 0: matrix[index] = 1 if is_first_half else 0 elif row == 1: matrix[index] = 0 if is_first_half else 1 elif row == 2: shift = 1 if is_first_half else 2 ** (k / 2) relative_column = column if is_first_half else (column - k / 2) matrix[index] = shift * (1 + relative_column) else: prev = array[index - k] matrix[index] = libjerasure.galois_single_multiply(prev, prev, 8) 

With such a matrix, the test is successful:

one	one	one	one	0	0	0	0
0	0	0	0	one	one	one	one
one	2	3	four	sixteen	32	48	64
one	four	five	sixteen	29	116	105	205

So we formed groups. But we must not forget that the system must remain operational when the entire availability zone falls. Using LRC, this can be achieved if the blocks are arranged in zones as follows:

Here it can be seen that whatever line we cross out, there will be no more than three errors in each locality group, which means that the data can be read. If only one disk on which one block lies breaks, the data can be read by requesting only one additional block from another access zone. Considerations about the block size are about the same as in the XOR scheme, with one exception: if we assume that the reading will be too expensive only between accessibility zones, then the block size can be made four times smaller, since a continuous sequence of within one zone.

Practice

Now you understand that it is a fairly simple task to program the calculation of redundancy codes, and you can apply this knowledge in your projects. The options that we considered in the article:

• Replicas - provide multiple redundancy, are easily realizable (often - the default option), work both at the block and at the file level.
• XOR, redundancy - 1.5, can be implemented both at the block and file level, requires three availability zones.
• Reed-Solomon codes allow flexible selection of the degree of redundancy, but to restore one data block, you need to read as many blocks as one strip contains. Work well only at the block level.
• LRCs are similar to Reed-Solomon codes, but with single failures they allow reading less data, although they provide data recovery in a smaller percentage of cases.

In MDS, we applied the LRC-8-2-2 scheme (8 data blocks, 2 local parity blocks and 2 global parity blocks). As a result, 1 drop, which had 2 replicas and lived on 2 hard drives, began to be located on 12 hard drives. This significantly complicated the reading procedure, and recovery after losing the hard drive also became more difficult. But we got 25% savings in disk space, which outweighed all the disadvantages. In order to load the network less, data recording is performed in ordinary drops with replicas. We convert them only when they are completely filled and the readings become smaller - that is, when the data "cool".

We will tell about the problems that we had during the implementation of the scheme on October 15 at an event in our Moscow office. Come, it will be interesting!