Proof of Fermat's Big Theorem for a cube, as a key
<img src = "http: //  "Alt =" image "/>
"Alt =" image "/>
I consider it appropriate to submit evidence of BTF for the third degree.
Firstly: according to this method, any degree can be treated similarly.
Secondly: there is still no proof for a cube based on elementary mathematics.
And besides, due to small numerical values, when considering a cube, calculations are simplified, which makes understanding easier.
I thank in advance the possible opponents for helpful comments on the design of the evidence and, of course, for help.
And a little bile. In the perception of evidence on the Mathematical forum dxdy MSU there are no signs of understanding on the merits.
At the same time, it should be noted that part of the mathematical community that has been dealing with the problem of BTF for a considerable time, and even professionally, is concentrated there. It was on the dxdy forum that the proof was based on the consideration of the cube. I consider this requirement useful, although it did not help mutual understanding. He asked: "What is missing? What else is needed to be considered?" Silence, or, at best, recommendations to prove what has long been proven and, undoubtedly, opponents know. Currently this topic on the dxdy forum is covered: it can be read, but there is no feedback. Maybe someone on Habrhabre specifies the requirements. I want to hear the opinion.
The proof can be considered fair if it satisfies the condition:
The exponent n is a prime number. [one]
')
Consider the proof of Fermat's Great Theorem for a cube.
It is necessary to prove that

with integer
 is impossible.
is impossible.
1.1 According to the existing tradition, the proof is to consider the difference of degrees

based on the convenience of selection of grounds:

and
 .
.
1.2 At the same time, when considering any degree, two cases of the Great Fermat Theorem (BTF) are distinguished.
1.1 The first case of BTF refers to the difference of exact degrees with arbitrary bases, with the exception of the grounds providing 2 Case of BTF.
1.3 For the first case:
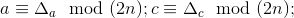

- mutually simple numbers, and the base
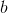 - even.
- even.
Namely, according to this variant, it is required to find a proof, and first of all for the second case of BTF.
1.4 Express the basis of equality 1.1 for the first case of the BTF through single arguments, for which we introduce the following notation:
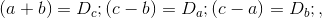
where for example

Where
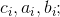 - whole numbers. [2]
- whole numbers. [2]
1.5 Therefore, equality 1.1 can be represented as:
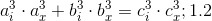
or
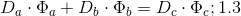
Where:

2.1. Both the first case of the BTF and the second case of the BTF are proved on the basis of the commensurability of the degrees and their bases on
 .
.
The proof is based on a comparison of the values:
 - with degree meter and
- with degree meter and
 - with base meter.
- with base meter.
2.2 When proving the first case of BTF using
 and deduction classes 1 and 5, we can express the grounds
and deduction classes 1 and 5, we can express the grounds
 :
:

Where:
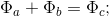
Wherein
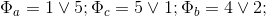
2.3 When considering the first case of BTF, when
 base
base
 may belong to the first or fifth class of deductions, and the base
may belong to the first or fifth class of deductions, and the base
 - vice versa.
- vice versa.
Because the bases belonging to the even classes of deductions are not suitable, as well as the bases belonging to the 3rd class of deductions, since in this case common factors arise in all the grounds, which contradicts the conditions of the theorem.
2.4 When considering the bases of the degrees belonging to a particular class of residues, the adjustment of the values of the bases in the Fermat equation depends only on

The characteristics of the first and second cases of the BTF affect the calculated pattern, but they do not represent any fundamental significance for the proposed evidence.
3.1 When examining the evidence for the second case of the BFT, the choice of the class of deductions for

and

It does not matter, because you can always use the transfer of any of the grounds to the first class of deductions, using a factor equal to the exact degree, based on the possibility of transferring any class of deductions that is mutually simple with the index of the degree under consideration. (Small Fermat theorem).
Therefore, when considering the second case of BTF, it is sufficient to consider the option when

3.2 For the second case of BTF, which is considered in more detail:
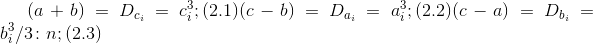
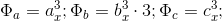
and
 where
where

- positive number of natural number series, mutually simple with value.
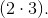
4.1 Existing pattern:
Magnitude

for exact cubes necessarily contain factors

and factor
 .
.
Therefore, we are able to consider the value
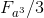 .
.
4.2 Based on the found patterns, we proceed to the analysis of the difference of degrees in order to answer the question:
When the magnitude
 may contain a factor
may contain a factor
 ?
?
4.3 To answer the question posed, we turn to the consideration of the difference in degrees, reduced to

based on the submission of grounds

and

through
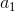
and
 and using Binom Newton. [3]
and using Binom Newton. [3]
5.1 the Ability to bring the difference in degrees to
 provided through the use of
provided through the use of
 .
.

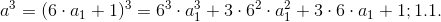 .
.
5.2 Determine the difference (1.1.-1.1.):
![(c ^ 3-a ^ 3) = 6 ^ 3 \ cdot [(c_1) ^ 3- (a_1) ^ 3] +3 \ cdot 6 ^ 2 \ cdot [(c_1) ^ 2- (a_1) ^ 2] +3 \ cdot 6 \ cdot [(c_1) - (a_1)]; 1.1](https://habrastorage.org/getpro/habr/post_images/2e9/e39/28a/2e9e3928a25f05e2b3c7ed9e0276fca6.gif) .
.
5.3 Determine
 .
.
![(c ^ 3-a ^ 3) / [3 \ cdot 6 \ cdot (c_1-a_1)] = 6 \ cdot 2 \ cdot [(c_1) ^ 2 + c_1 \ cdot (a_1) + (a_1) ^ 2] + 6 \ cdot [(c_1) + (a_1)] + 1 = b_x ^ 3; 1.1.k](https://habrastorage.org/getpro/habr/post_images/83f/241/a0a/83f241a0aa25fdfd5b3ff68b80033d6d.gif)
5.4 Determine

![F_ {b_ {x} ^ {3}} = (b_ {x} ^ {3} -1) / 6 = 2 \ cdot [(c_ {1}) ^ {2} + c_ {1} \ cdot a_ { 1} + a_ {1}) ^ {2}] + [(c_ {1}) + (a_ {1})]; 1.1.k.1](https://habrastorage.org/getpro/habr/post_images/223/2ae/eff/2232aeeff09f111afbbbf7fcc022bc79.gif)
We get the sum of two terms, the first of which contains a factor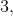 and the second is not.
and the second is not.
5.5 This is subject to the amount
![[(c_1) + (a_1)];](https://habrastorage.org/getpro/habr/post_images/e06/f46/80d/e06f4680d55a59544ff8cadd7de25e98.gif) factors
factors 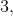 does not contain, but the difference
does not contain, but the difference

contains at least a single factor
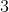 .
.
In this case, the value
 contain a factor
contain a factor
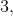 can not.
can not.
For this option, everything is clear.
5.6 To ensure an exact cube in the difference of degrees, the absence of a factor
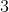
in size

we consider it a condition that cannot be overcome to refute the BTF.
6.1 To answer the question why and if there are common factors
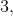 in terms of
in terms of
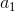 and
and

it is impossible to obtain an exact cube in the difference of cubes, we turn to the formalized expression of
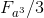
6.2 Formalized expression
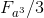 ;
;
 O.1
O.1
Example calculation A:

 ;
;
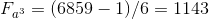 ;
;
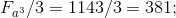
6.3 Determine
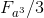
through
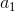

6.4 In general:
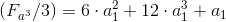 ; U.1
; U.1
6.5 Where does the exact cube come from:
 .
.
This pattern is illuminated for the possibility of miscalculation of factors.
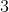
in size
 .
.
7.1 Now let us ask ourselves, at what values is provided in the value

content of factors
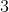 ,
,
in the amount corresponding to the filling of the same value, when considering the exact cube.
Example:
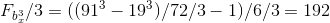 .
.
Because

it can be assumed that the basis of the proposed degree
 ,
,
minus one contains two factors
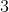 .
.
7.2 And since
 ,
,
under this assumption

contains a single factor
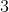 ,
,
Provides the required filling values

multipliers
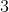 .
.
7.3 Let's try to answer the question why this result is obtained?
The selection of the grounds

and

We ensured the fulfillment of the condition:

and
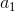
contain one common factor
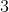 .
.
7.4 We have achieved this.
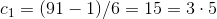
and

But analyzing the magnitude
 ,
,
notice that we have provided not a single factor
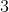 ,
,
but

This result was obtained because the sum
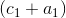
contains no scheduled additional factor
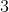 .
.
7.5 This factor, in our opinion, can be considered unrecorded.
If we draw an analogy with the infinitely small, we can see that, in contrast to the non-influence of the infinitely small on the final result, the unrecorded factor ensures the identity of the laws that exist in the assumed and true degrees, providing the uncertainty that gave rise to the problem under consideration.
In our opinion, the detection of unrecorded factors gives an explanation of the cause of the difficulty when searching for evidence of BTF.
8.1 In addition, it can be noted that the presence of an unrecorded factor in determining the difference between the bases of degrees

and

eliminates the possibility of obtaining an exact cube in the difference of degrees, and the occurrence of an unaccounted factor in the value

is a pattern that provides a predictable result.
8.2 And, in our opinion, this is an obstacle for refuting the statement of BTF, for the second case when considering the Fermat equation for the third degree and when answering the question of why and if there are common factors
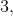
in terms of
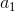
and

denial of the BTF is impossible.
8.3 We have the right to write equality:
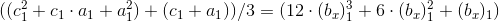 ,
,
or
 .
.
8.4 What can be written down as:
 . T
. T
8.5 Consider the condition:
 .
.
For this condition
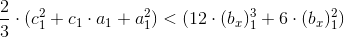
significantly
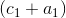 .
.
8.6 This suggests that a further increase in

does not make sense.
8.7. To show the impossibility of refuting the BTF at lower values.
 ,
,
Let us turn to the consideration of the possibility of such an event, on the example of considering the laws of magnitudes

and the same quantities corresponding to obtaining an exact cube by multiplying by
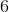
and additions
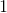 .
.
8.8 For what we consider the ratio of these values.
With
 ,
,
but

At the same time, an identical value is considered.
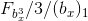
for grounds having

and
 ,
,
to confirm patterns.
8.9 If we denote the base of the cube through
 ,
,
you can build a numerical series of values
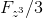 ,
,
for integer values
 :
:

and
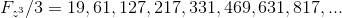 .
.
Getting calculated values
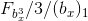 ,
,
we get the opportunity to compare them with the possible values
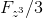 .
.
8.9.1
1. a
one.
 .
.
2
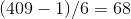 .
.
3
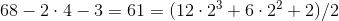 .
.
1.in
one.
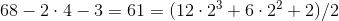 .
.
2
 .
.
3
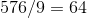 .
.
four.
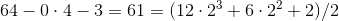 .
.
8.9.2
2. a
one
 .
.
2
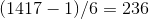
3
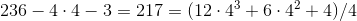
2.in
one.

2
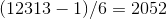
3
 .
.
four.
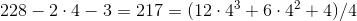 .
.
8.9.3
3. a
one
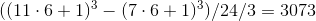 .
.
2
 .
.
3
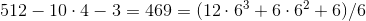 .
.
3.in
one.
 .
.
2
 .
.
3
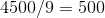 .
.
four.
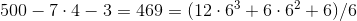 .
.
8.10
Consider the calculations of compared values for the difference of cubes, providing assumption about the possibility of refutation of the BTF.
The range between the bases is
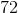 .
.
8.10.1 For
 ,
,

we get
 ,
,
Where
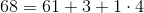
for
 ,
,
at
 .
.
Since we are interested in the difference of bases, when
 ,
,
but
 ,
,
carry out a similar calculation and with these values.
 .
.
Compare values

and
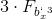 .
.
 .
.
Where:
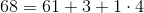 ,
,
for
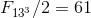 .
.
8.10.2 By analogy, for

and

 .
.
Where
 ,
,
for
 .
.
8.10.3 By analogy, for

and
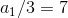
 .
.
Where
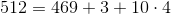 ,
,
for
 .
.
8.10.4 By analogy, for
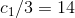
and

 .
.
Where
 ,
,
for
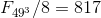 .
.
We obtain a formalized value that affects the decrease in the difference between the values we compared, but in part, as an additional increment with a minus sign.
8.11 Based on number series
 :
:
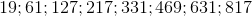 ,
,
It was established that the difference between neighboring values is always greater than the difference between the values we compared, both directly and, respectively, when they are increased three times.
8.12 On the basis of calculations, the following pattern is visible:
1. The minimum range between the obtained value
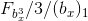
and its true meaning

increases on the basis of strict regularity, which can be formalized.
At the same time, it increases numerically, remaining minimal compared to any of the numerical series of values.
 ,
,
that is, when

and maximum when

2. Therefore, it can be argued that

is in the same dependence on the truly possible such values.
Which gives the right to assert that the refutation of BTF for the second case of BTF is not possible for a cube.
9.000 When, on the dxdy forum, someone, in my opinion, with the login Brukvalub, wrote to me:
“Do you want to do away with the Big Farm theorem?”
And why not do it that way.
The approach does not leave questions unanswered.
What else do you need?
Of course, of course, a clear statement and recognition.
Someone wrote on Habrahabr that the proof becomes proof only after its recognition.
It does not become, but is considered.
And it becomes a proof after there are no tricky questions left.
Such questions are not known to me at the moment.
True, with silent opponents.
In the presence of the interlocutor, and better co-author, you can consider something, and additionally. And a detailed look at what follows.
And one more thing: it turned out to be harder than to prove.
9.1 Let us proceed to consider the features of the first case of BTF for a cube.
To this end, we consider another found pattern.
In determining
 rightly so:
rightly so:
![F_ {b_x ^ n} = (b_x ^ n-1) / (2n) = [(c ^ na ^ n) / [n (ca)] - 1] / (2n) $$ = [[(c ^ n -1) / (2 \ cdot n) - (a ^ n-1) / (2 \ cdot n)] / [n \ cdot (c_1-a_1)] -1] / (2 \ cdot 3); F_ {b_x ^ n} = (b_x ^ n-1) / (2n) = \ frac {[(c ^ na ^ n) / (ca) -1]} {2n} = \ frac {[(c ^ n \ pm \ Delta_c) / (2n) - (a ^ n \ pm \ Delta_a)] / (2n) - (c_1-a_1)} {ca};](https://habrastorage.org/getpro/habr/post_images/da0/826/0d1/da08260d182e2fd35ade19371cd46c0b.gif)
9.2 Ah, exactly.
![F_ {b_x ^ n} = (b_x ^ n-1) / (2n) = \ frac {[(c ^ na ^ n) / (ca) -1]} {2n} = \ frac {[(c ^ n \ pm \ Delta_c) / (2n) - (a ^ n \ pm \ Delta_a)] / (2n) - (c_1-a_1)} {ca} and](https://habrastorage.org/getpro/habr/post_images/790/a27/cdb/790a27cdb8b9f53f6ff59166405de8f6.gif) .
.
The need for adjustment

due to the difference in the number of quantities
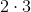 accepted for calculation.
accepted for calculation.
9.3 This allows us to equate the consideration of the second and first cases, since finding the difference of degrees for the first case of BTF leads to a similar variant, identical to the second case of BTF.
Therefore, it can be noted that the statement of the Great Fermat theorem holds true for both the second case and the first case when considering a cube.
Q.E.D.
PS The proof for an arbitrary degree differs from the proof for a cube by the peculiarities of the calculation both in numerical and, of course, in a formalized form.
In this case, the formalization of the value
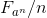
based on similar pitches used when considering a cube.
The occurrence of unrecorded factors when considering BTF with increasing degree considered has a similar explanation explaining the occurrence of such factors when considering a cube.
In addition to the above, it should be noted that the proof of the BTF for arbitrary exponents of degrees is also seen through the use of the developments found in the consideration of the cube.
Of course, everything not considered specifically requires specific consideration, but, alone, the author is not uplifting.
Unfortunately, the desired is not provided at Habrahabr.
But, the hope is that it may be useful to someone.
The author does not doubt the truth of the proof, and is satisfied with it.
And, especially, the fact that the proof became possible through the use of patterns, the so-called elementary mathematics, which allow, in spite of its elementary nature, to get to the point that it is not always possible for her venerable fellows.
It remains evidence to cut and polish.
And here, would not prevent advice.
However, if there are protesters, or abstentions, you are welcome to speak.
Literature:
1. G. Edwards "Fermat's last theorem".
2. MM Postnikov, "Introduction to the theory of algebraic numbers."
3. M.YA. Vygodsky "Handbook of elementary mathematics."
 "Alt =" image "/>
"Alt =" image "/>I consider it appropriate to submit evidence of BTF for the third degree.
Firstly: according to this method, any degree can be treated similarly.
Secondly: there is still no proof for a cube based on elementary mathematics.
And besides, due to small numerical values, when considering a cube, calculations are simplified, which makes understanding easier.
I thank in advance the possible opponents for helpful comments on the design of the evidence and, of course, for help.
And a little bile. In the perception of evidence on the Mathematical forum dxdy MSU there are no signs of understanding on the merits.
At the same time, it should be noted that part of the mathematical community that has been dealing with the problem of BTF for a considerable time, and even professionally, is concentrated there. It was on the dxdy forum that the proof was based on the consideration of the cube. I consider this requirement useful, although it did not help mutual understanding. He asked: "What is missing? What else is needed to be considered?" Silence, or, at best, recommendations to prove what has long been proven and, undoubtedly, opponents know. Currently this topic on the dxdy forum is covered: it can be read, but there is no feedback. Maybe someone on Habrhabre specifies the requirements. I want to hear the opinion.
The proof can be considered fair if it satisfies the condition:
The exponent n is a prime number. [one]
')
Consider the proof of Fermat's Great Theorem for a cube.
It is necessary to prove that

with integer
 is impossible.
is impossible.Introduction
1.1 According to the existing tradition, the proof is to consider the difference of degrees

based on the convenience of selection of grounds:

and
 .
.1.2 At the same time, when considering any degree, two cases of the Great Fermat Theorem (BTF) are distinguished.
1.1 The first case of BTF refers to the difference of exact degrees with arbitrary bases, with the exception of the grounds providing 2 Case of BTF.
1.3 For the first case:
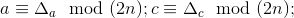

- mutually simple numbers, and the base
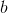 - even.
- even. Namely, according to this variant, it is required to find a proof, and first of all for the second case of BTF.
1.4 Express the basis of equality 1.1 for the first case of the BTF through single arguments, for which we introduce the following notation:
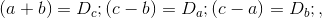
where for example

Where
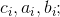 - whole numbers. [2]
- whole numbers. [2] 1.5 Therefore, equality 1.1 can be represented as:
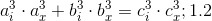
or
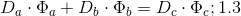
Where:

2.1. Both the first case of the BTF and the second case of the BTF are proved on the basis of the commensurability of the degrees and their bases on
 .
. The proof is based on a comparison of the values:
 - with degree meter and
- with degree meter and  - with base meter.
- with base meter. 2.2 When proving the first case of BTF using
 and deduction classes 1 and 5, we can express the grounds
and deduction classes 1 and 5, we can express the grounds  :
: 
Where:
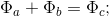
Wherein
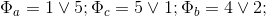
2.3 When considering the first case of BTF, when
 base
base  may belong to the first or fifth class of deductions, and the base
may belong to the first or fifth class of deductions, and the base  - vice versa.
- vice versa. Because the bases belonging to the even classes of deductions are not suitable, as well as the bases belonging to the 3rd class of deductions, since in this case common factors arise in all the grounds, which contradicts the conditions of the theorem.
2.4 When considering the bases of the degrees belonging to a particular class of residues, the adjustment of the values of the bases in the Fermat equation depends only on

The characteristics of the first and second cases of the BTF affect the calculated pattern, but they do not represent any fundamental significance for the proposed evidence.
3.1 When examining the evidence for the second case of the BFT, the choice of the class of deductions for

and

It does not matter, because you can always use the transfer of any of the grounds to the first class of deductions, using a factor equal to the exact degree, based on the possibility of transferring any class of deductions that is mutually simple with the index of the degree under consideration. (Small Fermat theorem).
Therefore, when considering the second case of BTF, it is sufficient to consider the option when

3.2 For the second case of BTF, which is considered in more detail:
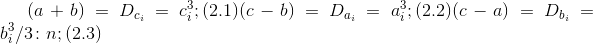
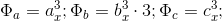
and
 where
where 
- positive number of natural number series, mutually simple with value.
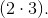
Proof of the second case of BTF.
4.1 Existing pattern:
Magnitude

for exact cubes necessarily contain factors

and factor
 .
.Therefore, we are able to consider the value
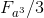 .
.4.2 Based on the found patterns, we proceed to the analysis of the difference of degrees in order to answer the question:
When the magnitude
 may contain a factor
may contain a factor ?
?4.3 To answer the question posed, we turn to the consideration of the difference in degrees, reduced to

based on the submission of grounds

and

through
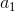
and
 and using Binom Newton. [3]
and using Binom Newton. [3]5.1 the Ability to bring the difference in degrees to
 provided through the use of
provided through the use of .
.
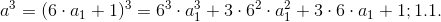 .
.5.2 Determine the difference (1.1.-1.1.):
![(c ^ 3-a ^ 3) = 6 ^ 3 \ cdot [(c_1) ^ 3- (a_1) ^ 3] +3 \ cdot 6 ^ 2 \ cdot [(c_1) ^ 2- (a_1) ^ 2] +3 \ cdot 6 \ cdot [(c_1) - (a_1)]; 1.1](https://habrastorage.org/getpro/habr/post_images/2e9/e39/28a/2e9e3928a25f05e2b3c7ed9e0276fca6.gif) .
.5.3 Determine
 .
.![(c ^ 3-a ^ 3) / [3 \ cdot 6 \ cdot (c_1-a_1)] = 6 \ cdot 2 \ cdot [(c_1) ^ 2 + c_1 \ cdot (a_1) + (a_1) ^ 2] + 6 \ cdot [(c_1) + (a_1)] + 1 = b_x ^ 3; 1.1.k](https://habrastorage.org/getpro/habr/post_images/83f/241/a0a/83f241a0aa25fdfd5b3ff68b80033d6d.gif)
5.4 Determine

![F_ {b_ {x} ^ {3}} = (b_ {x} ^ {3} -1) / 6 = 2 \ cdot [(c_ {1}) ^ {2} + c_ {1} \ cdot a_ { 1} + a_ {1}) ^ {2}] + [(c_ {1}) + (a_ {1})]; 1.1.k.1](https://habrastorage.org/getpro/habr/post_images/223/2ae/eff/2232aeeff09f111afbbbf7fcc022bc79.gif)
We get the sum of two terms, the first of which contains a factor
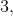 and the second is not.
and the second is not.5.5 This is subject to the amount
![[(c_1) + (a_1)];](https://habrastorage.org/getpro/habr/post_images/e06/f46/80d/e06f4680d55a59544ff8cadd7de25e98.gif) factors
factors 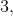 does not contain, but the difference
does not contain, but the difference
contains at least a single factor
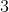 .
.In this case, the value
 contain a factor
contain a factor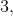 can not.
can not.For this option, everything is clear.
5.6 To ensure an exact cube in the difference of degrees, the absence of a factor
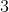
in size

we consider it a condition that cannot be overcome to refute the BTF.
6.1 To answer the question why and if there are common factors
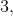 in terms of
in terms of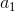 and
and
it is impossible to obtain an exact cube in the difference of cubes, we turn to the formalized expression of
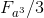
6.2 Formalized expression
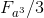 ;
; O.1
O.1Example calculation A:

 ;
;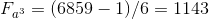 ;
;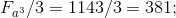
6.3 Determine
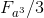
through
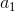

6.4 In general:
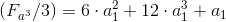 ; U.1
; U.16.5 Where does the exact cube come from:
 .
.This pattern is illuminated for the possibility of miscalculation of factors.
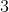
in size
 .
.7.1 Now let us ask ourselves, at what values is provided in the value

content of factors
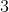 ,
,in the amount corresponding to the filling of the same value, when considering the exact cube.
Example:
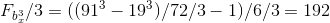 .
.Because

it can be assumed that the basis of the proposed degree
 ,
,minus one contains two factors
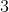 .
.7.2 And since
 ,
,under this assumption

contains a single factor
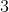 ,
,Provides the required filling values

multipliers
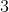 .
.7.3 Let's try to answer the question why this result is obtained?
The selection of the grounds

and

We ensured the fulfillment of the condition:

and
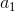
contain one common factor
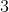 .
.7.4 We have achieved this.
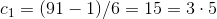
and

But analyzing the magnitude
 ,
,notice that we have provided not a single factor
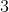 ,
,but

This result was obtained because the sum
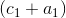
contains no scheduled additional factor
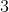 .
.7.5 This factor, in our opinion, can be considered unrecorded.
If we draw an analogy with the infinitely small, we can see that, in contrast to the non-influence of the infinitely small on the final result, the unrecorded factor ensures the identity of the laws that exist in the assumed and true degrees, providing the uncertainty that gave rise to the problem under consideration.
In our opinion, the detection of unrecorded factors gives an explanation of the cause of the difficulty when searching for evidence of BTF.
8.1 In addition, it can be noted that the presence of an unrecorded factor in determining the difference between the bases of degrees

and

eliminates the possibility of obtaining an exact cube in the difference of degrees, and the occurrence of an unaccounted factor in the value

is a pattern that provides a predictable result.
8.2 And, in our opinion, this is an obstacle for refuting the statement of BTF, for the second case when considering the Fermat equation for the third degree and when answering the question of why and if there are common factors
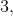
in terms of
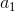
and

denial of the BTF is impossible.
8.3 We have the right to write equality:
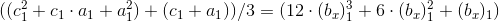 ,
,or
 .
.8.4 What can be written down as:
 . T
. T8.5 Consider the condition:
 .
.For this condition
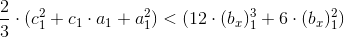
significantly
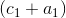 .
.8.6 This suggests that a further increase in

does not make sense.
8.7. To show the impossibility of refuting the BTF at lower values.
 ,
,Let us turn to the consideration of the possibility of such an event, on the example of considering the laws of magnitudes

and the same quantities corresponding to obtaining an exact cube by multiplying by
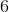
and additions
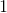 .
.8.8 For what we consider the ratio of these values.
With
 ,
,but

At the same time, an identical value is considered.
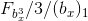
for grounds having

and
 ,
,to confirm patterns.
8.9 If we denote the base of the cube through
 ,
,you can build a numerical series of values
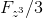 ,
,for integer values
 :
:
and
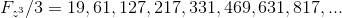 .
.Getting calculated values
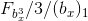 ,
,we get the opportunity to compare them with the possible values
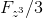 .
.8.9.1
1. a
one.
 .
.2
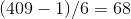 .
.3
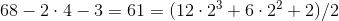 .
.1.in
one.
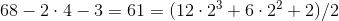 .
.2
 .
.3
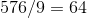 .
.four.
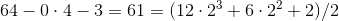 .
.8.9.2
2. a
one
 .
.2
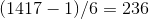
3
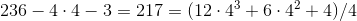
2.in
one.

2
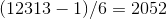
3
 .
.four.
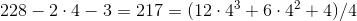 .
.8.9.3
3. a
one
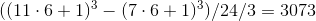 .
.2
 .
.3
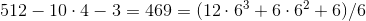 .
.3.in
one.
 .
.2
 .
.3
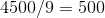 .
.four.
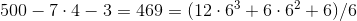 .
.8.10
Consider the calculations of compared values for the difference of cubes, providing assumption about the possibility of refutation of the BTF.
The range between the bases is
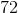 .
.8.10.1 For
 ,
,
we get
 ,
,Where
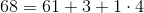
for
 ,
,at
 .
.Since we are interested in the difference of bases, when
 ,
,but
 ,
,carry out a similar calculation and with these values.
 .
.Compare values

and
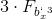 .
. .
.Where:
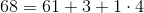 ,
,for
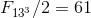 .
.8.10.2 By analogy, for

and

 .
.Where
 ,
,for
 .
.8.10.3 By analogy, for

and
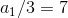
 .
.Where
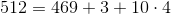 ,
,for
 .
.8.10.4 By analogy, for
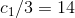
and

 .
.Where
 ,
,for
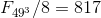 .
.We obtain a formalized value that affects the decrease in the difference between the values we compared, but in part, as an additional increment with a minus sign.
8.11 Based on number series
 :
: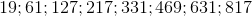 ,
,It was established that the difference between neighboring values is always greater than the difference between the values we compared, both directly and, respectively, when they are increased three times.
8.12 On the basis of calculations, the following pattern is visible:
1. The minimum range between the obtained value
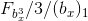
and its true meaning

increases on the basis of strict regularity, which can be formalized.
At the same time, it increases numerically, remaining minimal compared to any of the numerical series of values.
 ,
,that is, when

and maximum when

2. Therefore, it can be argued that

is in the same dependence on the truly possible such values.
Which gives the right to assert that the refutation of BTF for the second case of BTF is not possible for a cube.
9.000 When, on the dxdy forum, someone, in my opinion, with the login Brukvalub, wrote to me:
“Do you want to do away with the Big Farm theorem?”
And why not do it that way.
The approach does not leave questions unanswered.
What else do you need?
Of course, of course, a clear statement and recognition.
Someone wrote on Habrahabr that the proof becomes proof only after its recognition.
It does not become, but is considered.
And it becomes a proof after there are no tricky questions left.
Such questions are not known to me at the moment.
True, with silent opponents.
In the presence of the interlocutor, and better co-author, you can consider something, and additionally. And a detailed look at what follows.
And one more thing: it turned out to be harder than to prove.
9.1 Let us proceed to consider the features of the first case of BTF for a cube.
To this end, we consider another found pattern.
In determining
 rightly so:
rightly so:![F_ {b_x ^ n} = (b_x ^ n-1) / (2n) = [(c ^ na ^ n) / [n (ca)] - 1] / (2n) $$ = [[(c ^ n -1) / (2 \ cdot n) - (a ^ n-1) / (2 \ cdot n)] / [n \ cdot (c_1-a_1)] -1] / (2 \ cdot 3); F_ {b_x ^ n} = (b_x ^ n-1) / (2n) = \ frac {[(c ^ na ^ n) / (ca) -1]} {2n} = \ frac {[(c ^ n \ pm \ Delta_c) / (2n) - (a ^ n \ pm \ Delta_a)] / (2n) - (c_1-a_1)} {ca};](https://habrastorage.org/getpro/habr/post_images/da0/826/0d1/da08260d182e2fd35ade19371cd46c0b.gif)
9.2 Ah, exactly.
![F_ {b_x ^ n} = (b_x ^ n-1) / (2n) = \ frac {[(c ^ na ^ n) / (ca) -1]} {2n} = \ frac {[(c ^ n \ pm \ Delta_c) / (2n) - (a ^ n \ pm \ Delta_a)] / (2n) - (c_1-a_1)} {ca} and](https://habrastorage.org/getpro/habr/post_images/790/a27/cdb/790a27cdb8b9f53f6ff59166405de8f6.gif) .
.The need for adjustment

due to the difference in the number of quantities
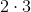 accepted for calculation.
accepted for calculation.9.3 This allows us to equate the consideration of the second and first cases, since finding the difference of degrees for the first case of BTF leads to a similar variant, identical to the second case of BTF.
Therefore, it can be noted that the statement of the Great Fermat theorem holds true for both the second case and the first case when considering a cube.
Q.E.D.
PS The proof for an arbitrary degree differs from the proof for a cube by the peculiarities of the calculation both in numerical and, of course, in a formalized form.
In this case, the formalization of the value
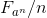
based on similar pitches used when considering a cube.
The occurrence of unrecorded factors when considering BTF with increasing degree considered has a similar explanation explaining the occurrence of such factors when considering a cube.
In addition to the above, it should be noted that the proof of the BTF for arbitrary exponents of degrees is also seen through the use of the developments found in the consideration of the cube.
Of course, everything not considered specifically requires specific consideration, but, alone, the author is not uplifting.
Unfortunately, the desired is not provided at Habrahabr.
But, the hope is that it may be useful to someone.
The author does not doubt the truth of the proof, and is satisfied with it.
And, especially, the fact that the proof became possible through the use of patterns, the so-called elementary mathematics, which allow, in spite of its elementary nature, to get to the point that it is not always possible for her venerable fellows.
It remains evidence to cut and polish.
And here, would not prevent advice.
However, if there are protesters, or abstentions, you are welcome to speak.
Literature:
1. G. Edwards "Fermat's last theorem".
2. MM Postnikov, "Introduction to the theory of algebraic numbers."
3. M.YA. Vygodsky "Handbook of elementary mathematics."
Source: https://habr.com/ru/post/311728/
All Articles