About degrees of freedom in statistics
In one of the previous posts, we discussed, perhaps, the central concept in data analysis and hypothesis testing - the p-level of significance. If we do not use the Bayesian approach, then we use exactly the p-value to decide whether we have enough reason to reject the null hypothesis of our study, i.e. proud to tell the world that we have obtained statistically significant differences.
However, in most statistical tests used to test hypotheses (for example, t-test, regression analysis, analysis of variance), there is always an indicator next to the p-value such as the number of degrees of freedom, it is degrees of freedom or simply abbreviated df, about it We will talk today.

In my opinion, the concept of degrees of freedom in statistics is remarkable in that it is also one of the most important in applied statistics (we need to know df to calculate the p-value in the voiced tests), but at the same time one of the most difficult to understand definitions for non-mathematicians studying statistics.
')
Let's look at an example of a small statistical study to understand why we need the df indicator, and what is the problem with it. Suppose we decided to test the hypothesis that the average height of St. Petersburg residents is 170 centimeters. For these purposes, we scored a sample of 16 people and obtained the following results: the average growth in the sample was 173 with a standard deviation equal to 4. To test our hypothesis, one-sample Student's t-test can be used, allowing us to estimate how strongly the sample average deviated from the expected average in the total population in units of standard error:
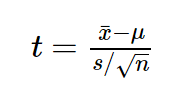
We will carry out the necessary calculations and get that the value of the t-test is 3, great, it remains to calculate the p-value and the problem is solved. However, having familiarized with the features of the t-distribution, we find out that its shape differs depending on the number of degrees of freedom calculated using the formula n-1, where n is the number of observations in the sample:
By itself, the formula for calculating df looks very friendly, substituted the number of observations, subtracted one and the answer is ready: it remains to calculate the value of p-value, which in our case is equal to 0.004.
When for the first time in my life at a lecture on statistics I ran into this procedure, I, like many students, had a legitimate question: why do we subtract a unit? Why do not we deduct a deuce, for example? And why do we even need to subtract something from the number of observations in our sample?
In the textbook, I read the following explanation, which I met several times in the future as an answer to this question:
“Suppose we know what the sample mean equals, then we only need to know the n-1 elements of the sample in order to accurately determine what the remaining n element is.” It sounds reasonable, but this explanation describes some mathematical technique rather than explains why we needed to use it when calculating the t-test. The following common explanation is as follows: the number of degrees of freedom is the difference between the number of observations and the number of parameters estimated. When using a single-sample t-test, we estimated one parameter — the average value in the general population, using n elements of the sample, which means df = n-1.
However, neither the first nor the second explanation helps to understand why we needed to subtract the number of estimated parameters from the number of observations?
Let's move a little further in search of an answer. First we turn to the definition of the t-distribution, it is obvious that all the answers are hidden in it. So a random variable:
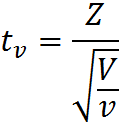
has a t-distribution with df = ν, provided that Z is a random variable with the standard normal distribution N (0; 1), V is a random variable with the chi-square distribution, with ν number of degrees of freedom, the random variables Z and V are independent . This is already a serious step forward; it turns out that a random variable with the Chi-square distribution in the denominator of our formula is responsible for the number of degrees of freedom.
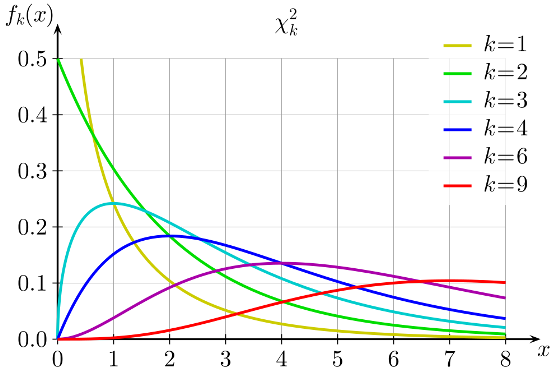
Let us then study the definition of the chi-squared distribution. The chi-square distribution with k degrees of freedom is the distribution of the sum of squares of k independent standard normal random variables.
It seems that we are already quite at the goal, at least now we know for sure that such a number of degrees of freedom of a chi-square distribution is simply the number of independent random variables with a normal standard distribution that we summarize. But it is still unclear at what stage and why did we need to subtract a unit from this value?
Let's look at a small example that clearly illustrates this need. Suppose we love to make important life decisions based on the result of a coin flip. However, lately, we suspected our coin that she too often falls eagle. To try to reject the hypothesis that our coin is actually fair, we recorded the results of 100 shots and got the following result: an eagle fell 60 times and only 40 times fell tails. Do we have enough reason to reject the hypothesis that the coin is fair? The Pearson Chi-square distribution will help us with this. After all, if the coin were truly honest, then the expected, theoretical frequencies of falling of the eagle and tails would be the same, that is, 50 and 50. It is easy to calculate how strongly the observed frequencies deviate from the expected ones. To do this, we calculate the Pearson Chi-square distance according to, I think, the formula familiar to most readers:
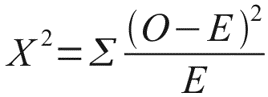
Where O is the observed, E is the expected frequency.
The fact is that if the null hypothesis is true, then with repeated repetition of our experiment, the distribution of the difference between the observed and expected frequencies divided by the root of the observed frequency can be described using the normal standard distribution, and the sum of squares k of such random normal values will be By definition, a random variable with a chi-square distribution.
Let's illustrate this thesis graphically, let's say we have two random, independent values that have a standard normal distribution. Then their joint distribution will look like this:
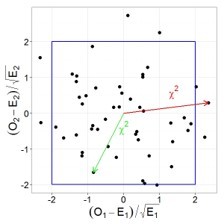
In this case, the square of the distance from zero to each point will be a random variable having a chi-square distribution with two degrees of freedom. Recalling the Pythagorean theorem, it is easy to verify that this distance is the sum of the squares of the values of both quantities.
Well, now the culmination of our story. We return to our formula for calculating the Chi-square distance to check the integrity of the coin, substitute the available data into the formula, and we find that the Pearson Chi-square distance is 4. However, to determine the p-value we need to know the number of degrees of freedom, because the Chi-square distribution form depends on this parameter, respectively, and the critical value will also vary depending on this parameter.
Now the fun part. Suppose we decided to repeat 100 shots many times, and each time we recorded the observed frequencies of the eagles and tails, we calculated the required indicators (the difference between the observed and expected frequencies divided by the root of the expected frequency) and, as in the previous example, plotted them.
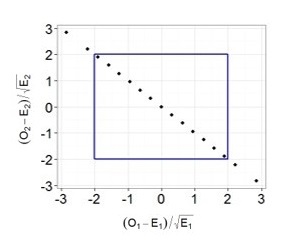
It is easy to notice that now all points are lined up in one line. The thing is that in the case of a coin, our terms are not independent, knowing the total number of throws and the number of tails, we can always accurately determine the number of eagles that fell out and vice versa, so we cannot say that our two terms are two independent random magnitude. You can also make sure that all the points will always always lie on one straight line: if we had 30 eagles, it means we had 70, if we had 70, then we would have 30, etc. Thus, despite the fact that there were two terms in our formula, we will use the Chi-square distribution with one degree of freedom to calculate the p-value! So we finally got to the point where we needed to subtract a unit. If we were to test the hypothesis that our six-sided dice is fair, then we would use a chi-squared distribution with 5 degrees of freedom. After all, knowing the total number of shots and the observed drop rates of any five faces, we can always determine exactly what the number of sixth face drops.
Now, armed with this knowledge, let's return to the t-test:
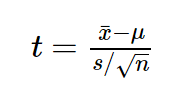
in the denominator we have the standard error, which is a sample standard deviation divided by the root of the sample size. The calculation of the standard deviation includes the sum of the squares of the deviations of the observed values from their average value — that is, the sum of several random positive values. And we already know that the sum of squares of n random variables can be described using the chi-squared distribution. However, despite the fact that we have n terms, this distribution will have n-1 degrees of freedom, since knowing the sample mean and n-1 elements of the sample, we can always accurately specify the last element (this is where the explanation about the average and n-1 elements needed to uniquely determine the n element)! It turns out that in the denominator of t-statistics we have hidden the chi-square distribution with n-1 degrees of freedom, which is used to describe the distribution of the sample standard deviation! Thus, the degrees of freedom in the t-distribution are actually taken from the chi-square distribution, which is hidden in the t-statistic formula. Incidentally, it is important to note that all of the above reasoning is valid if the subject studied has a normal distribution in the general population (or the sample size is large enough), and if we really had a goal to test the hypothesis of the average value of growth in a population, it would probably be it is wiser to use a non-parametric test.
A similar logic for calculating the number of degrees of freedom is preserved when working with other tests, for example, in regression or analysis of variance, it is all a matter of random variables with the Chi-square distribution that are present in the formulas for calculating the corresponding criteria.
Thus, in order to correctly interpret the results of statistical studies and understand where all the indicators come from, which we get when using even such a simple criterion as a one-sample t-test, any researcher needs to understand well what mathematical ideas lie at the basis of statistical methods.
Based on the experience of teaching statistics at the Institute of Bioinformatics , we had the idea to create a series of online courses on data analysis, in which the most important topics will be explained in accessible form for each, understanding of which is necessary for confident use of statistics methods in solving various types of problems. In 2015, we launched the Fundamentals of Statistics course, to which about 17 thousand people have registered today, three thousand students have already received a certificate of its successful completion, and the course itself was awarded the EdCrunch Awards and was recognized as the best technical course. This year, the continuation of the Fundamentals of Statistics course was launched on the stepik.org platform . Part two , in which we continue to get acquainted with the basic methods of statistics and analyze the most complex theoretical issues. By the way, one of the main topics of the course is the role of the Pearson Chi-square distribution when testing statistical hypotheses. So if you still have questions about why we subtract a unit from the total number of observations, we are waiting for you on the course!
It is also worth noting that theoretical knowledge in the field of statistics will definitely be useful not only to those who use statistics for academic purposes, but also to those who use data analysis in applied fields. Basic knowledge in the field of statistics is simply necessary for mastering more complex methods and approaches used in the field of machine learning and Data Mining. Thus, the successful completion of our courses on introducing statistics is a good start in the field of data analysis. Well, if you are seriously thinking about acquiring data skills, we think you might be interested in our online data analysis program, which we wrote about in more detail here . These statistics courses are part of this program and will allow you to seamlessly plunge into the world of statistics and machine learning. However, those who wish can take these courses without deadlines outside the context of the data analysis program.
However, in most statistical tests used to test hypotheses (for example, t-test, regression analysis, analysis of variance), there is always an indicator next to the p-value such as the number of degrees of freedom, it is degrees of freedom or simply abbreviated df, about it We will talk today.

Degree of freedom, what are you talking about?
In my opinion, the concept of degrees of freedom in statistics is remarkable in that it is also one of the most important in applied statistics (we need to know df to calculate the p-value in the voiced tests), but at the same time one of the most difficult to understand definitions for non-mathematicians studying statistics.
')
Let's look at an example of a small statistical study to understand why we need the df indicator, and what is the problem with it. Suppose we decided to test the hypothesis that the average height of St. Petersburg residents is 170 centimeters. For these purposes, we scored a sample of 16 people and obtained the following results: the average growth in the sample was 173 with a standard deviation equal to 4. To test our hypothesis, one-sample Student's t-test can be used, allowing us to estimate how strongly the sample average deviated from the expected average in the total population in units of standard error:
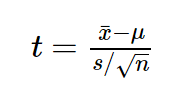
We will carry out the necessary calculations and get that the value of the t-test is 3, great, it remains to calculate the p-value and the problem is solved. However, having familiarized with the features of the t-distribution, we find out that its shape differs depending on the number of degrees of freedom calculated using the formula n-1, where n is the number of observations in the sample:

By itself, the formula for calculating df looks very friendly, substituted the number of observations, subtracted one and the answer is ready: it remains to calculate the value of p-value, which in our case is equal to 0.004.
But why n minus one?
When for the first time in my life at a lecture on statistics I ran into this procedure, I, like many students, had a legitimate question: why do we subtract a unit? Why do not we deduct a deuce, for example? And why do we even need to subtract something from the number of observations in our sample?
In the textbook, I read the following explanation, which I met several times in the future as an answer to this question:
“Suppose we know what the sample mean equals, then we only need to know the n-1 elements of the sample in order to accurately determine what the remaining n element is.” It sounds reasonable, but this explanation describes some mathematical technique rather than explains why we needed to use it when calculating the t-test. The following common explanation is as follows: the number of degrees of freedom is the difference between the number of observations and the number of parameters estimated. When using a single-sample t-test, we estimated one parameter — the average value in the general population, using n elements of the sample, which means df = n-1.
However, neither the first nor the second explanation helps to understand why we needed to subtract the number of estimated parameters from the number of observations?
And here is the Pearson Chi-square distribution?
Let's move a little further in search of an answer. First we turn to the definition of the t-distribution, it is obvious that all the answers are hidden in it. So a random variable:
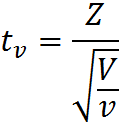
has a t-distribution with df = ν, provided that Z is a random variable with the standard normal distribution N (0; 1), V is a random variable with the chi-square distribution, with ν number of degrees of freedom, the random variables Z and V are independent . This is already a serious step forward; it turns out that a random variable with the Chi-square distribution in the denominator of our formula is responsible for the number of degrees of freedom.
Let us then study the definition of the chi-squared distribution. The chi-square distribution with k degrees of freedom is the distribution of the sum of squares of k independent standard normal random variables.
It seems that we are already quite at the goal, at least now we know for sure that such a number of degrees of freedom of a chi-square distribution is simply the number of independent random variables with a normal standard distribution that we summarize. But it is still unclear at what stage and why did we need to subtract a unit from this value?
Let's look at a small example that clearly illustrates this need. Suppose we love to make important life decisions based on the result of a coin flip. However, lately, we suspected our coin that she too often falls eagle. To try to reject the hypothesis that our coin is actually fair, we recorded the results of 100 shots and got the following result: an eagle fell 60 times and only 40 times fell tails. Do we have enough reason to reject the hypothesis that the coin is fair? The Pearson Chi-square distribution will help us with this. After all, if the coin were truly honest, then the expected, theoretical frequencies of falling of the eagle and tails would be the same, that is, 50 and 50. It is easy to calculate how strongly the observed frequencies deviate from the expected ones. To do this, we calculate the Pearson Chi-square distance according to, I think, the formula familiar to most readers:
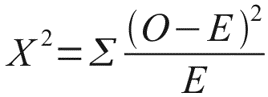
Where O is the observed, E is the expected frequency.
The fact is that if the null hypothesis is true, then with repeated repetition of our experiment, the distribution of the difference between the observed and expected frequencies divided by the root of the observed frequency can be described using the normal standard distribution, and the sum of squares k of such random normal values will be By definition, a random variable with a chi-square distribution.
Let's illustrate this thesis graphically, let's say we have two random, independent values that have a standard normal distribution. Then their joint distribution will look like this:

In this case, the square of the distance from zero to each point will be a random variable having a chi-square distribution with two degrees of freedom. Recalling the Pythagorean theorem, it is easy to verify that this distance is the sum of the squares of the values of both quantities.
It's time to subtract one!
Well, now the culmination of our story. We return to our formula for calculating the Chi-square distance to check the integrity of the coin, substitute the available data into the formula, and we find that the Pearson Chi-square distance is 4. However, to determine the p-value we need to know the number of degrees of freedom, because the Chi-square distribution form depends on this parameter, respectively, and the critical value will also vary depending on this parameter.

Now the fun part. Suppose we decided to repeat 100 shots many times, and each time we recorded the observed frequencies of the eagles and tails, we calculated the required indicators (the difference between the observed and expected frequencies divided by the root of the expected frequency) and, as in the previous example, plotted them.

It is easy to notice that now all points are lined up in one line. The thing is that in the case of a coin, our terms are not independent, knowing the total number of throws and the number of tails, we can always accurately determine the number of eagles that fell out and vice versa, so we cannot say that our two terms are two independent random magnitude. You can also make sure that all the points will always always lie on one straight line: if we had 30 eagles, it means we had 70, if we had 70, then we would have 30, etc. Thus, despite the fact that there were two terms in our formula, we will use the Chi-square distribution with one degree of freedom to calculate the p-value! So we finally got to the point where we needed to subtract a unit. If we were to test the hypothesis that our six-sided dice is fair, then we would use a chi-squared distribution with 5 degrees of freedom. After all, knowing the total number of shots and the observed drop rates of any five faces, we can always determine exactly what the number of sixth face drops.
Everything falls into place
Now, armed with this knowledge, let's return to the t-test:
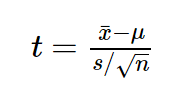
in the denominator we have the standard error, which is a sample standard deviation divided by the root of the sample size. The calculation of the standard deviation includes the sum of the squares of the deviations of the observed values from their average value — that is, the sum of several random positive values. And we already know that the sum of squares of n random variables can be described using the chi-squared distribution. However, despite the fact that we have n terms, this distribution will have n-1 degrees of freedom, since knowing the sample mean and n-1 elements of the sample, we can always accurately specify the last element (this is where the explanation about the average and n-1 elements needed to uniquely determine the n element)! It turns out that in the denominator of t-statistics we have hidden the chi-square distribution with n-1 degrees of freedom, which is used to describe the distribution of the sample standard deviation! Thus, the degrees of freedom in the t-distribution are actually taken from the chi-square distribution, which is hidden in the t-statistic formula. Incidentally, it is important to note that all of the above reasoning is valid if the subject studied has a normal distribution in the general population (or the sample size is large enough), and if we really had a goal to test the hypothesis of the average value of growth in a population, it would probably be it is wiser to use a non-parametric test.
A similar logic for calculating the number of degrees of freedom is preserved when working with other tests, for example, in regression or analysis of variance, it is all a matter of random variables with the Chi-square distribution that are present in the formulas for calculating the corresponding criteria.
Thus, in order to correctly interpret the results of statistical studies and understand where all the indicators come from, which we get when using even such a simple criterion as a one-sample t-test, any researcher needs to understand well what mathematical ideas lie at the basis of statistical methods.
Online statistics courses: explaining difficult topics in simple language
Based on the experience of teaching statistics at the Institute of Bioinformatics , we had the idea to create a series of online courses on data analysis, in which the most important topics will be explained in accessible form for each, understanding of which is necessary for confident use of statistics methods in solving various types of problems. In 2015, we launched the Fundamentals of Statistics course, to which about 17 thousand people have registered today, three thousand students have already received a certificate of its successful completion, and the course itself was awarded the EdCrunch Awards and was recognized as the best technical course. This year, the continuation of the Fundamentals of Statistics course was launched on the stepik.org platform . Part two , in which we continue to get acquainted with the basic methods of statistics and analyze the most complex theoretical issues. By the way, one of the main topics of the course is the role of the Pearson Chi-square distribution when testing statistical hypotheses. So if you still have questions about why we subtract a unit from the total number of observations, we are waiting for you on the course!
It is also worth noting that theoretical knowledge in the field of statistics will definitely be useful not only to those who use statistics for academic purposes, but also to those who use data analysis in applied fields. Basic knowledge in the field of statistics is simply necessary for mastering more complex methods and approaches used in the field of machine learning and Data Mining. Thus, the successful completion of our courses on introducing statistics is a good start in the field of data analysis. Well, if you are seriously thinking about acquiring data skills, we think you might be interested in our online data analysis program, which we wrote about in more detail here . These statistics courses are part of this program and will allow you to seamlessly plunge into the world of statistics and machine learning. However, those who wish can take these courses without deadlines outside the context of the data analysis program.
Source: https://habr.com/ru/post/311354/
All Articles