Using autoencoders to build a recommendation system
As in many recommender systems, we have products, users, and ratings that users post (explicitly or implicitly) to products. Our task is to predict ratings for products that have not yet been rated by the user and thereby predict those products that can be highly appreciated by users, or products that may be of interest to users. (What is the function of the recommendation system is to find products that may be potentially interesting to the user.)
It was necessary to develop a recommendation system that would:
As in any classical recommendation system, we have: products, users, and user ratings of products.
')
For each product and user, we define an N-dimensional vector. Those. each product and each user is represented by a point in N-dimensional space. We use two spaces. One for users, the second - for products. (Vector identifiers of users and products.)
We also use data about the user, product, evaluation when building a model and when getting the results of product evaluations for users.
For example, for the MovieLens 1M dataset we use:
(See the source code of the demonstration .) Also note that vectors of user and product identifiers (size N) are still used.
Such data heuristically allow you to make more accurate estimates of products for users. This data is converted into vectors:
To obtain N-dimensional vectors for each product / user, we use the following scheme using autoencoders.
Let me remind you that autoencoder learns to compress data submitted to its inputs and present the input data in a compressed form.
We use two autoencoders. At the input (and as a target value) we submit a list of M (the number is 5-7) records, each of which represents:
Thus, in the process of learning (at each step of learning), autoencoders at inputs (and target values) get a list of M scores:
We also get that the first autoencoder encodes the product ID vector, and the second encodes the user ID vector .
In the minimal case, we can specify (for the first autoencoder) only the user ID and rating vector. And for the second autoencoder, only the product identifier and rating vector. Those. omit user, product, and rating data. As shown in Figure 1.
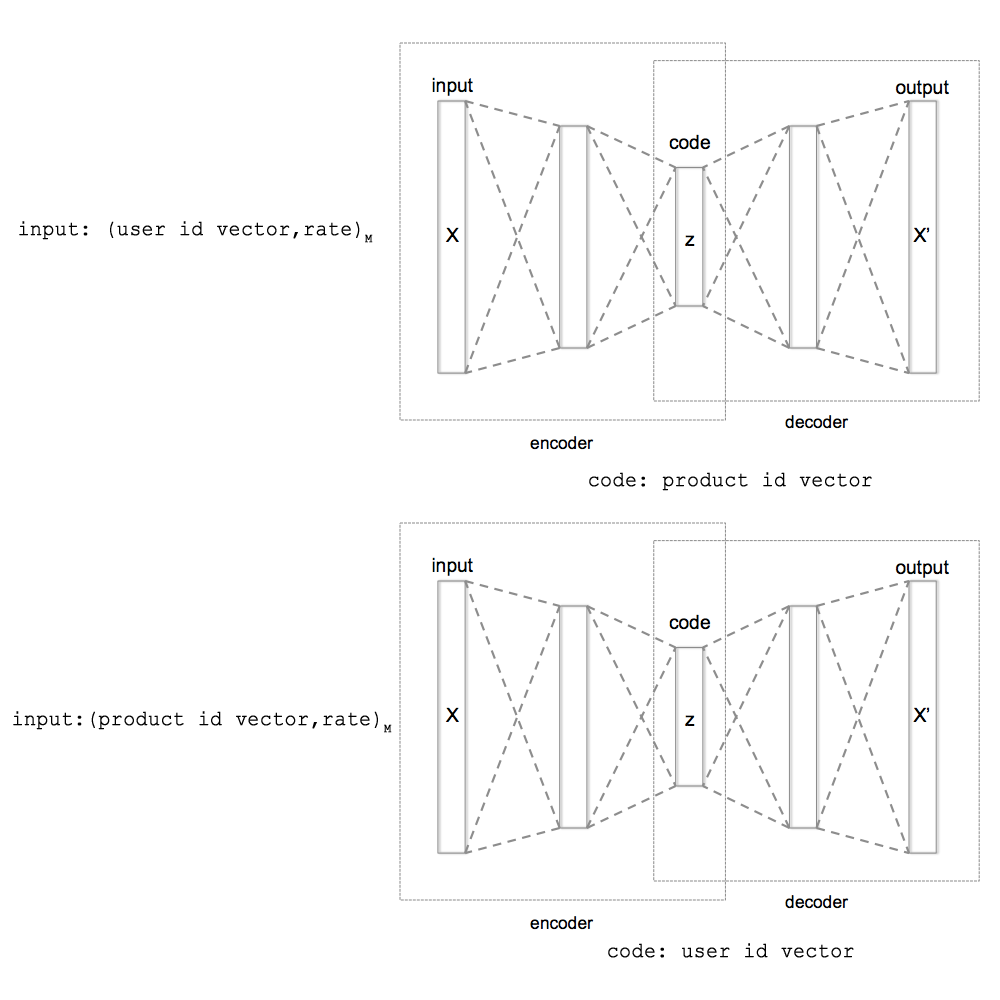
Fig. 1. Scheme of autoencoder training with the use of minimum data for training (only the vector of user identifiers, the vector of product identifiers and evaluation). As well as a scheme for obtaining identifier vectors when encoding autoencoders.
They are obtained as follows. After several learning cycles of autoencoders (about 100..1000), we set the second autoencoder values for the product ratings by one user (for each user, we set K different variants (the number is about 24..64) or user rating values for one product for first autroencoder
Suppose that for one user we set K variants of (random) product ratings (the second autoencoder), i.e. formed K different inputs for autoencoder. At the same time, we obtained K different compressed values obtained by autoencoder operation. (Ie, we received K vectors of partial user identifiers) (It is clear that we should build an autoencoder that would have a middle layer consisting of N elements, that is, would be equal to the size of the user / product identifier vector.) We find the average of these K values. This will be the new value of the user ID vector, to which we will move from the current value of the user ID vector. This is what we do for some number (L1) of users, and we get L1 averages.
Similarly, we get L2 compressed average and autoencoder trained on user ratings (or encoding product identifiers).
If we initially use random values of user and product identifier vectors, then we can move from our initial values to the L1 and L2 compressed average values (compressed average will be new target identifier vectors).
We use heuristic smooth motion to target values of identifiers. We gradually change the vector identifiers of users and products to the obtained target values of the vector identifiers of users and products.
In order to obtain satisfactory values for the vectors of identifiers of users and products, one more aspect of the work of autoencoders must be taken into account - the “breathing” of coded values or the group floating of values within certain limits. During the "breathing" of the coded values of autoencoders, all the obtained values shift by some displacement during training. As a result, if we use the coded values without any correction, then the identifier vectors will be difficult to converge. This task is quite easily solved. How this is done I do not describe in detail. This moment is solved by finding the average displacements of the new received vectors of users / products identifiers relative to the previous value of the vectors of users / products identifiers. And further, the previous values of the identifier vectors are corrected without taking into account the average mixing. (See the source code of the demonstration for more information.)
When we have identifiers, they are ordered in the N-dimensional space of users or products. Close products / users (based on user ratings) are at a short distance (Euclidean metric). Next, we can use the neural network to obtain the prediction function by: 1) a vector product identifier; 2) product information; 3) data on the possible evaluation of the product (not the evaluation itself, but this, for example, the day of the week / time when the user wants to see / have already watched the film); 4) vector user ID; 5) information about the user. Using all this data, we train the neural network to predict estimates (estimates) that a user can give to a given product under given conditions.
We repeat the training of autoencoders and neural networks to approximate the user evaluation function of the product. There are some nuances of learning to start autoencoders from random starting values. The proposed heuristics for solving these problems can be found in the proposed source code for the article.
After training, we get a model consisting of user identifiers and products from neural networks - two autoencoders and a neural network for prediction of evaluation.
After learning the system, we can predict ratings for products that are not rated by users. But also an important point is the possibility that we can:
To calculate the vectors of new identifiers, we use autoencoders from the resulting model. In this case, we use the same process as the process of obtaining the vectors of identifiers when training the model, except that we do not train the encoders with new data, but only calculate the identifiers.
The process of calculating identifiers can also be used when new assessments appear. In this case, we can adjust the identifiers. Within the framework of the already trained model, i.e. again, not retraining / not training autoencoders.
When calculating / adjusting identifiers, we, of course, do not adjust part of the model defined by neural networks for the purposes of processing speed. But new data can also change / expand the model, so such a change / expansion cannot be expressed only in the calculation of the vectors of users / products identifiers, therefore a good heuristic can be additional training of the model after a certain time interval (once a day / week / month / quarter ). Such additional training can be done in parallel with the normal operation of the system in the framework of predicting ratings, adding new products, users, adding new ratings.
In addition to solving the problems posed in the problem formulation, this approach also makes it possible to introduce memory into machine learning systems. Here, the memory can be understood directly as the values of the calculated identifiers. Within the framework of the model, they can represent objects of the external world, carrying in themselves some description of the object of the external world from the point of view of the system (some estimates of the system to these objects). Such a memory can be used to describe an object.
In addition, this approach makes it possible to set a large number of parameters that determine the vectors of identifiers of users and products, as well as evaluation parameters. (Perhaps in this case it makes sense to use heuristics to specify the degree of influence of certain data on the learning process.)
" Source code demonstration of the recommender system for this approach
It was necessary to develop a recommendation system that would:
- It was optimal in terms of speed of work after training the model.
- It would require a minimum cost of processing new incoming data. Those. so that the recommendation system would not require complete retraining or additional training after receiving new data or that operations of this kind would be minimal (perhaps we would lose in the quality of work, but it would not require significant costs for re-building the model).
Decision
Basic concepts of the proposed solution
As in any classical recommendation system, we have: products, users, and user ratings of products.
')
For each product and user, we define an N-dimensional vector. Those. each product and each user is represented by a point in N-dimensional space. We use two spaces. One for users, the second - for products. (Vector identifiers of users and products.)
We also use data about the user, product, evaluation when building a model and when getting the results of product evaluations for users.
For example, for the MovieLens 1M dataset we use:
- such data about the user as, gender of the user and age (vector size of 2 elements);
- or for the film (product) we use the year of film creation (vectors of unit length);
- and for the set assessment, on what day of the week it was set (vector of unit length).
(See the source code of the demonstration .) Also note that vectors of user and product identifiers (size N) are still used.
Such data heuristically allow you to make more accurate estimates of products for users. This data is converted into vectors:
- user data;
- product data;
- assessment data;
- the score itself or the scores of scores.
Use autoencoder
To obtain N-dimensional vectors for each product / user, we use the following scheme using autoencoders.
Let me remind you that autoencoder learns to compress data submitted to its inputs and present the input data in a compressed form.
We use two autoencoders. At the input (and as a target value) we submit a list of M (the number is 5-7) records, each of which represents:
- For autoencoder, which is trained on user rating data , we use the following values: 1) user ID vector; 2) data about the user who assessed the product (user data vector); 3) assessment data that the user has set for this product (vector of assessment data); 4) the estimates themselves (the vector of assessment values). Moreover, for this autoencoder, all values are set for one product (for one training cycle), although for different ratings (which we have in the system) of users of this product. (For MovieLens1M data, we define M records of the form: 1) a vector of N values — a vector of a user; 2) a vector of 2 values — data about a user; 3) a vector of one value - the day of the week of grading; 4) the vector of one value - the assessment itself. Those. we set the M * (N + 2 + 1 + 1) values to the inputs of the autoencoder in the case of MovieLens1M.)
- For autoencoder, which is trained on data about product ratings , we use the values: 1) product identifier vector (vector of N elements); 2) product data that the user has rated (product data vector); 3) data assessment of the product by the user (assessment data vector); 4) the estimates themselves (the vector of assessment / estimates). In this case, all values are set for one user and for different products that were rated by this user.
Thus, in the process of learning (at each step of learning), autoencoders at inputs (and target values) get a list of M scores:
- For one product - M user ratings, rated this product (in the first autoencoder).
- For one user - M ratings of products rated by this user (in the second autoencoder).
We also get that the first autoencoder encodes the product ID vector, and the second encodes the user ID vector .
In the minimal case, we can specify (for the first autoencoder) only the user ID and rating vector. And for the second autoencoder, only the product identifier and rating vector. Those. omit user, product, and rating data. As shown in Figure 1.

Fig. 1. Scheme of autoencoder training with the use of minimum data for training (only the vector of user identifiers, the vector of product identifiers and evaluation). As well as a scheme for obtaining identifier vectors when encoding autoencoders.
How to get vector identifiers of users and products
They are obtained as follows. After several learning cycles of autoencoders (about 100..1000), we set the second autoencoder values for the product ratings by one user (for each user, we set K different variants (the number is about 24..64) or user rating values for one product for first autroencoder
Suppose that for one user we set K variants of (random) product ratings (the second autoencoder), i.e. formed K different inputs for autoencoder. At the same time, we obtained K different compressed values obtained by autoencoder operation. (Ie, we received K vectors of partial user identifiers) (It is clear that we should build an autoencoder that would have a middle layer consisting of N elements, that is, would be equal to the size of the user / product identifier vector.) We find the average of these K values. This will be the new value of the user ID vector, to which we will move from the current value of the user ID vector. This is what we do for some number (L1) of users, and we get L1 averages.
Similarly, we get L2 compressed average and autoencoder trained on user ratings (or encoding product identifiers).
If we initially use random values of user and product identifier vectors, then we can move from our initial values to the L1 and L2 compressed average values (compressed average will be new target identifier vectors).
We use heuristic smooth motion to target values of identifiers. We gradually change the vector identifiers of users and products to the obtained target values of the vector identifiers of users and products.
In order to obtain satisfactory values for the vectors of identifiers of users and products, one more aspect of the work of autoencoders must be taken into account - the “breathing” of coded values or the group floating of values within certain limits. During the "breathing" of the coded values of autoencoders, all the obtained values shift by some displacement during training. As a result, if we use the coded values without any correction, then the identifier vectors will be difficult to converge. This task is quite easily solved. How this is done I do not describe in detail. This moment is solved by finding the average displacements of the new received vectors of users / products identifiers relative to the previous value of the vectors of users / products identifiers. And further, the previous values of the identifier vectors are corrected without taking into account the average mixing. (See the source code of the demonstration for more information.)
Getting product ratings for a user
When we have identifiers, they are ordered in the N-dimensional space of users or products. Close products / users (based on user ratings) are at a short distance (Euclidean metric). Next, we can use the neural network to obtain the prediction function by: 1) a vector product identifier; 2) product information; 3) data on the possible evaluation of the product (not the evaluation itself, but this, for example, the day of the week / time when the user wants to see / have already watched the film); 4) vector user ID; 5) information about the user. Using all this data, we train the neural network to predict estimates (estimates) that a user can give to a given product under given conditions.
Model building
We repeat the training of autoencoders and neural networks to approximate the user evaluation function of the product. There are some nuances of learning to start autoencoders from random starting values. The proposed heuristics for solving these problems can be found in the proposed source code for the article.
After training, we get a model consisting of user identifiers and products from neural networks - two autoencoders and a neural network for prediction of evaluation.
Work with the system after receiving the model
After learning the system, we can predict ratings for products that are not rated by users. But also an important point is the possibility that we can:
- Add new ratings and adjust user and product identifier vectors.
- Add new products and new users. Those. calculate identifier vectors for new users and products.
To calculate the vectors of new identifiers, we use autoencoders from the resulting model. In this case, we use the same process as the process of obtaining the vectors of identifiers when training the model, except that we do not train the encoders with new data, but only calculate the identifiers.
The process of calculating identifiers can also be used when new assessments appear. In this case, we can adjust the identifiers. Within the framework of the already trained model, i.e. again, not retraining / not training autoencoders.
When calculating / adjusting identifiers, we, of course, do not adjust part of the model defined by neural networks for the purposes of processing speed. But new data can also change / expand the model, so such a change / expansion cannot be expressed only in the calculation of the vectors of users / products identifiers, therefore a good heuristic can be additional training of the model after a certain time interval (once a day / week / month / quarter ). Such additional training can be done in parallel with the normal operation of the system in the framework of predicting ratings, adding new products, users, adding new ratings.
What gives the proposed approach
In addition to solving the problems posed in the problem formulation, this approach also makes it possible to introduce memory into machine learning systems. Here, the memory can be understood directly as the values of the calculated identifiers. Within the framework of the model, they can represent objects of the external world, carrying in themselves some description of the object of the external world from the point of view of the system (some estimates of the system to these objects). Such a memory can be used to describe an object.
In addition, this approach makes it possible to set a large number of parameters that determine the vectors of identifiers of users and products, as well as evaluation parameters. (Perhaps in this case it makes sense to use heuristics to specify the degree of influence of certain data on the learning process.)
" Source code demonstration of the recommender system for this approach
Source: https://habr.com/ru/post/311232/
All Articles