Data structures for the smallest
James Kyle once took and wrote a post about data structures, adding their implementation to JavaScript. And I took and translated.
Disclaimer: in a post a lot of ascii-graphics. You should not read it from a mobile device - text formatting will disappoint you.
')
Today we will learn all about data structures.
“Oooooo, how interesting ...”, yes?
Yeah, not the most juicy topic of this day, but extremely important. Not to take courses like CS101, but to better understand programming.
Knowledge of data structures will help you:
I think the first is more important. The correct data structure can drastically simplify the code, eliminating confusing logic.
The second point is also important. When taking into account the performance or memory of the program, the correct choice of data structure significantly affects the work.
To get acquainted with data structures, we will implement some of them. Do not worry, the code will be concise. In fact, there are more comments here, and the code between them - just one, two, and I got it.
In essence, these are ways to store and organize data in order to more effectively solve various tasks. Data can be presented in different ways. Depending on what the data is and what you are going to do with it, one idea will work better than others.
To understand why this is happening, let's first talk about algorithms.
Algorithm is such a smart name for the sequence of actions performed.
Data structures are implemented using algorithms, algorithms using data structures. Everything consists of data structures and algorithms, down to the level at which microscopic little men run punched cards and make the computer work. (Well, yes, Intel has microscopic people in service. Get up, people!)
Any given task is implemented in an infinite number of ways. As a consequence, to solve common problems invented a variety of different algorithms.
For example, to sort an unordered set of elements, a ridiculously large number of algorithms exist:
Some of them are much faster than others. Others take up less memory. Still others are easy to implement. The fourth is built on assumptions about data sets.
Each of the sorts is better suited for a particular task. Therefore, you will need to first decide what your needs and criteria are in order to understand how to compare the algorithms with each other.
To compare the performance of the algorithms, a rough measurement of the average performance and performance in the worst case is used, which is denoted by the term “O” large.
“O” is large - designation of a method of approximate evaluation of the performance of algorithms for relative comparison.
About big - the mathematical designation borrowed by computer science, defining how algorithms correspond with a certain amount of N data transferred by it.
About large characterizes two main quantities:
Estimated execution time is the total number of operations that the algorithm will perform on a given data set.
Volume estimation is the total amount of memory required by the algorithm for processing a given set of data.
Estimates are made independently of one another: some algorithms can perform fewer operations than others, while taking up more memory. Having defined your requirements, you can choose the appropriate algorithm.
Here are some common values about big:
To give an idea of what orders of numbers we are talking about, let's take a look at what these values will be depending on N.
As you can see, even with relatively small numbers, you can do * dofig * additional work.
Data structures allow 4 basic types of actions: access, search, insert and delete.
I note that data structures may be good in one of the actions, but bad in the other.
Or even…
In addition, some actions have different "average" performance and performance in the "worst case".
An ideal data structure does not exist. You choose the most appropriate, based on the data and how they will be processed. To make the right choice, it is important to know the various common data structures.
Computer memory is a pretty boring thing. This is a group of ordered slots in which information is stored. To access it, you must know its address in memory.
A fragment of memory can be represented as follows:
If you wondered why in programming languages, counting starts from 0 - because memory works that way. To read the first fragment of memory, you read from 0 to 1, the second - from 1 to 2. The addresses of these fragments are respectively 0 and 1.
Of course, there is more memory in the computer than shown in the example, but its device continues the principle of the template considered.
The vastness of memory is like the Wild West. Each program running on a computer is stored within the same * physical * data structure. The use of memory is a difficult task, and there are additional levels of abstraction for convenient work with it.
Abstractions have two additional purposes:
- Store data in memory in such a way that it is efficient and / or fast to work with.
- Store data in memory so that it is easier to use.
To begin with, we will implement a list to show the complexity of the interaction between the memory and the data structure.
A list is a representation of a numbered sequence of values, where the same value may be present as many times as desired.
Let's start with an empty block of memory, represented by a regular JavaScript array. We also need to store the value of the length of the list.
Notice that we want to store the length separately, since in reality “memory” does not have a length value that could be taken and read.
The first step is to get the data from the list. A regular list allows you to quickly access memory, since you already know the address you need.
The complexity of the operation of access to the list - O (1) - "WELL !!"
Lists have sequence numbers, so you can insert values at the beginning, middle, and end.
We will focus on adding and removing values at the beginning or end of the list. For this you need 4 methods:
Let's start with the “push” operation - we implement the addition of elements to the end of the list.
This is as easy as adding a value to the address following our list. Since we store the length, it’s easy to calculate the address. Add a value and increase the length.
Adding an element to the end of the list - the constant O (1) - "WELL !!"
Comments Habra: poxu does not agree with the author and explains that there is a memory expansion operation that increases the complexity of adding items to the list.
Next, we implement the pop method, which removes an element from the end of our list. Similar to push, all you have to do is remove the value from the last address. Well, and reduce the length.
Deleting an element from the end of the list - the constant O (1) - “OK!”
Push and pop work with the end of the list, and in general are simple operations, since they do not affect the rest of the list.
Let's see what happens when we work with the beginning of the list, with the operations “unshift” and “shift”.
To add a new item to the top of the list, you need to free up space for this value by sliding all subsequent values by one.
To make such a shift, you need to go through each of the elements and put the previous one in its place.
Because we have to go through each of the list items:
Adding an element to the top of the list - linear O (N) - “NORMAS.”
It remains to write the list shift function in the opposite direction - shift.
We delete the first value and then shift each item in the list to the previous address.
Deleting an element from the beginning of the list - linear O (N) - “NORMAS.”
Lists do an excellent job with quick access to items at their end and working with them. However, as we have seen, for the elements from the beginning or the middle, they are not too good, as you have to manually handle memory addresses.
Let's look at a different data structure and its methods for adding, accessing and deleting values without having to know the addresses of the elements.
A hash table is an unordered data structure. Instead of indexes, we work with “keys” and “values”, calculating the memory address by key.
The point is that the keys are “hashed” and allow you to work effectively with memory — add, receive, modify, and delete values.
Again, use a regular JavaScript array representing memory.
To save key-value pairs from a hash table into memory, you need to turn keys into addresses. This is the operation of "hashing".
It accepts a key as input and converts it into a unique number corresponding to that key.
Such an operation requires caution. If the key is too large, it will be mapped to a non-existent address in memory.
Therefore, the hash function should limit the size of the keys, i.e. limit the number of available memory addresses for an unlimited number of values.
Any implementation of hash tables faces this problem.
However, since we are going to consider only the structure of their work, let us assume that there will be no collisions.
Let's define the function "hashKey".
Do not go into the internal logic, just believe that it accepts a string as an input and returns (almost always) a unique address that we will use in the remaining functions.
Now we define the function “get”, which gets the value by key.
The difficulty of reading the values from the hash table - the constant O (1) - “OK” !!
Before you receive the data, it would be nice to add them first. The “set” function will help us with this.
The difficulty of setting the value in the hash table - the constant O (1) - "OK" !!
Finally, we need a way to remove values from the hash table. The difficulty of deleting a value from the hash table is the O (1) constant - “OK!”
Now we will stop working with memory directly: all subsequent data structures will be implemented through other data structures.
New structures focus on two things:
The purpose of such data structures is to organize information for use in programs of various types. They provide a language for expressing more complex logic. In this case, implementation details are abstracted, i.e. You can change the implementation by making it faster.
Stacks are like lists. They are also ordered, but limited in actions: you can only add and remove values from the end of the list. As we saw earlier, this happens very quickly if you access memory directly.
However, stacks can be implemented through other data structures to provide additional functionality.
The most common example of using stacks is that you have one process that adds items to the stack and a second that removes them from the end — prioritizing recently added items.
We again need a JavaScript array, but this time it symbolizes not a memory, but a list, like the one implemented above.
We will need to implement two methods that are functionally identical to the list methods, “push” and “pop”.
Push adds items to the top of the stack.
Pop removes items from the top.
In addition, we will add a peek function that shows an element at the top of the stack without deleting it. Note translator: peek - take a look.
Now create a queue - a structure that is complementary to the stack. The difference is that the elements of the queue are removed from the beginning, not from the end, i.e. first the old elements, then the new ones.
As already discussed, since the functionality is limited, there are different queue implementations. A good way would be to use a linked list, which we will talk about later.
And once again we call for help JavaScript array! In the case of a queue, we again consider it as a list, not as a memory.
Similar to stacks, we define two functions for adding and removing items from the queue.
The first is “enqueue” - adding an item to the end of the list.
Next - “dequeue”. The element is removed not from the end of the list, but from the beginning.
Similarly to the stacks, we declare the function “peek”, which allows to get the value at the beginning of the queue without deleting it.
It is important to note that since the list was used to implement the queue, it inherits the linear performance of the shift method (that is, O (N) - “NORMAS.”).
As we will see later, linked lists allow you to implement a faster queue.
From this point on, we will work with data structures where values refer to each other.
The elements of the data structure become mini-structures themselves, containing the value and additional information - references to other elements of the parent structure.
Now you understand what I mean.
In fact, the graph is not at all what you thought when you saw the ascii graph.
A graph is a structure like this:
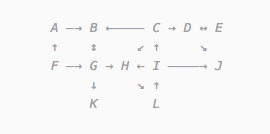
We have a lot of “vertices” (A, B, C, D, ...) connected by lines.
These peaks can be represented like this:
And the whole graph will look like this:
Imagine a vertex list with a javascript array. The array is not used for the purpose of specifically organizing vertices, but as a place to store vertices.
Let's start adding values to the graph, creating vertices without any lines.
Now we need a way to search for vertices in the graph. Usually, to speed up the search, another data structure is made on top of the graph.
But in our case, we simply iterate through all the vertices to find the corresponding value. The way is slow, but working.
Now we can connect two vertices by drawing a “line” from one to another (approx. Translator: arc of a graph).
The resulting graph can be used like this:
It seems that too much work has been done for such a small task, but this is a powerful pattern.
It is often used to maintain transparency in complex programs. This is achieved by optimizing the relationships between the data, rather than the operations on the data itself. If you select one vertex in the graph, it is incredibly easy to find related items.
Graphs can represent a lot of things: users and their friends, 800 dependencies in the node_modules folder, even the Internet itself, which is a graph of web pages linked to each other by links.
Let's now see how a graph-like structure can optimize an ordered list of data.
Linked lists are a common data structure, often used to implement other structures. The advantage of a linked list is the efficiency of adding elements to the beginning, middle and end.
A linked list is inherently similar to a graph: you work with vertices pointing to other vertices. They are arranged in this way:
If you imagine this structure in the form of JSON, you get something like this:
Unlike the graph, a linked list has a single vertex from which the inner chain begins. It is called the "head", the head element, or the first element of the linked list.
We are also going to track the length of the list.
The first thing you need is a way to get the value for this position.
Unlike regular lists, we cannot jump to the desired position. Instead, we must go to it through separate vertices.
Now we need a way to add vertices to the selected position.
Create an add method that takes a value and a position.
The last method we need is remove. Find the top by position and throw it out of the chain.
The two remaining data structures belong to the family of "trees".
As in life, there are many different tree data structures.
Notetranslator: well, not-ee, I pass ...
Binary Trees:
AA Tree, AVL Tree, Binary Search Tree, Binary Tree, Cartesian Tree, sibling tree, order statistics tree, Pagoda, ...
B Trees:
B Tree, B + Tree, B * Tree, B Sharp Tree, Dancing Tree, 2-3 Tree, ...
Heaps:
Heap, Binary Heap, Weak Heap, Binomial Heap, Fibonacci Heap, Leonardo Heap, 2-3 Heap, Soft Heap, Pairing Heap, Leftist Heap, Treap,…
Trees:
Trie, Radix Tree, Suffix Tree, Suffix Array, FM-index, B-trie,…
Multi-way Trees:
Ternary Tree, K-ary tree, And-or tree, (( a, b) -tree, Link / Cut Tree, ...
Space Partitioning Trees:
Segment Tree, Interval Tree, Range Tree, Bin, Kd Tree, Quadtree, Octree, Z-Order, UB-Tree, R-Tree, X-Tree, Metric Tree, Cover Tree, ...
Application-Specific Trees:
Abstract Syntax Tree, Parse Tree, Decision Tree, Minimax Tree, ...
What you really did not expect is that you will study dendrology today ... And this is not all trees. Let them not confuse you, most of them do not make sense at all. It was necessary for people to somehow defend their candidate degrees and prove something for this.
Trees are similar to graphs or linked lists, with the difference that they are “unidirectional”. This means that there can be no circular references in them.

If you can walk a circle through the treetops ... well, congratulations, but this is not a tree.
Trees are used in a variety of tasks. They are used to optimize search or sorting. They can better organize the program. They can create a view that is easier to work with.
Let's start with a simple tree structure. There are no special rules in it, and it looks like this:
The tree must begin with a single parent, the "root" of the tree.
We need a way to bypass our tree and call a specific function at each of its vertices.
Now we need a way to add vertices to the tree.
This is a simple tree, perhaps useful only when the data displayed is similar to it.
However, with additional rules, trees can perform a bunch of different tasks.
Binary search trees are a common form of trees. They can effectively read, search, insert and delete values, while maintaining the sorted order.
Imagine that you have a sequence of numbers:
Let's turn it into a tree, starting from the center.
Here is an example of how a binary tree works. Each vertex has two descendants:
Note: in order for this to work, all values in the tree must be unique.
This makes traversing the tree when searching for a value very effective. For example, try to find the number 5 in our tree.
Notice, to get to 5, it took only 3 checks. And if the tree consisted of 1000 elements, the path would be as follows:
Only 10 checks on 1000 items!
Another important feature of binary search trees is their similarity with linked lists — when adding or removing a value, you only need to update the immediately surrounding elements.
As in the previous section, you first need to set the “root” of the binary search tree.
To check if the value is in the tree, you need to search the tree.
To add an element to the tree, you need to make the same traversal as before, jumping over the left and right vertices, depending on whether they are larger or smaller than the value added.
However, now, when we get to the left or right vertex of null,
we will add a vertex to this position.
I hope you got a good dose of knowledge. If you like it,
put asterisks in the repository and follow me on twitter.
You can also read my other article, “The Super Tiny Compiler” github.com/thejameskyle/the-super-tiny-compiler
Also this article can be read on githabe .
Translation: aalexeev , editing: iamo0 , Chaika Chursina.
Disclaimer: in a post a lot of ascii-graphics. You should not read it from a mobile device - text formatting will disappoint you.

')
Today we will learn all about data structures.
“Oooooo, how interesting ...”, yes?
Yeah, not the most juicy topic of this day, but extremely important. Not to take courses like CS101, but to better understand programming.
Knowledge of data structures will help you:
- Manage the complexity of their programs, making them more accessible to understand.
- Create high-performance programs that work efficiently with memory.
I think the first is more important. The correct data structure can drastically simplify the code, eliminating confusing logic.
The second point is also important. When taking into account the performance or memory of the program, the correct choice of data structure significantly affects the work.
To get acquainted with data structures, we will implement some of them. Do not worry, the code will be concise. In fact, there are more comments here, and the code between them - just one, two, and I got it.
============================================================================ ,.-'`'-.,.-'`'-.,.-'`'-.,.-'`'-.,.-'`'-.,.-'`'-.,.-'`'-.,.-'`'-.,.-'`'-.,.-' ============================================================================
============================================================================ ,.-'`'-.,.-'`'-.,.-'`'-.,.-'`'-.,.-'`'-.,.-'`'-.,.-'`'-.,.-'`'-.,.-'`'-.,.-' ============================================================================
What are data structures?
In essence, these are ways to store and organize data in order to more effectively solve various tasks. Data can be presented in different ways. Depending on what the data is and what you are going to do with it, one idea will work better than others.
To understand why this is happening, let's first talk about algorithms.
/*** ===================================================================== ***\ * * * ,--,--. ,--,--. * * ,----------. | | | | | | _____ * * |`----------'| | | | | | | | | ,------. * * | | | | | | | | ,--. | oo | |`------'| * * | | ,| +-|-+ | | +-|-+ |` | | |_____| | | * * | | ,:==| | |###|======|###| | |====#==#====#=,, | | * * | | || `| +---+ | | +---+ |' ,,=#==#====O=`` ,| | * * | | || | | | | | | ``=#==#====#=====|| | * * `----------' || | | | | | | |__| `| | * * | | ``=| |===`` `--,',--` `--,',--` /||\ `------' * ** \_/ \_/ / / \ \ / / \ \ //||\\ |_| |_| ** \*** ===================================================================== ***/
/*** ===================================================================== ***\ * * * ,--,--. ,--,--. * * ,----------. | | | | | | _____ * * |`----------'| | | | | | | | | ,------. * * | | | | | | | | ,--. | oo | |`------'| * * | | ,| +-|-+ | | +-|-+ |` | | |_____| | | * * | | ,:==| | |###|======|###| | |====#==#====#=,, | | * * | | || `| +---+ | | +---+ |' ,,=#==#====O=`` ,| | * * | | || | | | | | | ``=#==#====#=====|| | * * `----------' || | | | | | | |__| `| | * * | | ``=| |===`` `--,',--` `--,',--` /||\ `------' * ** \_/ \_/ / / \ \ / / \ \ //||\\ |_| |_| ** \*** ===================================================================== ***/
Algorithms
Algorithm is such a smart name for the sequence of actions performed.
Data structures are implemented using algorithms, algorithms using data structures. Everything consists of data structures and algorithms, down to the level at which microscopic little men run punched cards and make the computer work. (Well, yes, Intel has microscopic people in service. Get up, people!)
Any given task is implemented in an infinite number of ways. As a consequence, to solve common problems invented a variety of different algorithms.
For example, to sort an unordered set of elements, a ridiculously large number of algorithms exist:
Sorting by inserts, Sorting by sorting, Merge sorting, Bubble sorting, Heap sorting, Quick sorting, Shell sorting, Tim sorting, Block sorting, Bit sorting ...
Some of them are much faster than others. Others take up less memory. Still others are easy to implement. The fourth is built on assumptions about data sets.
Each of the sorts is better suited for a particular task. Therefore, you will need to first decide what your needs and criteria are in order to understand how to compare the algorithms with each other.
To compare the performance of the algorithms, a rough measurement of the average performance and performance in the worst case is used, which is denoted by the term “O” large.
/*** ===================================================================== ***\ * abd * * ab O(N^2) d * * O(N!) ab O(N log N) dc * * abdc * * abdc O(N) * * abdc * * abdc * * abdc * * ab c O(1) * * eeee ec deeeeeeee * * ba cd * * ba cdfffffff * ** cadf fdfffff O(log N) ** \*** ===================================================================== ***/
/*** ===================================================================== ***\ * abd * * ab O(N^2) d * * O(N!) ab O(N log N) dc * * abdc * * abdc O(N) * * abdc * * abdc * * abdc * * ab c O(1) * * eeee ec deeeeeeee * * ba cd * * ba cdfffffff * ** cadf fdfffff O(log N) ** \*** ===================================================================== ***/
O great
“O” is large - designation of a method of approximate evaluation of the performance of algorithms for relative comparison.
About big - the mathematical designation borrowed by computer science, defining how algorithms correspond with a certain amount of N data transferred by it.
About large characterizes two main quantities:
Estimated execution time is the total number of operations that the algorithm will perform on a given data set.
Volume estimation is the total amount of memory required by the algorithm for processing a given set of data.
Estimates are made independently of one another: some algorithms can perform fewer operations than others, while taking up more memory. Having defined your requirements, you can choose the appropriate algorithm.
Here are some common values about big:
, ---------------------------------------------------------------------------- O(1) !! O(log N) ! O(N) . - O(N log N) ... O(N ^ 2) O(2 ^ N) O(N!) To give an idea of what orders of numbers we are talking about, let's take a look at what these values will be depending on N.
N = 5 10 20 30 ----------------------------------------------------------------------- O(1) 1 1 1 1 O(log N) 2.3219... 3.3219... 4.3219... 4.9068... O(N) 5 10 20 30 O(N log N) 11.609... 33.219... 84.638... 147.204... O(N ^ 2) 25 100 400 900 O(2 ^ N) 32 1024 1,048,576 1,073,741,824 O(N!) 120 3,628,800 2,432,902,0... 265,252,859,812,191,058,636,308,480,000,000 As you can see, even with relatively small numbers, you can do * dofig * additional work.
Data structures allow 4 basic types of actions: access, search, insert and delete.
I note that data structures may be good in one of the actions, but bad in the other.
------------------------------------------------------------------------ O(1) O(N) O(N) O(N) O(N) O(N) O(1) O(1) O(log N) O(log N) O(log N) O(log N) Or even…
------------------------------------------------------------------------ In addition, some actions have different "average" performance and performance in the "worst case".
An ideal data structure does not exist. You choose the most appropriate, based on the data and how they will be processed. To make the right choice, it is important to know the various common data structures.
/*** ===================================================================== ***\ * _.-.. * * ,'9 )\)`-.,.--. * * `-.| `. * * \, , \) * * `. )._\ (\ * * |// `-,// * * ]|| //" * ** hjw "" "" ** \*** ===================================================================== ***/
/*** ===================================================================== ***\ * _.-.. * * ,'9 )\)`-.,.--. * * `-.| `. * * \, , \) * * `. )._\ (\ * * |// `-,// * * ]|| //" * ** hjw "" "" ** \*** ===================================================================== ***/
Memory
Computer memory is a pretty boring thing. This is a group of ordered slots in which information is stored. To access it, you must know its address in memory.
A fragment of memory can be represented as follows:
: |1001|0110|1000|0100|0101|1010|0010|0001|1101|1011... : 0 1 2 3 4 5 6 7 8 9 ...
: |1001|0110|1000|0100|0101|1010|0010|0001|1101|1011... : 0 1 2 3 4 5 6 7 8 9 ...
If you wondered why in programming languages, counting starts from 0 - because memory works that way. To read the first fragment of memory, you read from 0 to 1, the second - from 1 to 2. The addresses of these fragments are respectively 0 and 1.
Of course, there is more memory in the computer than shown in the example, but its device continues the principle of the template considered.
The vastness of memory is like the Wild West. Each program running on a computer is stored within the same * physical * data structure. The use of memory is a difficult task, and there are additional levels of abstraction for convenient work with it.
Abstractions have two additional purposes:
- Store data in memory in such a way that it is efficient and / or fast to work with.
- Store data in memory so that it is easier to use.
/*** ===================================================================== ***\ * * _______________________ * * ()=(_______________________)=() * * * * | | * * | ~ ~~~~~~~~~~~~~ | * * * * * | | * * * | ~ ~~~~~~~~~~~~~ | * * * | | * * | ~ ~~~~~~~~~~~~~ | * * * * | | * * * |_____________________| * * * * ()=(_______________________)=() * ** ** \*** ===================================================================== ***/
/*** ===================================================================== ***\ * * _______________________ * * ()=(_______________________)=() * * * * | | * * | ~ ~~~~~~~~~~~~~ | * * * * * | | * * * | ~ ~~~~~~~~~~~~~ | * * * | | * * | ~ ~~~~~~~~~~~~~ | * * * * | | * * * |_____________________| * * * * ()=(_______________________)=() * ** ** \*** ===================================================================== ***/
Lists
To begin with, we will implement a list to show the complexity of the interaction between the memory and the data structure.
A list is a representation of a numbered sequence of values, where the same value may be present as many times as desired.
Let's start with an empty block of memory, represented by a regular JavaScript array. We also need to store the value of the length of the list.
Notice that we want to store the length separately, since in reality “memory” does not have a length value that could be taken and read.
class List { constructor() { this.memory = []; this.length = 0; } //... } The first step is to get the data from the list. A regular list allows you to quickly access memory, since you already know the address you need.
The complexity of the operation of access to the list - O (1) - "WELL !!"
get(address) { return this.memory[address]; } Lists have sequence numbers, so you can insert values at the beginning, middle, and end.
We will focus on adding and removing values at the beginning or end of the list. For this you need 4 methods:
- Push - Add value to the end.
- Pop - Remove value from the end.
- Unshift - Add value to the beginning.
- Shift - Remove value from the beginning.
Let's start with the “push” operation - we implement the addition of elements to the end of the list.
This is as easy as adding a value to the address following our list. Since we store the length, it’s easy to calculate the address. Add a value and increase the length.
Adding an element to the end of the list - the constant O (1) - "WELL !!"
push(value) { this.memory[this.length] = value; this.length++; } Comments Habra: poxu does not agree with the author and explains that there is a memory expansion operation that increases the complexity of adding items to the list.
Next, we implement the pop method, which removes an element from the end of our list. Similar to push, all you have to do is remove the value from the last address. Well, and reduce the length.
Deleting an element from the end of the list - the constant O (1) - “OK!”
pop() { // — . if (this.length === 0) return; // , , . var lastAddress = this.length - 1; var value = this.memory[lastAddress]; delete this.memory[lastAddress]; this.length--; // , . return value; } Push and pop work with the end of the list, and in general are simple operations, since they do not affect the rest of the list.
Let's see what happens when we work with the beginning of the list, with the operations “unshift” and “shift”.
To add a new item to the top of the list, you need to free up space for this value by sliding all subsequent values by one.
[a, b, c, d, e] 0 1 2 3 4 ⬊ ⬊ ⬊ ⬊ ⬊ 1 2 3 4 5 [x, a, b, c, d, e]
[a, b, c, d, e] 0 1 2 3 4 ⬊ ⬊ ⬊ ⬊ ⬊ 1 2 3 4 5 [x, a, b, c, d, e]
To make such a shift, you need to go through each of the elements and put the previous one in its place.
Because we have to go through each of the list items:
Adding an element to the top of the list - linear O (N) - “NORMAS.”
unshift(value) { // C , . var previous = value; // ... for (var address = 0; address < this.length; address++) { // «current» «previous», // «current» . var current = this.memory[address]; this.memory[address] = previous; previous = current; } // . this.memory[this.length] = previous; this.length++; } It remains to write the list shift function in the opposite direction - shift.
We delete the first value and then shift each item in the list to the previous address.
[x, a, b, c, d, e] 1 2 3 4 5 ⬋ ⬋ ⬋ ⬋ ⬋ 0 1 2 3 4 [a, b, c, d, e]
[x, a, b, c, d, e] 1 2 3 4 5 ⬋ ⬋ ⬋ ⬋ ⬋ 0 1 2 3 4 [a, b, c, d, e]
Deleting an element from the beginning of the list - linear O (N) - “NORMAS.”
shift() { // — . if (this.length === 0) return; var value = this.memory[0]; // , for (var address = 0; address < this.length - 1; address++) { // . this.memory[address] = this.memory[address + 1]; } // , . delete this.memory[this.length - 1]; this.length--; return value; } Lists do an excellent job with quick access to items at their end and working with them. However, as we have seen, for the elements from the beginning or the middle, they are not too good, as you have to manually handle memory addresses.
Let's look at a different data structure and its methods for adding, accessing and deleting values without having to know the addresses of the elements.
/*** ===================================================================== ***\ * ((\ * * ( _ ,-_ \ \ * * ) / \/ \ \ \ \ * * ( /)| \/\ \ \| | .'---------------------'. * * `~()_______)___)\ \ \ \ \ | .' '. * * |)\ ) `' | | | .'-----------------------------'. * * / /, | '...............................' * * ejm | | / \ _____________________ / * * \ / | |_) (_| | * * \ / | | | | * * ) / | | | | * ** / / (___) (___) ** \*** ===================================================================== ***/
/*** ===================================================================== ***\ * ((\ * * ( _ ,-_ \ \ * * ) / \/ \ \ \ \ * * ( /)| \/\ \ \| | .'---------------------'. * * `~()_______)___)\ \ \ \ \ | .' '. * * |)\ ) `' | | | .'-----------------------------'. * * / /, | '...............................' * * ejm | | / \ _____________________ / * * \ / | |_) (_| | * * \ / | | | | * * ) / | | | | * ** / / (___) (___) ** \*** ===================================================================== ***/
Hash tables
A hash table is an unordered data structure. Instead of indexes, we work with “keys” and “values”, calculating the memory address by key.
The point is that the keys are “hashed” and allow you to work effectively with memory — add, receive, modify, and delete values.
var hashTable = new HashTable(); hashTable.set('myKey', 'myValue'); hashTable.get('myKey'); // >> 'myValue' Again, use a regular JavaScript array representing memory.
class HashTable { constructor() { this.memory = []; } // ... } To save key-value pairs from a hash table into memory, you need to turn keys into addresses. This is the operation of "hashing".
It accepts a key as input and converts it into a unique number corresponding to that key.
hashKey("abc") => 96354 hashKey("xyz") => 119193 Such an operation requires caution. If the key is too large, it will be mapped to a non-existent address in memory.
Therefore, the hash function should limit the size of the keys, i.e. limit the number of available memory addresses for an unlimited number of values.
Any implementation of hash tables faces this problem.
However, since we are going to consider only the structure of their work, let us assume that there will be no collisions.
Let's define the function "hashKey".
Do not go into the internal logic, just believe that it accepts a string as an input and returns (almost always) a unique address that we will use in the remaining functions.
hashKey(key) { var hash = 0; for (var index = 0; index < key.length; index++) { // ---. var code = key.charCodeAt(index); hash = ((hash << 5) - hash) + code | 0; } return hash; } Now we define the function “get”, which gets the value by key.
The difficulty of reading the values from the hash table - the constant O (1) - “OK” !!
get(key) { // . var address = this.hashKey(key); // , . return this.memory[address]; } Before you receive the data, it would be nice to add them first. The “set” function will help us with this.
The difficulty of setting the value in the hash table - the constant O (1) - "OK" !!
set(key, value) { // . var address = this.hashKey(key); // . this.memory[address] = value; } Finally, we need a way to remove values from the hash table. The difficulty of deleting a value from the hash table is the O (1) constant - “OK!”
remove(key) { // , , . var address = this.hashKey(key); // , . if (this.memory[address]) { delete this.memory[address]; } } ============================================================================ ,.-'`'-.,.-'`'-.,.-'`'-.,.-'`'-.,.-'`'-.,.-'`'-.,.-'`'-.,.-'`'-.,.-'`'-.,.-' ============================================================================
============================================================================ ,.-'`'-.,.-'`'-.,.-'`'-.,.-'`'-.,.-'`'-.,.-'`'-.,.-'`'-.,.-'`'-.,.-'`'-.,.-' ============================================================================
Now we will stop working with memory directly: all subsequent data structures will be implemented through other data structures.
New structures focus on two things:
- Organize data based on the characteristics of their use
- Abstract implementation details
The purpose of such data structures is to organize information for use in programs of various types. They provide a language for expressing more complex logic. In this case, implementation details are abstracted, i.e. You can change the implementation by making it faster.
/*** ===================================================================== ***\ * _ . - - -- .. _ * * |||| .-' /```\ `'-_ /| * * |||| ( /`` \___/ ```\ ) | | * * \__/ |`"-//..__ __..\\-"`| | | * * || |`"||...__`````__...||"`| | | * * || |`"||...__`````__...||"`| \ | * * || _,.--|`"||...__`````__...||"`|--.,_ || * * || .'` |`"||...__`````__...||"`| `'. || * * || '. `/ |...__`````__...| \ .' || * * || `'-..__ `` ````` `` __..-'` || * * `""---,,,_______,,,---""` * ** ** \*** ===================================================================== ***/
/*** ===================================================================== ***\ * _ . - - -- .. _ * * |||| .-' /```\ `'-_ /| * * |||| ( /`` \___/ ```\ ) | | * * \__/ |`"-//..__ __..\\-"`| | | * * || |`"||...__`````__...||"`| | | * * || |`"||...__`````__...||"`| \ | * * || _,.--|`"||...__`````__...||"`|--.,_ || * * || .'` |`"||...__`````__...||"`| `'. || * * || '. `/ |...__`````__...| \ .' || * * || `'-..__ `` ````` `` __..-'` || * * `""---,,,_______,,,---""` * ** ** \*** ===================================================================== ***/
Stacks
Stacks are like lists. They are also ordered, but limited in actions: you can only add and remove values from the end of the list. As we saw earlier, this happens very quickly if you access memory directly.
However, stacks can be implemented through other data structures to provide additional functionality.
The most common example of using stacks is that you have one process that adds items to the stack and a second that removes them from the end — prioritizing recently added items.
We again need a JavaScript array, but this time it symbolizes not a memory, but a list, like the one implemented above.
class Stack { constructor() { this.list = []; this.length = 0; } // ... } We will need to implement two methods that are functionally identical to the list methods, “push” and “pop”.
Push adds items to the top of the stack.
push(value) { this.length++; this.list.push(value); } Pop removes items from the top.
pop() { // — . if (this.length === 0) return; // . this.length--; return this.list.pop(); } In addition, we will add a peek function that shows an element at the top of the stack without deleting it. Note translator: peek - take a look.
peek() { // , . return this.list[this.length - 1]; } /*** ===================================================================== ***\ * /:""| ,@@@@@@. * * |: oo|_ ,@@@@@`oo * * C _) @@@@C _) * * ) / "@@@@ '= * * /`\\ ```)/ * * || | | /`\\ * * || | | || | \ * * ||_| | || | / * * \( ) | ||_| | * * |~~~`-`~~~| |))) | * * (_) | | (_) |~~~/ (_) * * | |`""....__ __....""`| |`""...._|| / __....""`| | * * | |`""....__`````__....""`| |`""....__`````__....""`| | * * | | | ||``` | | ||`|`` | | * * | | |_||__ | | ||_|__ | | * * ,| |, jgs (____)) ,| |, ((;:;:) ,| |, * ** `---` `---` `---` ** \*** ===================================================================== ***/
/*** ===================================================================== ***\ * /:""| ,@@@@@@. * * |: oo|_ ,@@@@@`oo * * C _) @@@@C _) * * ) / "@@@@ '= * * /`\\ ```)/ * * || | | /`\\ * * || | | || | \ * * ||_| | || | / * * \( ) | ||_| | * * |~~~`-`~~~| |))) | * * (_) | | (_) |~~~/ (_) * * | |`""....__ __....""`| |`""...._|| / __....""`| | * * | |`""....__`````__....""`| |`""....__`````__....""`| | * * | | | ||``` | | ||`|`` | | * * | | |_||__ | | ||_|__ | | * * ,| |, jgs (____)) ,| |, ((;:;:) ,| |, * ** `---` `---` `---` ** \*** ===================================================================== ***/
Queues
Now create a queue - a structure that is complementary to the stack. The difference is that the elements of the queue are removed from the beginning, not from the end, i.e. first the old elements, then the new ones.
As already discussed, since the functionality is limited, there are different queue implementations. A good way would be to use a linked list, which we will talk about later.
And once again we call for help JavaScript array! In the case of a queue, we again consider it as a list, not as a memory.
class Queue { constructor() { this.list = []; this.length = 0; } // ... } Similar to stacks, we define two functions for adding and removing items from the queue.
The first is “enqueue” - adding an item to the end of the list.
enqueue(value) { this.length++; this.list.push(value); } Next - “dequeue”. The element is removed not from the end of the list, but from the beginning.
dequeue() { // — . if (this.length === 0) return; // shift . this.length--; return this.list.shift(); } Similarly to the stacks, we declare the function “peek”, which allows to get the value at the beginning of the queue without deleting it.
peek() { return this.list[0]; } It is important to note that since the list was used to implement the queue, it inherits the linear performance of the shift method (that is, O (N) - “NORMAS.”).
As we will see later, linked lists allow you to implement a faster queue.
============================================================================ ,.-'`'-.,.-'`'-.,.-'`'-.,.-'`'-.,.-'`'-.,.-'`'-.,.-'`'-.,.-'`'-.,.-'`'-.,.-' ============================================================================
============================================================================ ,.-'`'-.,.-'`'-.,.-'`'-.,.-'`'-.,.-'`'-.,.-'`'-.,.-'`'-.,.-'`'-.,.-'`'-.,.-' ============================================================================
From this point on, we will work with data structures where values refer to each other.
+- -------------------------------------+ | +- A ------------+ +- B ------------+ | | | : 1 | | : 2 | | | | : ( B) | | : ( A) | | | +------------------------+ +------------------------+ | +--------------------------------------------------------+ The elements of the data structure become mini-structures themselves, containing the value and additional information - references to other elements of the parent structure.
Now you understand what I mean.
/*** ===================================================================== ***\ * * * | RICK ASTLEY'S NEVER GONNA... * * | +-+ * * | +-+ |-| [^] - GIVE YOU UP * * | |^| |-| +-+ [-] - LET YOU DOWN * * | |^| |-| +-+ |*| [/] - RUN AROUND AND DESERT YOU * * | |^| |-| +-+ |\| |*| [\] - MAKE YOU CRY * * | |^| |-| |/| |\| +-+ |*| [.] - SAY GOODBYE * * | |^| |-| |/| |\| |.| |*| [*] - TELL A LIE AND HURT YOU * * | |^| |-| |/| |\| |.| |*| * * +-------------------------------- * ** ** \*** ===================================================================== ***/
/*** ===================================================================== ***\ * * * | RICK ASTLEY'S NEVER GONNA... * * | +-+ * * | +-+ |-| [^] - GIVE YOU UP * * | |^| |-| +-+ [-] - LET YOU DOWN * * | |^| |-| +-+ |*| [/] - RUN AROUND AND DESERT YOU * * | |^| |-| +-+ |\| |*| [\] - MAKE YOU CRY * * | |^| |-| |/| |\| +-+ |*| [.] - SAY GOODBYE * * | |^| |-| |/| |\| |.| |*| [*] - TELL A LIE AND HURT YOU * * | |^| |-| |/| |\| |.| |*| * * +-------------------------------- * ** ** \*** ===================================================================== ***/
Counts
In fact, the graph is not at all what you thought when you saw the ascii graph.
A graph is a structure like this:

We have a lot of “vertices” (A, B, C, D, ...) connected by lines.
These peaks can be represented like this:
Node { value: ..., lines: [(Node), (Node), ...] } And the whole graph will look like this:
Graph { nodes: [ Node {...}, Node {...}, ... ] } Imagine a vertex list with a javascript array. The array is not used for the purpose of specifically organizing vertices, but as a place to store vertices.
class Graph { constructor() { this.nodes = []; } // ... } Let's start adding values to the graph, creating vertices without any lines.
addNode(value) { this.nodes.push({ value: value, lines: [] }); } Now we need a way to search for vertices in the graph. Usually, to speed up the search, another data structure is made on top of the graph.
But in our case, we simply iterate through all the vertices to find the corresponding value. The way is slow, but working.
find(value) { return this.nodes.find(function(node) { return node.value === value; }); } Now we can connect two vertices by drawing a “line” from one to another (approx. Translator: arc of a graph).
addLine(startValue, endValue) { // . var startNode = this.find(startValue); var endNode = this.find(endValue); // , . if (!startNode || !endNode) { throw new Error(' '); } // startNode endNode. startNode.lines.push(endNode); } The resulting graph can be used like this:
var graph = new Graph(); graph.addNode(1); graph.addNode(2); graph.addLine(1, 2); var two = graph.find(1).lines[0]; It seems that too much work has been done for such a small task, but this is a powerful pattern.
It is often used to maintain transparency in complex programs. This is achieved by optimizing the relationships between the data, rather than the operations on the data itself. If you select one vertex in the graph, it is incredibly easy to find related items.
Graphs can represent a lot of things: users and their friends, 800 dependencies in the node_modules folder, even the Internet itself, which is a graph of web pages linked to each other by links.
/*** ===================================================================== ***\ * _______________________ * * ()=(_______________________)=() ,-----------------,_ * * | | ," ", * * | ~ ~~~~~~~~~~~~~ | ,' ,---------------, `, * * | ,----------------------------, ,----------- * * | ~ ~~~~~~~~ | | | * * | `----------------------------' `----------- * * | ~ ~~~~~~~~~~~~~ | `, `----------------' ,' * * | | `, ,' * * |_____________________| `------------------' * * ()=(_______________________)=() * ** ** \*** ===================================================================== ***/
/*** ===================================================================== ***\ * _______________________ * * ()=(_______________________)=() ,-----------------,_ * * | | ," ", * * | ~ ~~~~~~~~~~~~~ | ,' ,---------------, `, * * | ,----------------------------, ,----------- * * | ~ ~~~~~~~~ | | | * * | `----------------------------' `----------- * * | ~ ~~~~~~~~~~~~~ | `, `----------------' ,' * * | | `, ,' * * |_____________________| `------------------' * * ()=(_______________________)=() * ** ** \*** ===================================================================== ***/
Linked lists
Let's now see how a graph-like structure can optimize an ordered list of data.
Linked lists are a common data structure, often used to implement other structures. The advantage of a linked list is the efficiency of adding elements to the beginning, middle and end.
A linked list is inherently similar to a graph: you work with vertices pointing to other vertices. They are arranged in this way:
1 -> 2 -> 3 -> 4 -> 5
1 -> 2 -> 3 -> 4 -> 5
If you imagine this structure in the form of JSON, you get something like this:
{ value: 1, next: { value: 2, next: { value: 3, next: {...} } } } Unlike the graph, a linked list has a single vertex from which the inner chain begins. It is called the "head", the head element, or the first element of the linked list.
We are also going to track the length of the list.
class LinkedList { constructor() { this.head = null; this.length = 0; } // ... } The first thing you need is a way to get the value for this position.
Unlike regular lists, we cannot jump to the desired position. Instead, we must go to it through separate vertices.
get(position) { // , . if (position >= this.length) { throw new Error(' '); } // . var current = this.head; // node.next, // . for (var index = 0; index < position; index++) { current = current.next; } // . return current; } Now we need a way to add vertices to the selected position.
Create an add method that takes a value and a position.
add(value, position) { // , . var node = { value: value, next: null }; // , . // «next» // . if (position === 0) { node.next = this.head; this.head = node; // , // current previous. } else { // . var prev = this.get(position - 1); var current = prev.next; // , «next» // current, // «next» previous — . node.next = current; prev.next = node; } // . this.length++; } The last method we need is remove. Find the top by position and throw it out of the chain.
remove(position) { // , head // . if (position === 0) { this.head = this.head.next; // // , . } else { var prev = this.get(position - 1); prev.next = prev.next.next; } // . this.length--; } ============================================================================ ,.-'`'-.,.-'`'-.,.-'`'-.,.-'`'-.,.-'`'-.,.-'`'-.,.-'`'-.,.-'`'-.,.-'`'-.,.-' ============================================================================
============================================================================ ,.-'`'-.,.-'`'-.,.-'`'-.,.-'`'-.,.-'`'-.,.-'`'-.,.-'`'-.,.-'`'-.,.-'`'-.,.-' ============================================================================
The two remaining data structures belong to the family of "trees".
As in life, there are many different tree data structures.
Notetranslator: well, not-ee, I pass ...
Binary Trees:
AA Tree, AVL Tree, Binary Search Tree, Binary Tree, Cartesian Tree, sibling tree, order statistics tree, Pagoda, ...
B Trees:
B Tree, B + Tree, B * Tree, B Sharp Tree, Dancing Tree, 2-3 Tree, ...
Heaps:
Heap, Binary Heap, Weak Heap, Binomial Heap, Fibonacci Heap, Leonardo Heap, 2-3 Heap, Soft Heap, Pairing Heap, Leftist Heap, Treap,…
Trees:
Trie, Radix Tree, Suffix Tree, Suffix Array, FM-index, B-trie,…
Multi-way Trees:
Ternary Tree, K-ary tree, And-or tree, (( a, b) -tree, Link / Cut Tree, ...
Space Partitioning Trees:
Segment Tree, Interval Tree, Range Tree, Bin, Kd Tree, Quadtree, Octree, Z-Order, UB-Tree, R-Tree, X-Tree, Metric Tree, Cover Tree, ...
Application-Specific Trees:
Abstract Syntax Tree, Parse Tree, Decision Tree, Minimax Tree, ...
What you really did not expect is that you will study dendrology today ... And this is not all trees. Let them not confuse you, most of them do not make sense at all. It was necessary for people to somehow defend their candidate degrees and prove something for this.
Trees are similar to graphs or linked lists, with the difference that they are “unidirectional”. This means that there can be no circular references in them.

If you can walk a circle through the treetops ... well, congratulations, but this is not a tree.
Trees are used in a variety of tasks. They are used to optimize search or sorting. They can better organize the program. They can create a view that is easier to work with.
/*** ===================================================================== ***\ * ccee88oo \ | / * * C8O8O8Q8PoOb o8oo '-.;;;.-, ooooO8O8QOb o8bDbo * * dOB69QO8PdUOpugoO9bD -==;;;;;==-aadOB69QO8PdUOpugoO9bD * * CgggbU8OU qOp qOdoUOdcb .-';;;'-. CgggOU ddqOp qOdoUOdcb * * 6OuU /pu gcoUodpP / | \ jgs ooSec cdac pdadfoof * * \\\// /douUP ' \\\d\\\dp/pddoo * * \\\//// \\ \\//// * * |||/\ \\/// * * |||\/ |||| * * ||||| /||| * ** .............//||||\.......................//|||\\..................... ** \*** ===================================================================== ***/
/*** ===================================================================== ***\ * ccee88oo \ | / * * C8O8O8Q8PoOb o8oo '-.;;;.-, ooooO8O8QOb o8bDbo * * dOB69QO8PdUOpugoO9bD -==;;;;;==-aadOB69QO8PdUOpugoO9bD * * CgggbU8OU qOp qOdoUOdcb .-';;;'-. CgggOU ddqOp qOdoUOdcb * * 6OuU /pu gcoUodpP / | \ jgs ooSec cdac pdadfoof * * \\\// /douUP ' \\\d\\\dp/pddoo * * \\\//// \\ \\//// * * |||/\ \\/// * * |||\/ |||| * * ||||| /||| * ** .............//||||\.......................//|||\\..................... ** \*** ===================================================================== ***/
Trees
Let's start with a simple tree structure. There are no special rules in it, and it looks like this:
Tree { root: { value: 1, children: [{ value: 2, children: [...] }, { value: 3, children: [...] }] } } The tree must begin with a single parent, the "root" of the tree.
class Tree { constructor() { this.root = null; } // ... } We need a way to bypass our tree and call a specific function at each of its vertices.
traverse(callback) { // walk, // . function walk(node) { // callback . callback(node); // walk . node.children.forEach(walk); } // . walk(this.root); } Now we need a way to add vertices to the tree.
add(value, parentValue) { var newNode = { value: value, children: [] }; // , . if (this.root === null) { this.root = newNode; return; } // , // parentValue // . this.traverse(function(node) { if (node.value === parentValue) { node.children.push(newNode); } }); } This is a simple tree, perhaps useful only when the data displayed is similar to it.
However, with additional rules, trees can perform a bunch of different tasks.
/*** ===================================================================== ***\ * 0 0 1 0 1 0 0 1 0 1 1 1 0 1 ,@@@@@@@@@@@@@@, 0 0 1 0 1 0 0 1 0 1 1 1 0 * * 0 1 0 1 0 1 0 1 1 0 1 1 0 @@` '@@ 0 1 0 1 0 1 1 0 1 0 1 0 * * 1 1 0 0 0 1 0 0 1 1 1 0 @@` 8O8PoOb o8o '@@ 0 0 1 0 0 1 0 0 1 1 1 * * 0 0 1 1 0 1 0 1 0 0 0 @@ dOB69QO8PdUgoO9bD @@ 1 0 1 1 0 1 0 1 0 0 * * ===================== @@ CgbU8OU qOp qOdOdcb @@ 0 1 1 0 1 0 1 0 1 0 * * @@ 6OU /pu gcoUpP @@ 1 0 1 1 0 1 0 0 1 1 * * ===================== @@ \\// /doP @@ 0 1 1 0 0 1 0 0 1 0 * * 1 1 0 0 1 1 0 1 1 0 0 @@ \\// @@ 1 0 1 0 0 1 1 0 1 1 * * 0 1 1 0 1 0 1 1 0 1 1 0 @@, ||| ,@@ 0 1 1 0 1 1 0 0 1 0 1 * * 1 0 1 0 1 1 0 0 1 0 0 1 0 @@, //|\ ,@@ 0 1 0 1 0 1 1 0 0 1 1 0 * ** 1 0 1 0 0 1 1 0 1 0 1 0 1 `@@@@@@@@@@@@@@' 0 1 1 1 0 0 1 0 1 0 1 1 ** \*** ===================================================================== ***/
/*** ===================================================================== ***\ * 0 0 1 0 1 0 0 1 0 1 1 1 0 1 ,@@@@@@@@@@@@@@, 0 0 1 0 1 0 0 1 0 1 1 1 0 * * 0 1 0 1 0 1 0 1 1 0 1 1 0 @@` '@@ 0 1 0 1 0 1 1 0 1 0 1 0 * * 1 1 0 0 0 1 0 0 1 1 1 0 @@` 8O8PoOb o8o '@@ 0 0 1 0 0 1 0 0 1 1 1 * * 0 0 1 1 0 1 0 1 0 0 0 @@ dOB69QO8PdUgoO9bD @@ 1 0 1 1 0 1 0 1 0 0 * * ===================== @@ CgbU8OU qOp qOdOdcb @@ 0 1 1 0 1 0 1 0 1 0 * * @@ 6OU /pu gcoUpP @@ 1 0 1 1 0 1 0 0 1 1 * * ===================== @@ \\// /doP @@ 0 1 1 0 0 1 0 0 1 0 * * 1 1 0 0 1 1 0 1 1 0 0 @@ \\// @@ 1 0 1 0 0 1 1 0 1 1 * * 0 1 1 0 1 0 1 1 0 1 1 0 @@, ||| ,@@ 0 1 1 0 1 1 0 0 1 0 1 * * 1 0 1 0 1 1 0 0 1 0 0 1 0 @@, //|\ ,@@ 0 1 0 1 0 1 1 0 0 1 1 0 * ** 1 0 1 0 0 1 1 0 1 0 1 0 1 `@@@@@@@@@@@@@@' 0 1 1 1 0 0 1 0 1 0 1 1 ** \*** ===================================================================== ***/
Binary Search Trees
Binary search trees are a common form of trees. They can effectively read, search, insert and delete values, while maintaining the sorted order.
Imagine that you have a sequence of numbers:
1 2 3 4 5 6 7
1 2 3 4 5 6 7
Let's turn it into a tree, starting from the center.
4 / \ 2 6 / \ / \ 1 3 5 7 -^--^--^--^--^--^--^- 1 2 3 4 5 6 7
4 / \ 2 6 / \ / \ 1 3 5 7 -^--^--^--^--^--^--^- 1 2 3 4 5 6 7
Here is an example of how a binary tree works. Each vertex has two descendants:
- Left - less than the value of the parent node.
- The right one is greater than the value of the parent vertex.
Note: in order for this to work, all values in the tree must be unique.
This makes traversing the tree when searching for a value very effective. For example, try to find the number 5 in our tree.
(4) <--- 5 > 4, . / \ 2 (6) <--- 5 < 6, . / \ / \ 1 3 (5) 7 <--- 5!
(4) <--- 5 > 4, . / \ 2 (6) <--- 5 < 6, . / \ / \ 1 3 (5) 7 <--- 5!
Notice, to get to 5, it took only 3 checks. And if the tree consisted of 1000 elements, the path would be as follows:
500 -> 250 -> 125 -> 62 -> 31 -> 15 -> 7 -> 3 -> 4 -> 5
500 -> 250 -> 125 -> 62 -> 31 -> 15 -> 7 -> 3 -> 4 -> 5
Only 10 checks on 1000 items!
Another important feature of binary search trees is their similarity with linked lists — when adding or removing a value, you only need to update the immediately surrounding elements.
As in the previous section, you first need to set the “root” of the binary search tree.
class BinarySearchTree { constructor() { this.root = null; } // ... } To check if the value is in the tree, you need to search the tree.
contains(value) { // . var current = this.root; // , , . // , null, . while (current) { // value current.value, . if (value > current.value) { current = current.right; // value current.value, . } else if (value < current.value) { current = current.left; // true. } else { return true; } } // , false. return false; } To add an element to the tree, you need to make the same traversal as before, jumping over the left and right vertices, depending on whether they are larger or smaller than the value added.
However, now, when we get to the left or right vertex of null,
we will add a vertex to this position.
add(value) { // . var node = { value: value, left: null, right: null }; // , — . if (this.root === null) { this.root = node; return; } // . var current = this.root; // , // , . while (true) { // value current.value, . if (value > current.value) { // , . if (!current.right) { current.right = node; break; } // . current = current.right; // value current.value, . } else if (value < current.value) { // , . if (!current.left) { current.left = node; break; } // . current = current.left; // , // , . } else { break; } } } /*** ===================================================================== ***\ * .''. * * .''. *''* :_\/_: . * * :_\/_: . .:.*_\/_* : /\ : .'.:.'. * * .''.: /\ : _\(/_ ':'* /\ * : '..'. -=:o:=- * * :_\/_:'.:::. /)\*''* .|.* '.\'/.'_\(/_'.':'.' * * : /\ : ::::: '*_\/_* | | -= o =- /)\ ' * * * '..' ':::' * /\ * |'| .'/.\'. '._____ * * * __*..* | | : |. |' .---"| * * _* .-' '-. | | .--'| || | _| | * * .-'| _.| | || '-__ | | | || | * * |' | |. | || | | | | || | * * _____________| '-' ' "" '-' '-.' '` |____________ * ** jgs~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ** \*** ===================================================================== ***/
/*** ===================================================================== ***\ * .''. * * .''. *''* :_\/_: . * * :_\/_: . .:.*_\/_* : /\ : .'.:.'. * * .''.: /\ : _\(/_ ':'* /\ * : '..'. -=:o:=- * * :_\/_:'.:::. /)\*''* .|.* '.\'/.'_\(/_'.':'.' * * : /\ : ::::: '*_\/_* | | -= o =- /)\ ' * * * '..' ':::' * /\ * |'| .'/.\'. '._____ * * * __*..* | | : |. |' .---"| * * _* .-' '-. | | .--'| || | _| | * * .-'| _.| | || '-__ | | | || | * * |' | |. | || | | | | || | * * _____________| '-' ' "" '-' '-.' '` |____________ * ** jgs~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ** \*** ===================================================================== ***/
the end
I hope you got a good dose of knowledge. If you like it,
put asterisks in the repository and follow me on twitter.
You can also read my other article, “The Super Tiny Compiler” github.com/thejameskyle/the-super-tiny-compiler
// ... module.exports = { List: List, HashTable: HashTable, Stack: Stack, Queue: Queue, Graph: Graph, LinkedList: LinkedList, Tree: Tree, BinarySearchTree: BinarySearchTree }; Also this article can be read on githabe .
Translation: aalexeev , editing: iamo0 , Chaika Chursina.
Source: https://habr.com/ru/post/310794/
All Articles