Automation of measurement of generator harmonic ratio using a digital oscilloscope and MATLAB
In practice, sometimes there is the problem of measuring the harmonic coefficient (Kg) of the signal generator. Such a generator can be both analog and digital. For example, a generator on an operational amplifier, integrated timer (NE555), microcontroller (MK) or programmable logic integrated circuit (FPGA), or digital signal processor (DSP), with output in the form of pulse-width modulation (PWM) or a digital-to-analog signal Converter (DAC). If it is necessary to form a harmonic signal, a low-pass filter (LPF) is installed at the output of the PWM or DAC, which smoothes the stepped waveform and reduces the Kg. In general, measurement of Kg allows you to control the operation of both software algorithms and hardware nodes.
Measurement of Kg is possible with the help of various instruments, for example, in the article “Measurement of the voltage harmonic coefficient of a signal specified in the time domain” , several options are given for measuring this parameter both with traditional measuring instruments and prospective ones. But I want to note that these devices are more specialized than, for example, a digital oscilloscope or a multimeter. Therefore, not every engineer or radio amateur will dare to purchase such a device.
In order to understand how to measure Kg with the help of improvised tools, one should look at its formula. For example, in the article “Nonlinear distortion coefficient” , the physical meaning of this parameter is described in detail. A simple formula that uses only the amplitudes of the signal harmonics. Thus, if we measure the amplitudes of the harmonics of the signal at the generator output, then the solution of the problem of measuring Kg will be reduced to one formula.
Digital oscilloscopes may contain the Fast Fourier Transform (FFT) option. In this case, the oscilloscope switches to FFT measurement mode, and then with the help of markers, the harmonic amplitudes are measured and recorded on a piece of paper.
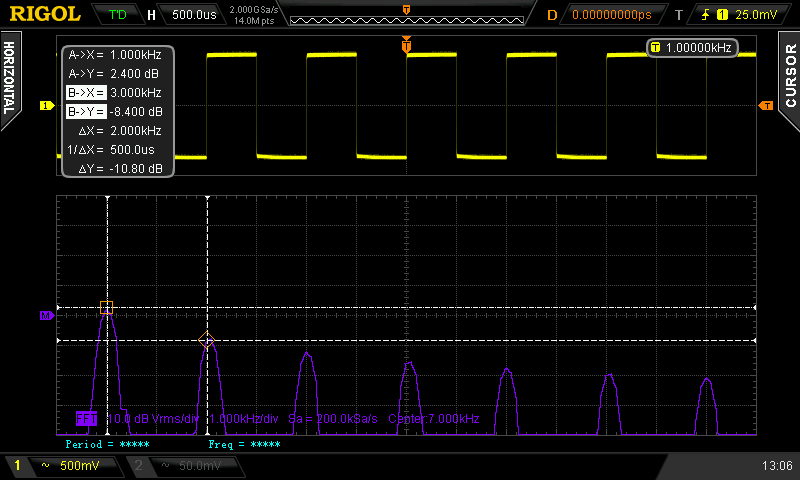
It usually happens, but first of all it is a long time. measurements are made manually. And, secondly, the duration of the signal sampling, and therefore the FFT frequency resolution, as a rule, is significantly limited. It’s another matter if you capture a signal of the desired length using an oscilloscope, for later calculating the spectrum already on your computer.
')
Most digital oscilloscopes with a remote interface, such as USB or Ethernet, can handle capturing a time sample of the signal and transmitting it to a computer. And to calculate the Kg on the spectrum, you can choose Matlab. Moreover, with the Instrument Control Toolbox, remote signal acquisition is performed directly from Matlab.
But before using the method of calculating Kg across the spectrum, one would need to make sure that the oscilloscope is suitable. According to the study, which can be found in the article “Analytic Method for the Compatibility of the Total Harmonic Distribution” , Kg of the meander, as well as signals obtained after filtering the meander with filters of various orders, have certain values that case may be standards. To check you need a generator of rectangular pulses, which must be connected to the oscilloscope.

As well as the corresponding filters that can be implemented programmatically using the Signal Processing Toolbox.

The spectrum of the output signal of the generator of rectangular pulses. Kg = 43.98%
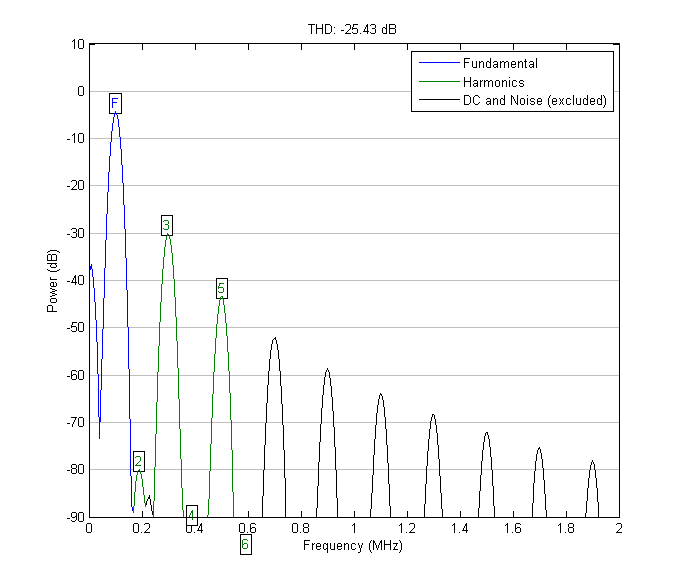
Spectrum at the output of the second-order Butterworth filter. Kg = 5.36%
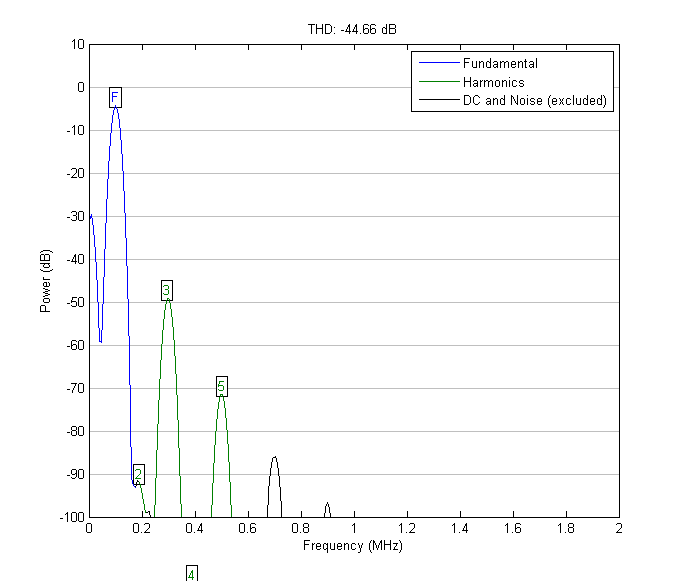
Spectrum at the output of the fourth order Butterworth filter. Kg = 0.59%
A little explanation to the graphs: the logarithmic values of THD in the caps correspond only to the 5 first harmonics, therefore these values differ from the similar ones for which a greater number of harmonics are provided.
It should be noted that Kg at the output of the filters completely coincide with the calculated ones. But Kg for a rectangular signal is less than the calculated one, since the spectrum of a rectangular signal attenuates slowly, and it may take several tens of harmonics to achieve the calculated value - there's nothing to be done.
To automate the measurement of Kg, in addition to the previous script, you may need to support the commands of the tested generator using the Instrument Control Toolbox, but this is only if the device has a remote interface. For example, if commands are implemented as the Command-line Interface (CLI), then everything should be simple.

Actually, this way was measured Kg generator, which was developed on the basis of FPGA, in a module designed to test analog transmission systems. As an example, below are graphs of the spectra and values of Kg directly at the output of the D / A converter (ADC in the figure) and after the link of the type K filter, as well as the necessary script for plotting graphs.
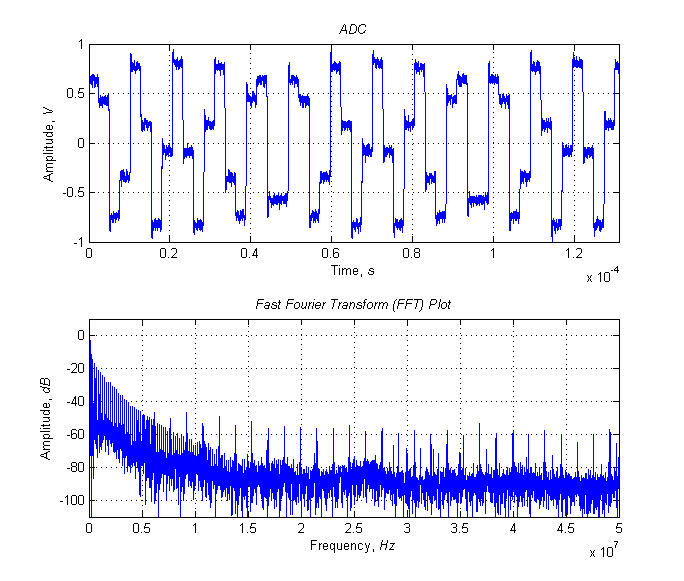
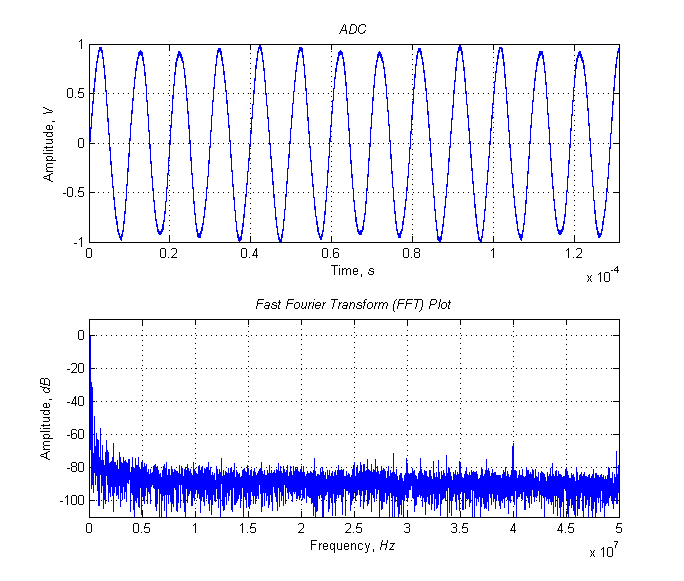
The signal and its spectrum at the output of the DAC, Kg = 28.3%
The signal and its spectrum at the output of a type of filter link, Kg = 2.5%
It should be noted that all this work was carried out only for the sake of estimating the worst Kg value of the maximum generator frequency. In the working frequency range from 200 Hz to 62 kHz, Kg did not exceed 0.34%. For these frequencies, the graphics of the signals and spectra are no longer so interesting.
Thus, using the example of a generator built on a FPGA with a connected DAC and additional filtering of the signal using a low-pass filter of type k, it is shown that measuring Kg at various points in the circuit can be performed using a digital oscilloscope connected to a computer and Matlab. Such a mechanism can significantly reduce the time to assess the quality of the functioning of the device and relieves the engineer from the routine of computing.
Measurement of Kg is possible with the help of various instruments, for example, in the article “Measurement of the voltage harmonic coefficient of a signal specified in the time domain” , several options are given for measuring this parameter both with traditional measuring instruments and prospective ones. But I want to note that these devices are more specialized than, for example, a digital oscilloscope or a multimeter. Therefore, not every engineer or radio amateur will dare to purchase such a device.
In order to understand how to measure Kg with the help of improvised tools, one should look at its formula. For example, in the article “Nonlinear distortion coefficient” , the physical meaning of this parameter is described in detail. A simple formula that uses only the amplitudes of the signal harmonics. Thus, if we measure the amplitudes of the harmonics of the signal at the generator output, then the solution of the problem of measuring Kg will be reduced to one formula.
Digital oscilloscopes may contain the Fast Fourier Transform (FFT) option. In this case, the oscilloscope switches to FFT measurement mode, and then with the help of markers, the harmonic amplitudes are measured and recorded on a piece of paper.

It usually happens, but first of all it is a long time. measurements are made manually. And, secondly, the duration of the signal sampling, and therefore the FFT frequency resolution, as a rule, is significantly limited. It’s another matter if you capture a signal of the desired length using an oscilloscope, for later calculating the spectrum already on your computer.
')
Most digital oscilloscopes with a remote interface, such as USB or Ethernet, can handle capturing a time sample of the signal and transmitting it to a computer. And to calculate the Kg on the spectrum, you can choose Matlab. Moreover, with the Instrument Control Toolbox, remote signal acquisition is performed directly from Matlab.
function [osc_data,fs] = osc_capture_ds2202() ds2000 = visa('ni','USB0::0x1AB1::0x04B0::DS2A142900939::INSTR'); % Create VISA object. ds2000.InputBufferSize = 2e6; fopen(ds2000); fprintf(ds2000,':CHAN1:BWLimit 20M'); % Set BandWidth Limit to 20MHz. fprintf(ds2000,':ACQ:MDEPth 140000'); % Set Memory Depth from several typical values. fs = str2double(query(ds2000,':ACQ:SRATe?')); % Get Sample Rate. %% Setup Waveform fprintf(ds2000,':STOP'); % Stop oscilloscope. fprintf(ds2000,':WAV:SOURce CHAN1'); fprintf(ds2000,':WAV:MODE RAW'); fprintf(ds2000,':WAVeform:FORMat ASCII'); fprintf(ds2000,':WAV:POINts 131072'); % Number of points that must be less than MDEPth. fprintf(ds2000,':WAV:RESet'); fprintf(ds2000,':WAV:BEGin'); pause(5); % Wait the end of the acquisition. %% Get Waveform while true status = query(ds2000,':WAV:STATus?'); pause(1); % Not neccesary, but... [state,rem] = strtok(status,','); len = strtok(sscanf(rem,'%s'),','); if eq(len,'0') break; end if eq(state(1),'I') osc_data = cell2mat(textscan(query(ds2000,':WAV:DATA?'),'%f','delimiter',',')); break; else osc_data = cell2mat(textscan(query(ds2000,':WAV:DATA?'),'%f','delimiter',',')); end end fprintf(ds2000,':WAV:END'); fprintf(ds2000,':RUN'); % Run the oscilloscope. %% Delete instrument object fclose(ds2000); delete(ds2000); clear ds2000; But before using the method of calculating Kg across the spectrum, one would need to make sure that the oscilloscope is suitable. According to the study, which can be found in the article “Analytic Method for the Compatibility of the Total Harmonic Distribution” , Kg of the meander, as well as signals obtained after filtering the meander with filters of various orders, have certain values that case may be standards. To check you need a generator of rectangular pulses, which must be connected to the oscilloscope.

As well as the corresponding filters that can be implemented programmatically using the Signal Processing Toolbox.
clear all clc %% Signal Acquisition [s,fs] = osc_capture_ds2202(); % s - signal, fs - sample frequency. %% Setup parameters number_of_harmonics = 11; % Number of harmonics (including the fundamenal)... % to use in the THD calculation. L = length(s); % Length of the signal for FFT computing. It is used only for plot. T = 1/fs; t = (0:L-1)*T; s_ac = s-mean(s); % Remove DC level. It is not neccesary for thd function. s_ac = s_ac/max(abs(s_ac)); % Normalize signal. As above for thd. %% Estimate the THD of the signal [thd_dBc,harmpow,harmfreq] = thd(s_ac,fs,number_of_harmonics); thd_perc = 10^(thd_dBc/20)*100 % Convert dB to Percents and display result. figure(2); thd(s_ac,fs); % Plot the Spectrum of the signal. %% Apply Butterworth filter to signal and estimate THD for filtered signal [lpFilter_b_II, lpFilter_a_II] = butter(2,2*harmfreq(1)/fs,'low'); % Design B-II filter. filtII_s_ac = filter(lpFilter_b_II, lpFilter_a_II, s_ac); % Apply B-II filter to signal. thd_perc_BII = 10^(thd(filtII_s_ac,fs,number_of_harmonics)/20)*100 % Convert dB to Percents and display result. figure(3); thd(filtII_s_ac,fs); % Plot the Spectrum of the B-II filter. [lpFilter_b_IV, lpFilter_a_IV] = butter(4,2*harmfreq(1)/fs,'low'); % Design B-IV filter. filtIV_s_ac = filter(lpFilter_b_IV, lpFilter_a_IV, s_ac); % Apply B-IV filter to signal. thd_perc_BIV = 10^(thd(filtIV_s_ac,fs,number_of_harmonics)/20)*100 % Convert dB to Percents and display result. figure(4); thd(filtIV_s_ac,fs); % Plot the Spectrum of the B-IV filter. 
The spectrum of the output signal of the generator of rectangular pulses. Kg = 43.98%

Spectrum at the output of the second-order Butterworth filter. Kg = 5.36%

Spectrum at the output of the fourth order Butterworth filter. Kg = 0.59%
A little explanation to the graphs: the logarithmic values of THD in the caps correspond only to the 5 first harmonics, therefore these values differ from the similar ones for which a greater number of harmonics are provided.
It should be noted that Kg at the output of the filters completely coincide with the calculated ones. But Kg for a rectangular signal is less than the calculated one, since the spectrum of a rectangular signal attenuates slowly, and it may take several tens of harmonics to achieve the calculated value - there's nothing to be done.
To automate the measurement of Kg, in addition to the previous script, you may need to support the commands of the tested generator using the Instrument Control Toolbox, but this is only if the device has a remote interface. For example, if commands are implemented as the Command-line Interface (CLI), then everything should be simple.
[qty,b5_comport_list,~,b5] = b5_open_test; % Search connected devices. if qty b5.Port = b5_comport_list{1}; % Assign port to first device. fopen(b5); disp(b5_command(b5,'versions',.1)); % Display Versions of MCU and FPGA. disp(b5_command(b5,'sn',.1)); % Display Serial Number. b5_command(b5,'outrfreq 101050',.1); % Set output frequency. b5_command(b5,'outrlvl 0',.1); % Set output level. b5_command(b5,'outimp 600',.1); % Set output impedance. b5_command(b5,'outpath output',.1); % Connect generator to output connector. fclose(b5); % Close port. delete(b5); % Clear buffer. clear b5 % Remove var from memory. else disp('b5-vf is not connected'); delete(b5); % Clear buffer. clear b5 % Remove var from memory. end 
Actually, this way was measured Kg generator, which was developed on the basis of FPGA, in a module designed to test analog transmission systems. As an example, below are graphs of the spectra and values of Kg directly at the output of the D / A converter (ADC in the figure) and after the link of the type K filter, as well as the necessary script for plotting graphs.
%% Window win = tukeywin(length(s_ac),1); % Generate window. % win = 1; % Disable window. s_ac_win = s_ac.*win; % Apply the window. %% FFT nfft = 2^nextpow2(L); %% FFT length fft_s_ac_win = fft(s_ac_win,nfft)/L; f = fs/2*linspace(0,1,nfft/2+1); win_scale = 1/mean(win); %% Normalization the result fft_s_ac_win_lin = 2*win_scale*abs(fft_s_ac_win(1:nfft/2+1)); fft_s_ac_win_log = 20*log10(fft_s_ac_win_lin); %% Fig 1 figure(1); subplot(2,1,1), plot(t,s_ac), axis([0 max(t) -max(abs(s_ac)) max(abs(s_ac))]), grid on; title('\itADC','fontsize',10); xlabel('Time, \its','fontsize',10), ylabel('Amplitude, \itV','fontsize',10); subplot(2,1,2), plot(f,fft_s_ac_win_log), axis([0 fs/2 -110 10]), grid on; title('\itFast Fourier Transform (FFT) Plot','fontsize',10); xlabel('Frequency, \itHz','fontsize',10), ylabel('Amplitude, \itdB','fontsize',10); 
The signal and its spectrum at the output of the DAC, Kg = 28.3%

The signal and its spectrum at the output of a type of filter link, Kg = 2.5%
It should be noted that all this work was carried out only for the sake of estimating the worst Kg value of the maximum generator frequency. In the working frequency range from 200 Hz to 62 kHz, Kg did not exceed 0.34%. For these frequencies, the graphics of the signals and spectra are no longer so interesting.
Thus, using the example of a generator built on a FPGA with a connected DAC and additional filtering of the signal using a low-pass filter of type k, it is shown that measuring Kg at various points in the circuit can be performed using a digital oscilloscope connected to a computer and Matlab. Such a mechanism can significantly reduce the time to assess the quality of the functioning of the device and relieves the engineer from the routine of computing.
Source: https://habr.com/ru/post/310582/
All Articles