Correct polyhedra. Part 1.1 The Schläfli Symbol
 Habrahabr, dear colleagues! When I look at the honeycomb, I think not about the bees, but about the Schläfli Symbol. After reading this article, you will not be able to look at the world in the old way, you will understand that there is a direct connection between cells and regular polyhedra.
Habrahabr, dear colleagues! When I look at the honeycomb, I think not about the bees, but about the Schläfli Symbol. After reading this article, you will not be able to look at the world in the old way, you will understand that there is a direct connection between cells and regular polyhedra.From the experience of explaining to friends the derivation of regular polyhedra in four-dimensional space and spaces of higher dimensions, it turns out that few people know what Schläfli's symbol is, so I decided to devote to this a separate article with pictures, without analytic calculations, which are made in my other, neighboring articles , with direct derivation of polyhedra. In this article, my task is to give a figurative and intuitive understanding of the term Schläfli's symbol, therefore I will not spend your attention on the strict definitions and wording that can be read in Wikipedia. The concept of the Symbol Schläfli will be mastered from the easy to the difficult. The simplest on the plane.
How does the triangle work? Answer: from three identical sides. Schläfli Symbol {3}
How does the square? Answer: from four identical sides. Schläfli Symbol {4}
How is the correct devagon? Answer: from nine identical sides. Schläfli symbol {9} See picture:

True basic questions? Let's in the opposite direction - what is the name and the structure of a regular polygon defined by its Schläfli Symbol {10}?
Answer
A regular decagon, it consists of ten identical sides.
So, the simplest thing after all is the Schlefli Symbol for two-dimensional space. The designation {p1}, where p1 is an integer greater than or equal to 3, simply because there are no two-angles, in the usual sense. The number p1 at the same time shows the number of edges of a regular polygon (two-dimensional polyhedron), see the figure above.
It seems that everything is obvious, {3} is a regular triangle, {4} is a square, {9} is a regular nonagon, and so on.
')
On the plane, this is the first step in understanding the Schläfli Symbol, I hope the link between the symbol and the structure of the polygon is clear. Let's make the second step on the way to the difficult one - for three-dimensional regular polyhedrons, the answers to the questions about the structure of these polyhedrons are also given by the Schläfli Symbol. Those. The Schläfli symbol generalizes the concept of the number of sides of a regular polygon to regular polyhedrons.
Namely: How does the Cube work?
Answer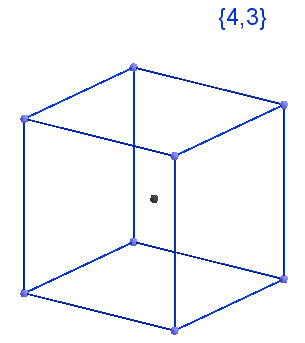 The cube is {4, 3}, it is his Schläfli Symbol, which means that it consists of 4 triangles that converge 3 at the top. Figure on the left.
The cube is {4, 3}, it is his Schläfli Symbol, which means that it consists of 4 triangles that converge 3 at the top. Figure on the left.
Those. a cube is obtained by connecting 3 squares {4}, at each vertex. Gluing in one of the vertices is shown in the video.
 The cube is {4, 3}, it is his Schläfli Symbol, which means that it consists of 4 triangles that converge 3 at the top. Figure on the left.
The cube is {4, 3}, it is his Schläfli Symbol, which means that it consists of 4 triangles that converge 3 at the top. Figure on the left.Those. a cube is obtained by connecting 3 squares {4}, at each vertex. Gluing in one of the vertices is shown in the video.
Links to programs
A free program in which an animation is drawn is called GeoGebra, you can download it here: www.geogebra.org/download
The video was recorded under the Ubuntu operating system, the recording program is called recordmydesktop.
The video was recorded under the Ubuntu operating system, the recording program is called recordmydesktop.
Similarly, the Schläfli symbols define the remaining four regular polyhedra.
How is the Octahedron?
Answer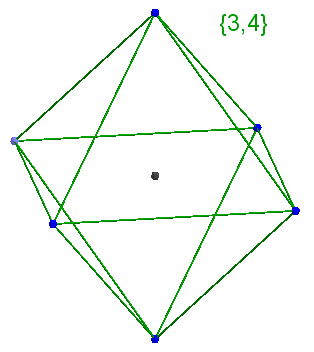 {3, 4} - Schläfli symbol, which means that the octahedron consists of 3-squares that converge 4 at the top.
{3, 4} - Schläfli symbol, which means that the octahedron consists of 3-squares that converge 4 at the top.
 {3, 4} - Schläfli symbol, which means that the octahedron consists of 3-squares that converge 4 at the top.
{3, 4} - Schläfli symbol, which means that the octahedron consists of 3-squares that converge 4 at the top.How does the icosahedron work?
Answer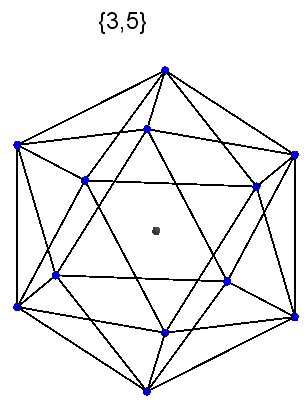 {3, 5} - Schläfli Symbol, which means that the Icosahedron consists of 3-gons, converging 5 at the top.
{3, 5} - Schläfli Symbol, which means that the Icosahedron consists of 3-gons, converging 5 at the top.
 {3, 5} - Schläfli Symbol, which means that the Icosahedron consists of 3-gons, converging 5 at the top.
{3, 5} - Schläfli Symbol, which means that the Icosahedron consists of 3-gons, converging 5 at the top.Let's in the opposite direction, what figure does the Schlefli Symbol {3, 3} mean, 3-corners converged 3 at the top?
Answer tetrahedron
tetrahedron
 tetrahedron
tetrahedronWhat shape does the Schläfli Symbol {5, 3} mean, three pentagons at the vertex?
Answer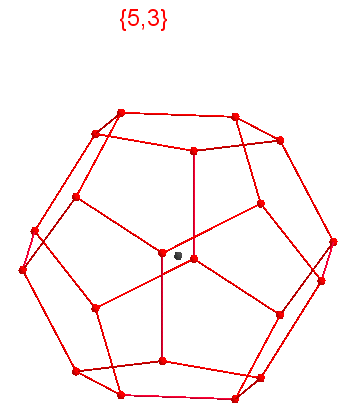 Dodecahedron
Dodecahedron
 Dodecahedron
DodecahedronThis is the whole meaning of the Schläfli Symbol in three dimensions, for regular polyhedra. In trimesters, we can touch the right polyhedra, show clearly in the picture, in the video, so our usual trimerie is the best space in which you can understand the essence of the Schläfli Symbol well. And when this line will be overcome, then we will deepen, be bothered.
Initially, I had a great desire to print the correct polyhedra on a 3D printer, so I started to master the free program OpenSCAD on the recommendation of one article on Habré .
Links
You can download OpenSCAD here. Primary knowledge and skills for working in the program can be obtained in the same article on Habré ; they couldn’t put a plus in their karma, for the company
At the same time, it was unexpectedly possible to write an algorithm that, using the Schläfli Symbol (i.e., using the two input parameters p1, p2), builds the corresponding regular polyhedron. It's great that we managed to make such a unified algorithm, it is an independent small, interesting result, while the listing fits on one screen, only one if statement and, most importantly, you can very clearly demonstrate the meaning of the Schläfli Symbol. This algorithm was able to show that the structure of a regular polyhedron in three dimensions depends only on two parameters {p1, p2} we watch the video below. When watching a video, you need to complete the task, you need to calculate how many edges of two-dimensional faces of polyhedra and how many two-dimensional faces converge at the top. If you complete this task, the riddle of the Schläfli Symbol will be revealed to you forever.
Sources of the algorithm with comments
// {p1, p2} /* {3,3} - {3,4} - {4,3} - {3,5} - {5,3} - */ p1=5; // p2=3; // // accuracy=100; // sphere_radius = 10; // edge_angle_half = 90-asin(cos(180/p1)/sin(180/p2)); // edge_length_half = sphere_radius*sin(edge_angle_half); // rb_face = edge_length_half/sin(180/p1); // rs_face = edge_length_half/tan(180/p1); // angle_up = 180-2*asin(cos(180/p2)/sin(180/p1)); // angle_up1 = asin(sin(90-asin(cos(180/p1)/sin(180/p2)))/sin(180/p1)); // rs_polytop=sphere_radius*cos(angle_up1); // ch=rs_polytop; //ch=1; // //difference() { rotate([0, angle_up1, 0]){// , , 3D union(){ ten_edge();// if (!(p1==3 && p2==3)) rotate([0, 180, 0]) ten_edge();// , , , } } //sphere(r=rs_polytop-0.3, $fn=accuracy);// , 3D //} module ten_edge(){ translate([0, 0, -sphere_radius]) for (i=[0:1:p2]) rotate([0, -angle_up1, i*360/p2])/* , p2 Oz, 1, */ translate([rb_face, 0, 0])/* , */ rotate([0, 0, (180/p1)*(1-p1+2*floor(p1/2))])/* */{ union(){ rotate([0, 0, 180/p1]) cylinder(h=ch, r1=rb_face, /*r2=rb_face-0.75*/ r2=0, center=false, $fn=p1);// , , translate([rs_face, 0, 0]) rotate([0, -angle_up, 0]) translate([rs_face, 0, 0]) rotate([0, 0, 180+180/p1]) cylinder(h=ch, r1=rb_face, /*r2=rb_face-0.75*/ r2=0, center=false, $fn=p1);// } } } I recommend to download OpenSCAD to insert the source code of the algorithm there and experiment with polyhedra myself. The most inquisitive will want to insert there any other numbers. I remind you who have forgotten that there are only five regular polyhedra in trimesters, so the video shows all possible options, for trimery, there are no others.
The next step of the challenge is to answer what the Schläfli Symbols mean {4, 4}, {6, 3}, {3, 6}?
Hint: these are not polyhedrons; they are other figures that are visually known to everyone.
Answer: {4, 4}
{4, 4} is a piece in a box, quadrangles, converging 4 pieces at the top. Indeed, the square cells, and at the vertices of all squares converges on 4 of the same squares. This partition of the Euclidean plane into squares, it can be continued to infinity.
Now you can answer what is {6, 3}?
Answer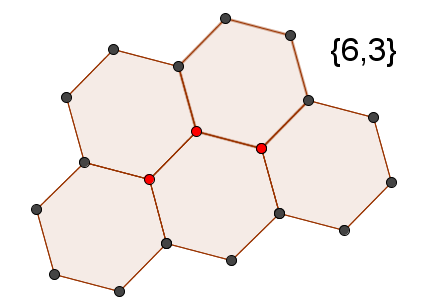 Honeycomb
Honeycomb
 Honeycomb
HoneycombWhat is {3, 6}?
Answer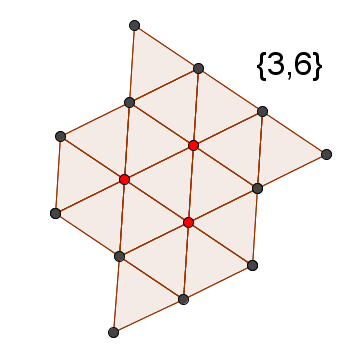 The points in red are shown in which all 6 converged triangles are shown, in the remaining vertices you need to continue drawing, but you can continue indefinitely, so you had to stop at something.
The points in red are shown in which all 6 converged triangles are shown, in the remaining vertices you need to continue drawing, but you can continue indefinitely, so you had to stop at something.
 The points in red are shown in which all 6 converged triangles are shown, in the remaining vertices you need to continue drawing, but you can continue indefinitely, so you had to stop at something.
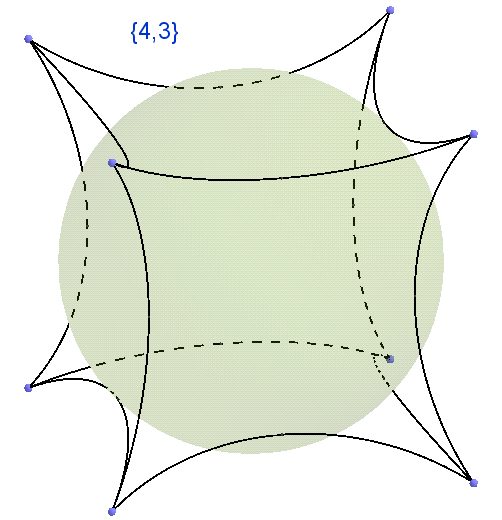
The points in red are shown in which all 6 converged triangles are shown, in the remaining vertices you need to continue drawing, but you can continue indefinitely, so you had to stop at something.Well, all three existing DIVISIONS (with an emphasis on the word DIVISION) on the Euclidean plane we looked at, others not, it was shown in the article. Now when you keep a notebook in a cage, these are not simple cells, it is {4,4} splitting the Euclidean plane ; when you look at the honeycomb, remember that it is {6.3}. I am sure {3,3} also surely catches the eye. We smoothly from the polyhedra, which are each denoted by their Schläfli Symbol, moved on to the tilings of the Euclidean plane, which are also denoted by the Schläfli Symbol. Now the next step (generalizations) of difficulty in understanding the Symbol of Schläfli is that it sets the BINDING sphere. So {3, 4} is, on the one hand, an octahedron, on the other hand, it is a partition of a sphere into regular spherical triangles converging 4 pieces at the top; {4, 3} - on the one hand a cube, on the other hand it is a partition of the sphere into regular spherical quadrilaterals, converging 3 pieces at the top. More clearly this is shown in the video. Count the number of two-dimensional faces and how many such faces converge at the vertices.
Of the entire class of objects, when bending the edges shown in the video, two are most interesting:
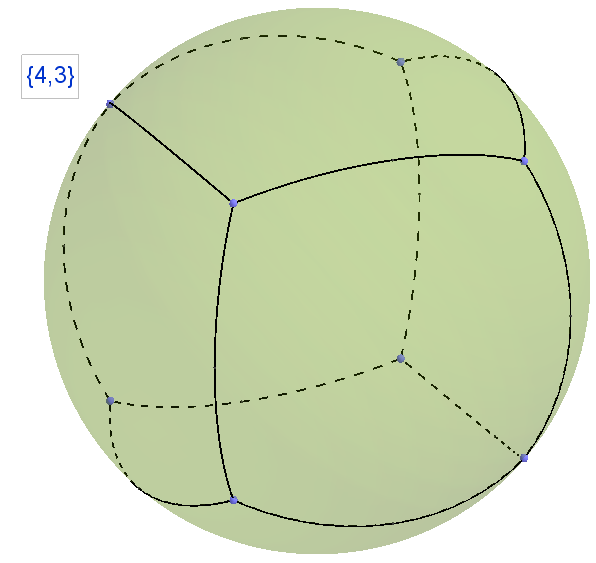
Fig. 33 Splitting a two-dimensional sphere into squares, three pieces at each vertex, symbol {4.3}
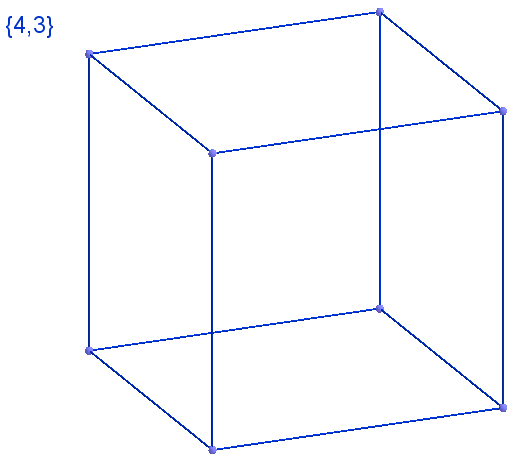
Fig. 34 Correct polyhedron, cube, symbol {4,3}
Further video on the bending of the edges of the octahedron, {3,4}
Of the entire class of objects, when bending the edges shown in the video, two are also the most interesting:
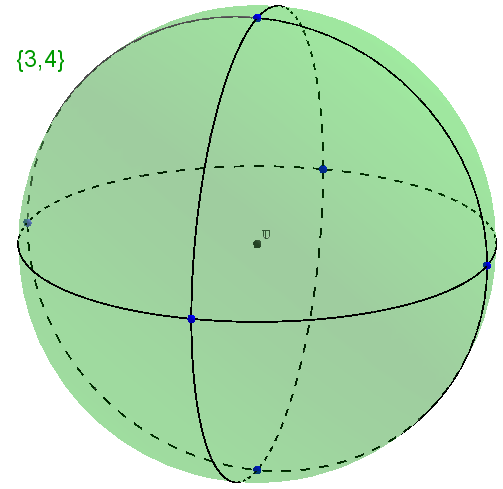
Fig. 35 Splitting a two-dimensional sphere into triangles, four pieces at each vertex, symbol {3,4}

Fig. 36 Correct polyhedron, octahedron, symbol too {3, 4}
We kind of inflate a polyhedron (we place it on a sphere), while flat faces also swell, the corners at the vertices and the dihedral angles at the edges increase. Either we blow it away (we place it in Lobachevsky space), the flat faces also deflate, the corners at the vertices and the dihedral angles at the edges decrease.
Those. Schläfli’s symbols define a whole class of shapes, since any bending of ribs without breaks does not change the Schläfli Symbol; this is shown in the video by the fact that the Schläfli Symbol designation is displayed throughout the entire recording, while the edges are bent, and the Schläfli Symbol remains the same. The video shows special bends in which all the corners of the figures change simultaneously and equally.
Of the entire class of figures given by the Schläfli Symbol, we are primarily interested in three particular cases:
- when the Schläfli Symbol sets the correct polyhedron;
- when the Schläfli Symbol specifies a partition of the sphere;
- when the Schläfli Symbol specifies a partition of Lobachevsky space.
These and related cases are shown in the video above. The video shows only the cube and the octahedron, but the situation is exactly the same with the other three regular polyhedra {3,3} -Tetrahedron, {3,5} -Icosahedron, {5,3} -Dodecahedron. From this point on, when we started talking about the splitting of the sphere, we must be very careful about the dimension of the space in which we work. The fact is that the surface of a sphere is two-dimensional, and polyhedra are three-dimensional, but the divisions of the sphere and the polyhedron corresponding to the partition are denoted by the same Schläfli Symbol. For example, as it was already said, {3, 4} is an octahedron in three-dimensional Euclidean space, at the same time {3, 4} are partitions of a two-dimensional surface of a sphere into spherical triangles, i.e. splitting of two-dimensional spherical space. What is a spherical triangle is intuitive, but who wants to clarify on this issue can be found in the article . Thus, when we speak of the Schläfli Symbol, which defines the partitioning of the surface of the Sphere, we are simultaneously in two neighboring dimensions of the spaces. At the same time, the Schläfli Symbol {3, 6} defines a partition of the Euclidean plane, i.e. splitting of the Euclidean plane is also here nearby.
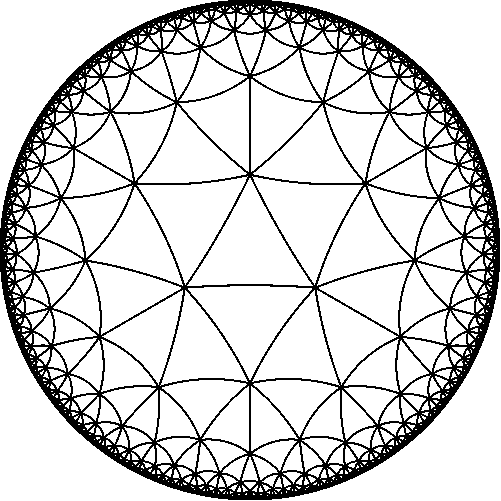
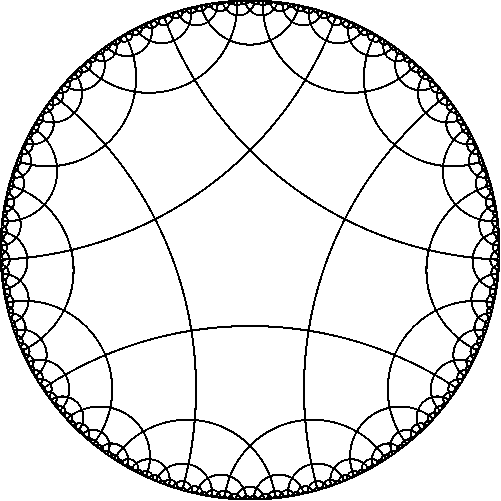
Well, the completeness of the picture and the understanding of the meaning of the Symbol of Schlefli comes when we proceed to the next step of difficulty (generalization) and begin to talk about DIVIDING the Lobachevsky plane. Do not worry, we have enough basic, intuitive skills of working with the Lobachevsky plane, such skills are given in the same article , where about the sphere, there are also pictures of these tilings of the Lobachevsky plane. This is not an extreme step of complication, but completeness comes because the spherical, Euclidean and Lobachevsky spaces are all three spaces of constant curvature, there are no other such (with constant curvature) spaces. So the Schläfli Symbol {3, 6} specifies the partition of the Euclidean plane, and {3, 7} defines the partition of the Lobachevsky plane. {3, 8}, {3, 9}, etc. {3, p2} where p2> = 7 - all these are tilings of the Lobachevsky plane into regular triangles. There are an infinite set of such partitions (a countable number). For example, here’s two pictures of the {3,7} and {5,4} partitions, make sure that in the first case 7 triangles converge at each vertex, and 4 pentagons in the second vertex.
To work with Spherical space and Lobachevsky space, it is enough to imagine that when an object is placed on the Sphere, it “inflates”, and when placed in Lobachevsky space, it “deflates”.
The next step of comprehension (generalization) in understanding the Schläfli Symbol is the transition to the 4-dimensional Euclidean space, which according to the Schläfli Symbol is connected with partitions of the 3-dimensional Spherical space, as was similar in the dimension below, as we have already said {4,3} - the cube and the division of the sphere into spherical squares. Here it is already more difficult to draw pictures, turn on the imagination, but I will try to draw something.
The first thing that needs to be understood is the transition from the Schlefly Symbol {p1, p2} to the Schlefly Symbol to a dimension above {p1, p2, p3}. We show the transition from {4,3} to {4,3,4}. So in the three-dimensional {4, 3} quadrangles (flat faces), they are glued together along the edges (one-dimensional faces) and 3 pieces converge at the vertex (the top is a zero-dimensional face). Similarly for the Schläfli Symbol {p1, p2, p3}, for example {4, 3, 4} is the same as {{4, 3}, 4}, which means that {4.3} cubes (three-dimensional faces) , stick together among themselves on squares (two-dimensional edges), and converge in edges (one-dimensional edges) on 4 pieces in each edge. So what is {4, 3, 4}? Cubes have agreed on 4 pieces in each edge, what is it? Think before you open the answer.
Answer This is a partition of 3-dimensional Euclidean space into cubes. Everything is simple, it is a well-known object. Notice that exactly 4 cubes converged in the edges, this is shown on the example of the edge highlighted in red. The number p3 in the symbol {p1, p2, p3} = {4, 3, 4} means that the edges converge in p3 = 4 pieces of polyhedrons, and the meaning of the numbers {p1, p2} remains the same, which means the types of polyhedra that converge in ribs.
This is a partition of 3-dimensional Euclidean space into cubes. Everything is simple, it is a well-known object. Notice that exactly 4 cubes converged in the edges, this is shown on the example of the edge highlighted in red. The number p3 in the symbol {p1, p2, p3} = {4, 3, 4} means that the edges converge in p3 = 4 pieces of polyhedrons, and the meaning of the numbers {p1, p2} remains the same, which means the types of polyhedra that converge in ribs.
 This is a partition of 3-dimensional Euclidean space into cubes. Everything is simple, it is a well-known object. Notice that exactly 4 cubes converged in the edges, this is shown on the example of the edge highlighted in red. The number p3 in the symbol {p1, p2, p3} = {4, 3, 4} means that the edges converge in p3 = 4 pieces of polyhedrons, and the meaning of the numbers {p1, p2} remains the same, which means the types of polyhedra that converge in ribs.
This is a partition of 3-dimensional Euclidean space into cubes. Everything is simple, it is a well-known object. Notice that exactly 4 cubes converged in the edges, this is shown on the example of the edge highlighted in red. The number p3 in the symbol {p1, p2, p3} = {4, 3, 4} means that the edges converge in p3 = 4 pieces of polyhedrons, and the meaning of the numbers {p1, p2} remains the same, which means the types of polyhedra that converge in ribs.So, the next step of the complication is to consider the meaning of the symbol {4, 3, 3}. There was a partition of the 3-dimensional Euclidean space into cubes {4,3,4}, but let's remove one cube from the edge, we get {4,3,3}, what is it in Euclidean?
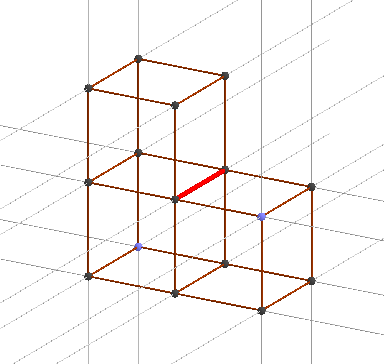 It turned out it is not clear that this is not a split, since the flat faces of the cubes are not glued to each other. What you need to do so they stuck? You need to inflate these cubes like balls and inflate as long as the two-dimensional faces of the cubes match, this is where we will glue them together. Inflate is a figurative expression, in mathematics it is called to place cubes (and they are three-dimensional) on a sphere, to make cubes spherical, similar to how we looked at spherical triangles on a two-dimensional sphere, only now cubes are three-dimensional, which means we put them on a three-dimensional sphere. The sphere itself is placed in four-dimensional Euclidean space, but its surface is three-dimensional. Those. {4,3,3} splits a three-dimensional sphere into cubes converging 3 pieces in an edge.
It turned out it is not clear that this is not a split, since the flat faces of the cubes are not glued to each other. What you need to do so they stuck? You need to inflate these cubes like balls and inflate as long as the two-dimensional faces of the cubes match, this is where we will glue them together. Inflate is a figurative expression, in mathematics it is called to place cubes (and they are three-dimensional) on a sphere, to make cubes spherical, similar to how we looked at spherical triangles on a two-dimensional sphere, only now cubes are three-dimensional, which means we put them on a three-dimensional sphere. The sphere itself is placed in four-dimensional Euclidean space, but its surface is three-dimensional. Those. {4,3,3} splits a three-dimensional sphere into cubes converging 3 pieces in an edge. 
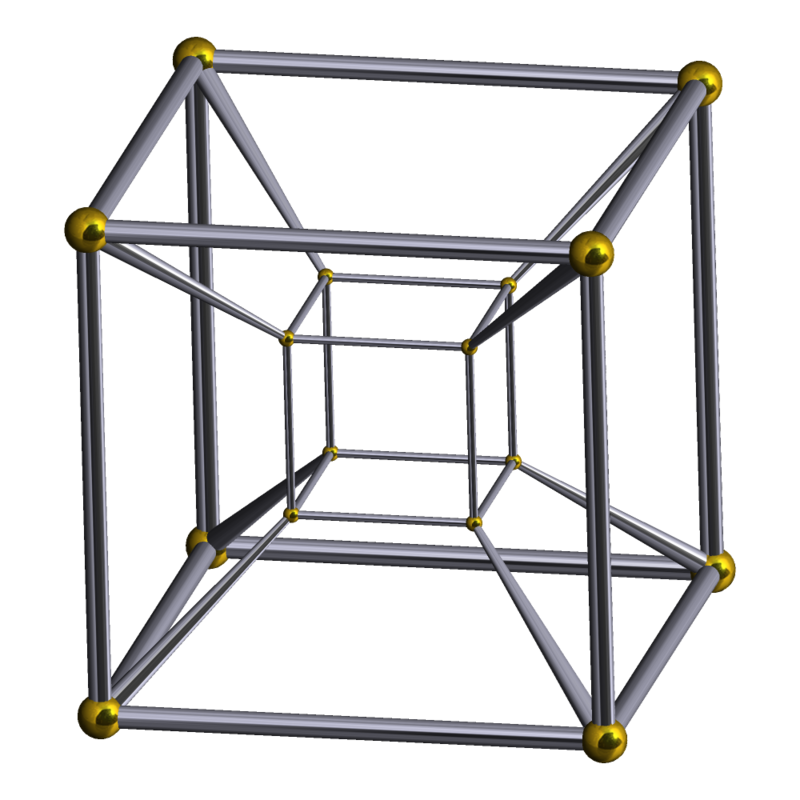 It is difficult to draw fourfolds on a plane, but people have already learned how to do this, pay attention to how the edges are bent (left), this is because the object {4,3,3} on the sphere, in this case means splitting the three-dimensional sphere. But after all, we already know that partitions of a sphere correspond to polyhedra one dimension higher than the surface of the sphere, which means {4,3,3} is a regular polyhedron in 4 dimensional Euclidean space (on the right), this is a Tesseract, a four-dimensional cube. Almost the same, only the edges of the straight steel, in the same way as we were bending the edges of three-dimensional polyhedra, we can also bend the edges of four-dimensional polyhedra, to obtain the desired result.
It is difficult to draw fourfolds on a plane, but people have already learned how to do this, pay attention to how the edges are bent (left), this is because the object {4,3,3} on the sphere, in this case means splitting the three-dimensional sphere. But after all, we already know that partitions of a sphere correspond to polyhedra one dimension higher than the surface of the sphere, which means {4,3,3} is a regular polyhedron in 4 dimensional Euclidean space (on the right), this is a Tesseract, a four-dimensional cube. Almost the same, only the edges of the straight steel, in the same way as we were bending the edges of three-dimensional polyhedra, we can also bend the edges of four-dimensional polyhedra, to obtain the desired result.
Let's return once more to the well-known division of the three-dimensional Euclidean space into cubes converging by 4 in the edge {4,3,4}. Above, we threw one cube to {4,3,3} and inflated the remaining 3 cubes until the flat faces of the cubes coincide. And what if you start to blow away the existing 4 cubes, separating two adjacent cubes in one place along flat faces? Then there will be a gap between these faces. But you can continue to blow it away, until another similar “deflated” cube fits into this gap, then we get {4,3,5} - a partition of the 3-dimensional Lobachevsky space into cubes. When we blew the cubes, strictly speaking, we placed them in Lobachevsky space.
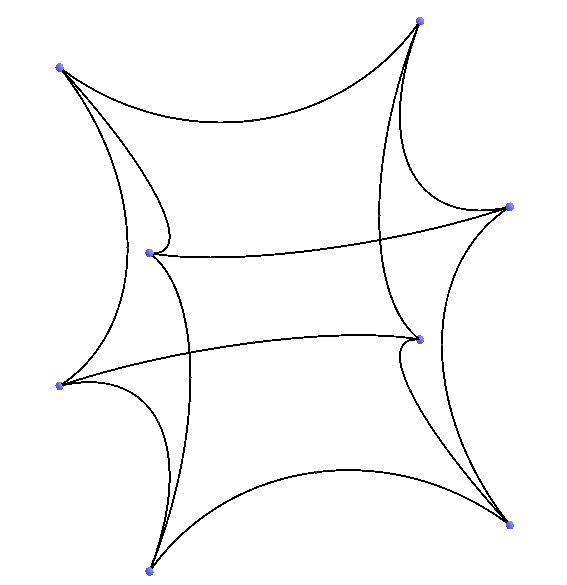
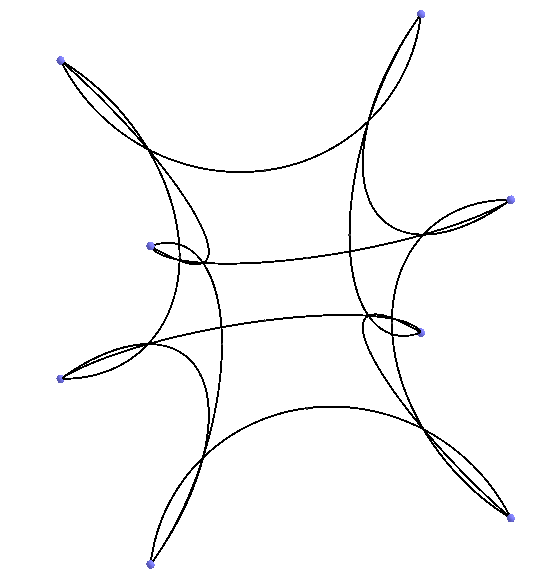 We have already seen blown-up cubes in one of the videos above (picture on the left). So, by blowing away, we get tilings of the three-dimensional Lobachevsky space, into regular polyhedra. Only you need to be careful, you can not blow cubes too long, otherwise self-intersection of edges is formed (figure on the right). It is in the figure that our self-intersections have formed, and in the sense of the 3-dimensional Lobachevsky space, this means that the vertices of the cube have gone beyond the absolute. Thus, six cubes in the edge are denoted by the Schlefli Symbol {4,3,6} and already at this partition of the 3-dimensional Lobachevsky vertex space are located directly on the absolute. The {4,3,7} vertices already go beyond the absolute, these Schlefli Symbols also show partitions of the 3-dimensional Lobachevsky space, but strictly speaking, not into regular polyhedra, but into something else, here you can already figure out how to call these objects and agree about their name.
We have already seen blown-up cubes in one of the videos above (picture on the left). So, by blowing away, we get tilings of the three-dimensional Lobachevsky space, into regular polyhedra. Only you need to be careful, you can not blow cubes too long, otherwise self-intersection of edges is formed (figure on the right). It is in the figure that our self-intersections have formed, and in the sense of the 3-dimensional Lobachevsky space, this means that the vertices of the cube have gone beyond the absolute. Thus, six cubes in the edge are denoted by the Schlefli Symbol {4,3,6} and already at this partition of the 3-dimensional Lobachevsky vertex space are located directly on the absolute. The {4,3,7} vertices already go beyond the absolute, these Schlefli Symbols also show partitions of the 3-dimensional Lobachevsky space, but strictly speaking, not into regular polyhedra, but into something else, here you can already figure out how to call these objects and agree about their name.We have worked with cubes, similarly get partitions from other three-dimensional regular polyhedrons.
{3,3} - tetrahedra, we combine three tetrahedra in the edge {3,3,3}, there is a gap, we inflate them before gluing the faces, we get a partition of the 3-dimensional sphere into tetrahedra, converging 3 pieces in the edge. This partition defines a regular polyhedron in the 4-dimensional Euclidean space {3,3,3}.
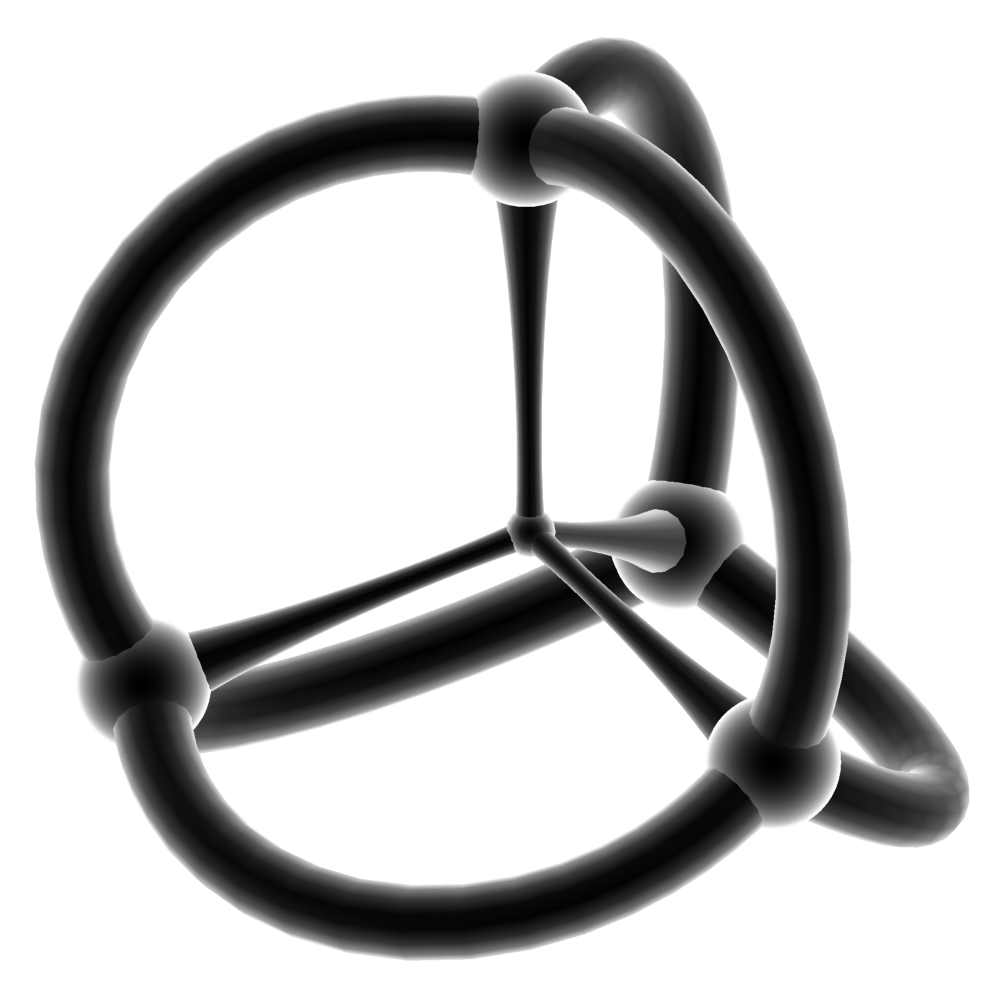
Fig.22 Splitting of the three-dimensional sphere {3,3,3}.

Fig.23 Four-dimensional polyhedron {3,3,3}
With the remaining partitions of the 3-dimensional sphere and polyhedra is similar.

Fig.24 Splitting of the three-dimensional sphere {3,3,4}.

Fig.25 Four-dimensional polyhedron {3,3,4}

Fig.26 Splitting of the three-dimensional sphere {3,3,5}.

Fig.27 Four-dimensional polyhedron {3,3,5}

Fig.28 Splitting of the three-dimensional sphere {3,4,3}.
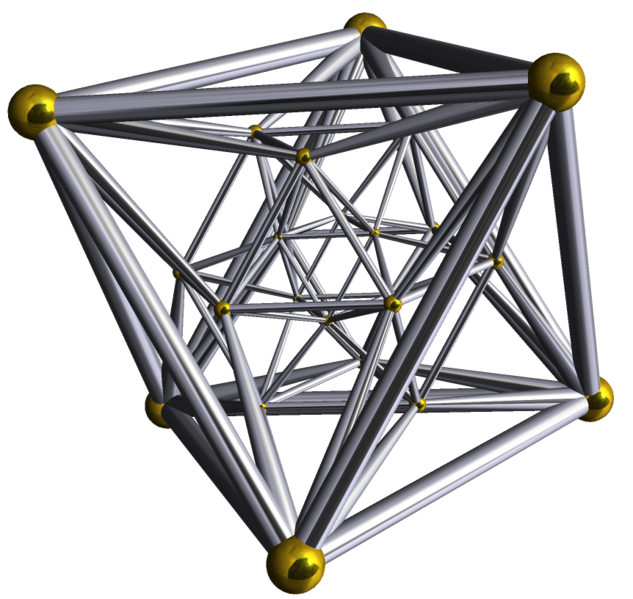
Fig.29 Four-dimensional polyhedron {3,4,3}
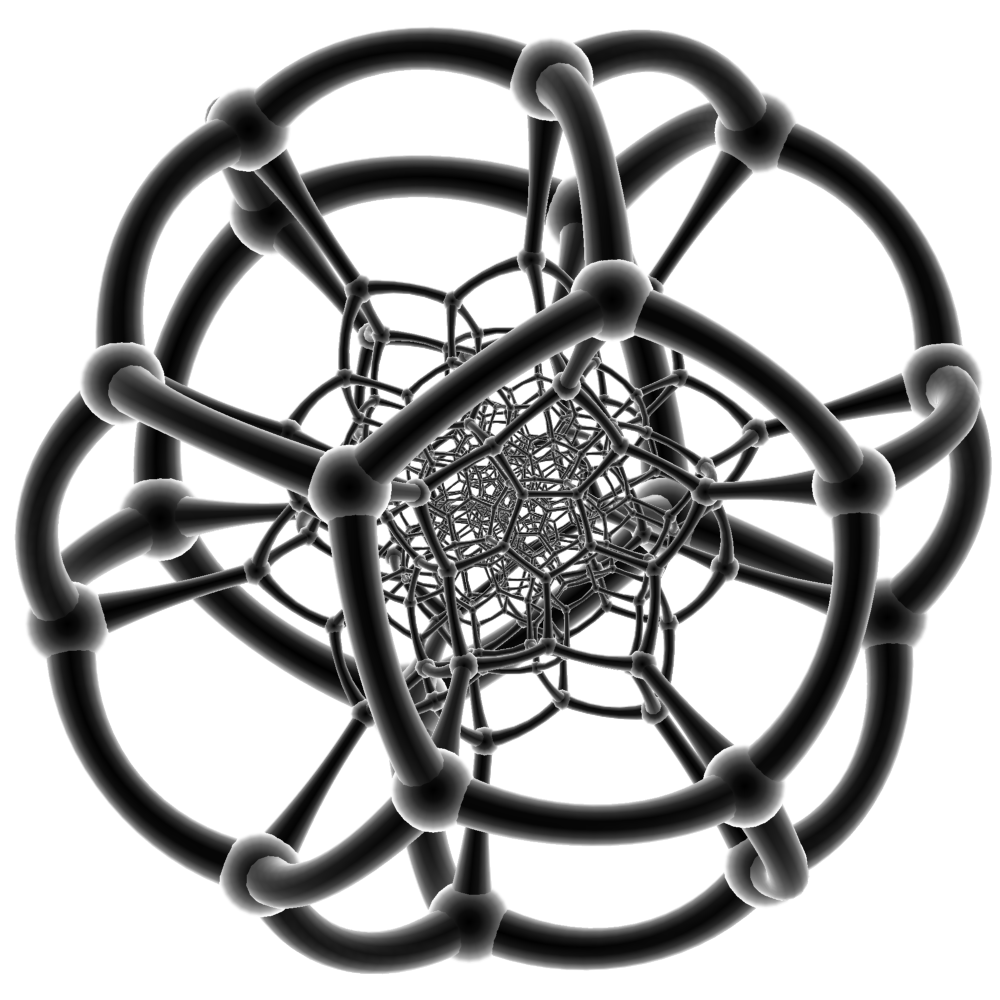
Fig.30 Splitting of the three-dimensional sphere {5,3,3}.

Fig.31 Four-dimensional polyhedron {5,3,3}
With the splittings of the 3-dimensional Lobachevsky space, everything is the same too, only the polyhedra need to be blown away and not forgotten that the tips do not fly out for absolute. Determining where the tips are located by the Schläfli Symbol is very easy, for {p1, p2, p3} we consider the Symbol {p2, p3}, if {p2, p3} breaks the Euclidean plane, i.e. takes one of the values {4,4}, {3,6}, {6,3}, then this is a sure sign that the tips {p1, p2, p3} are ON absolute, for example, {3,3,6}, { 3,4,4}, {3,6,3} and others. If {p2, p3} - breaks the Lobachevsky plane, then the vertices {p1, p2, p3} are FOR absolute, for example, it is {3,3,7}, {3,4,5}, {3,6,4} and others . If {p2, p3} - breaks a sphere, but at the same time {p1, p2, p3} - does not break a sphere, then {p1, p2, p3} - breaks a 3-dimensional Lobachevsky space, I’ll list all of these options: {4 , 3.5}, {3,5,3}, {5,3,4}, {5,3,5} there are no other such ones.
For polyhedra and partitions in other dimensions of spaces, the situation is completely the same. The Schläfli symbol for spaces of higher dimensions will be written {p1, p2, p3, p4, ... pn}
Learn to inflate and blow off the ball and you will have no difficulties with spaces of constant curvature.
And finally, a few words about the duality property of polyhedra. If the Schläfli Symbol is written in the reverse order, then we also get the correct polyhedron, only dual to the original one. So the octahedron and the cube are dual to each other, i.e. {3.4} - {4.3}. The tetrahedron is self-dual {3.3} - {3.3}. The icosahedron and dodecahedron are dual, {3,5} - {5,3}. This is a very important feature that helps calculate the size of the edges and angles of regular polyhedra. When constructing all the drawings that I used in the article, I used this property very actively. Also, when constructing a dodecahedron, the property that the cube clearly fits inside the dodecahedron turned out to be very important, and the cube vertices right on the vertices of the dodecahedron. This helped to find the coordinates of 8 vertices of the dodecahedron, the remaining vertices of the dodecahedron were not difficult to find. Here they are, polyhedra, very similar to each other. Geometrically, duality means that the vertices of one polyhedron abut against the centers of the flat faces of the second dual polyhedron to the first. On the example of three-dimensional polyhedra, all these properties are shown in the video.
You can download the source and experiment with polyhedra yourself: twist them, bend the edges, look at the duality.
Sources
Models of regular polyhedra
Bending ribs cube
Rib bending octahedron
There you will find a program for viewing and editing these drawings.
Bending ribs cube
Rib bending octahedron
There you will find a program for viewing and editing these drawings.
The duality property is also preserved in all other dimensions of spaces, so {3,3,5} is dual {5,3,3}, etc.
This article was created as part of a series of articles about the derivation of regular polyhedra in all dimensions:
Correct polyhedra. Part 1. Trimerie
Correct polyhedra. Part 2. Foursome
Correct polyhedra. Part 2.5 (auxiliary)
Schläfli symbol. Part 2.6
The ultimate goal of these articles is to show the derivation of all regular, convex polyhedra in dimensions 3 and higher. After the publication of Part 2, I felt that the material was badly received, I thought about the reasons for a long time and came to the conclusion that the people were simply not familiar with such a simple but powerful tool as the Schläfli Symbol, so I wrote this article. The next article is Part 3, where it will be necessary to make an inductive transition along the dimensions of space and obtain the final formula for the dihedral angles of polyhedra and the polyhedra themselves.
Thanks for attention. In touch. Until.
Source: https://habr.com/ru/post/310570/
All Articles