Review of the tasks of the final round of the RCC 2016

On September 18, the last, final stage of the 2016 Russian Code Cup sports programming championship was held. Gennady Korotkevich took the first place in a bitter struggle, the second and the third places - Vladislav Epifanov and Nikolai Kalinin, respectively.
The final table can be found here , the prize fund for the first time this year is distributed to the first 25 places in the ranking. This is not the only innovation - for the first time, English-speaking programmers, of whom more than a thousand out of 4.5 thousand participants, had the opportunity to participate in the RCC, had the opportunity to participate. In addition to traditional CIS countries for the competition, representatives of Germany, Finland, Japan, Switzerland, China and South Korea fought in the final round. In addition, this time there was a mirror round at Codeforces - right after the final of the main competition, everyone had the opportunity to solve the final tasks in a specially organized competition for the first division, a little more than 200 programmers participated.
')
Traditionally we offer you an analysis of the final tasks (tests can be downloaded here ):
A. Closing ceremony
B. Cactus phobia
C. Homework
D. Slalom
E. Code
F. Coating array
A. Closing ceremony
Time limit of 2 seconds
256 MB memory limit
Condition
The closing ceremony of the Squanch Code Cup is held in a large hall for n × m people. The hall itself consists of n rows, each of which contains m chairs. Each chair has two coordinates: ( x , y ) (1 ≤ x ≤ n , 1 ≤ y ≤ m ).
Two queues crowded the entrance to the hall: k people are at the point with coordinates (0, 0), and n · m - k people are at the point with coordinates (0, m + 1). Each person must have a ticket to a certain place. If a person has p with initial coordinates ( x , y ) a ticket for a seat ( x p , y p ), he will need to pass | x - x p | + | y - y p |.
About each person is known for his endurance, namely what is the maximum distance he can walk. Your task is to find out whether it is possible to distribute all the tickets so that each person can reach his place.
Input Format
The first line of input contains two positive integers n and m (1 ≤ n · m ≤ 10 4 ) - the size of the hall.
The second line contains several non-negative integers. The first number k (0 ≤ k ≤ n · m ) denotes the number of people with initial coordinates (0, 0). It is followed by k numbers denoting the endurance of these people.
The third line contains several non-negative integers. The first number l ( l = n · m - k ) denotes the number of people with initial coordinates (0, m + 1). It is followed by l numbers denoting the endurance of these people.
Endurance is given by natural numbers not exceeding n + m .
Output format
If it is possible to distribute tickets in the manner described, output "YES". Otherwise, print "NO".
Examples
Input data:
2 2
3 3 3 2
13
Output:
YES
Input data:
2 2
3 2 3 3
12
Output:
NO
In the problem, well-written solutions with asymptotics of no more than O (( nm ) 2 ), which correspond to the description of this greedy algorithm, were performed. If you use the set, then the asymptotics can be reduced to O ( nm log ( nm ))
B. Cactus phobia
Time limit of 2 seconds
256 MB memory limit
Condition
A tree is a connected undirected graph without cycles. The rib cactus is a connected undirected graph without loops and multiple edges, in which each edge lies on no more than one simple cycle.
Vasya has a rib cactus in which each edge is painted in some color. Vasya wants to remove the minimum number of edges from the cactus so that it turns out a tree. At the same time, he wants the maximum number of different colors among the remaining edges. Help him find out how many different colors can stay in the graph.
Input Format
The first line contains two integers n , m (2 ≤ n ≤ 10 000) - the number of vertices and edges in the Vasya graph, respectively.
The following m lines contain three integers u , v , c (1 ≤ u , v ≤ n , u ≠ v , 1 ≤ c ≤ m ) - the vertices that connect the next edge and its color. It is guaranteed that the described graph is a costal cactus.
Output format
Print a single integer - the maximum number of different colors that can be left in the graph.
Examples
Input data
4 4
1 2 4
2 3 1
3 4 2
4 2 3
Output
3
Input data
7 9
1 2 1
2 3 4
3 1 5
1 4 5
4 5 2
5 1 6
1 6 4
6 7 6
7 1 3
Output
6
We construct a bichromatic graph in which the left beat is a block, the right one is a color. From the block we will draw edges in each color that is in this block (if the color occurs several times, we will draw several edges). From the colors of the ribs to the drain. From the source of the edge to the block, if the block is a bridge, then with a throughput of 1, otherwise with a throughput of 1 less than the cycle length. It is easy to see that the maximum flow in this graph will be the answer.
Even in this problem there is a solution that does not use threads, and working for O ( n ), we suggest inventing it as an exercise.
C. Homework
Time limit 3 seconds
256 MB memory limit
Condition
Today, Petya behaved badly in a mathematics lesson, and the teacher punished him by giving him extra homework. She called him three numbers n , m and k and told him to mark one or several cells on a rectangular checkered board of size n × m . Marked cells should form a connected figure. In this case, there must be exactly k ways to select the three marked cells so that they form a “corner” - all three selected cells lie inside a 2 × 2 square.
A set of cells forms a connected figure, if from any cell of the set one can get to any other one, moving from the cell to the neighboring side in the process. Petya knows that the task is not easy, so he asked you, as a programmer and best friend, to help him with this task.
Input Format
The input contains several test cases. The first line contains the number of tests t (1 ≤ t ≤ 100). Each of the following t tests is described by one line of three numbers n , m and k (3 ≤ n , m , n × m ≤ 10 5 , 0 ≤ k ≤ 10 9 ). It is guaranteed that the sum of n × m for all tests does not exceed 10 5 .
Output format
For each test output the answer to it. If the answer exists, output n lines with m characters each, where '*' means the marked cell, and '.' - unchecked. If there is no answer, output -1 in the only line. After each test, except the last, output an empty line.
Examples
Input data
3
3 3 4
3 3 5
3 3 3
Output
**
**
...
***
**
...
. **
**
* ...
- To simplify the analysis of cases for all n , m <5, we run a full search. Here, in order to avoid non-asymptotic optimizations and meet the TL, it was worthwhile to make a preliminary calculation.
- Now, without pleading for generality, we can assume that m ≥ 5.
- Let's start arranging asterisks in a row on the table (along the lines from top to bottom, in each row from left to right). When you add each asterisk (except extreme) adds 4 new corner. When adding an asterisk to the end of the line, 3 new corners are added, to the beginning - 1. Stop the process as soon as k becomes less than 4 or as soon as there are less than 5 free cells in the table.
- Further developments are divided into two cases:
- left free line
- no free line left
- The first case. Once a free line is left, it means we broke off, because k is less than 4. Then:
- k = 0: do not add anything, everything came together
- k = 1: if the current line has ≥ 2 asterisks, we put an asterisk at the beginning of the next line, and if not, then at the end of the current line
- k = 2: if the current line contains ≥ 3 asterisks, put an asterisk in the second column of the next line, and if not, in the next-to-last cell of the current line
- k = 3: if ≥ 4 stars are already in the current line, we put asterisks in the first and third columns of the next line. If three are set, we put in the second column the next and in the last but one current one. If two - at the beginning of the next line and in the pre-penultimate column of the current one. If there is one, we put asterisks in m - 1 and m - 3 columns of the current line (numbering from zero).
- The second case. There are 4 free cells left in the table, where you can put asterisks. By a simple search of the cases, it is possible to deduce that, putting asterisks in these cells, one can get the following values of k : {0, 1, 2, 3, 4, 5, 6, 8, 9, 12, 15}. The analysis of these cases remains to the reader as an exercise.
- It was also worth not forgetting about the case of a 3 × m rectangle, where m ≥ 5 and k = 2 * ( m - 1) - 8 - in this case, leave the first column empty, and fill the rest of the columns completely.
D. Slalom
Time limit of 2 seconds
256 MB memory limit
Condition
Girl Masha loves winter sports, and today she has to go skiing. The track is schematically a n × m checkered rectangle. On the field there are rectangular obstacles that occupy some cells. Masha should get from the cell with coordinates (1, 1), into the cell ( n , m ). At the same time, from each cell one can move either one cell up or one cell to the right. In the cells in which the obstacles are located, you can not fall.
Thus, each obstacle can be circumvented in two ways: it will remain either to the left of the trajectory of movement along the track, or to the right. Masha loves diversity, and she wonders how many different ways there are to pass the track. Passages of the route are considered different if there is at least one obstacle that is in one passage to the left, and in the other to the right of Masha's trajectory.
Your task is to help Masha find out the number of different ways to pass the track. The answer can be large and Masha will arrange a value modulo 10 9 + 7. In the figures below, tests from the condition are analyzed.
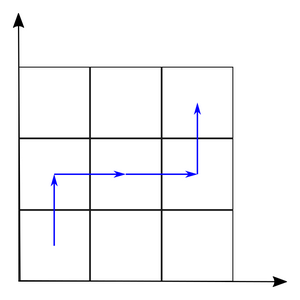

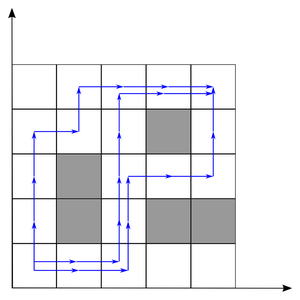
Input Format
The first line of the input data contains three natural numbers n , m and k (3 ≤ n , m ≤ 10 6 , 0 ≤ k ≤ 10 5 ) - the dimensions of the route and the number of obstacles, respectively. The following k lines contain four natural numbers x 1 , y 1 , x 2 , y 2 (1 ≤ x 1 ≤ x 2 ≤ n , 1 ≤ y 1 ≤ y 2 ≤ m ) - the coordinates of the lower left and right upper corner of the obstacle . It is guaranteed that there are no obstacles in the cells (1, 1) and ( n , m ), and all the obstacles have no intersections (but they can touch).
Output format
In the output file output a single number - the remainder of dividing the number of different ways to pass the track by the number 10 9 + 7.
Examples
Input data
3 3 0
Output
one
Input data
4 5 1
2 2 3 4
Output
2
Input data
5 5 3
2 2 2 3
4 2 5 2
4 4 4 4
Output
3
We will solve the problem by dynamic programming. For each class, we will consider the lowest path: the sum of the heights of the cells through which it passes is minimal. The state of dynamic programming is the number of such lower paths passing through a given cell. Then, when we encounter an obstacle, all the paths that pass through the cells below its top can be divided into two, if there is no other obstacle above them that would prevent this. That is, when processing an obstacle in a cell above its upper boundary, it is necessary to add a sum of values in the cells below its top, the paths of which have the opportunity to separate.
The naive implementation of this algorithm required O ( nm ) memory and O ( nm 2 ) time, so you need to use a segment tree to optimize the counting of the sum during transitions of dynamic programming, and also not to store the entire field, but only the current column. Thus, O ( m ) memory is obtained, and the running time is O ( n log m ).
E. Code
Time limit of 2 seconds
256 MB memory limit
Condition
Recently, Boris saw a large electronic scoreboard. A number is encrypted on the display. The number itself consists of n digits, each of which is written using a small Latin letter. Next to the scoreboard is a label that describes the encryption scheme. So, for each digit i and digit j , the symbol c is known by which it is encoded. In this case, different numbers may correspond to the same letters. Every second the number that is encoded on the scoreboard increases by one. A second after all the n digits of the number, encrypted on the scoreboard, are equal to nine, the scoreboard makes a very loud sound.
Andrei knows what number was encrypted on the board at the very beginning. He wondered how many seconds Boria would be able to pinpoint that number. Consider that Borya can accurately measure time, and also that the first time the number on the scoreboard will change exactly a second after Borya saw the scoreboard.
Input Format
The first line contains an integer t (1 ≤ t ≤ 100) - the number of test cases. The description of each test begins with the number n (1 ≤ n ≤ 18) - the number of characters in the encrypted number. The next line contains n digits without spaces (possibly with leading zeros) - an encrypted number. The next n lines contain ten characters each. If the j- th character in the string i equals c , then the digit j - 1 in the i- th digit (the higher bits are described earlier) is encoded with the letter c .
Output format
For each test case on a separate line, print a single integer without leading zeros - the minimum number of seconds that is needed to decipher the number.
Examples
Input data
3
2
42
abcdefghij
jihgfedcba
2
42
aaaaaaaaaa
aaaaaaaaaa
one
2
abcdabcdff
Output
0
58
2
The basic idea of the solution is that we do not need to check that the number can be distinguished from all 10 n - 1 others. It is argued that if we can distinguish a number from the same one in which exactly one digit was changed, we can also distinguish it from all other numbers. Thus, it is necessary to find out the first moment in time when it is possible to distinguish a number from 9 n others.
Note that this subtask can also be solved in less than 10 n . To do this, let's sort the digit, by which it will be possible to distinguish two numbers, as well as its value. After that, we will find the first moment in time, when one of the numbers will take just such a value and check whether we can distinguish two numbers. Thus, we obtain a solution that works in polynomial time based on the number of digits.
F. Coating array
Time limit 3 seconds
256 MB memory limit
Condition
Misha has an array of n integers. He wants to choose k different sub-sections in it so that for each element of the array there is at least one selected segment that contains it. At the same time, Misha wants to sum up the numbers on each segment, and then sum up the resulting amounts, then the total amount was the maximum.
Input Format
The first line contains two integers n , k (1 ≤ n ≤ 100 000, 1 ≤ k ≤ n · ( n + 1) / 2) - the number of elements in the array and the number of segments to be selected.
The second line contains n integers a i (- 50 000 ≤ a i ≤ 50 000) - the elements of the array.
Output format
Print a single integer - the maximum sum of the sum of numbers on the segments, which can be achieved by choosing k segments so that each element is covered by at least one segment.
Examples
Input data
5 4
6 -4 -10 -4 7
Output
eleven
A little distracted. Consider how you can solve the problem for n 2 log n . Let us sort out x - the number of maximum total segments in the answer ( O ( n ) variants, since min ( k - n , 0) maximum segments will be included in the answer necessarily). Let the elements with indices i 1 , ..., i m remain uncovered, and we need to cover them using k - x segments. , k - x i j -, - i j -. k - x , l - i j , l + 1- i j + 1 , - [ i j + 1; i j + 1 - 1], - [ i j + 1; i j + 1 - 1]. , [ i j + 1; i j + 1 - 1] , , — , ( i 1 ), ( i m ), k - x . , n 2 log n .
, [ i j + 1; i j + 1 - 1] . i j -, ( O (1), ), k - x . i j - O ( n ), O ( n log n ).
***
Russian Code Cup Mail.Ru Group, IT- IT.Mail.Ru . IT.Mail.Ru , IT . Russian AI Cup, Russian Code Cup Russian Developers Cup, . , . . . . , IT.Mail.Ru , IT, IT-.
Source: https://habr.com/ru/post/310376/
All Articles