The logic of consciousness. Part 6. The cerebral cortex as a space for calculating meanings.

What is information, how to find the meaning hidden in it, what does it all mean? In most interpretations, information is compared with a message or with data, using these words as synonyms. The message usually implies a specific form. For example, oral speech, text message, traffic signal and the like. The term "message" is often used when talking about information in connection with its transfer. Data usually means information for which the form of its storage or transmission is determined. For example, we talk about data when we mention records in a database, arrays in computer memory, network packets, and the like. We prefer to use the term “information” when there is no need to focus on the mode of its transmission or the form of presentation.

The information to be used must be interpreted. For example, a red light can be interpreted as a prohibition to drive, a smile as a signal of good location, and the like. The concrete interpretation is called the meaning of information. At least, such an interpretation is followed by the international organization for standardization : "knowledge concerning objects, such as concepts, events, things, processes, or ideas, including concepts,

Different interpretations may exist for the same information. The interpretation of the message “computer power button is pressed” depends on the state, turned on or not, of the computer before it was pressed. Depending on this information can be interpreted as either "on" or "off".

Circumstances that determine how this or that information should be interpreted are usually called context. The interpretation of information exists only in a specific context. Accordingly, the meaning found in the information also applies to a specific context.
')
The same information can have its meaning in different contexts. For example, all aphorisms are built on this: “A window to the world can be closed with a newspaper”, “It’s easy to make a chain out of zeros”, “They say that a person who has lost his teeth is somewhat looser” ( Stanislav Jerzy Lets ).

What interpretation will be chosen by the person for this or that information, in many respects, is determined by his personal experience. Someone can see one thing, someone else: “when a fool is shown on stars, a fool sees only a finger” ( Amelie film, 2001).

The given correlation of information, context and meaning of information is intuitively clear enough and agrees well with our everyday experience. In the previous part I tried to show how all this can be transferred to a formal model with simple rules:

• The subject has a finite set of concepts;
  
• Any description is a set of concepts;
  
• Context is a set of rules for translating one concept into another;
  
• A treatment is a new description, obtained in context, after applying the transformation rules;
  
• The context space is the set of all contexts accessible to the subject;
  
• Meaning is a set of interpretations that have a plausible appearance. That is, such that in a certain way are consistent with the memory of the subject.
  

Winston Churchill said: "There are no facts, there are only their interpretations." Information that has received a correct interpretation acquires meaning. From the obtained interpretations, the memory of the subject can be formed.

If there are examples of the original messages and their correct interpretations, then we can distinguish the rules of interpretation applied in each case of interpretation. It’s like translating from one language to another. The same word in different circumstances can be translated differently, but for a particular sentence and its translation it is always clear which option was used.

If we analyze what the choice of this or that interpretation depends on, it turns out that there is a finite set of circumstances that influences this choice. Such circumstances are contexts. Within one context, there are agreed upon rules of interpretation for all concepts at once. In language translation, this corresponds to how the subject or subject area determines which version of the translation is more appropriate.

A set of contexts can be obtained automatically from the clustering of pairs “original description - correct interpretation”. If couples are combined into classes, the rules of interpretation of which do not contradict each other, then the resulting classes will correspond to the contexts, and the rules collected from all pairs of the class will be the rules for the interpretation of this context.

If contexts are formed, then the search for meaning in information is the determination of which context is best for its interpretation. In inappropriate contexts, interpretations look "crooked" and only in the right context does the "correct" interpretation arise. One can understand how correct or incorrect the interpretation looks like by how similar it is to the “correct” interpretations already stored in memory.

There are two main ideas associated with the selection of contexts. The first is that, using contexts, we get the opportunity to give reasonable interpretations of the information that we have never met before. So when translating, when we know both languages ​​well, we still don’t remember all possible sentences and their translations. Understanding the context of the conversation, we select the translation options for individual words that are most suitable for this context. The second idea is that memory, that is, previous experience, allows you to determine which context in this situation creates the most correct interpretation.

A small example: suppose we are dealing with geometric shapes. We were shown a triangle, and then showed a circle. We remembered these descriptions. Then we were shown the same triangle, but with an offset. The descriptions did not match. If we want to recognize a triangle in any displacement, then we can try to memorize its descriptions in all possible displacements. But this will not help us after seeing the circle again, to recognize it in the displacement. But you can learn the rules by which the descriptions of shapes change at certain offsets. Moreover, these rules will be the same and will not depend on the specific shape. Then it will be enough for us to see any figure once, in order to immediately recognize it in any displacement.

An algorithm for determining the meaning of information was proposed. The original description in each of the contexts that form the context space gets its interpretation. That is, as many possible interpretation hypotheses are built as there are possible contexts. If in any context the resulting interpretation turns out to be similar to the contents of the memory, then this interpretation gets a chance to become the meaning of information.

For geometric shapes, this means that each context stores the rules for changing descriptions for a particular offset. The number of contexts is determined by the number of possible offsets. Having seen the square on the right above, we will have to apply our offset to it in each context and get all possible variants of its location. If we have previously seen a similar square, for example, in the center, then in one of the contexts the current interpretation coincides with what was remembered earlier.

A computational scheme was proposed. Each context is served by its own computing module. The same description goes to the input of each module. The memory of each module contains the rules for the transformation of concepts for its context. In each context, an interpretation is obtained that is compared with memory. According to the degree of correspondence between the interpretation and the memory, it is determined whether there are contexts in which the information takes on a meaningful form.



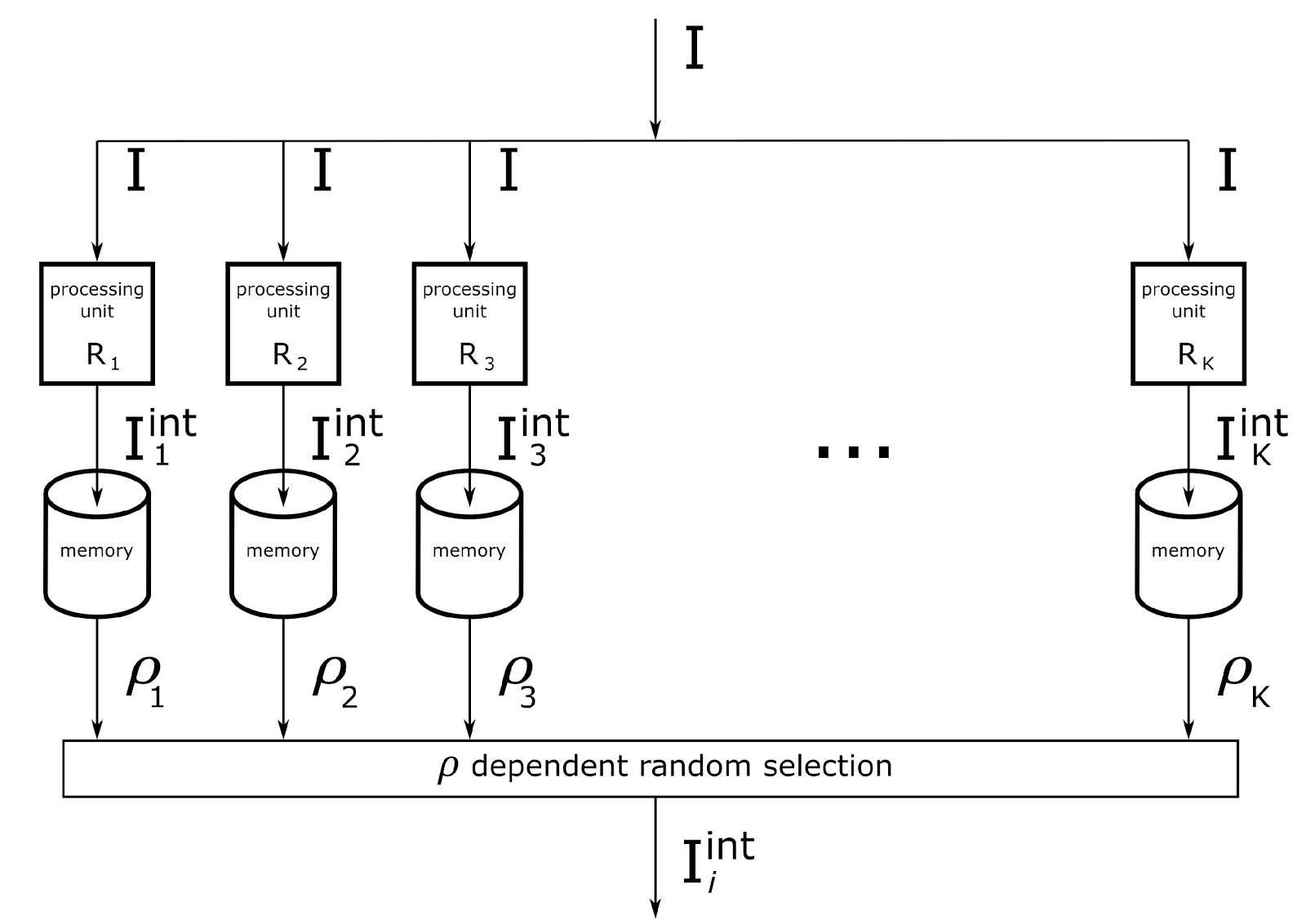
In the previous part it was shown that many types of information faced by a person are reduced to a similar computational scheme.

The work of contextual computing modules requires that:

• Information was presented as a set of discrete concepts.
  
• Each context module received the same information;
  
• Each context module had a memory of its own rules for transforming initial concepts into their interpretations;
  
• Each context module could, independently of the others, access memory, which stores all previous experience, and evaluate the reliability of its interpretation hypothesis.
  

What in the cortex can be such a computational element with its autonomous memory? So, it seems, it is time to talk about cortical minicolumns.

Brain

A little refresh in the memory of the general structure of the brain. Basically, it consists of an ancient brain, cortex, white matter and cerebellum.

The ancient brain is located in the center and occupies a relatively small volume. It is called ancient for the reason that it is very similar in many living beings and, apparently, determines the basic evolutionary basic functions that are common to all of them.


Ancient brain, white matter and cortex

The outer surface of the brain consists of a thin layer of neurons and glial cells. This layer is called the cerebral cortex. The more a biological species is at a higher stage of evolutionary development, the more developed is its bark.

When the bark reaches a large area, for example, as in humans, it begins to form folds. The task of the folds is to fit a large surface area of ​​the cortex into a relatively small volume of the skull.

It is known that the cortex acquires its functions in the learning process. This is confirmed, for example, by the following fact. If any part of the cortex is damaged, such as stroke, removal or injury, the functions associated with this place are lost. But over time, these functions can recover. The remaining part of the same area of ​​the cortex can re-learn the lost skills, or the symmetrically located area of ​​the other hemisphere assumes such a replacement function.

The region of the cortex that is responsible for a particular functional is called the cortex zone. The whole crust is divided into many such zones.



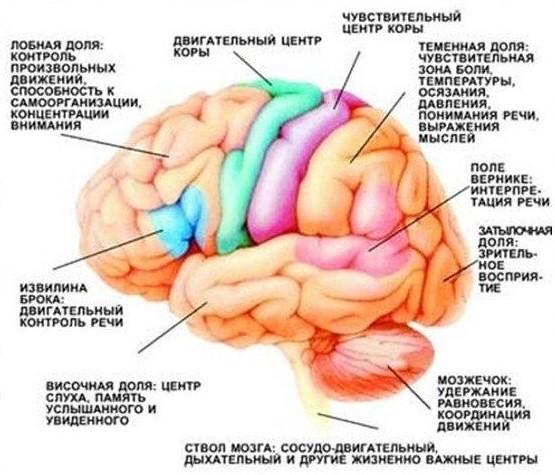
One of these zones, the motor zone of the cortex, is responsible for our physical activity. But the commands issued by this zone are of a general nature. Accurate motility, that is, the detailed implementation of these commands into signals to the muscles, is performed by a separate organ, the cerebellum.



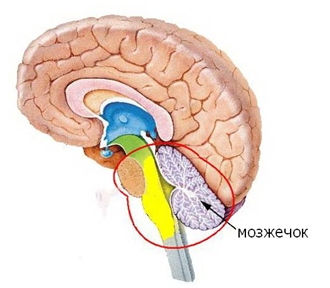
The cerebellum has been named for what looks like a miniature brain. By the way, it is not always miniaturized, for example, in sharks the cerebellum is larger in volume than the main brain. It is noteworthy that the outer surface of the cerebellum is also a cortex. The cerebellar cortex is somewhat different from the cerebral cortex, but it is very likely that the ideology of its work should be very close to the work of the cerebral cortex.



The space between the cerebral cortex and the ancient brain and inside the cerebellum is filled with white matter. This is nothing more than axons of neurons that transmit signals from one part of the brain to another (figure below).


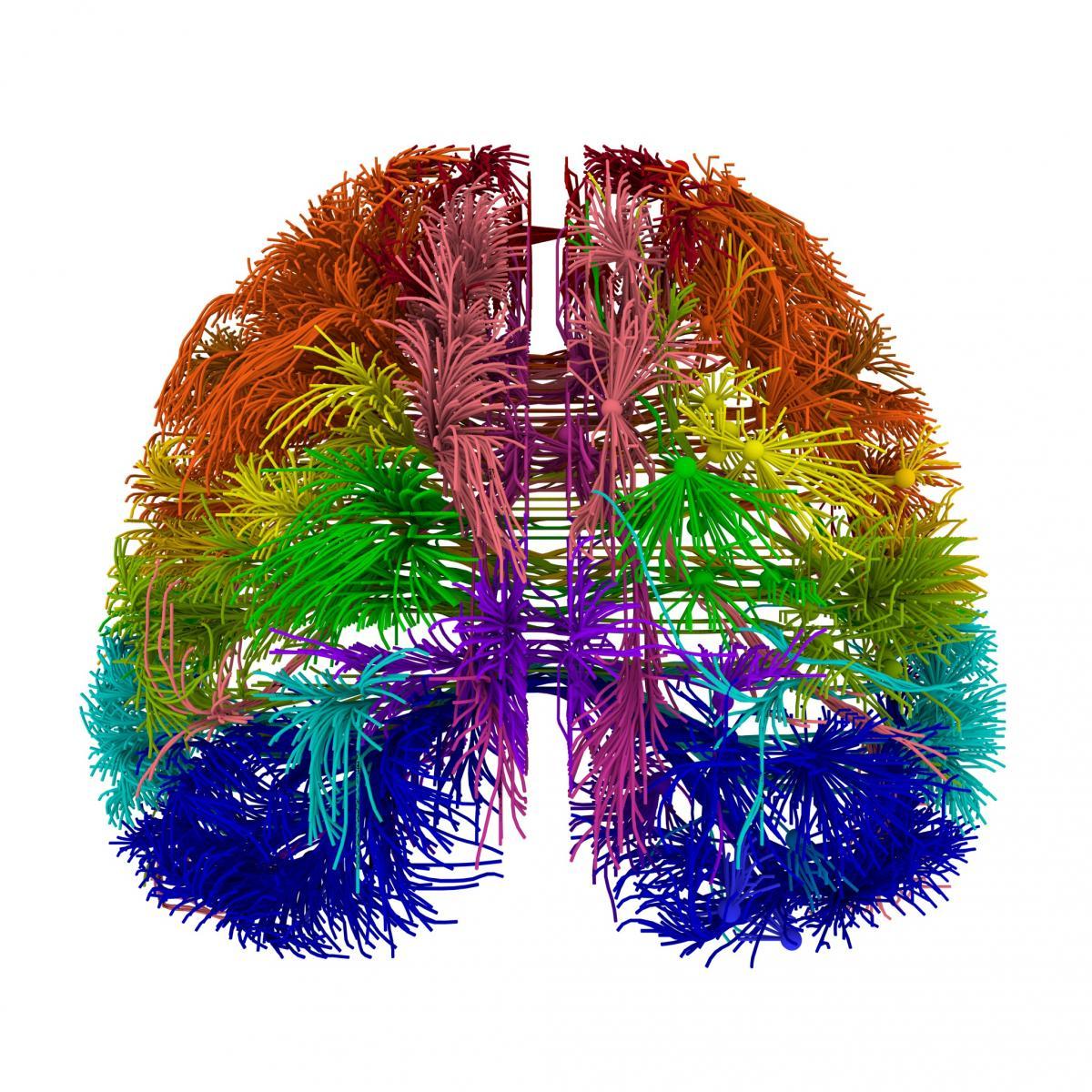
The projection connection of the real brain. Separate “strings” correspond to bundles of nerve fibers (Allen Institute for Brain Science)

These connections are well studied. They are not just a continuous projective environment, but something much more interesting.

In artificial neural networks using deep learning, information is transmitted from level to level. Usually, a layer has an input neuron layer, hidden layers and an output layer.


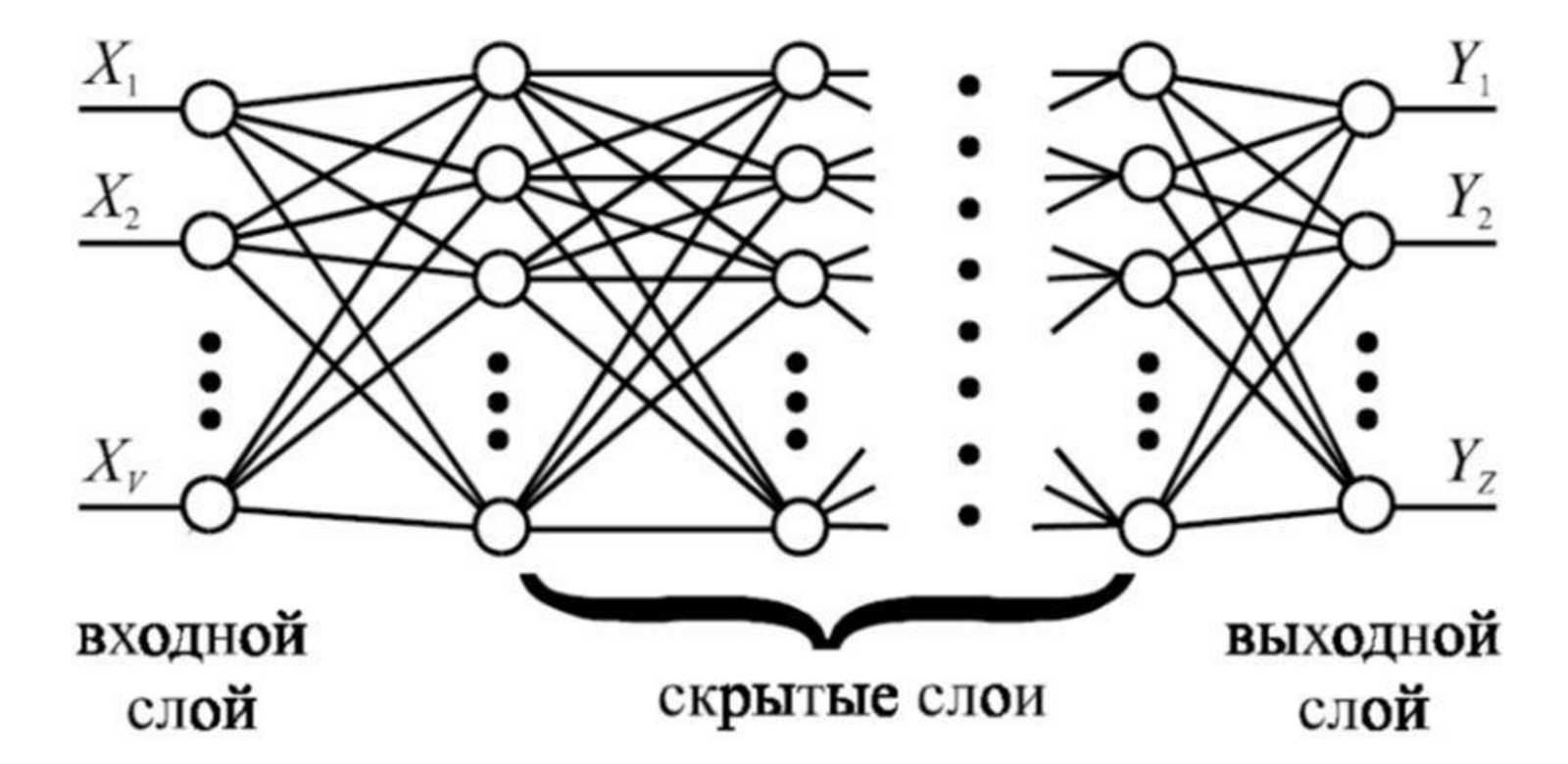
An example of a direct distribution network

The figure above shows one of the possible options, but, in general, the level can be quite complex inside. For example, a layer can perform convolution operations and have a completely different architecture. But common to all levels is that they have an input and output layer on which information is encoded by a set of features. One neuron - one sign. The collection of neurons in the layer is an indicative description. About each neuron of the input and output layer, we can say that it corresponds to its own grandmother.

To transfer the state of one network level to another, it is required to transfer the state of all neurons of the output layer of the initial level to the neurons of the input layer of the next level.

The transmitted description itself is obtained by a long vector consisting of binary features. In this approach, the number of signs is limited by the number of neurons in the output layer, and the transfer from level to level requires as many “fiber connections” as the transmitting neurons.

So, nothing even closely resembles the real brain system. The zones of the cortex are connected with each other and with the structures of the ancient brain by thin bundles of fibers. The fibers that make up the bundle point out from one spot and also point to the other. There are only a few hundred fibers in each bundle. In the picture above, each visible “thread” is this bundle.

It can be assumed that the information on such bundles is transmitted not by a feature description, where one fiber is one feature, but a code (picture below), when the pattern of fiber activity encodes a transmitted concept.


Bundle of nerve fibers (left) and sample code (right)

Using the example of the projection system, we clearly see the difference between the proposed model and the models with neuron detectors. A neuron signal, if it is a grandmother's neuron, implies an indication of whether or not there is a grandmother in the current description. In our model, the activity of a neuron is just a bit in a binary code.

When it is found that a real neuron reacts steadily to a certain stimulus, one cannot conclude from this that the neuron and the stimulus correspond. The same neuron can successfully respond to other stimuli.

The transmission of information through projection beams can be compared with the transmission of binary signals over computer data buses. This is a fairly accurate analogy. Somewhat later, using the example of the visual system, I will give fairly strong evidence of the validity of such an assumption.

Summarizing what was said:

• The brain does not operate with characteristic descriptions in which the activity of neurons corresponds to some “grandmothers”, but with “digital” codes of discrete concepts;
  
• For learning, information processing, memory is responsible bark;
  
• The cortex consists of zones that perform specific functions. At the same time, regardless of what functions this or that zone performs and with what information it works, the architecture of the cortex remains almost unchanged. This means that it is possible to assume that in all places of the cortex the same principles of working with information are used, be it the bark of the big hemispheres or the cerebellar cortex.
  

Minicolumns bark

On the cut, the bark looks like the one below. A sufficiently thin layer, about one and a half millimeters from the surface, is filled with neurons and glial cells, then a white substance, consisting of axons, begins.


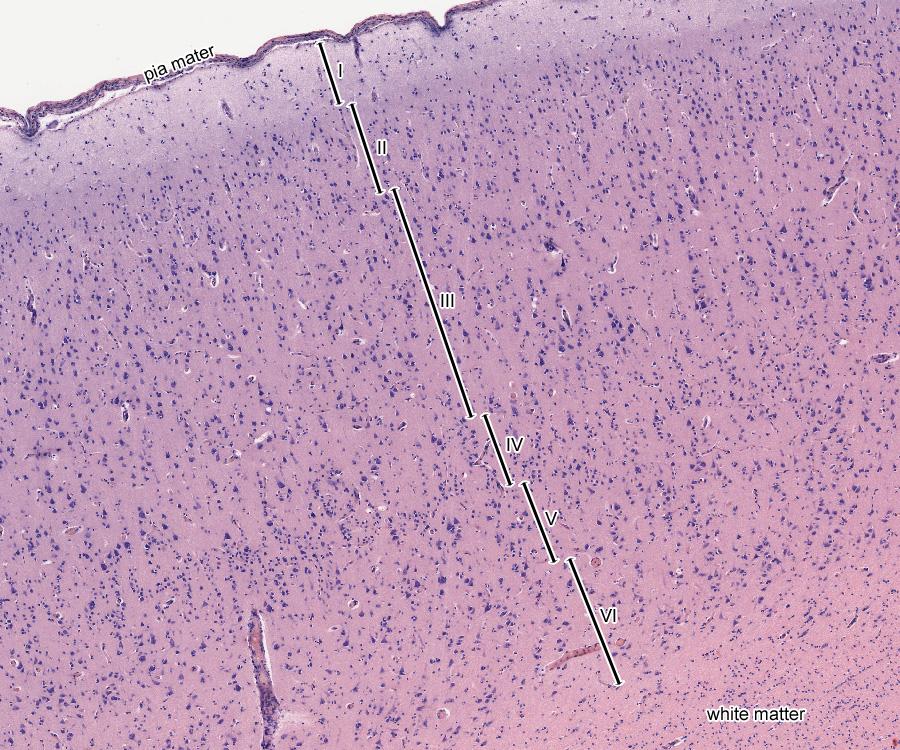
A cut of the cerebral cortex. The total thickness of all six levels is approximately one and a half millimeters.

The bark is divided into six layers. The upper first layer of the bark mainly contains horizontal axonal bonds and is similar to white matter. In the remaining layers, axon bonds, mainly, extend vertically. As a result, it turns out that the neurons vertically located under each other are interconnected much more strongly than with the neighboring neurons located to the left and to the right of them. This leads to the fact that the cortex "breaks up" into separate vertical columns of neurons. The look of a single neuron, column and column group is shown in the figure below.


Separate pyramidal neuron (left), cortical minicolon (in the middle), a fragment of the cortex consisting of a plurality of minicolumns (right) (modeling BBP / EPFL 2014)

A group of neurons located vertically under each other is called a cortical minicolon. Vernon Mountcl. Hypothesized (V. Mountktsel, J. Edelman, 1981) that for the brain the cortical column is the basic structural unit of information processing.

From 80 to 120 neurons are included in one minicolumn depending on the area of ​​the cortex, up to 200 neurons in the primary visual cortex of the minicolon (figure below).


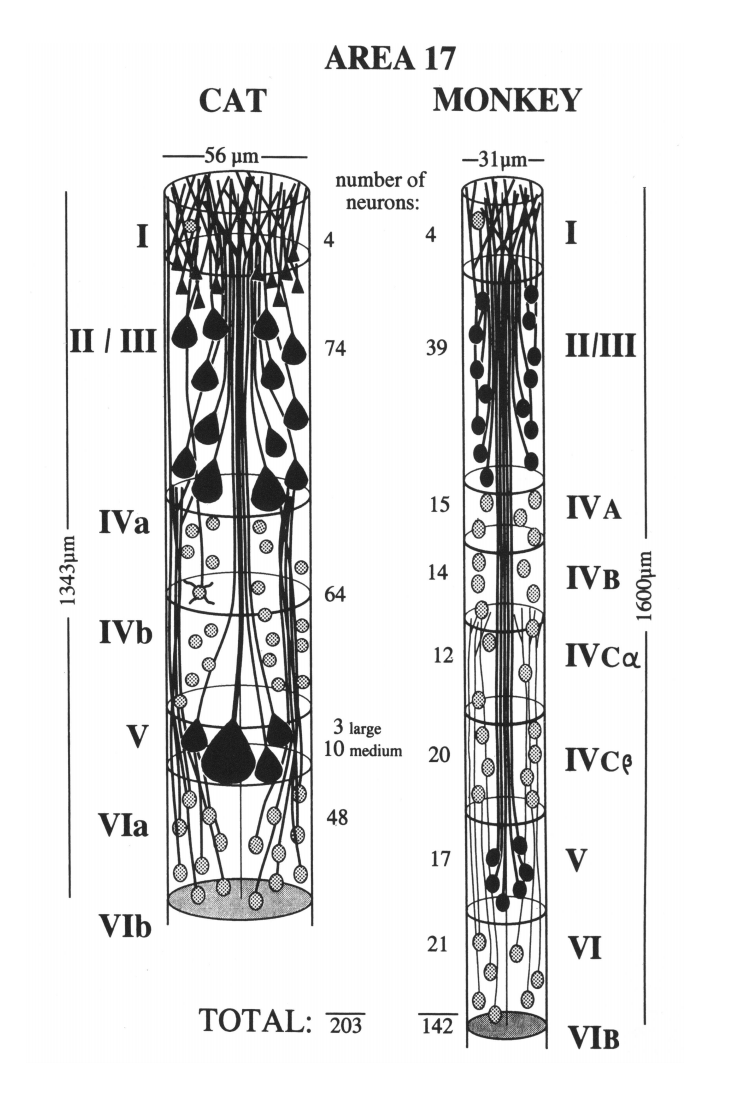
Minicolumns of the cat's primary visual cortex (left) and monkey (right) (Peters and Yilmaze, 1993)

The distance between the centers of minicolumns in the brain of a human or macaque varies from 20 to 80 microns depending on the zone. The transverse diameter of minicolumns is on average about 50 µm (Brain (1997), 120, 701–722, The Vernon B. Mountcastle). As I have already said, a large number of vertical connections are characteristic of microcolumns. Accordingly, a substantial part of the synaptic contacts inside the minicolumns fall on neurons belonging to the same minicolumns.

In order to understand what mini speakers are capable of, first we will try to estimate the memory capacity of one mini speaker.

Amount of memory for one minicolumn

Neurons have branched dendritic trees consisting of many branches. We assumed that information could be transmitted along the cortex in the form of propagation of interconnected patterns. The patterns themselves are supposedly patterns formed by the electrical activity of dendritic branches. One pattern evokes a continuation pattern associated with it. This process is repeated. As a result, a wave with a unique internal pattern rolls along the cortex. Each pattern corresponds to a concept.

Earlier, a memory formation scheme was shown, built on the interference of two wave patterns. The first pattern defines the elements that should preserve the memory. The second pattern sets the key memories.

The pattern of activity of dendritic branches inside one mini column causes the signal response of the neurons of this mini column. This answer looks like a picture of synchronous spikes. This neuron signal is a hash code for the original dendritic signal.

The hash transform from the “long” dendritic pattern of the key creates a short key of memories on the neurons. When a neural code appears, spikes begin to spread along the axons of the neurons entering this code.
Axons of neurons of one minicolumn form a set of synapses inside their minicolumn. From each synapse belonging to an active neuron, a neurotransmitter cocktail is distinguished. It turns out a complex picture of the volume distribution of signal substances.

Since neurotransmitters are thrown out of synapses, this picture is available for observation to all receptors that are nearby. Receptors are special molecules located on the surface of neurons and glial cells. Receptors can react to the appearance of a certain combination of chemicals and trigger various processes within the neuron. In addition, receptors can change their state and become sensitive or insensitive to certain signals.

Each minicolon neuron activity code creates a unique volumetric pattern of neurotransmitter distribution. We have shown that due to changes in metabotropic receptors, any segment of the dendrite can be memorized and subsequently learn with high accuracy any picture of the volume distribution of neurotransmitters. Moreover, the number of pictures that can be remembered by one dendrite branch is determined by the number of receptors and amounts to tens and hundreds of thousands.

In order for the signal of neurons to be remembered by the dendritic branch, there must be a place on it that is chosen relative to this signal. That is, a place where a substantial part of the axons of active neurons intersect. It was shown that for any signal on any dendritic branch with high probability there will be at least one such place.

A single cortical minicolon meets all the conditions necessary to preserve and reproduce memories. The diameter of the minicolumn corresponds to the elementary volume necessary for the formation of the spatial signal. Minicolon neurons can, with their activity, generate a binary key, the length of which is sufficient to uniquely identify any information. Axonal and dendritic collaterals inside the mini column form a structure suitable for the appearance of selected sites.

A rough estimate of how much memory a single mini-column can store can be made from the following considerations. The amount of information in one description is approximately determined by the capacity of the binary code arising from the activity of the dendritic sections of the minicolumn. The total number of N _ds dendritic sections in the minicolumn is approximately 100 * 30 = 3000 (both the dendrites of the neuron's own neurons and the dendrites of the neurons of the neighboring minicolumns) fall into the minicolumn. If we assume that a complex description encodes the activity of N _sig elements, then the amount of information in a single description by Shannon will be


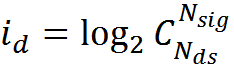
When N _sig = 150 this is 854 bits or about 100 bytes. To encode a single description, in the assumptions made, it is necessary to change the state of 150 receptive clusters. Thus, one cluster accounts for information


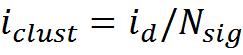
The amount of information per cluster does not strongly depend on N _sig (table below) and is about 6 bits.



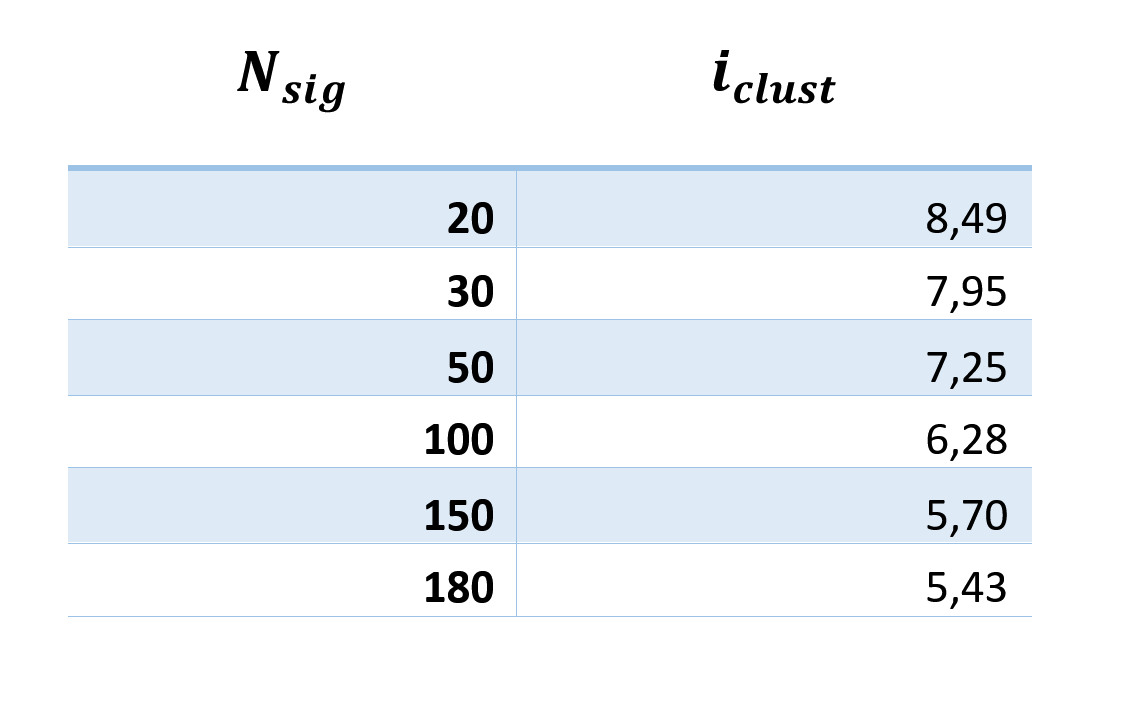
Thus, the information capacity of the minicolumn can be estimated


Where N _cl is the number of receptive clusters per synapse, N _syn is the number of synapses in one neuron (8000), N _neur is the number of neurons in the minicolon (100).

The number of receptors per synapse implies, in the main, the synapse surrounding extra-synaptic receptors. Potentially, their number may change over time. That is, hypothetically, the accumulation of memories may be accompanied by an increase in the total number of receptors.

Measuring the density of AMPA receptors in the synapse showed a value of 1600 receptors per square meter. um The diameter of the monomeric ATX receptor is 9 nm, the distance between the centers of the receptors in the dimer is 9.5 nm. On the surface of the spike and the adjacent dendrite surface, potentially, hundreds and thousands of receptors can freely accommodate.

In our approach, the maximum reasonable number of receptive clusters near the synapse is limited by the number of possible combinations of the activity of the surrounding neurotransmitter sources. With 15 sources, the choice of 5 active ones gives about 3000 possible combinations.

Based on the above, we take N _cl equal to 500, assuming that such a number of receptors can accumulate in the process of memorizing over the long years of life. Then the minicolumn memory capacity will be 2.3x10 ⁹ bits or approximately 300 megabytes. Or 3 million semantic memories informative, 100 bytes each.

The approach, based on the plasticity of synapses as the main memory element, gives a much more modest result. The minicolumn contains about 800,000 synapses. Even assuming that the synapse, by changing the level of plasticity, encodes several bits of information, it turns out that the value amounts to just hundreds of kilobytes. An increase in the memory capacity by three orders of magnitude gives a qualitative leap in the information capabilities of the mini-column. Since the information stored in the minicarrier has a nature that is close to semantic, 300 megabytes are enough to save, for example, all the memories of a person accumulating in the course of his life.

A book of 500 pages in uncompressed form takes about 500 kilobytes. Minicolumn allows you to store a library of memories, consisting of 600 volumes. Approximately according to that for a month of life or 15 pages for a day. It seems that this is quite enough to accommodate the semantic description of everything that happens to us.

Again, since each zone of the cortex has its own specialization, the minicolumns of each zone do not need to store totally the entire memory of our brain; they only need to have a memory about their subject matter.

Three hundred megabytes of mini-column memory should not be compared with the gigabyte size of photographic libraries or film libraries. It seems that when images are stored in memory, they are not stored in a photographic form, but in the form of short semantic descriptions consisting of concepts corresponding to the image. At the moment of memory, the image is not reproduced, but reconstructed again, creating the illusion of photographic memory. This can be compared with the fact that a portrait of a person can be restored sufficiently close to a photograph only by his verbal description.

The actual memory of a minicolumn can be several times higher if we assume that the receptors of the glial cells of the cortex are also carriers of the information code. For contextual computing modules, two main types of memory are required: the memory of past interpretations and the memory of transformation rules. It is possible that these types of memory are divided between neurons and plasma astrocytes.

At first, the idea that only 100 neurons of a minicolon can store memories of a lifetime seems absurd, especially for those who are used to thinking that memory is distributed throughout the entire space of the cortex. , . .

, , ( ). . , , , . , . . , , . – , , , .




, , . , , . .

. , . , – , .

, , , , .

, , , . , .
. , , - , .

, , , . . , , « – » « – ».

. , , . - . , . . , , .

, . . , . , , – .

, , .

, , , , .
, , . , , .

, «» , , . - . . . , , , «», . . - , , .

, , . , , . , — , . . , — .

Another example. . , , , .

- , , - . , , .

. , , , , , - , . , .

, . . .

, , , , . . , . , , .

, , . . , , , -, . . -, , . -, . , 150 , .

, , , . 300 , .

, . , . .

Alexey Redozubov

PS . ( — ). . , . . , .

The logic of consciousness. Introduction
The logic of consciousness. Part 1. Waves in the cellular automaton
The logic of consciousness. Part 2. Dendritic waves
The logic of consciousness. Part 3. Holographic memory in a cellular automaton
The logic of consciousness. Part 4. The secret of brain memory
The logic of consciousness. Part 5. The semantic approach to the analysis of information
The logic of consciousness. Part 6. The cerebral cortex as a space for calculating meanings.
The logic of consciousness. Part 7. Self-organization of the context space

The logic of consciousness. Explanation "on the fingers"
The logic of consciousness. Part 8. Spatial maps of the cerebral cortex
The logic of consciousness. Part 9. Artificial neural networks and minicolumns of the real cortex.
The logic of consciousness. Part 10. The task of generalization
The logic of consciousness. Part 11. Natural coding of visual and sound information
The logic of consciousness. Part 12. The search for patterns. Combinatorial space