Why it is not necessary to blame the inaccuracy of O-ratings for their problems

The recent publication of this and now this translation inspired me to write this post, in which the authors express their dissatisfaction in an intelligent way about how O-estimates of the computational complexity of classical, seemingly, algorithms entered into dissonance with their practical development experience. The main subject of criticism was the memory model, in which these estimates were obtained - it, de, does not take into account the peculiarities of hierarchical organization according to the principle of speed, which takes place in modern computing systems. From what all subsequent troubles grow. And judging by the observed reaction of grateful readers, the authors are far from being alone in their indignation and in their desire to “overlap” the classics with their O-big ones. So perhaps it is really worth sending to the dustbin the history of the display of uncles in white coats, made by them for tube-breathing and heat-breathing machines, and to give way to young ambitious models that more accurately reflect the anatomy of modern iron?


Let's understand

In the course of the text, I will refer to the second publication and some comments on it. Touched for a living. But for a start, let's agree exactly what is meant by this text.

We introduce the definition. Let be and - two real functions defined on the set . Then write means that there is such a positive number that for all fair . This designation is called -notation, and O is called the Bachmann symbol, or simply " O- big".
')
From this definition there are several consequences at once:

1. If for all takes place then from " follows that . In particular, we have that multiplication by a constant does not change the O- estimate.

Simply put, when multiplying an O- expression by a constant, the Bachmann symbol “eats” this constant. This means that an equal sign in an expression that includes an O -evaluation cannot be interpreted as a classical “equality” of values, and mathematical expressions cannot be applied to such expressions without further clarification . Otherwise we would get weird things like the following: . This is a consequence of the arbitrariness of a constant that “hides” behind the Bachmann symbol.

2. If limited to there is such a number that for all performed then .

Translating from mathematical to Russian and taking for simplicity as the finite interval of the number line, we have the following: if the function at a given interval does not go to infinity, then the most senseless thing to say about it is that it corresponds to O (1). This is absolutely nothing new to say about her behavior .


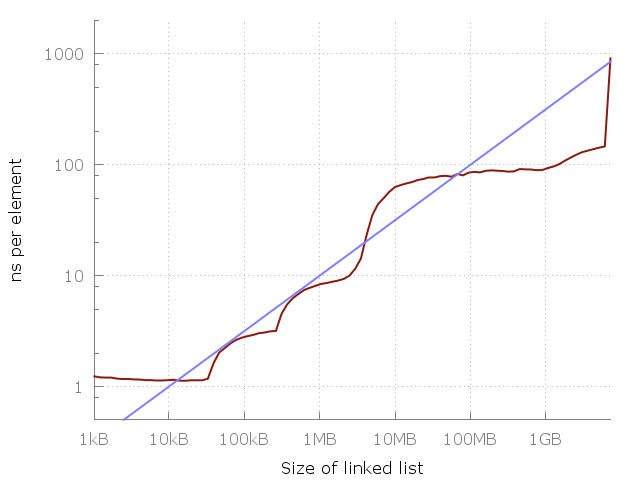
The blue line is O (√N).

Let us return to the case of estimating the complexity of the algorithm and look at the picture given by the author of the cited publication. Observing the increase in execution time, it is concluded that the O (1) estimate is inconsistent. But the interval at which the behavior of the program is analyzed is finite. So, in fact, it is claimed that the O (1) estimate on it is bad.

Well ... thanks, cap.

Moreover, an attempt is further made to guess ! the majorizing function is simply by the form of a curve, they say, "as much as it seems." Without conducting any analysis of the algorithm itself, taking into account the features that are trying to focus attention and not introducing any memory model! And why, actually, is the square root there, and not cubic? Or not a logarithm of any stray? Well, the right word, would offer at least a couple of options, why did the "attention, correct answer" immediately?

It is worth making a reservation. Naturally, I do not lead to the incorrect conclusion that during the transition to the “farther” from the processor, the access time drops. But the time of receiving a portion of data with random access to memory even at the slowest level of the hierarchy is a constant or at least limited value. From which the estimate O (1) follows. And if it is not limited and depends on the dimension of the data, then memory access is not arbitrary. Well, stupid by definition . Let's not forget that we are dealing with idealized algorithmic constructions. Therefore, when it is said that “data centers will go further behind HDD” ... Gentlemen, well, what kind of random access is this, what arrays and hash tables? This is called under the table: you quietly change the conditions of the problem, bring the answer to the previous one and shout: “Achtung! Wrong as! ". It causes an attack of heavy bewilderment in me. After all, if behind the word array , vector or <some-type> * your compiler hides, say, a piece of memory distributed over the nodes of a cluster - then this structure can be anything, but not an array in terms of the books of Wirth and Knuth, and apply to them the results of formal analysis written in these books are a highly stupid idea. And no less schizophrenia - quite seriously talking about the generality of the assessment, invented looking at the graph with the results of an arbitrary test.

The fallacy of the given judgment is that the O- estimation of complexity is made on the basis of an experiment. To emphasize this, we introduce another “property” of O -notations applicable to estimates of algorithmic complexity:

3. O -estimation can be obtained only from the analysis of the structure of the algorithm, but not from the results of the experiment. According to the results of the experiment, you can get statistical estimates, expert estimates, approximate estimates and, finally, engineering and aesthetic pleasure - but not asymptotic estimates.

The latter is a consequence of the fact that the very meaning of such estimates is to get an idea of ​​the behavior of the algorithm with sufficiently large data dimensions, and how large it is usually not specified. This is not the only and far from always main, but interesting characteristic of the algorithm. At the time of Dijkstra and Hoar, the orders of dimension 3-6 could be considered rather large, nowadays 10-100 (according to my estimates that do not pretend to the depth of analysis). In other words, when raising the question of obtaining asymptotic estimates for the complexity function of an algorithm, it is convenient to modify the definition of O -notation as follows:

Let be . Then means that there are mutually independent positive numbers A and n , such that for all performed .

That is, when analyzing algorithmic complexity, we actually consider the majorant functions of complexity on all intervals that are left bounded and not right bounded. Therefore, such O -evaluations can be specified arbitrarily many, and all such evaluations can be practically useful. Some of them will be accurate for small N , but quickly go to infinity. Others will grow slowly, but will become fair starting from the N , to which we walk on our poor computers as far as the Moon. So if we assume that the assessment of memory access time If any structural analysis is hidden, then this estimate could well be used in a certain range of dimensions, but even then it would not cancel the correctness of the O (1) estimate.

A classic example of incorrect comparison of asymptotic estimates is the multiplication algorithms of square matrices. If you make a choice between algorithms only on the basis of a comparison of estimates, then we take the Williams algorithm and do not steam. We can only wish the creative success of the decision maker to apply it to matrices of dimensions that are characteristic of engineering problems. But on the other hand, we know that, starting with a certain dimension of the problem, the Strassen algorithm and its various modifications will work faster than the trivial, and this gives us room for maneuver in choosing approaches to solving the problem.

How stupidity comes out of wisdom

To sin on the inaccuracy of the O- scores is to not fully understand the meaning of these estimates, and if this is so, then no one forces them to use them. It is quite possible and often justified to prefer them statistical estimates obtained as a result of tests on specific data sets specifically for your area. Illiterate use of such a delicate instrument as asymptotic analysis leads to kinks and generally surprising pieces. For example, using the O- notation, it is possible to prove the inconsistency of the idea of ​​parallel programming.

Suppose that our algorithm, which is fed a portion of data of dimension N and which, when executed sequentially, has complexity , is easily and naturally divided into the same N independent and, for simplicity, parts of the same computational and temporal complexity. We get that the complexity of each such part is . Suppose we have M independent solvers. Then the overall complexity of the execution of the parallel algorithm is nothing more than . It turned out that the asymptotic estimate of the complexity of the algorithm as a result of even perfect parallelization to a finite number of processes does not change. But the attentive reader noticed that the “hidden” constant had changed, which had been crammed with the Bachmann symbol. That is, it is at least silly to draw from such an analysis any general conclusions regarding the very idea of ​​parallelization. But another extreme is also possible - to forget that the number of processors is of course and based on the infinite resource of parallelism to assert that the estimate of the “parallel version of the algorithm” is O (1).

Let's sum up

As a conclusion, you can provide the following novelty assertions:

• It cannot be argued that one algorithm is more efficient than another on the basis of a simple comparison of their O- scores. Such a statement always requires clarification.
  
  
• It is impossible to conclude from the results of performance measurements whether these estimates are correct or incorrect - the hidden constant is usually unknown and can be quite large.
  
  
• It is possible (and sometimes necessary) to reason about algorithms and data structures without using such estimates at all. To do this, it is enough just to say exactly what their properties interest you.
  
  
• But it is better to take specific engineering solutions, including the characteristics of the algorithms used.

Behind the statement that the asymptotic estimates are inaccurate, incorrect or impractical, there is often a reluctance to conduct a normal preliminary analysis of the problem posed and an attempt to rely on the name, but not the essence of the abstractions that are dealt with. Speaking about the asymptotic complexity of the algorithm, a competent specialist understands that we are talking about idealized structures, keeps in mind the degree of correctness of projecting them onto real hardware, and never , from the word “in general,” makes engineering decisions relying solely on it. O- evaluations are more useful in developing new algorithms and finding fundamental solutions to complex problems and are much less useful in writing and debugging specific programs for specific hardware. But if you interpreted them incorrectly and received something completely different from what your reading comprehension promised in smart books, you will agree that this is not a problem for those who have received these evaluations conclusively.