Analytical calculation of derivatives on C ++ templates
A few days ago they wrote about analytic finding of derivatives, which reminded me of one of my small C ++ libraries, which does almost the same thing, but at compile time.
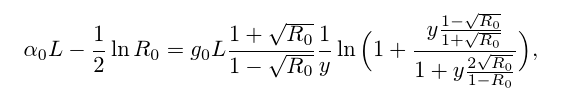
What is the profit? The answer is simple: I had to set the minimum to find a fairly complex function, consider the derivatives of this function to be a pen on paper for laziness, check later that I was not sealed when writing the code, and support this same code - it is doubly lazy, so it was decided to write the thing that does it for me. Well, in order to write something like this in the code:
Instead of crocodiles, which are obtained if we take the partial derivatives of the functions in the picture at the beginning (or rather, some simplified version of it, but it doesn’t look so bad).
')
It's also nice to be confident enough that the compiler is optimizing it as if the corresponding derivatives and functions were written by hand. And I would like to be sure - it was necessary to find the minimum many times (indeed, many, from hundreds of millions to billions, this was the essence of some kind of computational experiment), so the calculation of the derivatives would be a bottleneck any recursion on a tree structure. If we force the compiler to calculate the derivative, in fact, at compile time, then there is a chance that it will still be passed by the optimizer according to the resulting code, and we will not lose compared to manual writing all the derivatives. The chance came true, by the way.
Under the cut - a small description of how it all works there.
Let's start with the presentation of the function in the program. For some reason, it turned out that every function is a type. A function is also an expression tree, and the node of this tree is represented by the
Here
Nodes are able to differentiate themselves, to print and calculate for given values of free variables and parameters. So, if a type is defined for representing a node with a regular number:
then the knot specialization for numbers is trivial:
The derivative of any number with respect to any variable is zero (the type
The variable appears in a similar way:
Here, they will be equal to
they will be equal to  -
-
The node for a variable is defined a little more interesting than for a number:
Thus, the derivative of a variable is equal to one by itself, and zero for any other variable. Actually, the
Calculating the value of a function consisting of one variable is reduced to finding it in the value
With unary functions, everything becomes more interesting.
In the
Then the node itself looks like this:
We consider the derivative through the chain rule - it looks scary, the idea is simple. The calculation is also simple: we count the value of the child node, then we calculate the value of our unary function on this value using the
By the way, a separate unary operation of negation could not be introduced, replacing it with multiplication by minus one.
With binary nodes, everything is the same, only derivatives look absolutely scary. For division, for example:
Then the required
If we now define auxiliary variables and types, for example:
then you can write the code just like at the very beginning of the post.
What is left?
First, deal with the type that is passed to the
Motivation (you can skip): if you slightly profile the code that comes out of the current version, it will catch your eye, which takes quite a long time to calculate which, generally speaking, is the same for each experimental point. No problem! We introduce a separate variable, which we calculate once before calculating the values of our formula at each of the experimental points, and replace all occurrences
which, generally speaking, is the same for each experimental point. No problem! We introduce a separate variable, which we calculate once before calculating the values of our formula at each of the experimental points, and replace all occurrences  to this variable (in fact, in the motivation code at the very beginning, this has already been done). However, when we take the derivative with respect to
to this variable (in fact, in the motivation code at the very beginning, this has already been done). However, when we take the derivative with respect to  we will have to remember that
we will have to remember that  , generally speaking, not a free parameter, but a function of
, generally speaking, not a free parameter, but a function of  . Recall is very simple: replace
. Recall is very simple: replace  on
on  (
(  on
on  back:
back:
The implementation is verbose, but ideologically simple. Recursively descend the formula tree, replacing an element of the tree, if it exactly matches the template, otherwise we change nothing. Total three specializations: for descending a child node of a unary function, for descending a child nodes of a binary function, and for a replacement itself, while specializations for descending a child nodes should check that the pattern does not match the subtree corresponding to the subfunction in question:
Ffuh. It remains to understand the transfer of parameter values.
Recall that each parameter has its own type, so if we build a family of functions, overloaded with the type of parameters, each of which returns the corresponding value, then again (just like with the calculation of unary functions a little earlier) there is a chance that the compiler will turn this thing and he is optimizing (by the way, he is optimizing, such a clever girl). Well, something like:
Only we want to make it beautiful so that you can write, for example:
where
How can we cross a hedgehog and a hedgehog, having made a function in general, the type of the parameter of which is set in compile-time and the value in runtime? Lambdas rush to the rescue!
Suppose we have two such functions, how can we get a family of functions in the same namespace so that the desired one is chosen by overloading? Inheritance to the rescue!
We inherit from both lambdas (after all, lambda expands into a structure with a name generated by the compiler, which means that we can inherit from it) and bring their round-brackets to the script.
Moreover, it is possible to inherit not only from lambdas, but also from arbitrary structures that have some round-bracket operators.Oops, got algebra. Thus, if there are N lambdas, you can inherit the first
Automatically we get the completeness and uniqueness: if some arguments are not given, it will be a compilation error, as well as if some arguments are given twice.
Actually, everything.
Unless, one of my friends, to whom I showed it at one time, offered, in my opinion, a more elegant solution on constexpr-functions, but I haven't reached my hand for 9 months already.
Well, the link to the library: I Am Mad . Not ready for production, pull-walks are accepted, and so on.
Well, you can still wonder how clever modern compilers can wipe through all these layers of templates over templates over lambdas over templates and generate a fairly optimal code.
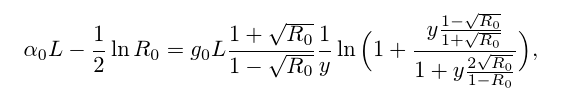
What is the profit? The answer is simple: I had to set the minimum to find a fairly complex function, consider the derivatives of this function to be a pen on paper for laziness, check later that I was not sealed when writing the code, and support this same code - it is doubly lazy, so it was decided to write the thing that does it for me. Well, in order to write something like this in the code:
using Formula_t = decltype (k * (_1 - r0) / (_1 + r0) * (g0 / (alpha0 - logr0 / Num<300>) - _1)); // const auto residual = Formula_t::Eval (datapoint) - knownValue; // // : const auto dg0 = VarDerivative_t<Formula_t, decltype (g0)>::Eval (datapoint); const auto dalpha0 = VarDerivative_t<Formula_t, decltype (alpha0)>::Eval (datapoint); const auto dk = VarDerivative_t<Formula_t, decltype (k)>::Eval (datapoint); Instead of crocodiles, which are obtained if we take the partial derivatives of the functions in the picture at the beginning (or rather, some simplified version of it, but it doesn’t look so bad).
')
It's also nice to be confident enough that the compiler is optimizing it as if the corresponding derivatives and functions were written by hand. And I would like to be sure - it was necessary to find the minimum many times (indeed, many, from hundreds of millions to billions, this was the essence of some kind of computational experiment), so the calculation of the derivatives would be a bottleneck any recursion on a tree structure. If we force the compiler to calculate the derivative, in fact, at compile time, then there is a chance that it will still be passed by the optimizer according to the resulting code, and we will not lose compared to manual writing all the derivatives. The chance came true, by the way.
Under the cut - a small description of how it all works there.
Let's start with the presentation of the function in the program. For some reason, it turned out that every function is a type. A function is also an expression tree, and the node of this tree is represented by the
Node type: template<typename NodeClass, typename... Args> struct Node; Here
NodeClass is the node type (variable, number, unary function, binary function), Args are the parameters of this node (variable index, value of number, child nodes).Nodes are able to differentiate themselves, to print and calculate for given values of free variables and parameters. So, if a type is defined for representing a node with a regular number:
using NumberType_t = long long; template<NumberType_t N> struct Number {}; then the knot specialization for numbers is trivial:
template<NumberType_t N> struct Node<Number<N>> { template<char FPrime, int IPrime> using Derivative_t = Node<Number<0>>; static std::string Print () { return std::to_string (N); } template<typename Vec> static typename Vec::value_type Eval (const Vec&) { return N; } constexpr Node () {} }; The derivative of any number with respect to any variable is zero (the type
Derivative_t is responsible for this, let’s leave its template parameters for now). Printing a number is also easy (see Print() ). Calculate a node with a number — return this number (see Eval() , the Vec template parameter will be discussed later).The variable appears in a similar way:
template<char Family, int Index> struct Variable {}; Here,
Family and Index are the “family” and variable index. So for  they will be equal to
they will be equal to 'w' and 1 , and for  -
- 'x' and 2 respectively.The node for a variable is defined a little more interesting than for a number:
template<char Family, int Index> struct Node<Variable<Family, Index>> { template<char FPrime, int IPrime> using Derivative_t = std::conditional_t<FPrime == Family && IPrime == Index, Node<Number<1>>, Node<Number<0>>>; static std::string Print () { return std::string { Family, '_' } + std::to_string (Index); } template<typename Vec> static typename Vec::value_type Eval (const Vec& values) { return values (Node {}); } constexpr Node () {} }; Thus, the derivative of a variable is equal to one by itself, and zero for any other variable. Actually, the
FPrime and IPrime for the type Derivative_t are the family and the index of the variable on which you want to take the derivative.Calculating the value of a function consisting of one variable is reduced to finding it in the value
values dictionary, which is passed to the Eval() function. The dictionary itself is able to find the value of the desired variable by its type, so we will simply give it the type of our variable and return the corresponding value. As a dictionary it does, we will look at it later.With unary functions, everything becomes more interesting.
enum class UnaryFunction { Sin, Cos, Ln, Neg }; template<UnaryFunction UF> struct UnaryFunctionWrapper; In the
UnaryFunctionWrapper specialization UnaryFunctionWrapper we stuff the logic by taking the derivatives of each specific unary function. To minimize duplicate code, we will take the derivative of the unary function by its argument, the caller will answer for further differentiation of the argument by the target variable through the chain rule: template<> struct UnaryFunctionWrapper<UnaryFunction::Sin> { template<typename Child> using Derivative_t = Node<Cos, Child>; }; template<> struct UnaryFunctionWrapper<UnaryFunction::Cos> { template<typename Child> using Derivative_t = Node<Neg, Node<Sin, Child>>; }; template<> struct UnaryFunctionWrapper<UnaryFunction::Ln> { template<typename Child> using Derivative_t = Node<Div, Node<Number<1>>, Child>; }; template<> struct UnaryFunctionWrapper<UnaryFunction::Neg> { template<typename> using Derivative_t = Node<Number<-1>>; }; Then the node itself looks like this:
template<UnaryFunction UF, typename... ChildArgs> struct Node<UnaryFunctionWrapper<UF>, Node<ChildArgs...>> { using Child_t = Node<ChildArgs...>; template<char FPrime, int IPrime> using Derivative_t = Node<Mul, typename UnaryFunctionWrapper<UF>::template Derivative_t<Child_t>, typename Node<ChildArgs...>::template Derivative_t<FPrime, IPrime>>; static std::string Print () { return FunctionName (UF) + "(" + Node<ChildArgs...>::Print () + ")"; } template<typename Vec> static typename Vec::value_type Eval (const Vec& values) { const auto child = Child_t::Eval (values); return EvalUnary (UnaryFunctionWrapper<UF> {}, child); } }; We consider the derivative through the chain rule - it looks scary, the idea is simple. The calculation is also simple: we count the value of the child node, then we calculate the value of our unary function on this value using the
EvalUnary() function. Rather, a family of functions: the first argument of the function is the type that defines our unary function, to ensure the choice of the desired overload during compilation. Yes, one could pass the UF value itself, and a smart compiler would almost certainly make all the necessary constant propagation passes, but here it’s easier to be safe.By the way, a separate unary operation of negation could not be introduced, replacing it with multiplication by minus one.
With binary nodes, everything is the same, only derivatives look absolutely scary. For division, for example:
template<> struct BinaryFunctionWrapper<BinaryFunction::Div> { template<char Family, int Index, typename U, typename V> using Derivative_t = Node<Div, Node<Add, Node<Mul, typename U::template Derivative_t<Family, Index>, V >, Node<Neg, Node<Mul, U, typename V::template Derivative_t<Family, Index> > > >, Node<Mul, V, V > >; }; Then the required
VarDerivative_t is determined quite simply, because in fact it only calls Derivative_t on the node passed to it: template<typename Node, typename Var> struct VarDerivative; template<typename Expr, char Family, int Index> struct VarDerivative<Expr, Node<Variable<Family, Index>>> { using Result_t = typename Expr::template Derivative_t<Family, Index>; }; template<typename Node, typename Var> using VarDerivative_t = typename VarDerivative<Node, std::decay_t<Var>>::Result_t; If we now define auxiliary variables and types, for example:
// : using Sin = UnaryFunctionWrapper<UnaryFunction::Sin>; using Cos = UnaryFunctionWrapper<UnaryFunction::Cos>; using Neg = UnaryFunctionWrapper<UnaryFunction::Neg>; using Ln = UnaryFunctionWrapper<UnaryFunction::Ln>; using Add = BinaryFunctionWrapper<BinaryFunction::Add>; using Mul = BinaryFunctionWrapper<BinaryFunction::Mul>; using Div = BinaryFunctionWrapper<BinaryFunction::Div>; using Pow = BinaryFunctionWrapper<BinaryFunction::Pow>; // variable template C++14 : template<char Family, int Index = 0> constexpr Node<Variable<Family, Index>> Var {}; // x0 , , : using X0 = Node<Variable<'x', 0>>; constexpr X0 x0; // // , : constexpr Node<Number<1>> _1; // , , : template<typename T1, typename T2> Node<Add, std::decay_t<T1>, std::decay_t<T2>> operator+ (T1, T2); template<typename T1, typename T2> Node<Mul, std::decay_t<T1>, std::decay_t<T2>> operator* (T1, T2); template<typename T1, typename T2> Node<Div, std::decay_t<T1>, std::decay_t<T2>> operator/ (T1, T2); template<typename T1, typename T2> Node<Add, std::decay_t<T1>, Node<Neg, std::decay_t<T2>>> operator- (T1, T2); // , : template<typename T> Node<Sin, std::decay_t<T>> Sin (T); template<typename T> Node<Cos, std::decay_t<T>> Cos (T); template<typename T> Node<Ln, std::decay_t<T>> Ln (T); then you can write the code just like at the very beginning of the post.
What is left?
First, deal with the type that is passed to the
Eval() function. Secondly, to mention the possibility of converting the desired expression with the replacement of one subtree with another. Let's start with the second, it's easier.Motivation (you can skip): if you slightly profile the code that comes out of the current version, it will catch your eye, which takes quite a long time to calculate
 which, generally speaking, is the same for each experimental point. No problem! We introduce a separate variable, which we calculate once before calculating the values of our formula at each of the experimental points, and replace all occurrences
which, generally speaking, is the same for each experimental point. No problem! We introduce a separate variable, which we calculate once before calculating the values of our formula at each of the experimental points, and replace all occurrences  to this variable (in fact, in the motivation code at the very beginning, this has already been done). However, when we take the derivative with respect to
to this variable (in fact, in the motivation code at the very beginning, this has already been done). However, when we take the derivative with respect to  we will have to remember that
we will have to remember that  , generally speaking, not a free parameter, but a function of
, generally speaking, not a free parameter, but a function of  . Recall is very simple: replace
. Recall is very simple: replace  on
on  (
( ApplyDependency_t metafunction is used for this, although it would be Rewrite_t correct to call it Rewrite_t or something like that), differentiate, return  on
on  back:
back: using Unwrapped_t = ApplyDependency_t<decltype (logr0), decltype (Ln (r0)), Formula_t>; using Derivative_t = VarDerivative_t<Unwrapped_t, decltype (r0)>; using CacheLog_t = ApplyDependency_t<decltype (Ln (r0)), decltype (logr0), Derivative_t>; The implementation is verbose, but ideologically simple. Recursively descend the formula tree, replacing an element of the tree, if it exactly matches the template, otherwise we change nothing. Total three specializations: for descending a child node of a unary function, for descending a child nodes of a binary function, and for a replacement itself, while specializations for descending a child nodes should check that the pattern does not match the subtree corresponding to the subfunction in question:
template<typename Var, typename Expr, typename Formula, typename Enable = void> struct ApplyDependency { using Result_t = Formula; }; template<typename Var, typename Expr, typename Formula> using ApplyDependency_t = typename ApplyDependency<std::decay_t<Var>, std::decay_t<Expr>, Formula>::Result_t; template<typename Var, typename Expr, UnaryFunction UF, typename Child> struct ApplyDependency<Var, Expr, Node<UnaryFunctionWrapper<UF>, Child>, std::enable_if_t<!std::is_same<Var, Node<UnaryFunctionWrapper<UF>, Child>>::value>> { using Result_t = Node< UnaryFunctionWrapper<UF>, ApplyDependency_t<Var, Expr, Child> >; }; template<typename Var, typename Expr, BinaryFunction BF, typename FirstNode, typename SecondNode> struct ApplyDependency<Var, Expr, Node<BinaryFunctionWrapper<BF>, FirstNode, SecondNode>, std::enable_if_t<!std::is_same<Var, Node<BinaryFunctionWrapper<BF>, FirstNode, SecondNode>>::value>> { using Result_t = Node< BinaryFunctionWrapper<BF>, ApplyDependency_t<Var, Expr, FirstNode>, ApplyDependency_t<Var, Expr, SecondNode> >; }; template<typename Var, typename Expr> struct ApplyDependency<Var, Expr, Var> { using Result_t = Expr; }; Ffuh. It remains to understand the transfer of parameter values.
Recall that each parameter has its own type, so if we build a family of functions, overloaded with the type of parameters, each of which returns the corresponding value, then again (just like with the calculation of unary functions a little earlier) there is a chance that the compiler will turn this thing and he is optimizing (by the way, he is optimizing, such a clever girl). Well, something like:
auto GetValue (Variable<'x', 0>) { return value_for_x0; } auto GetValue (Variable<'x', 1>) { return value_for_x1; } ... Only we want to make it beautiful so that you can write, for example:
BuildFunctor (g0, someValue, alpha0, anotherValue, k, yetOneMoreValue, r0, independentVariable, logr0, logOfTheIndependentVariable); where
g0 , alpha0 and company are objects that have the types of the corresponding variables, followed by the corresponding values.How can we cross a hedgehog and a hedgehog, having made a function in general, the type of the parameter of which is set in compile-time and the value in runtime? Lambdas rush to the rescue!
template<typename ValueType, typename NodeType> auto BuildFunctor (NodeType, ValueType val) { return [val] (NodeType) { return val; }; } Suppose we have two such functions, how can we get a family of functions in the same namespace so that the desired one is chosen by overloading? Inheritance to the rescue!
template<typename F, typename S> struct Map : F, S { using F::operator(); using S::operator(); Map (F f, S s) : F { std::forward<F> (f) } , S { std::forward<S> (s) } { } }; We inherit from both lambdas (after all, lambda expands into a structure with a name generated by the compiler, which means that we can inherit from it) and bring their round-brackets to the script.
Moreover, it is possible to inherit not only from lambdas, but also from arbitrary structures that have some round-bracket operators.
Map from the first two lambdas, the next Map from the first Map and the next lambda, and so on. Let's make it in the form of a code: template<typename F> auto Augment (F&& f) { return f; } template<typename F, typename S> auto Augment (F&& f, S&& s) { return Map<std::decay_t<F>, std::decay_t<S>> { f, s }; } template<typename ValueType> auto BuildFunctor () { struct { ValueType operator() () const { return {}; } using value_type = ValueType; } dummy; return dummy; } template<typename ValueType, typename NodeType, typename... Tail> auto BuildFunctor (NodeType, ValueType val, Tail&&... tail) { return detail::Augment ([val] (NodeType) { return val; }, BuildFunctor<ValueType> (std::forward<Tail> (tail)...)); } Automatically we get the completeness and uniqueness: if some arguments are not given, it will be a compilation error, as well as if some arguments are given twice.
Actually, everything.
Unless, one of my friends, to whom I showed it at one time, offered, in my opinion, a more elegant solution on constexpr-functions, but I haven't reached my hand for 9 months already.
Well, the link to the library: I Am Mad . Not ready for production, pull-walks are accepted, and so on.
Well, you can still wonder how clever modern compilers can wipe through all these layers of templates over templates over lambdas over templates and generate a fairly optimal code.
Source: https://habr.com/ru/post/310016/
All Articles