Application of nonlinear dynamics and Chaos theory to the task of developing a new audio data compression algorithm
In this publication, I would like to present a number of ideas and experience of practical implementation of an element of Chaos theory - a fractal transformation in a project to develop a new audio data compression algorithm.
What you won't find here:
What you find here:
')
I think that for most readers of this publication this task will seem strange. Usually, the concept of fractal is associated with beautiful pictures - the results of fractal transformations, also called fractal (or “strange”) attractors. However, a careful study of fractal transformations allows us to understand that fractals are not only beautiful images. Fractal transformations define the projections of elements in a closed set. Such sets can be colored points in 2.5 D space, a set of points on a 2 D plane, or a set of discrete samples of an audio stream in 1.5 D space.
I became interested in fractal transformations from the moment of writing my thesis for the degree of candidate of technical sciences. The topic of the thesis was - “Algorithms for reducing the computational complexity of fractal analysis in visual data processing systems”. The thesis was successfully defended and accepted for publication by LAP LAMBERT Academic Publishing. Sometimes I meet links to it on sites Amazon and Ozon .
I spent a lot of time studying both theoretical foundations and practical results of research of fractal transformations and found only two attempts to develop fractal transformations to the level of industrial standards:
However, these attempts did not lead to significant success. The reason for the failures was a significant computational complexity.
The construction of images based on fractal transformations does not represent mathematical complexity. The well-known fractal (fractal set) of Mandelbrot is constructed on the basis of the following transformation:
Z (n + 1) = Zn ^ 2 + C where n = 1, 2, 3, ...

Thus, a very complex visualization can be achieved with a very simple expression. This leads to the next question - is it possible to construct a real image through a fractal transformation? This question was resolved in the affirmative. More precisely, one can find such a fractal transformation, which is capable of constructing an image with distortions less than or equal to any predetermined value. This means that the generated image may differ from the original by an amount indistinguishable by the viewer due to the redundancy of the visual information of the image. Thus, fractal image encoding is a lossy image processing technology.
In the book, Amazon or Ozon, you can find exact proofs of the applicability of the fractal transformation to image processing problems — Michael Brunsley's Collage Theorem.
You may ask - how to perform fractal coding (or more precisely - fractal analysis)? The visualization of the Mandelbrot fractal set is quite impressive, but it was developed after many years of research. Attempting to find a suitable fractal transformation by simple enumeration is hopeless. The solution to this problem was proposed by Michael Brunsley and his graduate students (Michael Brunsley later founded Iterated Systems Incorporated). They proposed a block scheme of fractal transformation. From the point of view of performing fractal transformations, there are no differences in the applicability of fractal transformations to a set of points or to a set of blocks of points - partitioned iterated function systems (PIFS). Such a scheme is based on extracting a copy of points from one part of a set of points, applying transformations to a copy, and inserting the result into another part of the set — this distinguishes this approach from fractal transformations for individual points. PIFS scheme can be represented as follows:
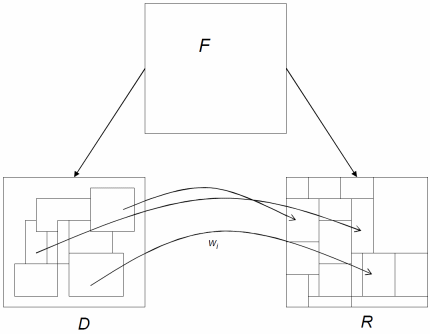
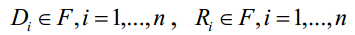
where F is the original set of points, D and R are sets of regions of points from F, - the transformation of one region from the set D and the region of the set R. Sets
- the transformation of one region from the set D and the region of the set R. Sets  and determine the desired fractal transformation. It is important to note that if the fractal transformation for the Mandelbrot fractal set is based on one equation of fractal transformation and the idea of global self-similarity (that is, the similarity of the entire set of any part of it), then the PIFS scheme is based on the group of fractal transformations and the idea of local similarity of individual regions of the set.
and determine the desired fractal transformation. It is important to note that if the fractal transformation for the Mandelbrot fractal set is based on one equation of fractal transformation and the idea of global self-similarity (that is, the similarity of the entire set of any part of it), then the PIFS scheme is based on the group of fractal transformations and the idea of local similarity of individual regions of the set.
You may ask - how does this relate to real images? On real images it is unlikely to find a global self-similarity, but it is possible to establish a similarity between different areas of the real image, subject to tolerance. If the resulting amount of memory for storing the system of equations of fractal transformations is less than the amount of memory for storing the original image, then a lossy image compression is obtained. This image processing approach is different from the classical idea of linear interpolation of signals.
To understand this difference, one needs to pay attention to three main properties of fractal transformations:
By analogy with the fractal transformation of the Mandelbrot set, the PIFS transformation for real images can be represented as follows:
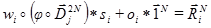
Where - transformation in the space of image points,
- transformation in the space of image points, 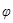 - compression vector transformation with a long
- compression vector transformation with a long 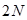 in vector with long
in vector with long 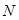 but what do variables mean
but what do variables mean 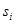 and
and 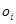 ? Variables
? Variables  and
and 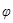 describe the transformation on the plane, but each point of the real image has a special meaning - the intensity of its own brightness, which should be considered as part of the fractal transformation space:
describe the transformation on the plane, but each point of the real image has a special meaning - the intensity of its own brightness, which should be considered as part of the fractal transformation space: 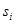 - compressive luminance conversion and
- compressive luminance conversion and 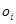 - the brightness intensity shift (by analogy with the straight line equation - f (y) = y * s + o).
- the brightness intensity shift (by analogy with the straight line equation - f (y) = y * s + o).
What to do with this equation? It is very simple - to execute this expression for all transformation groups ( ,
, 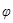 ,
, 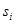 ,
, 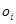 ) what should fill the set R, filling the whole image F. And once again, and again (recursive execution), to infinity. In reality, everything is much simpler - after each recursive iteration of the synthesis of a fractal set, the distance between the points decreases (the compressive property of the fractal transformation), but if for the analytical space there are no restrictions in divisibility, then for the discrete space of digital images the new points will fall into the cut-off space between neighboring samples. It will happen after
) what should fill the set R, filling the whole image F. And once again, and again (recursive execution), to infinity. In reality, everything is much simpler - after each recursive iteration of the synthesis of a fractal set, the distance between the points decreases (the compressive property of the fractal transformation), but if for the analytical space there are no restrictions in divisibility, then for the discrete space of digital images the new points will fall into the cut-off space between neighboring samples. It will happen after 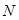 recursive PIFS iterations.
recursive PIFS iterations.
The expected question is how to find the coefficients mentioned. ,
, 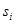 ,
, 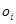 for a system of fractal transformations? The task of such a search can be automated based on the following equation:
for a system of fractal transformations? The task of such a search can be automated based on the following equation:
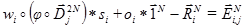
the search task is to find a pair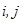 which minimizes the length of the vector of deviation
which minimizes the length of the vector of deviation 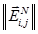 . If you set the extreme tolerance value to 0, you can derive the following approximations for
. If you set the extreme tolerance value to 0, you can derive the following approximations for 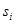 and
and 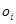 :
:
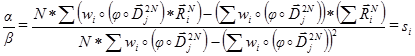
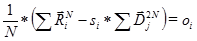
These expressions allow you to calculate the optimal values.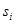 and
and 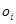 but unknown variables remain
but unknown variables remain  and couples
and couples 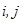 . Unfortunately, currently there are no analytical solutions for these variables - all that remains is to set the sets
. Unfortunately, currently there are no analytical solutions for these variables - all that remains is to set the sets  and steam
and steam 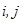 and sort through their combinations to minimize
and sort through their combinations to minimize 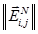 equations:
equations:
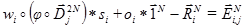
For effective minimization, it is required to set large ranges of values of the set and steam
and steam  , which leads to a “combinatorial explosion” - the need to enumerate hundreds of thousands of various combinations, which requires hours of operation of a computer processor. It is this problem that does not allow the transfer of fractal image analysis from the area of exotic research to the sphere of industrial standards.
, which leads to a “combinatorial explosion” - the need to enumerate hundreds of thousands of various combinations, which requires hours of operation of a computer processor. It is this problem that does not allow the transfer of fractal image analysis from the area of exotic research to the sphere of industrial standards.
I foresee a question - all the above described is interesting, but where does the sound and compression of sound data come from? I think many have already realized that for fractal analysis the nature of the sets does not matter - the set of pixels on the plane or the set of samples from the audio stream. If you accumulate samples of the input audio stream in the buffer and then process them as separate sets, you can form systems of fractal transformations from which you can synthesize fractal sets that are close to the original samples of the audio stream. This was implemented in my project, which includes the ROAD encoder and decoder (in the form of a plug-in for Winamp) - test audio files: Origa - Inner Universe 4Samples.road.wav and Alpha - Revolution in Paradise 4Samples.road.wav . A new algorithm for compressing audio data allowed developing a format with five unique properties:
Many mathematical concepts have physical interpretations. For example - and circle circumference or natural logarithm and spiral shell of the mollusk. Often indicate the relationship of fractal sets with the growth of crystals or trees. However, I would like to present my own interpretation of fractal transformations.
and circle circumference or natural logarithm and spiral shell of the mollusk. Often indicate the relationship of fractal sets with the growth of crystals or trees. However, I would like to present my own interpretation of fractal transformations.
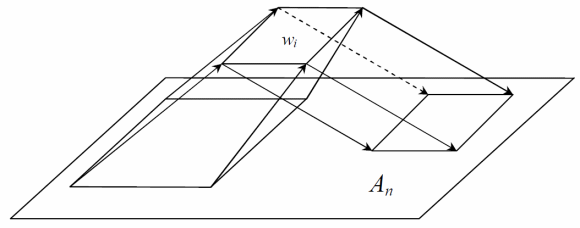
I propose to consider the basic expression of the PIFS fractal transform:
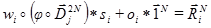
This expression can be represented as the following scheme:
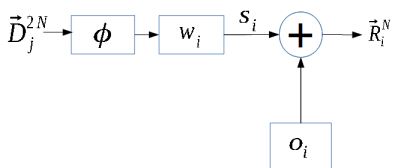
Taking into account the fact that the specified expression describes operations with vectors, consider the scheme of operations on each element of the vector:
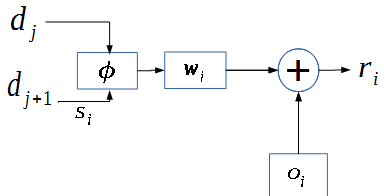
I believe that many readers will see the similarity of this scheme with the scheme of an artificial neuron:
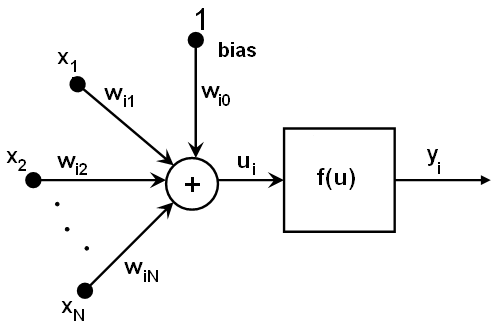
conversions and
and 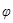 can be considered as a function of addition at the input,
can be considered as a function of addition at the input, 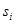 - sensitivity of an artificial neuron at the entrance,
- sensitivity of an artificial neuron at the entrance, 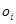 - the level of displacement - the excitation of an artificial neuron. An attentive reader may indicate that the sensitivity of an artificial neuron is determined for each input, while
- the level of displacement - the excitation of an artificial neuron. An attentive reader may indicate that the sensitivity of an artificial neuron is determined for each input, while 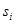 defined as a scalar for all inputs. Also, the reader will indicate the need for the output of the function to determine the state of an artificial neuron in terms of Binary (Boolean) logic: active or inactive. But are such requirements important? Is it acceptable that the sensitivity of an artificial neuron would be the same for all inputs? Yes, there are algorithms for learning artificial neural networks with a similar rule. Is a non-binary value valid at the output of an artificial neuron? At the beginning of the development of the theory of artificial neural networks, when the circuits were built on transistors, capacitors and resistors, they were required to solve simple problems from the field of recognition - for example, recognizing postal codes on postal envelopes and postcards using a perceptron. But with the development of fuzzy logic and the discovery of the advantages of “fuzzy decisions” (soft decisions) over “clear decisions” (hard decisions), the need for such a function can be questioned.
defined as a scalar for all inputs. Also, the reader will indicate the need for the output of the function to determine the state of an artificial neuron in terms of Binary (Boolean) logic: active or inactive. But are such requirements important? Is it acceptable that the sensitivity of an artificial neuron would be the same for all inputs? Yes, there are algorithms for learning artificial neural networks with a similar rule. Is a non-binary value valid at the output of an artificial neuron? At the beginning of the development of the theory of artificial neural networks, when the circuits were built on transistors, capacitors and resistors, they were required to solve simple problems from the field of recognition - for example, recognizing postal codes on postal envelopes and postcards using a perceptron. But with the development of fuzzy logic and the discovery of the advantages of “fuzzy decisions” (soft decisions) over “clear decisions” (hard decisions), the need for such a function can be questioned.
What happens if you look at fractal transformations from the point of view of the theory of artificial neural networks? Every element of the vector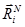 can be considered as one artificial neuron. In this case, the vector
can be considered as one artificial neuron. In this case, the vector 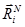 can be considered as a layer of artificial neurons with common properties. However, such “layers” can be several thousand for a small image. Plane transformation
can be considered as a layer of artificial neurons with common properties. However, such “layers” can be several thousand for a small image. Plane transformation  can be interpreted as a trace of connections between artificial neurons. An artificial neural network with linking-topology tracing between layers of artificial neurons for each individual task sounds very unusual, doesn't it? What features can such artificial neural networks have?
can be interpreted as a trace of connections between artificial neurons. An artificial neural network with linking-topology tracing between layers of artificial neurons for each individual task sounds very unusual, doesn't it? What features can such artificial neural networks have?
How can we call such an artificial neural network - a recursive, scalable, asynchronous, non-deterministic artificial neural network with a topology trace and a “soft” solution. An interesting fact is that there already exists an artificial neural network with similar properties - the Hopfield artificial neural network . This artificial Hopfield neural network is also recursive, also converges to a steady state and can be asynchronous. However, it includes one layer, does not include topology tracing, and does not form a “soft” solution. It is interesting that fractal transformations, like the Hopfield artificial neural network, have common filtering properties — recovery of damaged images (of course, fractal transformations can work with real images):



You can see that after removing several elements, fractal transformations can build an image close to the original after one iteration. However, the image “Rose”, which is very different from the original one, creates a very chaotic distribution of pixel intensity. This is consistent with the property of filtering - restoration of damaged images.
At this point you can finish this article. I hope the ideas expressed will turn your attention to the exotic area of fractal transformations.
What you won't find here:
- Complex equations. The purpose of this publication is to present the ideas and the vision of the problem. And like any other vision, it is largely abstract;
- Any generators of fractal images. Such images look interesting, but I am interested in real tasks.
What you find here:
')
- A brief overview of the application of fractal transformations to the problem of data lossy compression;
- Unusual interpretation of fractal transformations;
- References to real compressor code and audio data decompressor through fractal transformations (decompressor is presented in the form of a plug-in for the Winamp audio player);
- Description of the new format for storing compressed audio data with five unique properties that distinguish the new format from many well-known industrial audio formats.
I think that for most readers of this publication this task will seem strange. Usually, the concept of fractal is associated with beautiful pictures - the results of fractal transformations, also called fractal (or “strange”) attractors. However, a careful study of fractal transformations allows us to understand that fractals are not only beautiful images. Fractal transformations define the projections of elements in a closed set. Such sets can be colored points in 2.5 D space, a set of points on a 2 D plane, or a set of discrete samples of an audio stream in 1.5 D space.
I became interested in fractal transformations from the moment of writing my thesis for the degree of candidate of technical sciences. The topic of the thesis was - “Algorithms for reducing the computational complexity of fractal analysis in visual data processing systems”. The thesis was successfully defended and accepted for publication by LAP LAMBERT Academic Publishing. Sometimes I meet links to it on sites Amazon and Ozon .
I spent a lot of time studying both theoretical foundations and practical results of research of fractal transformations and found only two attempts to develop fractal transformations to the level of industrial standards:
- Video codec - 'ClearVideo' by company Iterated System Incorporated.
- Image / video codec - 'FIASCO' by Ullrich Hafner.
However, these attempts did not lead to significant success. The reason for the failures was a significant computational complexity.
Mathematical foundations
The construction of images based on fractal transformations does not represent mathematical complexity. The well-known fractal (fractal set) of Mandelbrot is constructed on the basis of the following transformation:
Z (n + 1) = Zn ^ 2 + C where n = 1, 2, 3, ...

Thus, a very complex visualization can be achieved with a very simple expression. This leads to the next question - is it possible to construct a real image through a fractal transformation? This question was resolved in the affirmative. More precisely, one can find such a fractal transformation, which is capable of constructing an image with distortions less than or equal to any predetermined value. This means that the generated image may differ from the original by an amount indistinguishable by the viewer due to the redundancy of the visual information of the image. Thus, fractal image encoding is a lossy image processing technology.
In the book, Amazon or Ozon, you can find exact proofs of the applicability of the fractal transformation to image processing problems — Michael Brunsley's Collage Theorem.
Pifs
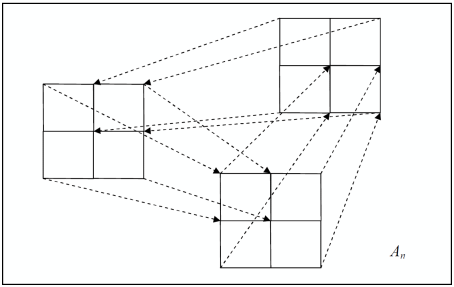
You may ask - how to perform fractal coding (or more precisely - fractal analysis)? The visualization of the Mandelbrot fractal set is quite impressive, but it was developed after many years of research. Attempting to find a suitable fractal transformation by simple enumeration is hopeless. The solution to this problem was proposed by Michael Brunsley and his graduate students (Michael Brunsley later founded Iterated Systems Incorporated). They proposed a block scheme of fractal transformation. From the point of view of performing fractal transformations, there are no differences in the applicability of fractal transformations to a set of points or to a set of blocks of points - partitioned iterated function systems (PIFS). Such a scheme is based on extracting a copy of points from one part of a set of points, applying transformations to a copy, and inserting the result into another part of the set — this distinguishes this approach from fractal transformations for individual points. PIFS scheme can be represented as follows:

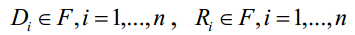
where F is the original set of points, D and R are sets of regions of points from F,
 - the transformation of one region from the set D and the region of the set R. Sets
- the transformation of one region from the set D and the region of the set R. Sets  and determine the desired fractal transformation. It is important to note that if the fractal transformation for the Mandelbrot fractal set is based on one equation of fractal transformation and the idea of global self-similarity (that is, the similarity of the entire set of any part of it), then the PIFS scheme is based on the group of fractal transformations and the idea of local similarity of individual regions of the set.
and determine the desired fractal transformation. It is important to note that if the fractal transformation for the Mandelbrot fractal set is based on one equation of fractal transformation and the idea of global self-similarity (that is, the similarity of the entire set of any part of it), then the PIFS scheme is based on the group of fractal transformations and the idea of local similarity of individual regions of the set.You may ask - how does this relate to real images? On real images it is unlikely to find a global self-similarity, but it is possible to establish a similarity between different areas of the real image, subject to tolerance. If the resulting amount of memory for storing the system of equations of fractal transformations is less than the amount of memory for storing the original image, then a lossy image compression is obtained. This image processing approach is different from the classical idea of linear interpolation of signals.
To understand this difference, one needs to pay attention to three main properties of fractal transformations:
- fractal transformation is recursive - it is based on the idea of unrestricted application of this transformation to the set;
- fractal transformation is compressive - this means the result is always less than the original;
- The space of fractal transformation is compact - all transformations over a set are reflected on the set itself (self-similarity).
By analogy with the fractal transformation of the Mandelbrot set, the PIFS transformation for real images can be represented as follows:
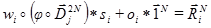
Where
 - transformation in the space of image points,
- transformation in the space of image points, 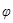 - compression vector transformation with a long
- compression vector transformation with a long 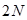 in vector with long
in vector with long 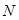 but what do variables mean
but what do variables mean 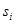 and
and 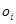 ? Variables
? Variables  and
and 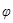 describe the transformation on the plane, but each point of the real image has a special meaning - the intensity of its own brightness, which should be considered as part of the fractal transformation space:
describe the transformation on the plane, but each point of the real image has a special meaning - the intensity of its own brightness, which should be considered as part of the fractal transformation space: 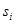 - compressive luminance conversion and
- compressive luminance conversion and 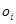 - the brightness intensity shift (by analogy with the straight line equation - f (y) = y * s + o).
- the brightness intensity shift (by analogy with the straight line equation - f (y) = y * s + o).What to do with this equation? It is very simple - to execute this expression for all transformation groups (
 ,
, 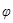 ,
, 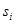 ,
, 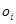 ) what should fill the set R, filling the whole image F. And once again, and again (recursive execution), to infinity. In reality, everything is much simpler - after each recursive iteration of the synthesis of a fractal set, the distance between the points decreases (the compressive property of the fractal transformation), but if for the analytical space there are no restrictions in divisibility, then for the discrete space of digital images the new points will fall into the cut-off space between neighboring samples. It will happen after
) what should fill the set R, filling the whole image F. And once again, and again (recursive execution), to infinity. In reality, everything is much simpler - after each recursive iteration of the synthesis of a fractal set, the distance between the points decreases (the compressive property of the fractal transformation), but if for the analytical space there are no restrictions in divisibility, then for the discrete space of digital images the new points will fall into the cut-off space between neighboring samples. It will happen after 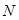 recursive PIFS iterations.
recursive PIFS iterations.The expected question is how to find the coefficients mentioned.
 ,
, 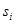 ,
, 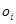 for a system of fractal transformations? The task of such a search can be automated based on the following equation:
for a system of fractal transformations? The task of such a search can be automated based on the following equation: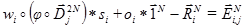
the search task is to find a pair
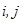 which minimizes the length of the vector of deviation
which minimizes the length of the vector of deviation 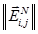 . If you set the extreme tolerance value to 0, you can derive the following approximations for
. If you set the extreme tolerance value to 0, you can derive the following approximations for 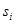 and
and 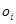 :
: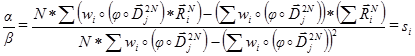
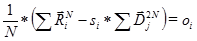
These expressions allow you to calculate the optimal values.
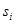 and
and 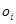 but unknown variables remain
but unknown variables remain  and couples
and couples 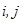 . Unfortunately, currently there are no analytical solutions for these variables - all that remains is to set the sets
. Unfortunately, currently there are no analytical solutions for these variables - all that remains is to set the sets  and steam
and steam 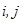 and sort through their combinations to minimize
and sort through their combinations to minimize 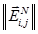 equations:
equations: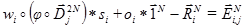
For effective minimization, it is required to set large ranges of values of the set
 and steam
and steam 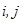 , which leads to a “combinatorial explosion” - the need to enumerate hundreds of thousands of various combinations, which requires hours of operation of a computer processor. It is this problem that does not allow the transfer of fractal image analysis from the area of exotic research to the sphere of industrial standards.
, which leads to a “combinatorial explosion” - the need to enumerate hundreds of thousands of various combinations, which requires hours of operation of a computer processor. It is this problem that does not allow the transfer of fractal image analysis from the area of exotic research to the sphere of industrial standards.Audio
I foresee a question - all the above described is interesting, but where does the sound and compression of sound data come from? I think many have already realized that for fractal analysis the nature of the sets does not matter - the set of pixels on the plane or the set of samples from the audio stream. If you accumulate samples of the input audio stream in the buffer and then process them as separate sets, you can form systems of fractal transformations from which you can synthesize fractal sets that are close to the original samples of the audio stream. This was implemented in my project, which includes the ROAD encoder and decoder (in the form of a plug-in for Winamp) - test audio files: Origa - Inner Universe 4Samples.road.wav and Alpha - Revolution in Paradise 4Samples.road.wav . A new algorithm for compressing audio data allowed developing a format with five unique properties:
- Pre-listening. This term sounds strange, but I decided to use it by analogy with the term “Preview” from the description of the JPEG2000 image compression format. But what does this mean for an audio file? If you look at the expression for calculating the coefficient
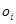 , it can be seen that it is calculated on the basis of averaging the values of neighboring samples. As a result, through the substitution, you can get the following expression:
, it can be seen that it is calculated on the basis of averaging the values of neighboring samples. As a result, through the substitution, you can get the following expression: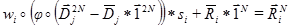
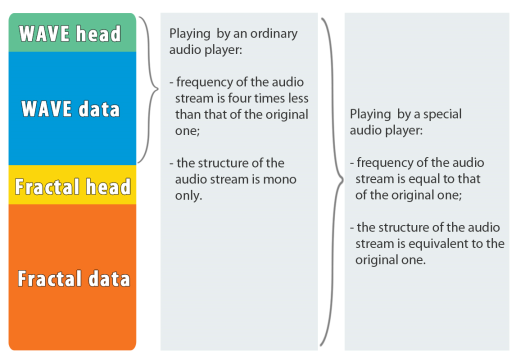
This expression shows an important fact - part of the coefficients of fractal transformations can be viewed as the average value of the image pixels or samples of the audio stream. This value is the “growth point” of the fractal set. Fractal transformations need similar points. However, when using PIFS for analyzing audio data, you can limit the size of the 4-point – sample regions - this allows you to get an average audio stream in the low-frequency region (for example, for the original audio stream frequency of 48000 Hz, the average stream has a frequency of 12000 Hz). As a result, the compressed stream can be listened to with degraded quality without decoding. I believe that this property can be defined as “Pre-listening”. - Partial compatibility. From the possibility of organizing a separate low-frequency stream of audio data from the coefficients of fractal transformations, the question arises - how to implement this? It is possible to reserve a separate section of the data stream, but the fact that this stream is an uncompressed data stream leads to the idea that this stream can be additionally compressed by another algorithm and packaged in a known industrial format. In this case, the file can be played in an audio player that is compatible with an industrial format with degraded quality. This idea can be implemented in the form of a stack of compressors. In my project, the WAVE format from Microsoft was selected. This format does not include compression, but allows in practice to implement a format stack and partial compatibility:
- Overclocking The idea of this property is to increase the frequency of the decoded audio stream. You can understand the idea of implementing this property if you consider why this property cannot be implemented in many industrial formats. For example, consider the mp3 format — when you try to double the frequency of a decoded audio stream, you need to increase the basis of the inverse discrete cosine transform from 128 to 256, but the compressed data only includes data for 128. This leads to the problem of incomplete orthogonal transform basis. A similar problem arises with linear prediction based formats. However, for fractal analysis, the situation is different. The coefficients considered earlier
 ,
, 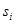 ,
, 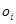 not related to the size of the basis of transformation:
not related to the size of the basis of transformation: 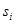 and
and 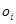 - intensity scalars,
- intensity scalars,  - transformation in space - displacement, reflection, etc ... A close analogy is raster and vector image formats: if raster formats assume the presence of one approximating basis and its reaction to a discrete image is investigated, then in vector formats an image is synthesized from the system of equations. By analogy, most industrial audio compression formats investigate the response of the approximating basis to the input audio data and, when decoded, reconstruct the audio data from the response from the principle of reversibility of the approximating basis with finite impulse response. At the same time, as a fractal approximating basis is recursive with infinite impulse response, it synthesizes the resulting fractal set. This important difference is the coefficients.
- transformation in space - displacement, reflection, etc ... A close analogy is raster and vector image formats: if raster formats assume the presence of one approximating basis and its reaction to a discrete image is investigated, then in vector formats an image is synthesized from the system of equations. By analogy, most industrial audio compression formats investigate the response of the approximating basis to the input audio data and, when decoded, reconstruct the audio data from the response from the principle of reversibility of the approximating basis with finite impulse response. At the same time, as a fractal approximating basis is recursive with infinite impulse response, it synthesizes the resulting fractal set. This important difference is the coefficients.  ,
, 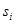 ,
, 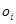 determine the PIFS equations. As a result, it is possible to choose the size of the basis and synthesize more samples of the audio stream per unit time than it was in the original audio stream. A similar result can be observed when scaling vector image formats. This property is implemented in a plugin for Winamp.
determine the PIFS equations. As a result, it is possible to choose the size of the basis and synthesize more samples of the audio stream per unit time than it was in the original audio stream. A similar result can be observed when scaling vector image formats. This property is implemented in a plugin for Winamp.
- Expansion of dynamic range. This is a logical continuation of the property of increasing the frequency of a decoded audio stream - as the bit depth increases from 16 bits to 32 bits, new samples of the audio stream will be synthesized in an extended range.
- Non-deterministic decoding. The PIFS system involves many fractal transformations establishing local similarities. Based on the previously considered expressions, it can be concluded that each of the set of fractal transformations can be performed independently, but the question arises - in what order should they be executed? It is logical to perform in the order in which the fractal analysis was performed, but this conclusion is wrong - each fractal transformation is equivalent to any other of the set. This idea is expressed in the implementation of the choice of the next fractal transformation by a random number generator. For most industrial formats, the reversibility of compression algorithms is the main requirement, but fractal transformations are free from this condition.
Interpretation
Many mathematical concepts have physical interpretations. For example -
 and circle circumference or natural logarithm and spiral shell of the mollusk. Often indicate the relationship of fractal sets with the growth of crystals or trees. However, I would like to present my own interpretation of fractal transformations.
and circle circumference or natural logarithm and spiral shell of the mollusk. Often indicate the relationship of fractal sets with the growth of crystals or trees. However, I would like to present my own interpretation of fractal transformations.I propose to consider the basic expression of the PIFS fractal transform:
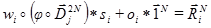
This expression can be represented as the following scheme:

Taking into account the fact that the specified expression describes operations with vectors, consider the scheme of operations on each element of the vector:

I believe that many readers will see the similarity of this scheme with the scheme of an artificial neuron:

conversions
 and
and 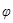 can be considered as a function of addition at the input,
can be considered as a function of addition at the input, 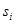 - sensitivity of an artificial neuron at the entrance,
- sensitivity of an artificial neuron at the entrance, 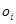 - the level of displacement - the excitation of an artificial neuron. An attentive reader may indicate that the sensitivity of an artificial neuron is determined for each input, while
- the level of displacement - the excitation of an artificial neuron. An attentive reader may indicate that the sensitivity of an artificial neuron is determined for each input, while 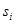 defined as a scalar for all inputs. Also, the reader will indicate the need for the output of the function to determine the state of an artificial neuron in terms of Binary (Boolean) logic: active or inactive. But are such requirements important? Is it acceptable that the sensitivity of an artificial neuron would be the same for all inputs? Yes, there are algorithms for learning artificial neural networks with a similar rule. Is a non-binary value valid at the output of an artificial neuron? At the beginning of the development of the theory of artificial neural networks, when the circuits were built on transistors, capacitors and resistors, they were required to solve simple problems from the field of recognition - for example, recognizing postal codes on postal envelopes and postcards using a perceptron. But with the development of fuzzy logic and the discovery of the advantages of “fuzzy decisions” (soft decisions) over “clear decisions” (hard decisions), the need for such a function can be questioned.
defined as a scalar for all inputs. Also, the reader will indicate the need for the output of the function to determine the state of an artificial neuron in terms of Binary (Boolean) logic: active or inactive. But are such requirements important? Is it acceptable that the sensitivity of an artificial neuron would be the same for all inputs? Yes, there are algorithms for learning artificial neural networks with a similar rule. Is a non-binary value valid at the output of an artificial neuron? At the beginning of the development of the theory of artificial neural networks, when the circuits were built on transistors, capacitors and resistors, they were required to solve simple problems from the field of recognition - for example, recognizing postal codes on postal envelopes and postcards using a perceptron. But with the development of fuzzy logic and the discovery of the advantages of “fuzzy decisions” (soft decisions) over “clear decisions” (hard decisions), the need for such a function can be questioned.What happens if you look at fractal transformations from the point of view of the theory of artificial neural networks? Every element of the vector
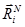 can be considered as one artificial neuron. In this case, the vector
can be considered as one artificial neuron. In this case, the vector 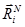 can be considered as a layer of artificial neurons with common properties. However, such “layers” can be several thousand for a small image. Plane transformation
can be considered as a layer of artificial neurons with common properties. However, such “layers” can be several thousand for a small image. Plane transformation  can be interpreted as a trace of connections between artificial neurons. An artificial neural network with linking-topology tracing between layers of artificial neurons for each individual task sounds very unusual, doesn't it? What features can such artificial neural networks have?
can be interpreted as a trace of connections between artificial neurons. An artificial neural network with linking-topology tracing between layers of artificial neurons for each individual task sounds very unusual, doesn't it? What features can such artificial neural networks have?- Recursiveness - the result of the work of an artificial neural network becomes the input data for it itself before establishing an equilibrium state - called for fractal transformations an “attractor”.
- The spiral topology is a condition of local self-similarity.
- Random selection of the sequence of conversions - layers.
- Pre-listening - the ability to set the initial level of an artificial neural network from a real source: image or sound of low quality.
- Acceleration is a simple scaling of an existing artificial neural network by adding or removing artificial neurons from each layer without the need to recalculate the configuration of an artificial neural network. This allows you to create a more detailed state of the network with the generation of new parts.
How can we call such an artificial neural network - a recursive, scalable, asynchronous, non-deterministic artificial neural network with a topology trace and a “soft” solution. An interesting fact is that there already exists an artificial neural network with similar properties - the Hopfield artificial neural network . This artificial Hopfield neural network is also recursive, also converges to a steady state and can be asynchronous. However, it includes one layer, does not include topology tracing, and does not form a “soft” solution. It is interesting that fractal transformations, like the Hopfield artificial neural network, have common filtering properties — recovery of damaged images (of course, fractal transformations can work with real images):



You can see that after removing several elements, fractal transformations can build an image close to the original after one iteration. However, the image “Rose”, which is very different from the original one, creates a very chaotic distribution of pixel intensity. This is consistent with the property of filtering - restoration of damaged images.
Conclusion
At this point you can finish this article. I hope the ideas expressed will turn your attention to the exotic area of fractal transformations.
Source: https://habr.com/ru/post/309906/
All Articles