Analytical calculation of the derivative of a function in the Scala language

Introduction

This algorithm is implemented in the Scala language, a characteristic feature of which is the use of case classes that are so well suited for writing a differentiation algorithm. In this article, it is planned to describe only a part of the program containing the algorithm for finding the derivative, since the development of a parser for mathematical expressions is another big topic,
worthy of a separate article

Training

First, we describe the data structure in which the original mathematical function will be stored. We describe the MathAST treit :

sealed trait MathAST

And his heirs:

 sealed trait SingleToken extends MathAST{ val a: MathAST } sealed trait DoubleToken extends MathAST{ val a: MathAST val b: MathAST } sealed trait LeafToken extends MathAST

SingleToken will implement the case classes of unary operators such as sin (a), -a, ln (a), etc.
DoubleToken describes binary operators: a + b, a ^ b, etc.
LeafToken - “leaves” of a tree, i.e. constants, variables and reserved constant names (pi number and exponent).

We describe the classes / objects of operators and tokens:
')

 case object Pi extends LeafToken case object Exponenta extends LeafToken case class Sin(override val a: MathAST) extends SingleToken case class Cos(override val a: MathAST) extends SingleToken … case class Mul(override val a: MathAST, override val b: MathAST) extends DoubleToken case class Add(override val a: MathAST, override val b: MathAST) extends DoubleToken … case class Differentiate(f: MathAST, dx: Variable) extends MathAST case class Variable(name: String) extends LeafToken case class Constant(value: BigDecimal) extends LeafToken

Pay attention to the Differentiate class, it has a special signature: f is the original function, dx is the variable by which differentiation occurs.

Now there is everything to represent a mathematical function in the form of a tree of calculations, for example, let's take a function: 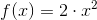$f (x) = 2 \ cdot x ^ {2}$ which will take the form:

Mul (Constant (BigDecimal (2)), Pow (x, Constant (BigDecimal (2)))

Of course, to get a tree expression from a regular string entered by a user, you need to write a parser, but, as mentioned above, this is another topic. Let me just say that the program uses a self-made parser that inherits the Parsers trait from the scala.util.parsing.combinator package.

Algorithm for Finding the Derivative

The basis of which are the rules of differentiation and the table of derivatives .

We describe a recursive function, which will transform the original mathematical function into the resulting derivative function:

 def differentiate(f: MathAST)(implicit dx: String): MathAST

The dx argument containing the name of the variable (by which differentiation occurs) is marked as implicit ( implicit ), this will allow not to transfer it to recursive calls, let the compiler do it.

The input to the recursive function is an expression - the original function f (x) (in MathAST format), the return value is a derivative function 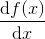$\ frac {\ mathrm {d} f (x)} {\ mathrm {d} x}$ in the same format.

Note 1 : An expression can be a binary, unary or token.
Note 2 : The operator can be one of: "+", "-", "^", "*", "/", "abs", "sin", "cos", "tg", "ctg", " ln "," arcsin "," arccos "," arctg "," arcctg "," (",") ".
Note 3 : Input and output data are presented in MathAST format - tree-expression.

General algorithm

In general, the algorithm is too abstract, so we will analyze it further in more detail.

The recursive function receives data as input and using pattern matching ( pattern-matching ) performs the necessary actions, depending on the data type.
The function calculates the derivative for the input expression and returns the result expression. It may happen that the arguments a and / or b turned out to be not a constant or variable, but a complex function u (x) ,
then you need to recursively calculate the derivative u '(x) , i.e. return [differentiate (u (x))] - go to step 1 with new data - u (x) .
If the data is not correct, return an error message.

Details of the principle of operation and connection with mathematical abstractions

The function took the input data - expression-function, which should be processed in accordance with the rules of differentiation

If binary expression

Binary expressions are marked with a DoubleToken trait . The operator is checked for compliance with one of the available operators ("+", "-", "*", "/", "^"):

 case Add(a, b) => Add(differentiate(a), differentiate(b)) case Sub(a, b) => Sub(differentiate(a), differentiate(b)) …

If “+” operator: return [differentiate (a) + differentiate (b)] .
If the “-” operator: return [differentiate (a) - differentiate (b)] .
If the operator "*": Multiplication is a more complicated case, the operands a and b can be constants or variables (4 combinations in total: u (x) * c , u (x) * v (x) , c * c , c * u (x) ).
The function analyzes which of the 4 options has fallen and returns the expression using the differentiation rule No. 1, No. 3, and No. 5,
if one of the operands is a complex function. For example: if a = u (x) and b = v (x) , then return [differentiate (a) * b + a * differentiate (b))] .
The private isDependsOnVar method checks whether the subexpression depends on the variable by which differentiation is made.
If the operator "/": Actions are similar, as with the operator "*".
If the exponentiation operator “^”: There are also 4 variants of expressions: u (x) ^ c , u (x) ^ v (x) , c ^ c , c ^ u (x) .
The third case is the most non-trivial: u (x) ^ v (x) , to find the derivative of such an expression, you need to use the logarithm and its properties (the description of the logarithm procedure is beyond the scope of this article, therefore we will immediately give the finished formula - № 6).

In the other three cases, standard table formulas are used.

As an example, we give the processing of the multiplication operation:

 case Mul(a, b) => { val u = isDependsOnVar(a) val v = isDependsOnVar(b) if (u && !v) { Mul(differentiate(a), b) } else if (!u && v){ // c^u(x), c=const Mul(a, differentiate(b)) }else if (!u && !v){ // c^c, c=const Constant(BigDecimal(0)) }else Add(Mul(differentiate(a), b), Mul(a, differentiate(b))) }

If unary expression

SingleToken classes are handled as follows:

 case e: SingleToken => val d = e match { case Sin(x) => Cos(x) case Cos(x) => Usub(Sin(x)) case Tg(x) => Div(Constant(BigDecimal(1)), Pow(Cos(x), Constant(BigDecimal(2)))) … } if (isLeaf(ea)) d else Mul(d, differentiate(ea))

The operator is checked for compliance with one of the available operators ("sin", "-", "cos", ...)
For example, the “sin” operator: return [cos (a)] , if a = x , but if a is a complex function u (x) , then return [cos (a) * differentiate (a)] .

With the other operators, similar actions occur, using the rule of differentiation of a complex function and the table rules for taking a derivative.

Separately, you should consider abs - module, since it is not in the table.

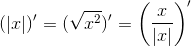
$(| x |) '= (\ sqrt {x ^ {2}})' = \ left (\ dfrac {x} {| x |} \ right) '$

The private isLeaf method finds out whether the function is complex or not; in the first case, you must return the current result multiplied by the derivative of the nested function, and in the second case you simply return the current result.

If one token

It's about a variable or a constant.

 case Variable(a) => if (a == dx) Constant(BigDecimal(1)) else Constant(BigDecimal(0)) case Constant(a) => Constant(BigDecimal(0)) case Pi | Exponenta => Constant(BigDecimal(0)) case _ => throw new AbstractEvaluateException("Differentiate: Wrong input data")

Incorrect data entered, display an error message and exit.
If the variable (by which differentiation is performed, for example, x ), return [1] .
If constant, return [0] .

Finally, add the line:

 case Differentiate(_f, _dx) => differentiate(_f)(_dx.name)

This is in case there is an embedded derivative inside the function, i.e. now higher derivatives can be considered.

I will give the whole code of differentiation, for a better understanding:

 object Derivative { def apply(e: MathAST)(implicit dx: String): MathAST = differentiate(e) def differentiate(f: MathAST)(implicit dx: String): MathAST = f match { case Differentiate(_f, _dx) => differentiate(_f)(_dx.name) case Add(a, b) => Add(differentiate(a), differentiate(b)) case Sub(a, b) => Sub(differentiate(a), differentiate(b)) case Div(a, b) => Div(Sub(Mul(differentiate(a), b), Mul(a, differentiate(b))), Pow(b, Constant(BigDecimal(2)))) case Pow(a, b) => { val u = isDependsOnVar(a) val v = isDependsOnVar(b) if (u && !v) Mul(Mul(Pow(a, Sub(b, Constant(BigDecimal(1)))), differentiate(a)), b) // u(x)^c, c=const else if (!u && v){ // c^u(x), c=const Mul(Mul(Pow(a, b), differentiate(b)), Ln(a)) }else if(!u && !v){ Constant(BigDecimal(0)) }else Mul(Pow(a, Sub(b, Constant(BigDecimal(1)))), Add(Mul(b, differentiate(a)), Mul(Mul(a, Ln(a)), differentiate(b)))) } case Mul(a, b) => { val u = isDependsOnVar(a) val v = isDependsOnVar(b) if (u && !v) { Mul(differentiate(a), b) } else if (!u && v){ // c^u(x), c=const Mul(a, differentiate(b)) }else if (!u && !v){// c^c, c=const Constant(BigDecimal(0)) }else Add(Mul(differentiate(a), b), Mul(a, differentiate(b))) } case e: SingleToken => val d = e match { case Sin(x) => Cos(x) case Cos(x) => Usub(Sin(x)) case Tg(x) => Div(Constant(BigDecimal(1)), Pow(Cos(x), Constant(BigDecimal(2)))) case Ctg(x) => Usub(Div(Constant(BigDecimal(1)), Pow(Sin(x), Constant(BigDecimal(2))))) case Abs(x) => Div(x, Abs(x)) case Ln(x) => Div(Constant(BigDecimal(1)), x) case Sqrt(x) => Div(Constant(BigDecimal(1)), Mul(Constant(BigDecimal(2)), Sqrt(x))) case Usub(x) => Usub(differentiate(x)) case Arcsin(x) => Div(Constant(BigDecimal(1)), Sqrt(Sub(Constant(BigDecimal(1)), Pow(x, Constant(BigDecimal(2)))))) case Arccos(x) => Usub(Div(Constant(BigDecimal(1)), Sqrt(Sub(Constant(BigDecimal(1)), Pow(x, Constant(BigDecimal(2))))))) case Arctg(x) => Div(Constant(BigDecimal(1)), Sub(Constant(BigDecimal(1)), Pow(x, Constant(BigDecimal(2))))) case Arcctg(x) => Usub(Div(Constant(BigDecimal(1)), Sub(Constant(BigDecimal(1)), Pow(x, Constant(BigDecimal(2)))))) case _ => throw new AbstractEvaluateException("Differentiate: Unknown unary operator") } if (isLeaf(ea)) d else Mul(d, differentiate(ea)) case Variable(a) => if (a == dx) Constant(BigDecimal(1)) else Constant(BigDecimal(0)) case Constant(a) => Constant(BigDecimal(0)) case Pi | Exponenta => Constant(BigDecimal(0)) case _ => throw new AbstractEvaluateException("Differentiate: Wrong input data") } private def isLeaf(e: MathAST): Boolean = e match { case Variable(_) | Constant(_) => true case Pi | Exponenta => true case _ => false } private def isDependsOnVar(tree: MathAST)(implicit dx: String): Boolean = tree match{ case e: DoubleToken => (ea match { case Variable(name) => if(name == dx) true else false case _ => isDependsOnVar(ea) })||(eb match { case Variable(name) => if(name == dx) true else false case _ => isDependsOnVar(eb) }) case e: SingleToken => isDependsOnVar(ea) case Variable(name) => if(name == dx) true else false case _ => false } }

Conclusion

All source code can be downloaded on github , you can test the program online on the Derivatives Calculator site online , the application is implemented as a REST service and supplemented with expression simplification modules.

Bibliography

Mathematical portal «mathprofi.ru» mathprofi.ru/slozhnye_proizvodnye_logarifmicheskaja_proizvodnaja.html
Odersky M. “Programming in Scala (second edition)”
Hostmann K. "Scala for the impatient"

Source: https://habr.com/ru/post/309676/

All Articles