Geekly Articles each Day
📜 ⬆️ ⬇️

The logic of consciousness. Part 5. The semantic approach to the analysis of information


The well-known Turing test says that it is possible to understand whether a car thinks or not, whether we can distinguish it from a person in a conversation or not. At the same time, it is meant that not a small talk will be conducted, but, in fact, an interrogation with an addiction in which we will try in every way to drive the car to a dead end. What are we going to check? Only one thing - does the car understand the essence of the questions we ask. Whether she tries, simply, to formally manipulate words or she can correctly interpret the meanings of words, using the knowledge gained earlier in the conversation, or, in general, the knowledge generally known to people.

Perhaps, during the test it is not particularly interesting to ask the car: when was the Battle of Kulikovo. Much more interesting is what she will say, for example, about: why do we push harder on the buttons of the console, which have batteries?

The difference in human thinking and most computer algorithms is related to the question of understanding meaning. As a rule, rather strict rules are laid down in a computer program that determine how the program perceives and interprets input information. On the one hand, this limits the freedom of communication with the program, but, on the other hand, it allows you to avoid errors associated with the incorrect interpretation of unclear formulated statements.

Globally, the problem of transmitting meaning, no matter from person to person or from person to computer, or between computers, looks like this: the clearer and more unambiguous we want to convey a message, the higher requirements are imposed on the consistency of the terms used on the sending and receiving side.
')
If we want the program to run equally on any computer, we create conditions for the unambiguous interpretation of all commands. When we write mathematical formulas, their interpretation does not depend on the will of the interlocutor. Pursuing science, to achieve mutual understanding, we use, where possible, not words of everyday language, but clearly defined scientific terms.

Sometimes, it seems that a clear mathematical-algorithmic approach is a higher level of information presentation compared to the fuzzy semantics of a natural language. But at the same time, we often encounter the fact that it is much easier for us to understand a complex thought not when it is written down in detail and mathematically strictly, but when we are briefly and figuratively explained in natural language to its essence.

Next, I will show what lies behind the fuzzy semantic descriptions and in which direction it might be worth moving the computer to pass the Turing test.

Cryptography and meaning


Consider an example from the field of cryptography. Suppose we have a stream of encrypted messages. The encryption algorithm is based on replacing the symbols of the original message with other symbols of the same alphabet according to the rules that are determined by the encryption mechanism and key. Alan Turing dealt with something similar, cracking the code of the German Enigma .



Suppose that the rules for replacing letters are completely determined by the keys. Suppose that there is a finite set of keys and for each key, replacement rules are specified, such that each letter has a one-to-one correspondence. Then, in order to decrypt any message, it is necessary to go through all the keys, apply reverse transcoding and try to figure out if there is any meaningful one among the decryption options.

To define meaningfulness, a dictionary with words that may appear in the decoded message is required. As soon as the message takes the form in which the words of the message coincide with the words from the dictionary, we can say that we have found the correct key and received the decrypted message.

If we want to speed up the selection of the key, then we will have to parallelize the verification process. Ideally, you can take as many parallel processors as there can be different keys. Distribute the keys among the processors and decode each processor with its own key. Then on each processor to make a check of the result obtained for meaningfulness. In one pass, we will be able to test all possible hypotheses about the code used and find out which one is most suitable for decrypting the message.

To check the meaningfulness of each of the processors must have access to the dictionary of possible words in the message. Another option is that each of the processors must have its own copy of the dictionary and refer to it for verification.

Now we make the task more interesting. Suppose that at the beginning we know only a few words that make up our initial vocabulary. At the same time, we know all the keys and recoding rules. Then in the message flow we will be able to pick up the key only for those messages that contain at least one of the known words.

When we find out the correct code for a few decrypted messages, we will get the correct spelling for other previously unknown words. These words can be added to the dictionary of the processor that found the correct answer. In addition, new words can be transferred to all other processors and replenish their local dictionaries. As we gain experience, we will decipher an increasing percentage of messages until we get a complete dictionary and a decryption performance close to one hundred percent.

There are situations when several keys will immediately display words in the recoded message in the recoded message. In this case, you can either ignore such messages, considering them to be undeciphered, or choose the key that gives a greater number of matches of words from our dictionary. Random occurrences of meaningful words are also possible, then it will be necessary to introduce the sign “presumably” for new words and change it to sign “confirmed” when such a word is encountered repeatedly in deciphered texts.
The resulting simple cryptographic system is interesting in that it allows you to introduce the concept of "meaning", which is essentially close to what we usually call meaning, and give an algorithm that allows you to work with it.

The result of decoding obtained with a certain key can be called an interpretation or interpretation of the original coded text in the context of this key. The algorithm for determining the cryptographic meaning is a check of all possible code interpretations and a choice of one that looks most plausible from the point of view of memory, which stores all previous experience of interpretations.

The meaning of information


The interpretation of the meaning and the algorithm for its definition, introduced for a cryptographic problem, can be expanded for the more general case of arbitrary informational messages composed of discrete elements.

We introduce the term "concept" - c (concept). Let us assume that all of us have access to N concepts. A set of all available concepts forms a dictionary.


We will call the information message of length k a set of concepts where i j ∈C

We will assume that a message can be matched with its interpretation I int (interpretation). The treatment of a message is also an informational message consisting of the concepts of the set C.

We introduce the rule of obtaining interpretations. We will assume that any interpretation is obtained by replacing each concept of the original message with some other concept or with itself. In this case, the first concept of the message goes into the first concept of interpretation, and so on.
Suppose that in what kind of replacements are carried out in the interpretation, there is a certain system, which is generally unknown to us.

We introduce the concept of “subject” S. For a subject, we define his memory, that is, personal experience as a set of information known to him, which has been interpreted. Information coupled with the interpretation can be recorded as a pair


Then the memory can be written as the set of all such pairs.


Assume that there is a teacher who is ready for each message to provide its correct interpretation. We will conduct the primary education phase using the capabilities of the teacher. We will memorize messages and interpretations given by the teacher, as pairs of the form “message - interpretation”.

Based on the memory formed with the teacher, we can try to find a system in the comparison of concepts and their interpretations. The simplest thing we can do is to collect for each concept all its possible interpretations that are stored in memory and to obtain a range of possible meanings of the concept. According to the frequency of use of one or another interpretation, it is possible to give an estimate of the probability of the corresponding interpretation.

But in order to really find a system in comparison, we need to solve the clustering problem by some rational method and divide mi objects into classes according to the same criteria as the interpretation of the same concepts within the class. We will try to make sure that for all objects within one class the same rules of interpretation of the concepts included in them act. That is, if for a single memory, referred to a specific class, a certain concept passes into a certain interpretation, then it will also move to the same interpretation in all other memories of this class.

Pay attention to the peculiarities of the carried out clustering. The distance between memories is calculated not by the similarity of the original descriptions or interpretations obtained, but by how similar the rules were used when obtaining interpretations from the original description. That is, it is not the memories that look like each other that are combined into classes, but the memories for which turned out to be the general rules of interpretation, the concepts included in them.

We will call the classes obtained as a result of such clustering “contexts” - Context .

The totality of all contexts for subject S forms the context space.
{Context i | i = 1 ... N Context }.

For each i context, you can specify a set of rules for interpreting concepts.


The set of rules for the context is a set of pairs of “initial notion - interpretation”, describing all transformations peculiar to the context.

After completion of the primary training stage, you can enter an algorithm that allows you to interpret new information. We select from memory M memory M int , consisting solely of interpretations


We introduce a measure of the consistency of interpretation and memory of interpretations. In the simplest case, this may be the number of coincidences of the treatment and the memory elements, that is, how many times such an interpretation occurs in the memory of interpretations.


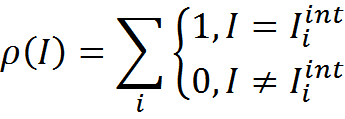
Now, for any new information I, for each context Context j we can get the interpretation I j int , applying the transformation rules R j to the initial information. Further, for each resulting interpretation, it is possible to determine its consistency with the interpretation memory.


The calculation scheme for one context is shown in the figure below.

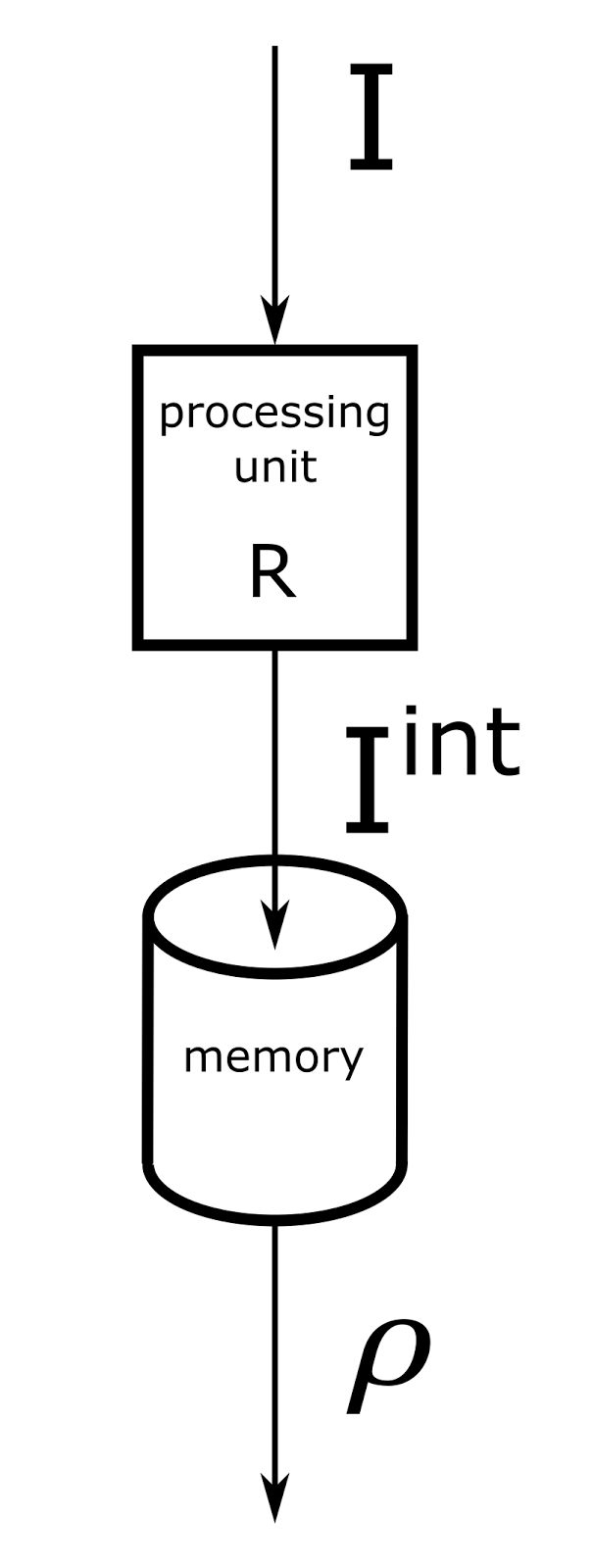
Computing scheme of a single context module

We introduce the probability of interpretation of information in the context of j


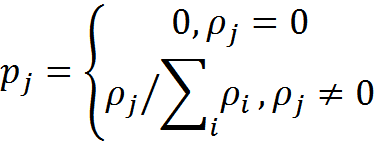
As a result, we obtain the interpretation of information I in each of K possible contexts and the probability of this interpretation.


If all probabilities are zero, then we state that the information by the subject is not understood and does not make sense to him. If there are probabilities other than zero, then the corresponding interpretations form a set of possible meanings of information.

If we decide to decide on one main interpretation of the information for a given subject, then we can use the context with the maximum probability value.

As a rule, information contains not one, but several meanings. Additional meanings can be distinguished if we take interpretations different from the main context with a non-zero probability. But this procedure has its pitfalls. When choosing, it is necessary to take into account the possible correlation of contexts. Later we will look at this in more detail.

As a result, the concept of "meaning" can be described as follows. The meaning of certain information for a specific subject is a set of interpretations that are most successful in terms of the correspondence of these interpretations and the memory of the subject, obtained as a result of analyzing information in various contexts, built, in turn, on the experience of this subject.

The general scheme of calculations related to the definition of meaning can be depicted as a set of parallel contextual computational modules (figure below). Each of the modules interprets the original description according to its system of transformation rules. The memory of all modules is the same in content. Comparison with memory gives an assessment of the conformity of interpretation and experience. Based on the probabilities of interpretations, a specific meaning is selected. The procedure is repeated until the basic semantic interpretation of information is exhausted.


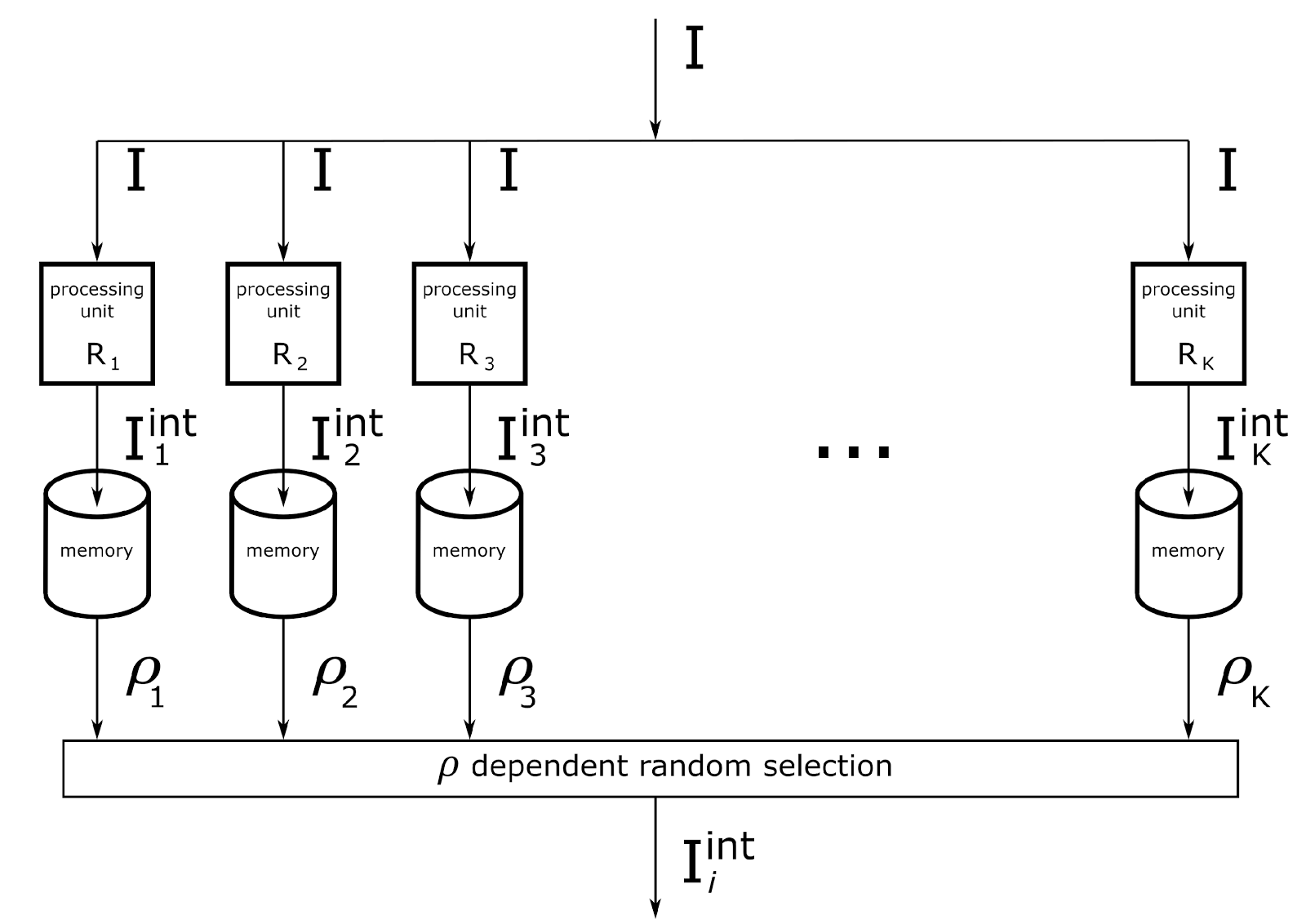
Computational scheme for determining one of the meanings in a system with K contexts

Once the meaning of the information has been determined, you can add new memories to the memory. This new experience can be used to define the interpretation of subsequent information and to clarify the context space and transformation rules. Thus, it is possible not to single out a separate stage of primary education, but simply to accumulate experience, while improving the ability to isolate meaning.

The described approach linking information and its meaning contains several key points:


Brute force problem


The described algorithm for determining meaning is very closely related to the question of the equality of the classes P and NP , which is also known as the search problem. A foul search problem can be described as follows: if there is a question and there is an answer to this question, and you can quickly verify the correctness of this answer (in polynomial time), can you also quickly find the correct answer to this question (in polynomial time and using polynomial memory ).

For example, suppose we have a table of primes, a certain number, and the statement that a certain set of primes is an expansion of that number. To check this statement, it is enough to multiply the primes from the proposed set and see if our result will be as a result. But if we just want to find the expansion of this number into prime factors, then we will encounter the need to look through all the simple factors. With an increase in the digit capacity of the original number, the number of primes that need to be searched grows exponentially. Accordingly, a brute-force solution turns out to be exponentially complex with respect to the linear increase in the complexity of the condition. The question of the equality of the classes P and NP is the question of whether there are algorithms for this and other complex, brute-based problems that can solve them in polynomial time and memory complexity of the input data. If any “complex” task can be reduced to “simple”, then the classes are equal.

At present, the question of equality of classes is open, but most mathematicians are inclined to think that these classes are not equal. Since the operation of all public-key encryption algorithms is based on the fact that there is something that is easy to verify, but difficult to find, this means that, according to most mathematicians, cryptography can be reliable.

In our case, we have a set of concepts, descriptions composed of these concepts and some learning experience, when we are given the correct interpretations for some descriptions.
Based on the training data, we can compile the spectra of possible interpretations. That is, for each concept, see what interpretations it took and assume that there are no other interpretations for it.

Now you can try to give an interpretation of any description. Suppose that we have a vast experience and the memory we use has all the possible correct interpretations for any descriptions. Then it is possible to make all possible joint combinations from the spectra of interpretations admissible for the concepts included in the description and see if any of them looks like the contents of the memory. Since our memory is huge, then there surely will be a coincidence (if, of course, the original phrase is correct). If it is the only one, then this will be the correct interpretation of the original description.

The number of combinations that need to be sorted out will be equal to the product of the sizes of the spectra of all concepts of the original description. For example, to describe from 10 concepts with 10 possible interpretations for each concept, we get 10 billion variants. With an increase in the length of the description and the number of interpretations, with an exponential growth, we obtain the so-called combinatorial explosion.

You can draw a rough analogy with the translation from one language to another. Having samples of texts and their translations, it is possible for each word to make a range of its possible translations into another language. The conditionally correct translation variant (we will not take into account anything other than the translation of the words themselves) will be one of the combinations made up of the spectra of possible translations of individual words. For a real language, in most cases we will get hundreds of millions, trillions or more combinations. This will require a base of all valid sentences. You can imagine its size.

The contextual approach allows us to significantly simplify calculations by highlighting patterns in the system of interpretations. If there are some general rules for comparing concepts and their interpretations, then observing the correct examples of interpretation allows us to single out these rules. The scope of the general rules we called contexts. To test hypotheses about the possible interpretation of input information, it is now sufficient to check only those interpretations that occur in contexts.

The number of necessary contexts is determined by the nature of the input information and the accuracy of understanding the meaning we want to receive. For practical purposes, no more than a million contexts are almost always enough for good results, despite the fact that the total number of combinations can be higher by many orders of magnitude.

If we continue the example with the translation, the contextual approach suggests that you can select a fixed number of semantic contexts within which the translation for many words will be coordinated with each other. For example, if it is possible to determine that the text is of a scientific nature, then from the spectrum of possible interpretations of many words almost all the options will go except one. Similarly with other topics.

It is possible to determine which context should be preferred in the translation, based on the context in which the interpretation of the phrase looks more likely. Including on the basis of how often phrases with such a set of words are found in this context. In what is described, one can see a lot in common with the methods used in real translation systems, which is not surprising.

Frames


The described contextual model, in many respects, solves the same tasks as the concept of frames of Marvin Minsky (“A Framework for Representing Knowledge”, Marvin Minsky). Common tasks that confront models inevitably lead to similar implementations. Describing frames, Minsky uses the term "microcosms", meaning by it situations in which there is a certain consistency of descriptions, rules and actions. Such microworlds can be matched with contexts in our definition.The selection of the most successful frame from memory and its adaptation to the real situation can also be largely compared with the procedure for determining the meaning.

When using frames to describe visual scenes, frames are interpreted as different “points of view”. At the same time, different frames have common terminals, which makes it possible to coordinate information between frames. This corresponds to how, in different contexts, the rules of interpretation can lead different initial descriptions to the same descriptions-interpretations.

An object-oriented approach popular in programming, directly related to frame theories, uses the idea of ​​polymorphism, where the same interface, when applied to objects of different types, causes different actions. This is close enough to the idea of ​​interpreting information in the appropriate context.

For all the similarity of the approaches associated with the need to answer the same questions, the context-semantic mechanism differs significantly from the frame theory and, as will be seen later, cannot be reduced to it.

The peculiarity of the context-semantic approach is that it is equally well applicable to all types of information that the brain encounters and operates with. The various zones of the cortex of the real brain are extremely similar in terms of internal organization. It makes you think that they all use the same principle of information processing. It is very likely that the approach of highlighting meaning can claim the role of such a unified principle. Let's try on several examples to show the basic ideas of applying the semantic mechanism.

Semantic information


The words that make up the phrases can be interpreted differently depending on the general context of the narration. However, for each word, you can make a range of meanings, described in other words. If we follow up on what the different interpretations of the same words depend on, we can distinguish the thematic areas of interpretation. Within such areas, many words will have an unambiguous meaning defined by the subject area. A collection of such subject areas is a context space. Contexts can be related to narrative time, number, gender, subject area, subject matter, and so on.

A similar situation associated with the choice of a possible interpretation for each of the words of a phrase occurs when translating from one language to another. Possible options for the translation of a word clearly show the range of possible meanings of the word (figure below).

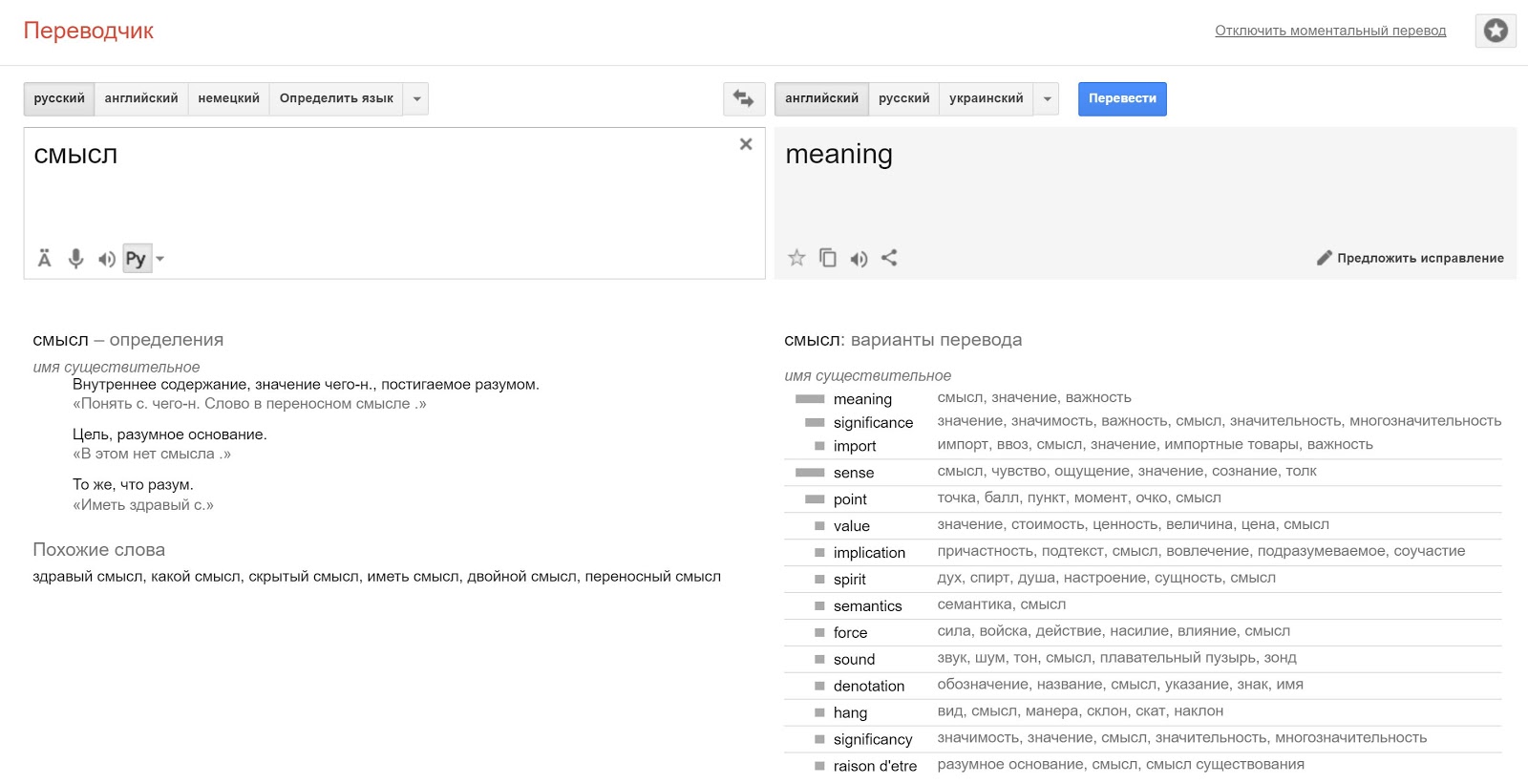
An example of a spectrum of possible interpretations arising in translation.

Definition of the meaning of a phrase is the choice of such a context and obtaining such interpretations of words that create the most plausible sentence, based on the experience of someone who tries to understand this meaning.

There may be situations where the same phrase in different contexts will create different interpretations, but at the same time these interpretations will be permissible, based on previous experience. If the task is to determine the only meaning of such a phrase, then it is possible to choose the interpretation that has a higher match with the memory and, accordingly, the probability calculated for it. If the phrase was originally composed as ambiguous, then it is appropriate to perceive each of the meanings separately and state the fact that the author of the phrase, voluntarily or unwittingly, managed to combine them in one statement.

Natural language is a powerful tool for expressing and conveying meaning. However, this power is achieved due to the fuzziness of interpretations and their probabilistic nature, depending on the experience of the perceiving subject. In most domestic situations, this is sufficient for a brief and fairly accurate transfer of meaning.

When the transmitted meaning is rather complicated, as it happens quite often, for example, when discussing scientific or legal issues, it makes sense to switch to the use of special terms. The transition to terminology is the choice of the interlocutors of an agreed context in which the terms are interpreted by the interlocutors in the same and unambiguous way. For such a context to be available to both interlocutors, each of them needs relevant experience. For the same understanding of the experience should be similar, which is achieved through appropriate training.

For a natural language, you can use a measure of consistency of context and memory, based not only on the complete coincidence of descriptions, but also on the similarity of descriptions. Then more possible meanings become available and the possibility of additional interpretation of phrases appears. For example, in this way one can correctly interpret phrases containing errors or internal contradictions. Or spoken figuratively, or figuratively.

In determining the meaning is easy to take into account the general context of the narrative. So, if a phrase is interpretable in different contexts, preference should be given to contexts that were active in previous phrases and set the general context. If the phrase permits interpretation only in a context different from the main narration, then this should be perceived as switching the narration to another topic.

Audio information


An analogue audio signal is easily converted to a discrete form. To do this, the time sampling is first performed when the continuous signal is replaced by measurements taken at the sampling frequency. Then the amplitude quantization is done. In this case, the signal level is replaced with the number of the nearest quantization level.

The resulting recording of the signal can be divided into time intervals and perform for each of them the window Fourier transform. The result will be a recording of the sound signal as a sequence of spectral measurements (figure below).


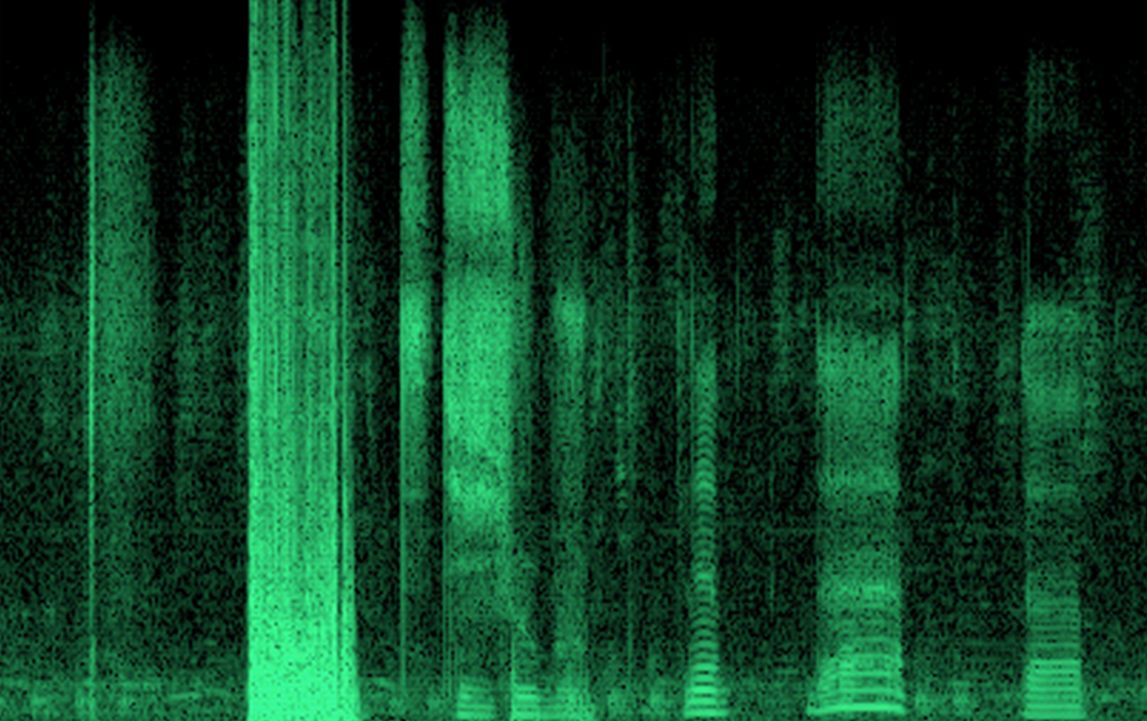
EXAMPLE timebase spectrum of the speech signal

introduce a ring identifier with a period for N time slots T . That is, first we number N T ranges from 1 to N T . N T + 1 interval numbering again 1 and so on. As a result, we get the same numbers every N T intervals.

Suppose that the Fourier transform contained N F frequency intervals. This means that each spectral measurement will contain N F complex values. We replace each complex value with its amplitude and phase and perform their quantization. Amplitude with N A quantization levels, phase with N Plevels.

Within the range of N T time intervals, each element of the spectrum record can be described by the combination: time interval code, frequency value, amplitude value, phase value. We carry a set of concepts C , allowing to describe the sound within the interval defined by the period of the ring identifier. These will be all possible combinations.


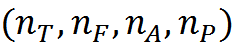
In total such concepts will be.


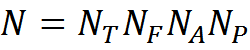
Accordingly, the set of concepts C will contain N elements.


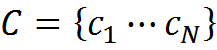
Any sound signal with a duration of no more than N T time intervals can be recorded as information by listing such concepts.
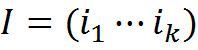where i j ∈C

With the help of the same concepts one can write down any interpretation.

If you look at the picture with the recording of the spectrum of the speech signal, then each of these sound concepts is a point with specific coordinates and brightness. There is a phase, but it is not visible in the picture. Having a set of all points with all possible colors (amplitudes), we, naturally, can draw any picture.

The task of recognizing sound images requires recognition of the same sound image, provided that the current sound can be transformed with respect to what is stored in memory. The main sound transformations are a change in volume, a change in tone of sound, a change in tempo and a shift in the beginning of sound.

These transformations correspond to:


We introduce a context space that covers possible combinations of transformations. For each context, you can create transition rules, that is, describe how each of the initial concepts will look in the context of the corresponding transformation. For example, in the context of changing the frequency one position up, all concepts will receive an interpretation that shifts them one position down. A pure tone at a frequency of 1 kHz is the same as a tone at a frequency of 900 Hz in the context of a general upward shift of sound by 100 Hz. Similarly with other types of transformations.

After describing the transition rules of concepts in different contexts, it will be possible to recognize the same sound images regardless of their transformations. The moment of utterance, volume, voice pitch and speech speed will not affect the ability to compare current information with that stored in memory. The current sound will be converted to different interpretations in all possible contexts. In the context that corresponds to the desired transformation, the description will take the interpretation in which you can easily learn something already heard before.

In practice, when working with complex signals, such as speech, it is impossible to do with one processing step. First, it is advisable to limit the selection of simple phonemes. The contexts will contain the rules for the transformation of elementary sounds, as described above. Then make a description, consisting of phonemes. In this case, the phoneme will be quite a complex element that identifies not only the sound form, but also its height, temporal position and the speed of pronunciation. Information composed of phonemes, in turn, may be subjected to subsequent processing in a new context space.

Contexts can be complicated without being limited to simple transformations. In this case, the very definition of a suitable context creates additional information. For example, for speech, contexts are different intonations and language accents. Intonation and accent contexts allow not only to improve the accuracy of recognition, but also to gain additional knowledge about how the phrase is said.

Visual Information


Consider the most simple ways to work with the image. Suppose that we have a raster image consisting of points for which their color is given. We translate the image in black and white, leaving only the brightness values ​​of the points. Perform image contour selection (for example, using the Canny algorithm ( JOHN CANNY, A Computational Approach to Edge Detection ) (picture below)).


Result of border selection.

Now we divide the image into small square areas. In each small area through which the boundary line passes, this line can be approximated by a straight line segment. Let us set the number of quantization orientation N O and determine the appropriate direction. Now for each square, if it contains a border, you can specify the number of the direction most closely related to the orientation of the border. It is possible to introduce more complex and, accordingly, more accurate descriptions, but for example, such a simplified model will suit us.

Assume that the mesh size, dividing the image into areas, N X to N Y . We introduce a set of concepts C which will include concepts that correspond to all possible combinations


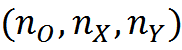
Such concepts will be.


Accordingly, the informational description of the image can be reduced to an enumeration of the corresponding concepts
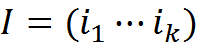, where i j ∈C.

Now we will be interested in the problem of invariant recognition of images. Let's set a set of transformations in relation to which we want to achieve invariance. The most common transformation practices:


These transformations are the most interesting, since they correspond to how the projection of a flat figure changes during its spatial movements and turns.

Now create the context space. To do this, we implement the quantization of the transformation parameters, that is, we divide them into discrete values. And create as many contexts as there are possible combinations of these parameters.

For each context, you can describe the rules for the transformation of concepts. So, the vertical line will become horizontal when rotated 90 degrees, the vertical line at position (0,0) will become the vertical line at position (10.0) with a horizontal shift of 10 positions and so on.

After specifying the transformation rules, it is enough to see once and remember an image, so that upon presentation of it in a transformed form, you can determine both the image and the type of transformation. Each context will translate the description into an interpretation characteristic of this context, that is, perform a geometric transformation of the description, and then compare it with the memory for a match. If such a check is conducted in parallel in all contexts, then in one measure one can find the meaning of the initial information. In this case, it will be the recognition of the image, if we were familiar with it, and the definition of its current transformation.

Can not be limited to the described transformations. You can use, for example, the transformation of the "bending sheet" and the like. But increasing the number of transformations leads to an exponential increase in the number of contexts. In practice, the problem of image processing by the described method allows for very strong optimization, which allows for real-time calculations. Based on such ideas, but more advanced algorithms will be described in detail later.

The main idea of ​​the described approach is that in order to obtain an invariant representation of an object, it is not necessary to conduct long-term training, showing this object from different angles. It is much more effective to teach the system the rules of basic geometric transformations peculiar to this world and uniform for all objects.

A partially described approach is implemented in well-proven convolutional networks (Fukushima, 1980) (Y. LeCun and Y. Bengio, 1995). To obtain shift invariance in convolutional networks, the convolution kernel describing the desired image is applied to all possible positions horizontally and vertically. This procedure is repeated for all familiar network of images in order to determine the most accurate match (figure below). In fact, this algorithm declares a “wired” a priori knowledge of the transformation rules under horizontal and vertical shears. Using this knowledge, he forms the space of possible contexts realized by layers of simple artificial neurons. The definition of the maximal coincidence during convolution for various nuclei is similar to the definition of meaning described by us.


, (Fukushima K., 2013)



The function of the treatment of interpretation and memory is used to determine the likelihood of realization of the context corresponding to this interpretation. By the way our brain chooses meaning in real situations, it can be assumed that matching algorithms can be quite complex and not be reduced to one simple formula.

Earlier, we cited the example of a “hard” match function based on exact match of descriptions. For memory interpretations


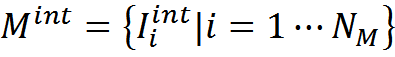
Matching function


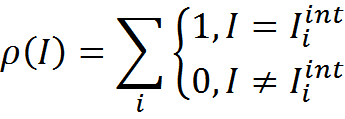
We introduce a measure of the comparison of descriptions Q. A measure based on an exact match can be written


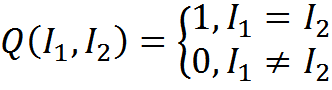
The match function takes the form


Matching, based on exact coincidence, allows to determine the meaning only if at least in one context there is an interpretation that is already stored in memory. But you can imagine a situation where it is appropriate to find the most appropriate context for interpreting the description, even in the absence of exact matches. In this case, you can use a less rigorous comparison of descriptions. For example, you can enter a measure of similarity of descriptions based on the number of concepts common to the two descriptions.

We have already talked about the possibility of encoding descriptions by adding bitmaps into a Bloom filter (Bloom, 1970). Let us compare each concept from the dictionary C with its discharged binary code of length m, containing k units.



Then each description I , consisting of n concepts, can be associated with a binary array B, obtained from the logical addition of the codes of the concepts included in the description.


The similarity of the two descriptions can be judged by the similarity of their binary representations. In our case, the measure of similarity based on their scalar product is appropriate.

The scalar product of two binary arrays shows how many units coincided in these two arrays. There is always a chance that the units in binary descriptions will coincide randomly. Waiting for the number of randomly matched units of M depends on the length of the binary code, the number of units encoding one concept, and the number of concepts in the descriptions. To get rid of the random component, the measure of similarity can be adjusted by the amount of random expectation.


Such a measure may take negative values, which in themselves do not make sense. But with the addition of measures of proximity for all memory elements, they will compensate for random positive outliers. Then the match function can be written


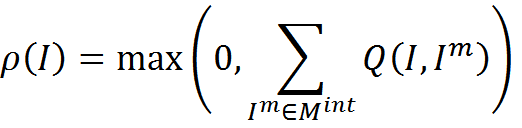
With a “soft” assignment of the correspondence function, our model moves towards a statistical evaluation of the probabilities of a particular context and can be compared with Bayesian methods hidden by Markov models and fuzzy logic methods.

"Hard" and "soft" approaches have both their advantages and their disadvantages. A soft approach allows you to get a result for information that does not have a clear analogue in memory. This may be the case when the description itself contains inaccuracies or errors. In such cases, by defining the preferred context, the most similar correct memory can be used as an interpretation.

In addition, a soft comparison gives the result when the descriptions stored in the memory contain details that are irrelevant for the purpose, which can be considered informational noise. However, a tough approach can produce a fundamentally better result. In most cases, getting into a rare, but adequate description for the description, is much preferable to patterned interpretations based on "external" similarity.

Another, perhaps, the most interesting approach is possible if, in the set of all descriptions, we first isolate the factors responsible for certain entities common to some of the descriptions. Then you can build a matching function, as a soft or hard comparison with the portraits of factors. This approach is good because it allows you to determine the presence of factors unambiguously or with a certain probability against the background of information noisy with other descriptions.

The combined approach using all kinds of conformity assessments seems reasonable. Most importantly, the definition of meaning is not a self-contained operation. Correct definition of meaning is the basis for subsequent information operations related to the thinking and behavior of the subject. As will be shown later, the behavior and thinking algorithms are determined by reinforcement learning mechanisms, which make it possible to form the most mental moves and behavioral acts appropriate to the situation. It can be assumed that, with the definition of meaning, the best result will not be some rigidly defined strategy for calculating the compliance function, but calculation based on reinforcement learning, which will optimize the calculation function based on the success of previous evaluations.

In the next part, I will show how the real brain may work with the meaning and tell you how to use the pattern-wave model, holographic memory and understanding of the role of cortex minicolumns, you can try to justify how the context space, implemented on biological neurons, looks.

Alexey Redozubov

The logic of consciousness. Introduction
The logic of consciousness. Part 1. Waves in the cellular automaton
The logic of consciousness. Part 2. Dendritic waves
The logic of consciousness. Part 3. Holographic memory in a cellular automaton
The logic of consciousness. Part 4. The secret of brain memory
The logic of consciousness. Part 5. The semantic approach to the analysis of information
The logic of consciousness. Part 6. The cerebral cortex as a space for calculating meanings.
The logic of consciousness. Part 7. Self-organization of the context space
The logic of consciousness. Explanation "on the fingers"
The logic of consciousness. Part 8. Spatial maps of the cerebral cortex
The logic of consciousness. Part 9. Artificial neural networks and minicolumns of the real cortex.
The logic of consciousness. Part 10. The task of generalization
The logic of consciousness. Part 11. Natural coding of visual and sound information
The logic of consciousness. Part 12. The search for patterns. Combinatorial space

Source: https://habr.com/ru/post/309626/

More articles:


All Articles