Stockholm City Library. Photo minotauria .

In this article I want to tell you that evaluating the time to access memory as O (1) is a very bad idea, and instead we should use O (√N). First, we consider the practical side of the issue, then the mathematical side, based on theoretical physics, and then we consider the consequences and conclusions.

Introduction

If you studied computer science and analysis of algorithmic complexity, then you know that the passage through the linked list is O (N), the binary search is O (log (N)), and the search for an element in the hash table is O (1). What if I tell you that all this is not true? What if the pass through the linked list is actually O (N√N), and the search in the hash table is O (√N)?

Do not believe? I will convince you now. I will show that memory access is not O (1), but O (√N). This result is valid both in theory and in practice. Let's start with the practice.

Measure

Let's first define the definitions. The “O” notation is great for many things, from memory usage to running instructions. In this article, we O (f (N)) will mean that f (N) is the upper bound (worst case) for the time it takes to gain access to N bytes of memory (or, respectively, N equal-sized elements ). I use Big O to analyze time, but not operations , and this is important. We will see that the CPU is waiting for a long slow memory. Personally, I don’t care what the processor is doing while waiting. I only care about the time, how long this or that task is completed, so I limit myself to the definition above.

Another note: RAM in the header means random access (random memory accesses) as a whole, and not some specific type of memory. I consider the time to access information in memory, be it a cache, DRAM or swap.

Here is a simple program that runs through a coherent list of size N. Dimensions - from 64 elements to 420 million elements. Each list node contains a 64-bit pointer and 64 bits of data. Nodes are mixed in memory, so each memory access is arbitrary. I measure the passage through the list several times, and then mark on the chart the time it took to access the item. We should get a flat graph of the form O (1). Here is what happens in reality:

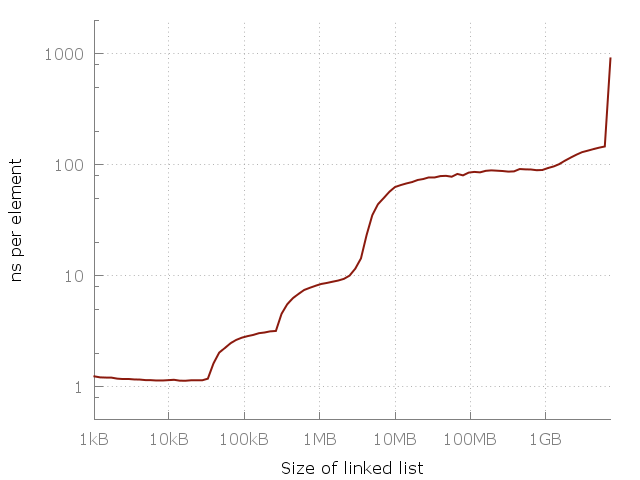
The difficulty of accessing an item in the linked list. Accessing an arbitrary item in a 100-megabyte list is about 100 times slower than accessing an item in a 10-kilobyte list.

Notice that this chart uses a logarithmic scale on both axes, so the difference is really huge. From about one nanosecond per element, we have reached a whole microsecond! But why? The answer, of course, is cache. System memory (RAM) is actually quite slow, and to compensate, smart computer designers add a hierarchy of faster, closer and more expensive caches to speed up operations. My computer has three cache levels: L1, L2, L3, 32 kb, 256 kb and 4 mb in size, respectively. I have 8 gigabytes of RAM, but when I ran this experiment, I had only 6 free gigabytes, so in the latter I started swapping to disk (SSD). Here is the same graph, but with the size of the caches.

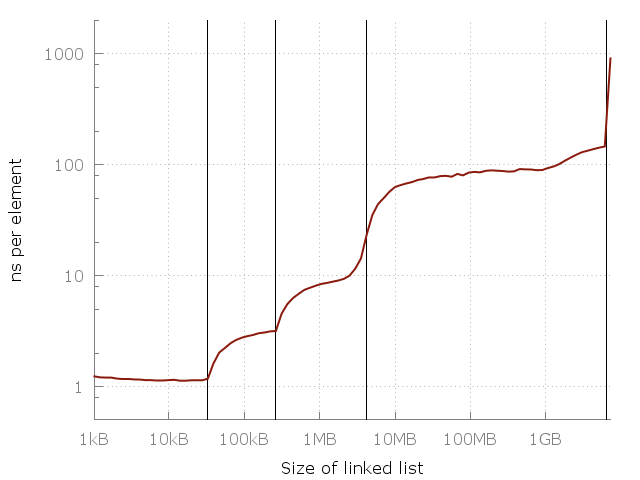
The vertical lines indicate L1 = 32 kb, L2 = 256 kb, L3 = 4 mb and 6 gigabytes of free memory.

This graph shows the importance of caches. Each cache layer is several times faster than the previous one. This is the reality of modern CPU architecture, be it a smartphone, laptop or mainframe. But where is the general pattern? Can a simple equation be placed on this graph? It turns out we can!

Let's take a closer look, and note that between 1 megabyte and 100 megabytes is about a 10-fold slowdown. And the same between 100 megabytes and 10 gigabytes. It seems that every 100-fold increase in used memory gives a 10-fold slowdown. Let's add this to the chart.

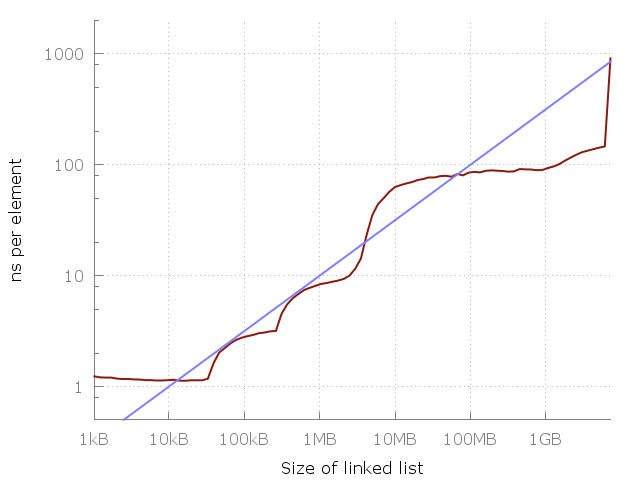
The blue line is O (√N).

The blue line is a graph indicating O (√N) cost of each memory access. Seems great, right? Of course, this is my particular car, and your picture may look different. However, the equation is very easy to remember, so maybe it should be used as a rough rule.

You probably ask, but what's next, right of the schedule? Does the increase continue or does the schedule go flat? Well, it becomes flat for a while, while the SSD has enough free space, after which the program will have to switch to the HDD, then to the disk server, then to the far data center, and so on. Each jump will create a new flat area, but the general trend for improvement, I think, will continue. I did not continue my experiment due to lack of time and lack of access to a large data center.

“But the empirical method cannot be used to define the boundaries of Big-O,” you say. Of course! Perhaps, there is a theoretical border at a delay at memory access?

Round Library

Let me describe a thought experiment. Suppose you are a librarian working in a circular library. Your table is in the center. The time you need to get any book is limited by the distance you need to go. And in the worst case, this is the radius, because you need to reach the very edge of the library.

Suppose your sister works in another similar library, but she has (at the library, not sister :), - approx. lane.) radius twice. Sometimes she needs to go twice as much. But its library has 4 times more space than yours, and it has 4 times more books. The number of books is proportional to the square of the radius: N∝ r². And since the time T of access to the book is proportional to the radius, then N∝ T² or T∝√N or T = O (√N).

This is a rough analogy with the central processor, which needs to get data from its library - RAM. Of course, the speed of the “librarian” is important, but here we are limited by the speed of light. For example, in one cycle of a 3-gigahertz processor, light travels a distance of 10 cm. So, for a trip back and forth, any instantly available memory should be no more than 5 centimeters from the processor.

Well, how much information can we place within a certain distance r from the processor? Above, we talked about a round flat library, but what if it is spherical? The amount of memory that will fit in the sphere will be proportional to the cube of the radius - r³. In reality, computers are quite flat. This is partly a question of form factor and partly a question of cooling. Maybe someday we will learn how to build and cool three-dimensional memory blocks, but for now the practical limitation of the amount of information N within the radius r will be N ∝ r². This is also true for very distant repositories, such as data centers (which are distributed over a two-dimensional surface of the planet).

But is it possible, theoretically, to improve the picture? To do this, learn a little about black holes and quantum physics!

Theoretical boundary

The amount of information that can be placed in a sphere of radius r can be calculated using the Bekenstein boundary . This amount is directly proportional to the radius and mass: N ∝ r · m. How massive can a sphere be? Well, what is the densest in the universe? Black hole! It turns out that the mass of a black hole is proportional to the radius: m ∝ r. That is, the amount of information that can be placed in a sphere of radius r is N ∝ r². We came to the conclusion that the amount of information is limited by the area of ​​the sphere, and not the volume!

In short: if you try to shove a very large L1 cache into the processor, it will eventually collapse into a black hole, which will prevent the user from returning the result of the calculation.

It turns out that N ∝ r² is not only practical, but also a theoretical border! That is, the laws of physics set a limit on the speed of access to memory: in order to get N data bits, you need to transmit a message at a distance proportional to O (√N). In other words, every 100-fold increase in the task leads to a 10-fold increase in the time it takes to access one element. And this is exactly what our experiment showed!

A bit of history

In the past, processors were much slower than memory. On average, a memory search was faster than the calculation itself. A common practice was to keep in memory tables for sines and logarithms. But times have changed. Processor performance grew much faster than memory speed. Modern processors most of their time just waiting for the memory. That is why there are so many cache levels. I believe that this trend will continue for a long time, so it is important to rethink old truths.

You can say that the whole essence of Big-O is in abstraction. It is necessary to get rid of such details of the architecture as a memory delay. This is true, but I argue that O (1) is an incorrect abstraction . In particular, Big-O is needed for abstraction of constant factors, but memory access is not a constant operation. Neither in theory nor in practice.

In the past, any access to memory in computers was equally expensive, so O (1). But this is no longer the case, and for quite some time. I think it's time to think about it differently, forget about memory access for O (1) and replace it with O (√N).

Effects

The cost of accessing the memory depends on the size that is requested - O (√N), where N is the size of the memory that is accessed with each request. This means that if the same list or table is accessed, the following statement is true:

Pass through the coherent list is O (N√N) operation. Binary search is O (√N). Getting from an associative array is O (√N). In fact, any arbitrary search in any database is at best O (√N).

It is worth noting that the actions performed between operations are important. If your program works with a memory of size N, then any random request to memory will be O (√N). So the pass through the list of size K will cost O (K√N). When re-passing (immediately, without recourse to another memory) cost will be O (K√K). Hence an important conclusion: if you need to access the same memory area several times, then minimize the intervals between calls .

If you make a pass through an array of size K, then the cost will be O (√N + K), because only the first call will be arbitrary. The second pass will be O (K). Hence another important conclusion: if you plan to make a pass, then use an array .

There is one big problem: many languages ​​do not support real arrays. Languages ​​like Java and many scripting languages ​​store all objects in dynamic memory, and the array there is actually an array of pointers. If you pass through such an array, then the performance will be no better than when passing through a linked list. Passing through an array of objects in Java is O (K√N) . This can be compensated by creating objects in the correct order, then the memory allocator, I hope , will place them in memory in order. But if you need to create objects at different times or shuffle them, then nothing happens.

Conclusion

Memory access methods are very important. One should always try to access memory in a predictable way, and minimize arbitrary memory accesses. There is nothing new here, of course, but it is worth repeating. I hope you will adopt a new tool for thinking about the cache: memory access costs O (√N). The next time you evaluate the complexity, think about this idea.