The logic of consciousness. Part 4. The secret of brain memory

When something happens to us, our brain captures it, creating memories. Changes that occur in this case with the brain are usually called engrams or traces of memory.

It is quite natural that understanding how the traces of memory look is the main question of studying the brain. Without this, it is impossible to build any biologically reliable model of his work. Understanding the structure of memory is directly related to understanding how the brain encodes information and how it operates on it. All this while, is an unsolved mystery.

An even greater intrigue in the riddle of memory is made by research on the localization of memories. In the first half of the twentieth century, Karl Lashley set very interesting experiments. First, he trained the rats to find a way out in the maze, and then he removed various parts of the brain with them and again started into the same maze. So he tried to find the part of the brain that is responsible for the memory of the acquired skill. But it turned out that the memory was preserved each time, despite the sometimes significant motility disorders. Rats always remembered where to look for a way out and stubbornly strove for it.

')
These experiments inspired Carl Pribram to formulate a popular theory of holographic memory. In accordance with it, like an optical hologram, each specific memory is not located in any one place of the cortex, but is present in each of its places and, accordingly, each place of the cortex stores all memories at once.

At one time, very high hopes in search of engrams were associated with synaptic plasticity. The ability of synapses to change their sensitivity gave hope that through this it is possible to describe all the mechanisms of memory. The idea of synaptic plasticity led to the creation of artificial neural networks. These networks have shown how a neuron can learn to learn something in common with a collection of memories. But finding out the general is not at all the same as storing individual memories.

If you are not directly involved in neuroscience, then most likely you have the impression that neurobiologists have many theories about memory, but apparently there is no certainty which of them is true. And since, most likely, these theories are very complex, they are not particularly talked about in popular literature. So, still, surprisingly it sounds, there is not a single theory of memory. That is, there are different assumptions about what may be associated with memory. But there are no models that would somehow explain how the engrams look and how they work.

At the same time, enormous knowledge has been accumulated about the biology of neurons, about the manifestations of memory, about the molecular processes associated with the formation of memories, and the like. But the deepening of knowledge does not simplify the situation, but only complicates it. So far, not much is known about the subject of research, it is convenient to fantasize. Flight of fancy is not very limited by the framework of knowledge. But as more and more new facts become known, many hypotheses disappear by themselves. To invent new ones that would be in agreement with the facts becomes more difficult.

When such a situation occurs in science, this is a sure sign that somewhere in the very beginning of the argument a fatal error has crept in. At one time, Aristotle formulated the laws of motion. He proceeded from what he saw before him. Aristotle said that there are two types of movement: natural movement and forced movement. Natural motion, according to Aristotle, is inherent only in celestial matter and only celestial bodies can move without the application of force. All other “earthly” bodies require movement of force for movement, otherwise any movement must cease sooner or later. For almost two thousand years this was considered an obvious truth, since everyone else saw the same thing before them. But at the same time, for some reason, for all these two millennia, no one managed to build a single workable theory that would go further than Aristotle’s statements. And only when Galileo and Newton pointed out Aristotle’s annoying mistake that, he says, he forgot about the force of friction, it turned out to be possible to formulate the laws of mechanics known to us. Then, however, was Einstein, but that's another story.

It seems to me that such a “forced movement”, now, is a “grandmother's neuron” in neuroscience. In fact, all the main difficulties with the construction of a memory theory are related to the fact that it is very difficult to link a specific neuron, if we assign to it the functions of a detector of any property, and memory, which, for many reasons, should not be strictly tied to a specific neuron .

Next, I will show how engrams can look for the case when neurons lose their “grandmother's” inclinations.

In the previous sections, a cellular automaton consisting of homogeneous elements was described. When any pattern of activity is created at any place of this automaton, the wave front diverges from this place. In each place of this front, a unique specific pattern arises, only for this wave pattern.

If you remember which picture creates a wave, passing through any place, then you can then reproduce the same picture in the same place and launch a new wave from this place. In each place that this new wave passes on its way, it will repeat the pattern of the original wave.

If you compile a dictionary consisting of a finite number of concepts, then each concept can be associated with its own unique wave. Then, at any place of the automaton, it will be possible to determine what concept this wave propagates by the pattern of the passing wave. And from any place it will be possible to start a wave of any concept if we reproduce in this place a fragment of the pattern of the wave we need.

Flat avomat can be given volume.

The passage of a wave in a small cylindrical volume will then look as shown in the figure below.

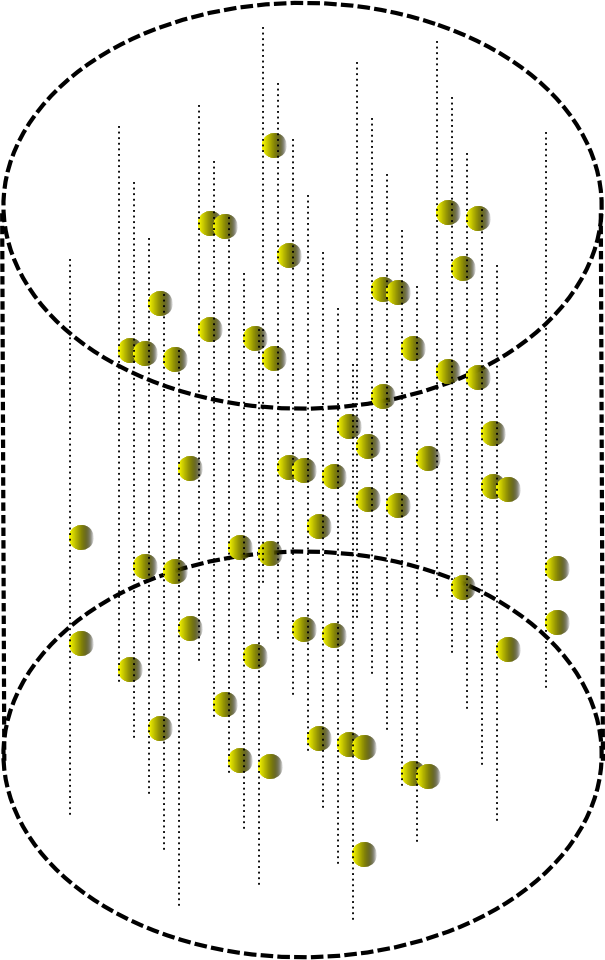
If you start in the machine information wave, and then run the wave ID. So you can remember the picture of the conditional “interference” of these waves. To do this, in each place of the automaton by the elements along which the information wave has passed, one must remember the pattern of the identifier wave surrounding them. This procedure allows you to remember a pair of "key - value". If you later launch a wave of memory identifier into the machine, then the elements of the machine will reproduce the pattern of the informational wave of the memory itself.

You can remember the information key-value pair, both selectively in any small area of the machine and globally throughout the space of the machine. With global memorization information is repeatedly duplicated over the entire area of the machine.

When an informational description does not consist of a single concept, but of several, then such a description can be transmitted along the automaton by successively spreading the information waves of these concepts.

In each fixed volume of the automaton, the passage of a series of waves will cause a change of patterns, each of which can be written with a binary vector. If in the description the sequence of concepts is unimportant, then for one place of the automaton binary vectors created by different waves can be logically bit-wise folded and get a total description vector. This total vector with sufficient bit width saves all the information about its concepts.

The total vector has a high bit depth and contain a large number of units. You can reduce the number of units and lower the width of the total vector by calculating a hash function for it.

The identifier of a memory, like the description itself, may consist of several concepts. Then for him, you can calculate the corresponding hash. When memorizing can be used not source codes, and the resulting hashes.

It was previously shown that for a real brain, possible candidates for the role of elements of a cellular automaton may be sprigs of dendritic neuron trees.

Neuron computation of the hash function of dendritic signals

Dendritic twigs form a dendritic tree (picture below). The branches have only paired branches and do not form closed cycles.

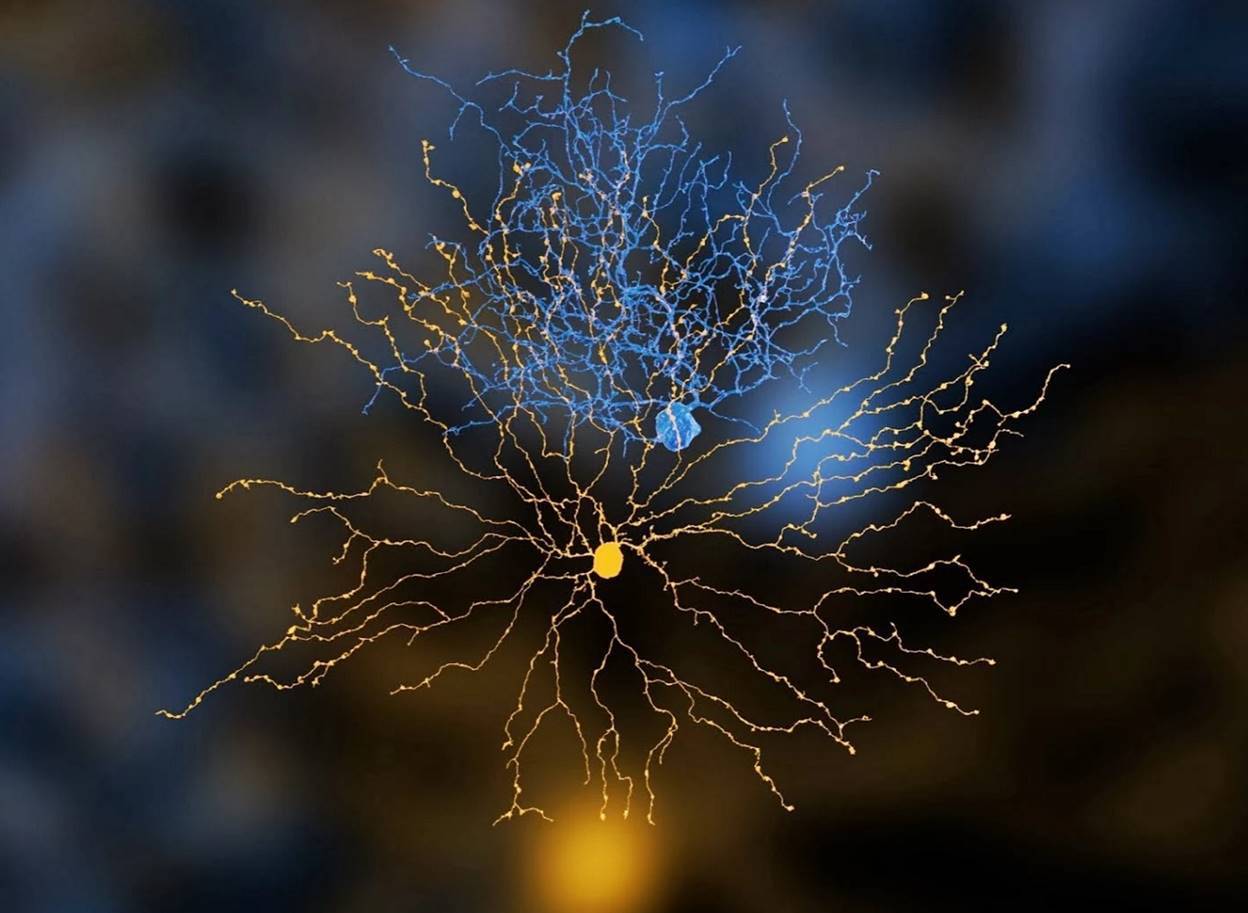
Real Neuron Models (EyeWire Project)

A neuron spike occurs when the depolarization of the membrane on its body in the region of the axon mound reaches a critical value. The depolarization of the soma, that is, the body of the neuron, is mainly due to signals from dendritic branches. Potentially, such signals can be currents arising in dendritic branches and dendritic spikes.

Due to the fact that on the way to the soma, the signals of different branches in the branch points interact with each other, the signals that reach the neuron bodies turn out to be certain functions of the signals of the dendritic branches. The membrane potential of the neuron body itself is a function of the signals of all the branches of its dendritic tree. This, incidentally, is not particularly contrary to the classical concept of a formal neuron. With the proviso that the classic formal neuron is a simple threshold adder of signals at synapses, and we are talking about a rather clever function of signals from dendritic twigs.

In the described interpretation, the spike of one neuron can be safely called the binary result of the hash transformation over the signals of its dendritic branches. Thus, we can say that the whole picture of the activity of neurons can be interpreted as the result of the hash transform of the activity of the dendritic segments.

To activate a neuron, all activity that occurs on a dendritic tree must be packed in a small time interval of several milliseconds. If we assume that a total picture of dendritic activity is formed over such an interval, which occurs after passing through all the waves of a complex description, then neuronal spikes are ideally suited to the role of a hash associated with the picture that has arisen on dendritic segments.

To memorize patterns through interference, two waves are necessary: an identifier wave and a value wave, that is, information stored. In a real crust, these waves can propagate simultaneously. At the same time, the identifier itself can be quite a complex description. It can be assumed that in the cortex, the hash for information and the hash for the identifier can be formed simultaneously, but by different neurons. In principle, these neurons can be different types of neurons. The most common neurons in the cortex are pyramidal and stellate neurons. It may turn out that, for example, the activity of pyramidal neurons encodes a hash function for information, and the activity of star-shaped hash function for memory identifiers.

Dendrite Selected Points

We came to the conclusion that in each place of the cortex current information can be encoded by a combination of the activity of neurons located in this place. In this case, the cumulative instantaneous picture of their spikes can be perceived as a hash function from the dendritic activity corresponding to these neurons.

In the cellular automaton, it was required for memorization that each element of the automaton saw and could memorize a fragment of the hash code of sufficient length. The identifier wave indicated which elements should be memorized, and a series of information waves formed a total picture of the activity of the elements from which the same hash code was obtained, which they should have memorized.

In analogy with the brain, this means that each dendritic branch must see the activity of the surrounding neurons and must be able to selectively remember it.

If we consider that we want one branch to remember not one and not two, but thousands or millions of different combinations of neuron activity, the task becomes very interesting.

Until now, we mainly talked about dendritic neuron trees, now let's look at their axons. So, the main percentage of cortical neurons is in pyramidal and stellate neurons. The axons of these neurons are characterized by strongly branched collaterals. Most of the synaptic contacts of the axon fall on the volume, the dimensions of which are comparable with the size of the dendritic tree (figure below). This geometry of the axon ensures that the signal about the activity of a neuron becomes available to almost all dendritic branches of this and other neurons located in a certain neighborhood (radius of about 50-70 microns) of this neuron.

The structure of a stellate neuron, ruler - 0.1 mm (Braitenberg, 1978)

The availability of a signal should be understood in the sense that for each dendritic branch nearby it will be a neuron where the axon of this neuron will pass near it. Accordingly, at the time of neuron activity, a spike spreads along its axon and neurotransmitters are released from all synapses formed by the axon. Some of these neurotransmitters due to spilover, that is, release beyond the synapse, can reach the desired dendritic branch.

In general, axons can spread far along the cortex or beyond. But the main branch of the axon in most cases falls on the space surrounding the neuron itself. The average distance between the synapses on the dendrite is 0.5 microns. The average distance between the synapses on the axon is 5 microns. The number of contacts on dendrites is equal to the number of contacts on synapses. Accordingly, the total length of the axon is 10 times the total length of the dendrite. On the nearest surrounding neuron space accounts for about 6000 of its synapses. This corresponds to an axon length of 3 centimeters. Now, imagine that these 3 centimeters are laid in a sphere with a radius of less than one tenth of a millimeter and you get an idea of the nature of the axon branching. Next to any segment of the dendrite, there is a multitude of axons of neighboring neurons, some of which approach it more than once.

Synapses directly surrounding the dendritic branch, both their own and just nearby, are the sources of extra-synaptic neurotransmitters for this branch. We depict the location of these sources along the conditional dendrite segment (figure below). For this purpose, the sources are compatible with the dendrite, approximately respecting their position along the length of the dendrite. Enumerate the dendrite surrounding the neurons. Then for each source on this branch you can specify the number of the neuron from the surrounding space that controls this source. Each of the neurons of the environment can have several sources controlled by it, randomly distributed over the dendrite. Let us denote the correlation of neurons and sources on the dendritic branch by the vector D with the elements d _i , where each element is the number of the neuron controlling the source.

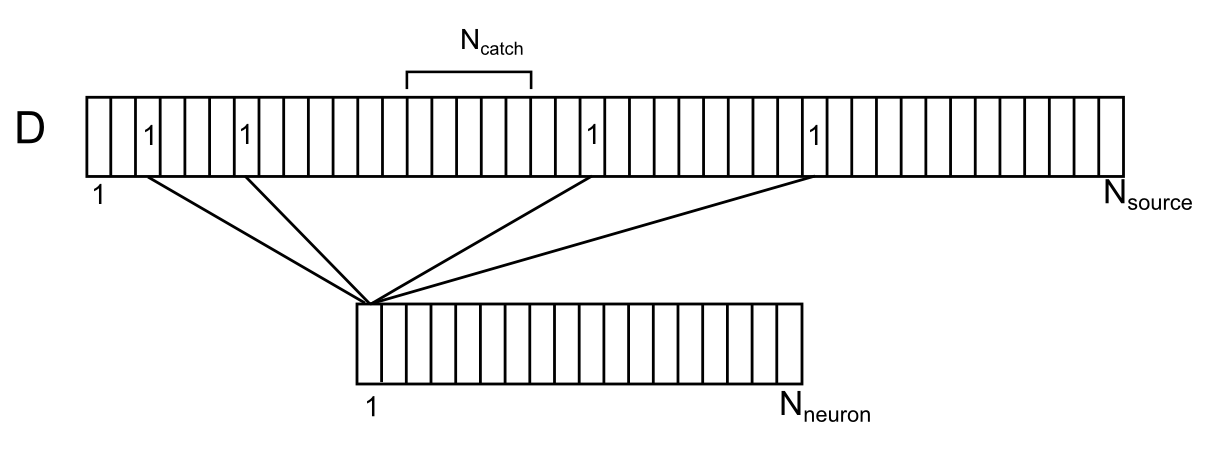
Correlation of surrounding neurons and their contacts on the dendrite

Let N _neuron be the number of environment neurons and N _{source the} number of sources for one dendrite segment.
If we ask the distance to which neurotransmitters spread after spilover, we can determine which synapses are able to influence the chosen place of the dendrite. Let N _{catch the} number of sources capable of influencing the chosen place of the dendrite. For these sources, such a place can be called a "trap".
Now suppose that several neurons from the dendrite environment gave spikes. This can be interpreted as a signal available for observing our dendritic segment. Let N _sig - the number of active neurons that create the information signal. We write this signal with a binary vector S of dimension N _source .
For all positions on the dendrite, except the most extreme ones, you can determine the number of active sources (signal density) that fall into the trap using the formula

For example, for the signal shown in the figure below, the signal density in the marked synaptic trap will be 2 (the sum of the signals from the 1st and 4th neurons).

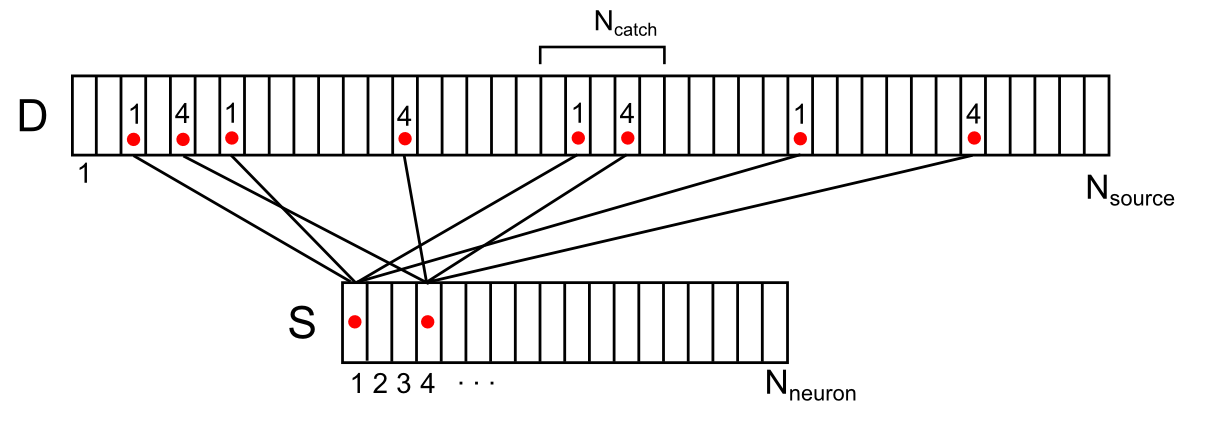
Display of the activity of two neurons of the environment on the dendritic segment (only a part of connections and numbering is shown)

For any arbitrary signal, it is possible to calculate what density distribution it will create on the dendrite. This density will range from 0 to N _catch . The maximum value will be reached when all sources forming the corresponding trap will be active.

We use the values characteristic of the real rat bark (Braitenberg V., Schuz A., 1998) and, based on them, we select the approximate parameters of the model:

Section length = 150 microns (300 synapses, on average 0.5 microns between synapses)
Dendrite dense branching radius = 70 µm
The density of neurons in the cortex = 9x10 ⁴ / mm ³
The number of neurons surrounded by dendrite (N _neuron ) = 100
The number of sources for the dendritic segment (N _source ) = 3000
Trap dimensions (N _catch ) = 15
We assume that the signal is encoded by activity, for example, 10% of neurons, then
N _sig = 10
It is possible to calculate the probability that for an arbitrary signal consisting of N _sig units there will be at least one place on the dendritic segment, where the signal density will be exactly K units. For the given parameters, the probability takes the following values:

The probability table of finding at least one trap with a given density. The first column is the required number of active sources in the trap. The second is the probability of finding at least one place on the dendrite, where there will be just such a number of active sources.

The table shows that with a probability close to 1 on any dendritic segment for any selected volume signal there will be a place in which at least 5 axons of active neurons will converge. This place of the dendrite can be considered chosen in relation to the selected signal. If in this place to remember which axons (synapses) were active, then this will allow, with high accuracy, to detect the repetition of the same signal.

The accuracy of detection is determined by the likelihood of collisions, that is, the probability that the same neurons will be active in any other volume signal, the axons of which converged in the chosen location. That is, if, for example, a signal is determined by the activity of 10 neurons out of 100 and a combination of 5 of these 10 neurons was recorded in a selected location, then for a collision it is enough that in any other signal these 5 neurons also would be active.

Let us denote the number of trapped neurons, that is, the activity of which coincided in the chosen place, through K. In order for another signal consisting of N _sig active neurons to cause erroneous recognition, it is necessary for K of its neurons to coincide with trap neurons. The number of such matching signals -

. The total number of possible signals -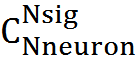

probability of error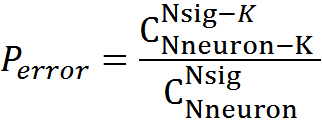

For our model, with K = 5, the probability of detection error will be 3.34x10 ^-6 , with K = 6, respectively, the probability is lower - 1.76x10 ^-7 .

Signal coding at a selected location using a combination of neurotransmitters

Each place of the dendrite is surrounded by synapses, both its own and neighboring dendrites. These synapses are sources of extra-synaptic neurotransmitters. Those of the synapses that are able to influence the chosen place of the dendrite form a trap. The average number of such synapses for an arbitrary dendrite site is N _catch . Let us set the value of K, which determines how many synapses should be active in order to consider the place as chosen with respect to the surround signal. It can be seen that for each place of the dendrite there will be quite a lot of signals that create at this place at least K intersections. So that we can track the repetition of the desired signal with high accuracy, it is necessary not only to fix the fact that in the place chosen for this signal worked To sources, but we must also make sure that these are the sources that correspond to the signal. That is, it is necessary to understand not only how many synapses were activated by the release of neurotransmitters, but to determine which synapses worked this time.

As we have said, for most synapses, at the moment of activity, one “main” neurotransmitter is released and, in addition, one or more neuropeptide (Lundberg, JM 1996. Pharmacol. Rev. 48: 113-178.) (Bondy, CA, et al., 1989. Cell. Mol. Neurobiol. 9: 427-446). The fact of the presence of a large number of neurotransmitters and neuromodulators in neurons of the brain suggests that the main function of such a diversity is to create at the time of synchronous activity of neurons in each place of the space unique combinations of neurotransmitters and modulators. It can be assumed that the additional substances in the synaptic vesicles are distributed over the synapses so as to ensure the maximum diversity in each place of space. If this is the case, then detecting a specific combination of synapse activity comes down to determining the unique set of emitted substances corresponding to these synapses.

Thus, if a detector sensitive to a combination of substances characteristic of this signal is placed in a dendrite position chosen in relation to a certain signal, then the triggering of this detector will with a very high probability of a repetition of the original signal.

Now we know that on every dendritic branch there will always be a place that will be chosen with respect to any signal from surrounding neurons. It remains for us to understand how a dendrite sprig can remember that this chosen place of hers should respond to a certain combination of neurotransmitters.

Neuron receptors like memory elements

Describing the work of the neuron, we said that the surrounding substances affect the work of the neuron through its receptors. Receptors are ionotropic and metabotropic. Ionotropic receptors bind to neurotransmitters released at the synapse, which causes a change in their conformation. The conformation of a molecule is a change in its spatial structure without changing the composition of the molecule itself.

Ionotropic receptors are simultaneously ion channels. A change in conformation opens up the ion channel of the receptor, which leads to the movement of ions and, accordingly, to a change in the membrane potential.

Metabotropic receptors have no ion channels and act differently. The part that is inside the neuron, they are associated with the so-called G-proteins. When these receptors interact with their signaling substances, their conformation changes and the G-protein is released. This leads to various possible consequences. One of the possible consequences is the discovery by G-proteins of neighboring ion channels, which quickly change the local membrane potential of a neuron. That, in turn, causes currents in the dendrite and can cause a dendritic spike.

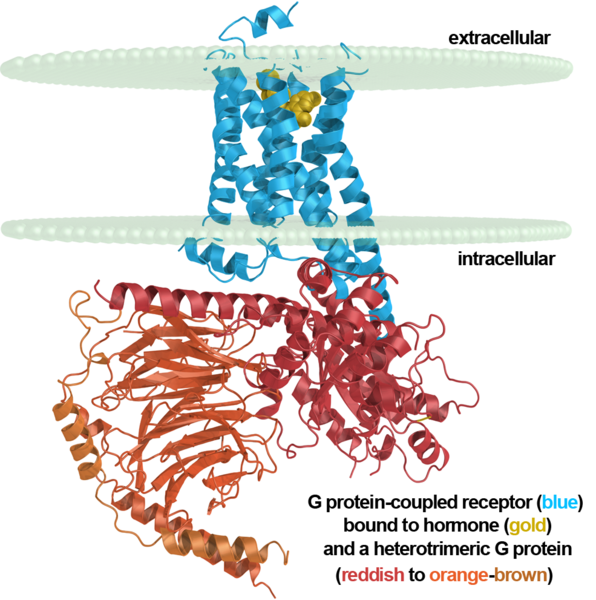
Metabotropic receptor, neuron membrane and G-protein

Metabotropic receptors are mainly located outside the synapses and are targets specifically for extrasynaptic neurotransmitters. Receptors are mainly clustered and act together. Clusters of metabotropic receptors, in fact, are diverse detectors tuned to certain combinations of neurotransmitters.

Clusters of metabotropic receptors are very suitable for the role of elements of the engram for our model. Near each synapse there can be hundreds of such clusters. In them, combinations of receptors are randomly composed in advance, potentially sensitive to many combinations of extrasynaptic neurotransmitters that are possible in this place, that is, neurotransmitters that can be released into the external environment from neighboring synapses.

That is, metabotropic receptors located in large numbers in each place of the dendrite may be “blanks” for future engrams. The transition of “blanks” to engrams can be described as follows. Suppose that the clusters of receptors belonging to a dendritic branch are initially inactive and have no effect on its work. When this branch needs to be memorized, it lets all metabotropic receptors know about it. Such a signal, for example, may be a small total depolarization of the membrane of this branch. As we said above, somewhere on this thread there will definitely be a favorite place. That is, a place where several active synapses will be right next to this branch. If in this place of the branch there is a cluster with receptors, the sensitivity of which coincides with the cocktail of neurotransmitters,then this cluster will have to go to the active state and subsequently always react to the appearance of its own cocktail. If before this cluster did not affect the operation of the dendrite branch, now it will have to create an exciting postsynaptic potential when a cocktail appears.

It turns out that metabotropic receptors really do behave this way. Certain circumstances may immerse the outer and inner portions of the receptor in the membrane, depriving the receptor of sensitivity. Or, conversely, the sensitive parts of the receptor can be pushed out of the membrane. In such a sensitive state, the receptor may remain for some time, then it can return to its original state — this corresponds to short-term memory. The receptor may permanently fix such a sensitive state. If suitable conditions are formed, then the processes of adhesion and polymerization begin, which can leave the receptor in a sensitive state for days and weeks. If the process of fixation, which lasts, presumably, will not be interrupted for about a month, then the state of the receptor will be fixed forever or more correctly to say for life.All this corresponds to different stages of consolidation of long-term memory.

The mechanisms that control this behavior of metabotropic receptors were thoroughly studied and described by A.N. Radchenko (Information mechanisms of the brain, 2007). By the way, Radchenko first suggested that it is the clusters of metabotropic receptors with their conformational transitions that are engram elements.

For memory based on synaptic plasticity, capacitance is considered fairly simple. An example of such a calculation is given in the title picture. Note that in our model, the memory capacity on the dendrites is about 1000 times larger. And that is not all.

In the spatial structure created by the interweaving of axons and dendrites, the ideology of “chosen places” works. That is, in order for the receptors to “be in action” they need not be related to the dendrite to which the synapse belongs, through which the signal is transmitted. Due to the fact that neurotransmitters spread in the intercellular space, “in fact” there can be any receptors that are simply located geometrically nearby. And this, in general, does not necessarily have to be receptors belonging to the neurons.

Thus, glial cells of the cortex, plasma astrocytes (picture below), have sets of the same receptors as neurons, and therefore can be participants of memory mechanisms.

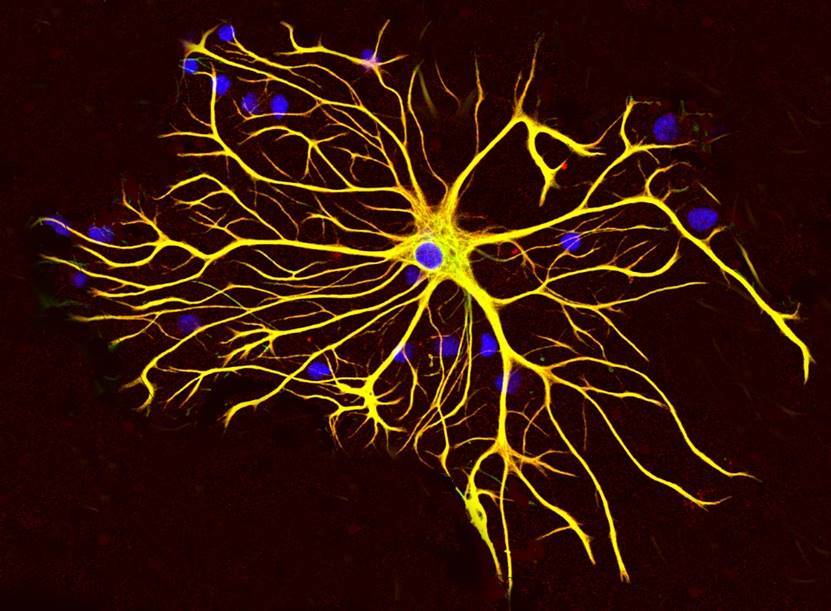
Plasma astrocyte

In the cortex, the number of astrocytes exceeds the number of neurons. Astrocytes of the cortex have short branching processes. These processes cover the nearby synapses (figure below).

Tripartite synapse (RD Fields, B. Stevens-Graham, 2002)

Astrocytes are able to both enhance the synapse response by emitting an appropriate mediator, and weaken it by absorbing it or emitting neurotransmitter-binding proteins. In addition, astrocytes are able to secrete signaling molecules that regulate the release of the neurotransmitter by the axon. The concept of signal transmission between neurons, taking into account the influence of astrocytes, is called a tripartite synapse (RD Fields, B. Stevens-Graham, 2002). It is possible that the trilateral synapse is the main element that implements the mechanisms of mutual work of various memory systems.

The role of the hippocampus. Information in identifiers. Ring Identifiers

In the described memory model, in order for any area of the cortex to form memories, besides the information picture itself, the signals of memory identifiers must be sent to it. Since the zones of the cortex perform different functions, it is appropriate to assume that the identifiers of memories differ for different zones or groups of zones.
Some well-known parts of the brain, due to their specificity, are well suited to the role of source identifiers. Thus, the upper hillocks of the quadrilaterals can be the source of identifiers for visual zones. The lower hillocks of the quadrilateral are suitable for the role of identifier generators for the auditory areas of the cortex. The most representative organ associated with memory is the hippocampus, which is well suited to the role of the key generator of memories for the areas of the prefrontal cortex.

In 1953, a patient who is called HM (Henry Molaison), when trying to cure epilepsy, was performed bilateral removal of the hippocampus (W. Scoviille, B. Milner, 1957). As a result, HM's ability to memorize something completely disappeared. He remembered everything that was with him before the operation, but something new flew out of his head as soon as his attention shifted. Whoever watched the movie “Remember” (“Memento”) by Christopher Nolan, will understand well what the conversation is about.

Henry Molaison

The HM case is quite unique. In other cases, associated with the removal of the hippocampus, where there was no such complete bilateral destruction, as in HM, memory impairment was either not so pronounced or was absent altogether (W. Scoviille, B. Milner, 1957).

Complete removal of the hippocampus makes it impossible to form new memories. Violations of the hippocampus can lead to Korsakov syndrome, which also boils down to the inability to record current events, while maintaining the old memory.

A fairly common idea of the role of the hippocampus is that the hippocampus is a place to hold current memories that are subsequently redistributed over the space of the cortex. In the described model, the role of the hippocampus is different, it creates unique keys of memories.

. . « » . . , , . , . .

, .

In 1971, John O'Keefe opened up cells in the hippocampus (O'Keefe J., Dostrovsky J., 1971). These cells react like an internal navigator. If a rat is placed in a long corridor, then by the activity of certain cells it will be possible to say exactly in which place it is located. Moreover, the reaction of these cells will not depend on how she got into this place.

In 2005, neurons were found in the hippocampus that encoded a position in space, forming something like a coordinate grid (Hafting T., Fyhn M., Molden S., Moser MB, Moser EI, 2005).

In 2011, it turned out that in the hippocampus there are cells that in a certain way encode time intervals. Their activity forms rhythmic patterns, even if nothing else happens around (Christopher J. MacDonald, Kyle Q. Lepage, Uri T. Eden, Howard Eichenbaum, 2011).

Storing data in the form of key-value pairs creates an associative array. In an associative array, the key has a double function. On the one hand, it is a unique identifier that allows you to distinguish one pair from another, on the other hand, the key itself can carry information that greatly facilitates the search. For example, a computer's file system can be considered an associative array. The value is the information stored in the file, the key is the information about the file. File information is the path to the storage location, file name, date of creation. For photos, additional information - geotagging, coordinates of the place where the picture was taken. For music files - album name and artist name. All this file data constitutes complex composite keys that not only uniquely identify filesbut also allow you to search for any of the key fields or any combination thereof. The more detailed the key, the more flexible the search capabilities.

Since the brain implements the same informational tasks as computer systems, it is logical to assume that storing data in the form of key-value pairs by the brain will be accompanied by the creation of keys that are most convenient for searching. For memories that a person deals with, a reasonable set of key descriptors should include:

Indication of the place of action;
Position indication in space;
Specify the time of the event;
A set of concepts that advise the basic meaning of what is happening. Some analogue of the keywords describing the content of the article.

It seems that the hippocampus does not just work with the place, position in space and time, but uses this data to compile complex information keys of memories. At the very least, this explains very well why so diverse functions came together in one place. Moreover, the place directly responsible for the formation of memory.

. , . , . , , (Christopher J. MacDonald, Kyle Q. Lepage, Uri T. Eden, Howard Eichenbaum, 2011). , , .

To describe the course of time, we use the clock and calendar. The basis of both of them are ring identifiers. A minute consists of 60 seconds. This means that 60 identifiers successively replace each other, and after 60 seconds, the first follows again. Similarly, with minutes in an hour, hours in days, days in months, days in weeks, months in years, years in centuries. That is, several ring identifiers with different periodicity allow you to identify any point in time.

Source: https://habr.com/ru/post/309366/

All Articles