Voronoi diagram and its applications
Good all the time of day, dear visitors Habrahabr site. In this article I would like to tell you about what the Voronoi diagram is (shown in the picture below), about the various algorithms for its construction (for 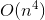 ,
, 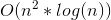 - the intersection of half-planes,
- the intersection of half-planes, 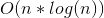 - Forchun's algorithm) and some implementation intricacies (in C ++).
- Forchun's algorithm) and some implementation intricacies (in C ++).

There will also be considered many interesting applications of the chart and some interesting facts about it. It will be interesting!
Article layout:
')
- Required concepts and definitions
- Algorithms of construction
- Applications
- Interesting facts
- References
It should be noted that in this article only algorithms for constructing a Voronoi diagram on a plane will be considered. Along the way, some other algorithms needed to construct a diagram will be considered - an algorithm for determining the point of intersection of two segments, an algorithm O'Rourt the intersection of two convex polygons, an algorithm for constructing a "coastline".
At once I will say that everything that will continue to happen is on the plane .
Well, before you begin to understand what it is - the Voronoi diagram, I recall some concepts of the geometric objects we need (however, it is assumed that you are already familiar with the definitions of point, line, ray, segment, polygon, vertex and edge of a polygon, vector and intuitive notion of plane partitioning):
A simple polygon is a self-intersected polygon. We will consider only simple polygons.
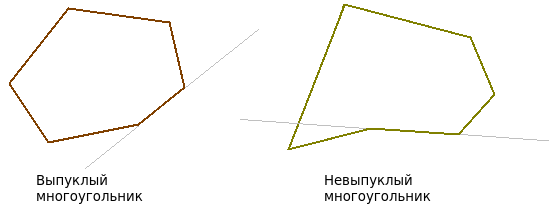
A non-convex polygon is a polygon in which there are two vertices such that through them a line intersects the given polygon somewhere other than the edge connecting these vertices (see the picture),
A convex polygon is a polygon whose extensions of the sides do not intersect its other sides (see picture). Other definitions can be found on Wikipedia .
It is from convex polygons that the diagram will consist. Why precisely convex? Because they are nothing more than the intersection of half-planes (as we will see later), which are convex figures, but why intersection of convex figures is a convex figure, I suggest you find out for yourself (there is evidence, for example, in the book [2] ).
Since I started talking about the half-plane, then you can smoothly go to the diagram itself - it consists of the so-called loci - areas in which there are all points that are closer to a given point than to all the others. In the Voronoi diagram, the loci are convex polygons.
How to build a locus ? By definition, it will be constructed as follows: let given a set of n points for which we build a diagram. Take a specific point p for which we are building a locus, and another point from the given set - q (not equal to p ). Let's draw a segment connecting these two points and draw a straight line that will be the middle perpendicular of this segment. This line divides the plane into two half-planes - in one lies the point p , in the other lies the point q . In this case, the loci of these two points are the resulting half-planes. That is, in order to build a locus of a point p , one must obtain the intersection of all such half-planes (that is, all points of a given set, except p , will be in place of q ).
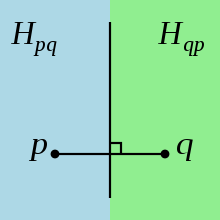
The point for which the locus is built is called the site . In the next picture loci are marked with different colors.

Algorithms for constructing a diagram are precisely nothing more than algorithms for constructing these same loci for all points from a given set. Loci in this problem are also called Voronoi polygons or Voronoi cells .
Finally, we formulate the definition of the Voronoi diagram of n points on a plane (n is natural) —this is a partition of a plane consisting of n loci (for each point along the locus). Again, another definition of the definition can be found on Wikipedia .
By the way, here is a site with an interactive color visualizer of the Voronoi diagram, you can click on the areayourself and stick to see how the diagram is constructed.
If you wonder how the diagram appeared and why it bears the name of Voronoi, then you should look under the spoiler below.
Learn to build a Voronoi diagram. We will look at 4 algorithms, 2 of which in detail (1 with implementation, a full implementation of the Forchun algorithm will be covered in a separate article), 2 more briefly (and without implementation):
After describing some algorithms, its implementation in C ++ will be given. For the implementation we used the SplashGeom © library written by us - a link to github , which has everything necessary for implementing many algorithms of computational geometry on a plane and some in space. Please do not judge strictly this library, it is still under active development and improvement, but all comments will be heard.
If you are interested in other implementations, here are some more:
We now turn to the direct consideration of the algorithms:
The algorithm for constructing the Voronoi diagram "head on" for
Here the idea is to intersect not half-planes, namely, the mid-perpendiculars of the segments (because it is simpler, you should agree) connecting this point with all the other points. That is, following the definition of the Voronoi cell, we will build a locus for point p like this:
The algorithm can also be found on e-maxx.ru .
If you wish, you can independently implement this algorithm using SplashGeom ©. In this article, its implementation is not given, because in practice this algorithm is much inferior to at least the following ...
The algorithm for constructing a Voronoi diagram by intersecting half-planes in
This algorithm can already be used in practice, since it does not have such a large computational complexity. For it we will need: to be able to intersect segments and straight lines, to be able to intersect convex polygons, to be able to intersect half-planes, to be able to combine the obtained loci into a diagram.
The main snag here, I believe, is to realize the normal intersection of convex polygons, because there are unpleasant degenerate cases (coincidence of vertices and / or sides of polygons; if the polygon intersects with itself, it is necessary to think well enough to adapt the O'Rourke algorithm to work correctly in this case).
At once I will say that we limit the whole area of action to the bounding rectangle - the half-planes will cut off the parts from it, which we intersect with each other. This solves the problem of infinite cells in a diagram.
And we need exactly the point of intersection, and not just the definition of its presence. In SplashGeom © this is - for example, the implementation of the intersection of lines and segments:
Now we realize the intersection of polygons. You can certainly do it for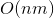 where n and m are the number of vertices of the first and second polygons, respectively — intersect each side of the first polygon with each side of the second, recording intersection points, and also check the points for belonging to another polygon, but we will cross the algorithm to achieve the best speed O`Rourke (original description of the algorithm - [3] ).
where n and m are the number of vertices of the first and second polygons, respectively — intersect each side of the first polygon with each side of the second, recording intersection points, and also check the points for belonging to another polygon, but we will cross the algorithm to achieve the best speed O`Rourke (original description of the algorithm - [3] ).
Also with one of the options for its description can be found on algolist.ru . Our implementation is based on the description of the algorithm in the book [1] (p. 334), with some complementary ideas. Immediately, I note that this implementation does not take into account cases where polygons have common sides (as noted in the book [1] , this case requires separate consideration), however, cases with common vertices work correctly.
Under the spoiler below you can see a general description of the algorithm.
Well, in SplashGeom © it looks like this:
I hope this description and code will be useful to you.
So, we have everything necessary for constructing the intersection of half-planes. Well, let's do it, but let's do it not just, but rationally - due to the associativity of the intersection operation of the half-planes, we can intersect them in any order, which means we intersect two planes, then intersect two more, and then intersect their intersections, because already faster than crossing all separately.
So here it is advisable to use recursion(the mood has immediately spoiled) - her work here is quite understandable, see for yourself:
Now we have the Voronoi polygon of this point, it's time to add it to the chart. There are no problems with this here, because we get the regions in an arbitrary order, and they are not connected to each other (unlike the implementation in the Forchun algorithm, where you can go to the next locus by pointing to an edge):
So, we learned how to build a Voronoi diagram for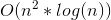 , it has the form of a vector (list) of loci. The disadvantage of this solution is that no information about the neighbors can be obtained (it is possible that this deficiency can be eliminated with an improved implementation).
, it has the form of a vector (list) of loci. The disadvantage of this solution is that no information about the neighbors can be obtained (it is possible that this deficiency can be eliminated with an improved implementation).
Much more information can be obtained from the RSDS ( DCEL ). This structure will be used in the Forchun algorithm.
Next, the Forchun algorithm will be described using a sweeping straight line and a “shoreline”(prepare swimsuits and swimming trunks — go to the beach) In my opinion, this is the most acceptable option if you want to implement the construction of the Voronoi diagram and build it with the "speed" of light. 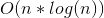 .
.
Forchun's algorithm for constructing the Voronoi diagram
In 1987, Steve Fortune (Steve Fortune) proposed an algorithm for constructing diagrams for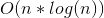 . Of course, it is not the only construction algorithm with such asymptotics, but it is quite understandable and not very difficult to implement (and, moreover, very beautiful
. Of course, it is not the only construction algorithm with such asymptotics, but it is quite understandable and not very difficult to implement (and, moreover, very beautiful and mathematical! ), So I chose it.
Forchun's materials can be found here , here , here and here again .
By the way, the article on Habrahabr was already devoted to the consideration of this algorithm.
So, the basic idea of the algorithm is the so-called sweep line . It is used in many algorithms of computational geometry, because it allows you to conveniently simulate the movement of a straight line over a certain set of objects (for example, the sweep line is also used in the intersection algorithm of n segments).
Before we start talking about how and what we are going to do, let's see how the sweep line moves (taken from here ):

Beautiful, isn't it? In the implementation, everything is approximately the same, only the RFP usually moves from top to bottom, not from left to right, and in fact everything is not so smooth, but it comes from an event to an event (see below), that is, it is discrete .
There are n sites (points on the plane). There is a sweeping line that moves (for example) “from top to bottom,” that is, from the site with the greatest ordinate to the site with the smallest (from event to event, to be exact). Immediately it should be noted that only those sites that are above or on the sweeping line have an impact on the construction of the diagram.
When the RFP reaches the next site (a point event occurs), a new parabola (arch) is created, the focus of which is the site, and the directrix is a sweeping line ( about a parabola on Wikipedia ). This parabola divides the plane into two parts - the “inner” area of the parabola corresponds to points that are now closer to the site, and the “outer” area - to points that are closer to the sweep line, and the points lying on the parabola are equidistant from the site and the RFP. Parabola will vary depending on the position of the RFP to the site - the further the RFP goes down from the site, the more the parabola expands, but at the very beginning it is generally a segment ("directed" up).
Then the parabola expands, it has two control points (break points) - the points of its intersection with the other parabolas ("coastline"). In the “coastline” we store parabolic arcs from one point of intersection with each other to another, and the beach line is obtained. In fact, in this algorithm we model the movement of this “coastline”. because these same break points` move exactly along the edges of the Voronoi cells (after all, it turns out that the control points are equidistant from both sites to which these parabolas correspond, and also from the ZP).
And just at the moment when two control points — one of the different parabolas — “meet”, that is, turn into one, as it were, this point becomes the top of the Voronoi cell (a circle event occurs). at this time, the arc that was between these two points - “collapses” and is removed from the “coastline”. Then we simply connect this point with the previous corresponding one and get the edge of the Voronoi cell.
So, while moving the sweep line down, we meet with two types of events :
The event point is the hit of the RFP on one of the sites, so we create a new parabola corresponding to this site, and two break points are added (in fact, first one, and when the arch extends already two) —the intersection points of this parabolas with a coastline (that is, with the front of existing parabolas). It should be noted that in this algorithm the parabola (or rather its part belonging to the “coastline” - arch ) “is inserted into the coastline” only in case of a point event, that is, a new arch can appear only when processing a point event .
By the way, the following pictures show why the unions of such “parabolic pieces” are called the “coastline”.
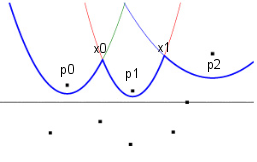

The circle event is the occurrence of a new vertex of the Voronoi cell together with the removal of one arch, because the appearance of a new vertex of the diagram means that there were three arches, left, middle and right, the middle “collapses” due to the convergence of the left and right points of the arches and we get Voronoi diagrams. It is worth noting that in this algorithm the parabola (arch) is removed from the “coastline” only in the event of a circle event, that is, the arch can be removed only when processing a circle event .
There is a theorem that says that the top of the Voronoi diagram always lies at the intersection of exactly three edges of the diagram, and there is a consequence of this theorem, which says that the top of the diagram is the center of a circle passing through three sites and the distance from this point to the sweeping line equal to the radius of this circle (this is a property of points lying on the "coastline"). This is a key moment , because when the lowest point of the circle passing through the three sites lies below or on the sweeping line, we push the event of a circle with this lowest point to the event queue, because when the line hits it, we will get the top Voronoi diagrams.
It is important that one specific arch is connected with any event (point or circle), and vice versa. This is useful when handling events. You should also not forget that you need to add edges to the RSDS ( DCEL ) in time (point 1 in the structures, see below), so you need to understand the connection between the arches and the edges.
Thus, the motion of a straight line is discrete — a straight line at any moment in time either at the site or at the lowest point of the circle passing through three sites, the center of which is the new vertex of the Voronoi diagram. Perfectly.
General algorithm :
The implementation of the Forchun algorithm will be discussed in detail in a separate article , but here are some developments that may help in its understanding.
To implement this algorithm, we need several structures (classes), namely:
Having such data structures, we can write an implementation of a general algorithm:
All the logic and complexity in HandlePointEvent () and HandleCircleEvent (), and a separate article will be devoted to them, further I will provide some auxiliary functions that will later help in implementation.
We need to be able to get the intersection of two parabolas (arches), depending on the position of the RFP. The equation of a parabola with a focus at the point x 'and y' and a directrix, whose position along the y axis is equal to l, is given by the following equation (it can be derived):

By the way, the fraction in front of the bracket is the focal parameter of this parabola. From here we can “pull out” the corresponding coefficients of the parabola equation and solve a system of two non-linear equations in a simple way - subtract one from the other, and then we substitute the found roots into the first, we get two points. We are interested in the point that is lower (that is, with a smaller ordinate), because the highest point lies beyond the "coastline". The described actions are reflected in the following code:
When processing a circle event, we will need to determine the center and the lowest point of the circle constructed from the foci of the three arches (sites). There are some analytical algorithms for constructing a circle on three points (by construction, we mean getting its center and radius), in our program this is done so ( thanks to the alguolist ) - we connect the first two points and the second two points with segments. The center lies at the intersection of the middle perpendiculars, the radius is the distance from the center to any of the three points. Quick and beautiful:
The event point is when we pulled PointEvent out of the queue. What is in it? In it there is only a site with which this event is associated.
What do we do when processing it? We add a new arch to the “coastline”, setting up all the “as needed” links in the tree, and checking if a circle event has appeared in one of three possible cases - we need to check all cases in which the new site can participate.
What do we do when adding an arch? We are looking for a place for it in our “shoreline” binary tree (at the x coordinate), then we insert it.
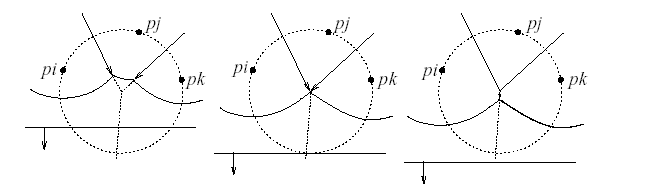
What do we do when inserting? We have found a pointer to the arch, from which the new has an intersection at two points (the case where the intersection point hits exactly one of the control points is considered separately - there the intersection will be with two parabolas - left and right).
That is, we take the arch, which is “broken”, and instead we insert as many as 5 nodes (was 1, became 5, yes) - arch1, bp1, arch2, bp2, arch3. Arch1 is the left piece of the arch that the new intersect crosses, that is, the piece to the left of the left break point, bp1 is the left break point (the left intersection of the new arch), arch2 is the new arch in person, bp2 is the right break point (right intersection of the new arch), arch3 is the right-hand piece of the arch that the new one crosses.
It is worth noting that the point event gives rise to a new edge (or edges, there are cases) of the Voronoi diagram.
One of the possible options for adding a new arch to the “coastline” is presented in this article on Habré , our version is described above, and looks more like the one proposed here .
A circle event is when we pulled CircleEvent from the queue.
What is in it? There is a point in it - this is the lowest point of a certain circle, which passes through three sites, and an arch, which should be removed. There are two control points in the tree and it itself, the control points will eventually turn into one, and the arch must be carefully removed from the tree, rebuilding all the “parent-child connections”. In fact, the processing of this event replaces three nodes in the tree with one (two break points and an arch with one break point).
It is worth noting that the circle event completes two edges of the Voronoi diagram, that is, when processing this event, the edges will be terminated.
I would also say that an important part of event processing is how we monitor the growth of the ribs, adding them to the list and completing the edges, that is, so that in the end they are all “finished” and either are finite or rest on the limiting rectangle.
Since we will get the RSDS ( DCEL ) output , we will be able to get enough information - for each edge we know the corresponding site, we can get a “twin” of this edge, find out the site for it and voila - we recognized our neighbor (this way list, we can create lists of neighbors for all sites, and this is an achievement, since everything happened as a result of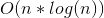 +
+  =
= 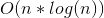 ).
).
And if the edge has a “zero” site, then we are on the “boundary site” - a site with an “infinite” locus. Hmm, but this will allow us to build a convex hull of the initial set of points for in the end, great.
in the end, great.
Well, in general, RSDS is, in fact, a graph, so you can continue to work with this list in many algorithms on graphs.
Recursive Voronoi diagram generation algorithm
This algorithm is given in book [1] (p. 260), here I will give only the construction algorithm itself, since we did not implement this option, although it is a good analogy to the Forchun algorithm.
The general description of the algorithm is not complicated, but the algorithm has its own subtleties, which you can find in this book.
An exhaustive list of all applications of the Voronoi diagram is here , I will mention some of them that seemed to me the most interesting (many of the information is taken from [1] ):
In computational geometry, the Voronoi diagram is needed first of all to solve the problem of proximity of points, or rather, a special gain is given in the solution of the problem ALL closest neighbors(not those that loudly turn on music, but though) , because the methods similar to it are not so simple ( [1] ). Using the Voronoi diagram, you can construct a convex hull behind  (look at the "ray" edges, find the sites to which they belong, and include them in the hull).
(look at the "ray" edges, find the sites to which they belong, and include them in the hull).
There is also an important connection between the Voronoi diagram and the Delaunay triangulation , which allows one to construct one after another , because they are dual to each other (we connect adjacent sites with edges, we end up with the Delone triangulation - wiki considerations ).
, because they are dual to each other (we connect adjacent sites with edges, we end up with the Delone triangulation - wiki considerations ).
An example of using the Voronoi diagram in game development can be found, for example, in this article - here the navigation system in the game engine is based on a diagram.
It is possible, and even likely, that different geolocation software uses Voronoi diagrams. Geolocation recommender systems can use the Voronoi diagram to determine, for example, the nearest grocery store, for various searches and location analyzes.
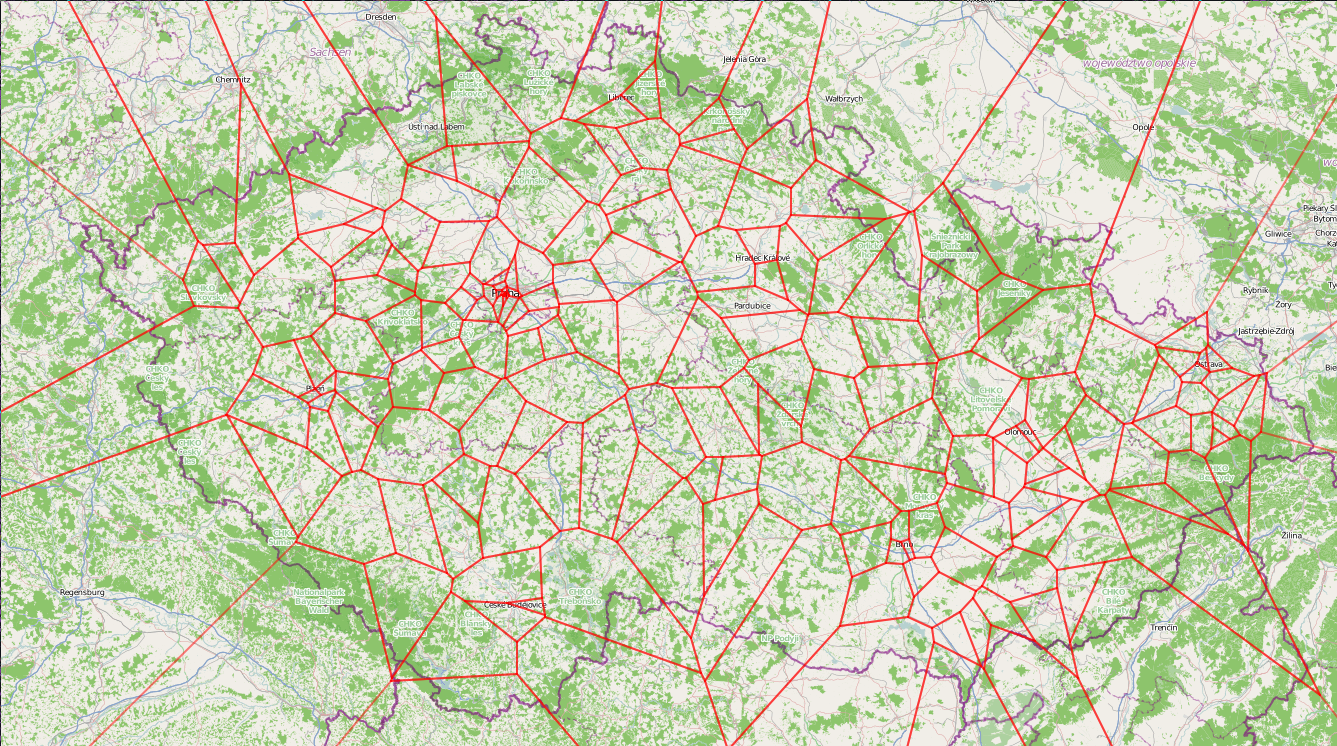
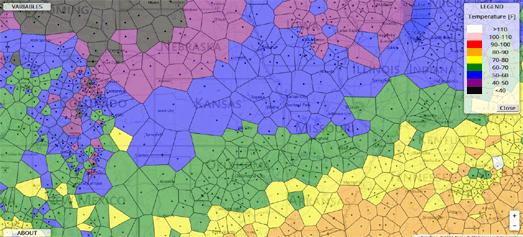
Here you can also mention the use of charts in cartography - for delineating the boundaries of regions and further analysis based on them. Anyway, any geographic diagrams showing the distribution of something can be clearly illustrated using colored Voronoi diagrams, and there we will see a transition of the indicator we need (for example, temperature):
And, of course, you can make various filter photo handlers using the Voronoi diagram, getting a certain “mosaic”.

But this is only the beginning of its application.
It is quite logical that people came up with the idea of using the Voronoi diagram in architecture and design, since it is in itself a beautiful pattern, a kind of “geometric web”, so there are many cases of using it as one of the main elements of a composition or even a frame of all creation. Examples:




From [1] :
In this article, the 3D Voronoi diagram is not considered, but it has many applications in physics and 3D modeling of objects. Various types of grids (and skeletons ) of objects in space can be constructed using the Voronoi diagram (but more often using the Delaunay triangulation ).


3D scanning (and computer vision (computer vision) ) of various objects can also use the Voronoi diagram and Delaunay triangulation, it is also closely related to robotics - the movement of the robot, taking into account the obstacles in the way.

From [1] :
Here is another interesting article about the use of the Voronoi diagram.
Nature is an amazing thing, because it turns out that the color of a giraffe actually looks like a Voronoi diagram. This is visible to the naked eye:

Also noteworthy is the following observation, which shows that the diagram can be seen even on the leaves of trees:

By the way, a little less than a year ago, one incident was also associated with the Voronoi diagram - here it was used in the New Moscow project logo.

And - finally - a video in which you can see how the diagram appears with the growth of circles with centers in the sites:
Here you can draw an analogy with the spread of fire, which has several fires.
Well, that’s the end of our little journey to a world where everyone knows who is closest to them. I hope you enjoyed this article and you really learned something new, useful and interesting.
Thanks for attention!
[1] Preparate F., Sheimos M. Computational geometry. Introduction (1989)
[2] Alexandrov, A. D., Werner, A. L., Ryzhik, V. I. Stereometry. Geometry in space
[3] Joseph O'Rourke. Computational Geometry in C
»The article was prepared by a first-year student of the FIVT MIPT Zakharkin Ilya .
"In writing libraries have also helped students 1st course FIVT MIPT Kirilenko Elena and Kasimov Hope .
» Yaroslav Spirin helped to test the library .
» Special thanks to the mentors Gadelshin Ilnur and Gafarov Rustam .
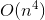 ,
, 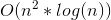 - the intersection of half-planes,
- the intersection of half-planes, 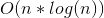 - Forchun's algorithm) and some implementation intricacies (in C ++).
- Forchun's algorithm) and some implementation intricacies (in C ++).
There will also be considered many interesting applications of the chart and some interesting facts about it. It will be interesting!
Article layout:
')
- Required concepts and definitions
- Algorithms of construction
- Applications
- Interesting facts
- References
It should be noted that in this article only algorithms for constructing a Voronoi diagram on a plane will be considered. Along the way, some other algorithms needed to construct a diagram will be considered - an algorithm for determining the point of intersection of two segments, an algorithm O'Rourt the intersection of two convex polygons, an algorithm for constructing a "coastline".
Necessary concepts and definitions
At once I will say that everything that will continue to happen is on the plane .
Well, before you begin to understand what it is - the Voronoi diagram, I recall some concepts of the geometric objects we need (however, it is assumed that you are already familiar with the definitions of point, line, ray, segment, polygon, vertex and edge of a polygon, vector and intuitive notion of plane partitioning):
A simple polygon is a self-intersected polygon. We will consider only simple polygons.
A non-convex polygon is a polygon in which there are two vertices such that through them a line intersects the given polygon somewhere other than the edge connecting these vertices (see the picture),
A convex polygon is a polygon whose extensions of the sides do not intersect its other sides (see picture). Other definitions can be found on Wikipedia .

It is from convex polygons that the diagram will consist. Why precisely convex? Because they are nothing more than the intersection of half-planes (as we will see later), which are convex figures, but why intersection of convex figures is a convex figure, I suggest you find out for yourself (there is evidence, for example, in the book [2] ).
Since I started talking about the half-plane, then you can smoothly go to the diagram itself - it consists of the so-called loci - areas in which there are all points that are closer to a given point than to all the others. In the Voronoi diagram, the loci are convex polygons.
How to build a locus ? By definition, it will be constructed as follows: let given a set of n points for which we build a diagram. Take a specific point p for which we are building a locus, and another point from the given set - q (not equal to p ). Let's draw a segment connecting these two points and draw a straight line that will be the middle perpendicular of this segment. This line divides the plane into two half-planes - in one lies the point p , in the other lies the point q . In this case, the loci of these two points are the resulting half-planes. That is, in order to build a locus of a point p , one must obtain the intersection of all such half-planes (that is, all points of a given set, except p , will be in place of q ).
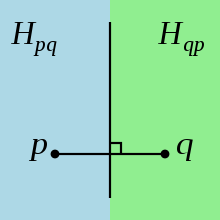
The point for which the locus is built is called the site . In the next picture loci are marked with different colors.

Algorithms for constructing a diagram are precisely nothing more than algorithms for constructing these same loci for all points from a given set. Loci in this problem are also called Voronoi polygons or Voronoi cells .
Finally, we formulate the definition of the Voronoi diagram of n points on a plane (n is natural) —this is a partition of a plane consisting of n loci (for each point along the locus). Again, another definition of the definition can be found on Wikipedia .
By the way, here is a site with an interactive color visualizer of the Voronoi diagram, you can click on the area
If you wonder how the diagram appeared and why it bears the name of Voronoi, then you should look under the spoiler below.
Historical facts
(material taken from this site)
In general, the first use of this diagram is found in the work of Rene Descartes (1596–1650) “Beginning of Philosophy” (1644). Descartes proposed the division of the Universe into zones of the gravitational influence of stars.


Only two centuries later, the famous German mathematician Johann Peter Gustave Lejeune-Dirichlet (1805-1859) introduced diagrams for two- and three-dimensional cases. Therefore, they are sometimes called Dirichlet diagrams.

But already in 1908, the Russian mathematician Georgy Feodosievich Voronoy (April 16 (28), 1868 - November 7 (20), 1908) described this diagram for spaces of higher dimensions, and since then the diagram bears his last name. Here is his brief biography (taken from Wikipedia ):
Georgiy Feodosevich Voronoy was born in the village of Zhuravka, Poltava province (now Chernihiv region). From 1889 he studied at St. Petersburg University from Andrei Markov . In 1894 he defended his master's thesis "On integers that depend on the root of an equation of the third degree." In the same year he was elected a professor at the University of Warsaw, where he studied continued fractions. Voronoi studied Wenceslas Sierpinski . In 1897, Voronoi defended his doctoral thesis "On a generalization of the continuous fraction algorithm", which was awarded the Bunyakovsky Prize.

A bit of history
(material taken from this site)
In general, the first use of this diagram is found in the work of Rene Descartes (1596–1650) “Beginning of Philosophy” (1644). Descartes proposed the division of the Universe into zones of the gravitational influence of stars.


Only two centuries later, the famous German mathematician Johann Peter Gustave Lejeune-Dirichlet (1805-1859) introduced diagrams for two- and three-dimensional cases. Therefore, they are sometimes called Dirichlet diagrams.

But already in 1908, the Russian mathematician Georgy Feodosievich Voronoy (April 16 (28), 1868 - November 7 (20), 1908) described this diagram for spaces of higher dimensions, and since then the diagram bears his last name. Here is his brief biography (taken from Wikipedia ):
Georgiy Feodosevich Voronoy was born in the village of Zhuravka, Poltava province (now Chernihiv region). From 1889 he studied at St. Petersburg University from Andrei Markov . In 1894 he defended his master's thesis "On integers that depend on the root of an equation of the third degree." In the same year he was elected a professor at the University of Warsaw, where he studied continued fractions. Voronoi studied Wenceslas Sierpinski . In 1897, Voronoi defended his doctoral thesis "On a generalization of the continuous fraction algorithm", which was awarded the Bunyakovsky Prize.

Algorithms of construction
Learn to build a Voronoi diagram. We will look at 4 algorithms, 2 of which in detail (1 with implementation, a full implementation of the Forchun algorithm will be covered in a separate article), 2 more briefly (and without implementation):
- Algorithm for constructing a Voronoi diagram "head on." Complexity:
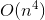 ;
; - Algorithm for constructing a Voronoi diagram by intersecting half-planes. Complexity:
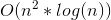 ;
; - Forchun's algorithm for constructing a Voronoi diagram on a plane. Complexity:
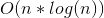 ;
; - Recursive Voronoi diagram building algorithm. Complexity:
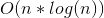 .
.
After describing some algorithms, its implementation in C ++ will be given. For the implementation we used the SplashGeom © library written by us - a link to github , which has everything necessary for implementing many algorithms of computational geometry on a plane and some in space. Please do not judge strictly this library, it is still under active development and improvement, but all comments will be heard.
If you are interested in other implementations, here are some more:
- boost.polygon
- Steve Forchun website
- aewllin / openvoronoi
- Java implementation
- Implementation on JavaScript (there is also a visualizer there)
We now turn to the direct consideration of the algorithms:
The algorithm for constructing the Voronoi diagram "head on" for 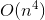
Here the idea is to intersect not half-planes, namely, the mid-perpendiculars of the segments (because it is simpler, you should agree) connecting this point with all the other points. That is, following the definition of the Voronoi cell, we will build a locus for point p like this:
- We obtain the n-1 straight line (median perpendiculars), since we conducted the median perpendiculars of all segments connecting this point p with the rest;
- We intersect in pairs all straight lines, we get
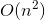 intersection points (because each line can intersect all others, in the “worst case”);
intersection points (because each line can intersect all others, in the “worst case”); - We check all these
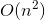 points on the membership of each of the n-1 half-planes, that is, we already get the asymptotics
points on the membership of each of the n-1 half-planes, that is, we already get the asymptotics 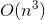 . Accordingly, those points that belong to all half-planes are the vertices of the Voronoi cell of the point p ;
. Accordingly, those points that belong to all half-planes are the vertices of the Voronoi cell of the point p ; - Perform the first three steps for all n points, we get the final asymptotics
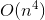 .
.
The algorithm can also be found on e-maxx.ru .
If you wish, you can independently implement this algorithm using SplashGeom ©. In this article, its implementation is not given, because in practice this algorithm is much inferior to at least the following ...
The algorithm for constructing a Voronoi diagram by intersecting half-planes in 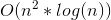
This algorithm can already be used in practice, since it does not have such a large computational complexity. For it we will need: to be able to intersect segments and straight lines, to be able to intersect convex polygons, to be able to intersect half-planes, to be able to combine the obtained loci into a diagram.
Algorithm
- We obtain the n-1 line for the current site (as in the previous algorithm, the perpendicular bisectors). These will be "forming" half-planes;
- Now we have the n-1 half-plane. Each of these half-planes is defined by a straight line from the pre. point and orientation, that is, from which side of the line it is located. The orientation can be determined by the current site for which we are building a locus - it lies in the desired half-plane, and therefore its locus must lie in it;
- We intersect all half-planes - we can do it for
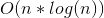 - we get the locus for the current site;
- we get the locus for the current site; - Perform the first three steps for all n points, we get the final asymptotics
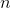 *
* 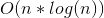 =
= 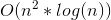 .
.
Implementation
The main snag here, I believe, is to realize the normal intersection of convex polygons, because there are unpleasant degenerate cases (coincidence of vertices and / or sides of polygons; if the polygon intersects with itself, it is necessary to think well enough to adapt the O'Rourke algorithm to work correctly in this case).
At once I will say that we limit the whole area of action to the bounding rectangle - the half-planes will cut off the parts from it, which we intersect with each other. This solves the problem of infinite cells in a diagram.
The intersection of lines and segments
And we need exactly the point of intersection, and not just the definition of its presence. In SplashGeom © this is - for example, the implementation of the intersection of lines and segments:
View code
// // kInfPoint - , kNegInfPoint - Point2D Line2D::GetIntersection(const Line2D& second_line) const { double cross_prod_norms = Vector2D(this->A, this->B).OrientedCCW(Vector2D(second_line.A, second_line.B)); Point2D intersect_point; if (fabs(cross_prod_norms) <= EPS) /* A1 / A2 == B1 / B2 */ { if (fabs(this->B * second_line.C - second_line.B * this->C) <= EPS) /* .. == C1 / C2 */ { intersect_point = kNegInfPoint2D; } else { intersect_point = kInfPoint2D; } } else { double res_x = (second_line.C * this->B - this->C * second_line.B) / cross_prod_norms; double res_y = (second_line.A * this->C - this->A * second_line.C) / cross_prod_norms; intersect_point = Point2D(res_x, res_y); } return intersect_point; } // Point2D Segment2D::GetIntersection(const Segment2D& second_seg) const { Line2D first_line(*this); Line2D second_line(second_seg); Point2D intersect_point = first_line.GetIntersection(second_line); if (intersect_point == kNegInfPoint2D) { if (this->Contains(second_seg.b)) { intersect_point = second_seg.b; } else if (this->Contains(second_seg.a)) { intersect_point = second_seg.a; } else if (second_seg.Contains(this->b)) { intersect_point = this->b; } else if (second_seg.Contains(this->a)) { intersect_point = this->a; } else { intersect_point = kInfPoint2D; } } else if (!(this->Contains(intersect_point) && second_seg.Contains(intersect_point))) { intersect_point = kInfPoint2D; } return intersect_point; } Intersection of convex polygons
Now we realize the intersection of polygons. You can certainly do it for
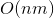 where n and m are the number of vertices of the first and second polygons, respectively — intersect each side of the first polygon with each side of the second, recording intersection points, and also check the points for belonging to another polygon, but we will cross the algorithm to achieve the best speed O`Rourke (original description of the algorithm - [3] ).
where n and m are the number of vertices of the first and second polygons, respectively — intersect each side of the first polygon with each side of the second, recording intersection points, and also check the points for belonging to another polygon, but we will cross the algorithm to achieve the best speed O`Rourke (original description of the algorithm - [3] ).Also with one of the options for its description can be found on algolist.ru . Our implementation is based on the description of the algorithm in the book [1] (p. 334), with some complementary ideas. Immediately, I note that this implementation does not take into account cases where polygons have common sides (as noted in the book [1] , this case requires separate consideration), however, cases with common vertices work correctly.
Under the spoiler below you can see a general description of the algorithm.
I want to know the algorithm O`Rourke!
Algorithm (for additional explanations, refer to the above sources):
The function of the Motion can be implemented in different ways, with us it returns the number (label) of the polygon whose edge we are moving. Conceptually, she does three things inside herself:
- determines the case number - the current relative position of the edge of the first polygon and the edge of the second polygon. This is the main idea of the algorithm - viewing the cases of the position of the ribs relative to each other. All these four positions are well described in [1] , in our implementation the position is determined using the skew product of vectors on the plane;
- determines which edge of a polygon is now “inside”, that is, it lies “to the left” of another edge, in our case this is also verified by skew product (lies “to the left” if the end point lies to the “left”);
- decides whether the current end of one of the edges is written to the intersection polygon. If it fits the right case and the edge is inside, then you need to add, otherwise not.
- Until the maximum number of iterations passes (it is proved that it is not more than 2 * (n + m)), we execute the following instructions:
but). Take the current edges of the first and second polygons;
b). If they intersect, then we consider a point from the intersection: it may be that we just added it to the intersection polygon, then just ignore the addition, otherwise, if it is not the initial intersection point (that is, we have already made a circle), then we add intersection, otherwise we finish the algorithm - we met the intersection point that was at the beginning;
at). Next (regardless of whether the current edges intersect or not) call the Motion function, which is responsible for moving the window of the first (or second) polygon one edge forward, as well as for possible adding a vertex to the intersection polygon. The main actions take place in the Movement . - If there were no intersection points, determine whether one polygon lies inside the other (checking that a point is a convex polygon by O (log (the number of vertices of the polygon)) [1] , pp. 59-60). If it is, then return it, otherwise return an empty intersection.
The function of the Motion can be implemented in different ways, with us it returns the number (label) of the polygon whose edge we are moving. Conceptually, she does three things inside herself:
- determines the case number - the current relative position of the edge of the first polygon and the edge of the second polygon. This is the main idea of the algorithm - viewing the cases of the position of the ribs relative to each other. All these four positions are well described in [1] , in our implementation the position is determined using the skew product of vectors on the plane;
- determines which edge of a polygon is now “inside”, that is, it lies “to the left” of another edge, in our case this is also verified by skew product (lies “to the left” if the end point lies to the “left”);
- decides whether the current end of one of the edges is written to the intersection polygon. If it fits the right case and the edge is inside, then you need to add, otherwise not.
Well, in SplashGeom © it looks like this:
Polygon intersection code
// , Convex2D Rectangle::GetIntersectionalConvex2D(const Point2D& cur_point, const Line2D& halfplane) const { vector<Point2D> convex_points; Segment2D cur_side; Point2D intersection_point; for (int i = 0, sz = vertices_.size(); i < sz; ++i) { int j = (i + 1) % sz; cur_side = Segment2D(vertices_[i], vertices_[j]); intersection_point = halfplane.GetIntersection(cur_side); if (intersection_point != kInfPoint2D) convex_points.push_back(intersection_point); if (halfplane.Sign(cur_point) == halfplane.Sign(vertices_[i])) convex_points.push_back(vertices_[i]); } Convex2D result_polygon(MakeConvexHullJarvis(convex_points)); return result_polygon; } // NumOfCase EdgesCaseNum(const Segment2D& first_edge, const Segment2D& second_edge) { bool first_looks_at_second = first_edge.LooksAt(second_edge); bool second_looks_at_first = second_edge.LooksAt(first_edge); if (first_looks_at_second && second_looks_at_first) { return NumOfCase::kBothLooks; } else if (first_looks_at_second) { return NumOfCase::kFirstLooksAtSecond; } else if (second_looks_at_first) { return NumOfCase::kSecondLooksAtFirst; } else { return NumOfCase::kBothNotLooks; } } // , "" WhichEdge WhichEdgeIsInside(const Segment2D& first_edge, const Segment2D& second_edge) { double first_second_side = Vector2D(second_edge).OrientedCCW(Vector2D(second_edge.a, first_edge.b)); double second_first_side = Vector2D(first_edge).OrientedCCW(Vector2D(first_edge.a, second_edge.b)); if (first_second_side < 0) { return WhichEdge::kSecondEdge; } else if (second_first_side < 0) { return WhichEdge::kFirstEdge; } else { return WhichEdge::Unknown; } } // WhichEdge MoveOneOfEdges(const Segment2D& first_edge, const Segment2D& second_edge, Convex2D& result_polygon) { WhichEdge now_inside = WhichEdgeIsInside(first_edge, second_edge); NumOfCase case_num = EdgesCaseNum(first_edge, second_edge); WhichEdge which_edge_is_moving; switch (case_num) { case NumOfCase::kBothLooks: { if (now_inside == WhichEdge::kFirstEdge) { which_edge_is_moving = WhichEdge::kSecondEdge; } else { which_edge_is_moving = WhichEdge::kFirstEdge; } break; } case NumOfCase::kFirstLooksAtSecond: { which_edge_is_moving = WhichEdge::kFirstEdge; break; } case NumOfCase::kSecondLooksAtFirst: { which_edge_is_moving = WhichEdge::kSecondEdge; break; } case NumOfCase::kBothNotLooks: { if (now_inside == WhichEdge::kFirstEdge) { which_edge_is_moving = WhichEdge::kSecondEdge; } else { which_edge_is_moving = WhichEdge::kFirstEdge; } break; } } if (result_polygon.Size() != 0 && (case_num == NumOfCase::kFirstLooksAtSecond || case_num == NumOfCase::kSecondLooksAtFirst)) { Point2D vertex_to_add; if (now_inside == WhichEdge::kFirstEdge) { vertex_to_add = first_edge.b; } else if (now_inside == WhichEdge::kSecondEdge) { vertex_to_add = second_edge.b; } else { if (case_num == NumOfCase::kFirstLooksAtSecond) vertex_to_add = first_edge.b; // ?! else vertex_to_add = second_edge.b; } if (vertex_to_add != result_polygon.GetCurVertex()) result_polygon.AddVertex(vertex_to_add); } return which_edge_is_moving; } // ( , ) Convex2D Convex2D::GetIntersectionalConvex(Convex2D& second_polygon) { Convex2D result_polygon; size_t max_iter = 2 * (this->Size() + second_polygon.Size()); Segment2D cur_fp_edge; // current first polygon edge Segment2D cur_sp_edge; // current second polygon edge Point2D intersection_point; bool no_intersection = true; WhichEdge moving_edge = WhichEdge::Unknown; for (size_t i = 0; i < max_iter; ++i) { cur_fp_edge = this->GetCurEdge(); cur_sp_edge = second_polygon.GetCurEdge(); intersection_point = cur_fp_edge.GetIntersection(cur_sp_edge); if (intersection_point != kInfPoint2D) { if (result_polygon.Size() == 0) { no_intersection = false; result_polygon.AddVertex(intersection_point); } else if (intersection_point != result_polygon.GetCurVertex()) { if (intersection_point == result_polygon.vertices_[0]) { break; // we already found the intersection polygon } else { result_polygon.AddVertex(intersection_point); } } } moving_edge = MoveOneOfEdges(cur_fp_edge, cur_sp_edge, result_polygon); if (moving_edge == WhichEdge::kFirstEdge) { this->MoveCurVertex(); } else { second_polygon.MoveCurVertex(); } } if (no_intersection == true) { if (second_polygon.Contains(this->GetCurVertex())) { result_polygon = *this; } else if (this->Contains(second_polygon.GetCurVertex())) { result_polygon = second_polygon; } } return result_polygon; } I hope this description and code will be useful to you.
Intersection of half-planes
So, we have everything necessary for constructing the intersection of half-planes. Well, let's do it, but let's do it not just, but rationally - due to the associativity of the intersection operation of the half-planes, we can intersect them in any order, which means we intersect two planes, then intersect two more, and then intersect their intersections, because already faster than crossing all separately.
So here it is advisable to use recursion
View code
Convex2D GetHalfPlanesIntersection(const Point2D& cur_point, const vector<Line2D>& halfplanes, const Rectangle& border_box) { if (halfplanes.size() == 1) { Convex2D cur_convex(border_box.GetIntersectionalConvex2D(cur_point, halfplanes[0])); return cur_convex; } else { int middle = halfplanes.size() >> 1; vector<Line2D> first_half(halfplanes.begin(), halfplanes.begin() + middle); vector<Line2D> second_half(halfplanes.begin() + middle, halfplanes.end()); Convex2D first_convex(GetHalfPlanesIntersection(cur_point, first_half, border_box)); Convex2D second_convex(GetHalfPlanesIntersection(cur_point, second_half, border_box)); return first_convex.GetIntersectionalConvex(second_convex); } } Adding a locus to a chart
Now we have the Voronoi polygon of this point, it's time to add it to the chart. There are no problems with this here, because we get the regions in an arbitrary order, and they are not connected to each other (unlike the implementation in the Forchun algorithm, where you can go to the next locus by pointing to an edge):
View code
// Voronoi2DLocus VoronoiDiagram2D::MakeVoronoi2DLocus(const Point2D& site, const vector<Point2D>& points, const Rectangle& border_box) { Voronoi2DLocus cur_locus; vector<Line2D> halfplanes; for (auto cur_point : points) { if (cur_point != site) { Segment2D cur_seg(site, cur_point); Line2D cur_halfplane(cur_seg.GetCenter(), cur_seg.NormalVec()); halfplanes.push_back(cur_halfplane); } } *cur_locus.region_ = GetHalfPlanesIntersection(site, halfplanes, border_box); cur_locus.site_ = site; return cur_locus; } // VoronoiDiagram2D VoronoiDiagram2D::MakeVoronoiDiagram2DHalfPlanes(const vector<Point2D>& points, const Rectangle& border_box) { Voronoi2DLocus cur_locus; for (auto cur_point : points) { cur_locus = MakeVoronoi2DLocus(cur_point, points, border_box); this->diagram_.push_back(cur_locus); } return *this; } So, we learned how to build a Voronoi diagram for
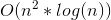 , it has the form of a vector (list) of loci. The disadvantage of this solution is that no information about the neighbors can be obtained (it is possible that this deficiency can be eliminated with an improved implementation).
, it has the form of a vector (list) of loci. The disadvantage of this solution is that no information about the neighbors can be obtained (it is possible that this deficiency can be eliminated with an improved implementation).Much more information can be obtained from the RSDS ( DCEL ). This structure will be used in the Forchun algorithm.
Next, the Forchun algorithm will be described using a sweeping straight line and a “shoreline”
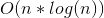 .
.Forchun's algorithm for constructing the Voronoi diagram 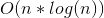
In 1987, Steve Fortune (Steve Fortune) proposed an algorithm for constructing diagrams for
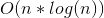 . Of course, it is not the only construction algorithm with such asymptotics, but it is quite understandable and not very difficult to implement (and, moreover, very beautiful
. Of course, it is not the only construction algorithm with such asymptotics, but it is quite understandable and not very difficult to implement (and, moreover, very beautiful Forchun's materials can be found here , here , here and here again .
By the way, the article on Habrahabr was already devoted to the consideration of this algorithm.
So, the basic idea of the algorithm is the so-called sweep line . It is used in many algorithms of computational geometry, because it allows you to conveniently simulate the movement of a straight line over a certain set of objects (for example, the sweep line is also used in the intersection algorithm of n segments).
Before we start talking about how and what we are going to do, let's see how the sweep line moves (taken from here ):

Beautiful, isn't it? In the implementation, everything is approximately the same, only the RFP usually moves from top to bottom, not from left to right, and in fact everything is not so smooth, but it comes from an event to an event (see below), that is, it is discrete .
The essence of the algorithm
There are n sites (points on the plane). There is a sweeping line that moves (for example) “from top to bottom,” that is, from the site with the greatest ordinate to the site with the smallest (from event to event, to be exact). Immediately it should be noted that only those sites that are above or on the sweeping line have an impact on the construction of the diagram.
When the RFP reaches the next site (a point event occurs), a new parabola (arch) is created, the focus of which is the site, and the directrix is a sweeping line ( about a parabola on Wikipedia ). This parabola divides the plane into two parts - the “inner” area of the parabola corresponds to points that are now closer to the site, and the “outer” area - to points that are closer to the sweep line, and the points lying on the parabola are equidistant from the site and the RFP. Parabola will vary depending on the position of the RFP to the site - the further the RFP goes down from the site, the more the parabola expands, but at the very beginning it is generally a segment ("directed" up).
Then the parabola expands, it has two control points (break points) - the points of its intersection with the other parabolas ("coastline"). In the “coastline” we store parabolic arcs from one point of intersection with each other to another, and the beach line is obtained. In fact, in this algorithm we model the movement of this “coastline”. because these same break points` move exactly along the edges of the Voronoi cells (after all, it turns out that the control points are equidistant from both sites to which these parabolas correspond, and also from the ZP).
And just at the moment when two control points — one of the different parabolas — “meet”, that is, turn into one, as it were, this point becomes the top of the Voronoi cell (a circle event occurs). at this time, the arc that was between these two points - “collapses” and is removed from the “coastline”. Then we simply connect this point with the previous corresponding one and get the edge of the Voronoi cell.
Algorithm
So, while moving the sweep line down, we meet with two types of events :
Point event
The event point is the hit of the RFP on one of the sites, so we create a new parabola corresponding to this site, and two break points are added (in fact, first one, and when the arch extends already two) —the intersection points of this parabolas with a coastline (that is, with the front of existing parabolas). It should be noted that in this algorithm the parabola (or rather its part belonging to the “coastline” - arch ) “is inserted into the coastline” only in case of a point event, that is, a new arch can appear only when processing a point event .
By the way, the following pictures show why the unions of such “parabolic pieces” are called the “coastline”.


Circle event
The circle event is the occurrence of a new vertex of the Voronoi cell together with the removal of one arch, because the appearance of a new vertex of the diagram means that there were three arches, left, middle and right, the middle “collapses” due to the convergence of the left and right points of the arches and we get Voronoi diagrams. It is worth noting that in this algorithm the parabola (arch) is removed from the “coastline” only in the event of a circle event, that is, the arch can be removed only when processing a circle event .

There is a theorem that says that the top of the Voronoi diagram always lies at the intersection of exactly three edges of the diagram, and there is a consequence of this theorem, which says that the top of the diagram is the center of a circle passing through three sites and the distance from this point to the sweeping line equal to the radius of this circle (this is a property of points lying on the "coastline"). This is a key moment , because when the lowest point of the circle passing through the three sites lies below or on the sweeping line, we push the event of a circle with this lowest point to the event queue, because when the line hits it, we will get the top Voronoi diagrams.
It is important that one specific arch is connected with any event (point or circle), and vice versa. This is useful when handling events. You should also not forget that you need to add edges to the RSDS ( DCEL ) in time (point 1 in the structures, see below), so you need to understand the connection between the arches and the edges.
Thus, the motion of a straight line is discrete — a straight line at any moment in time either at the site or at the lowest point of the circle passing through three sites, the center of which is the new vertex of the Voronoi diagram. Perfectly.
General algorithm :
- We create a queue (with priority) of events, initially initiating events at a point — a given set of sites (for each site corresponds to a point event);
- While the queue is not empty:
but). We take from it an event;
b). If this is a point event , then we process the point event;
at). If this is a circle event , then we process the circle event; - Finish all remaining edges (work with border_box).
Implementation
The implementation of the Forchun algorithm will be discussed in detail in a separate article , but here are some developments that may help in its understanding.
Required structures
To implement this algorithm, we need several structures (classes), namely:
- RSDS ( DCEL ) - a list for storing the already found edges of the Voronoi diagram;
- Priority queue with events;
- Binary tree (we have this BeachSearchTree) - to store the "coastline" - the current position of parabolas and points. It should be noted that this tree is balanced - the node has either exactly two sons or zero (is a leaf). More information about this structure can be found, for example, in this article on Habré (here it is presented a little differently).
Having such data structures, we can write an implementation of a general algorithm:
View code
VoronoiDiagram2D VoronoiDiagram2D::MakeVoronoiDiagram2DFortune(const vector<Point2D>& points, const Rectangle& border_box) { priority_queue<Event> events_queue(points.begin(), points.end()); shared_ptr<Event> cur_event; BeachSearchTree beach_line; DCEL edges; while (!events_queue.empty()) { cur_event = make_shared<Event>(events_queue.top()); shared_ptr<const PointEvent> is_point_event(dynamic_cast<const PointEvent *>(cur_event.get())); if (is_point_event) { events_queue.pop(); beach_line.HandlePointEvent(*is_point_event, border_box, events_queue, edges); } else { shared_ptr<const CircleEvent> is_circle_event(dynamic_cast<const CircleEvent *>(cur_event.get())); events_queue.pop(); beach_line.HandleCircleEvent(*is_circle_event, border_box, events_queue, edges); } } edges.Finish(border_box); this->dcel_ = edges; return *this; } All the logic and complexity in HandlePointEvent () and HandleCircleEvent (), and a separate article will be devoted to them, further I will provide some auxiliary functions that will later help in implementation.
Secondary functions
Crossing Parabolas (arches)
We need to be able to get the intersection of two parabolas (arches), depending on the position of the RFP. The equation of a parabola with a focus at the point x 'and y' and a directrix, whose position along the y axis is equal to l, is given by the following equation (it can be derived):

By the way, the fraction in front of the bracket is the focal parameter of this parabola. From here we can “pull out” the corresponding coefficients of the parabola equation and solve a system of two non-linear equations in a simple way - subtract one from the other, and then we substitute the found roots into the first, we get two points. We are interested in the point that is lower (that is, with a smaller ordinate), because the highest point lies beyond the "coastline". The described actions are reflected in the following code:
Parabolic intersection code
pair<Point2D, Point2D> Arch::GetIntersection(const Arch& second_arch, double line_pos) const { pair<Point2D, Point2D> intersect_points; double p1 = 2 * (line_pos - this->focus_->y); double p2 = 2 * (line_pos - second_arch.focus_->y); // is not 0.0, because line moved down if (fabs(p1) <= EPS) { intersect_points.first = this->GetIntersection(Ray2D(*this->focus_, Point2D(this->focus_->x, this->focus_->y + 1))); intersect_points.second = intersect_points.first; } else { // solving the equation double a1 = 1 / p1; double a2 = 1 / p2; double a = a2 - a1; double b1 = -this->focus_->x / p1; double b2 = -second_arch.focus_->x / p2; double b = b2 - b1; double c1 = pow(this->focus_->x, 2) + pow(this->focus_->y, 2) - pow(line_pos, 2) / p1; double c2 = pow(second_arch.focus_->x, 2) + pow(second_arch.focus_->y, 2) - pow(line_pos, 2) / p1; double c = c2 - c1; double D = pow(b, 2) - 4 * a * c; if (D < 0) { intersect_points = make_pair(kInfPoint2D, kInfPoint2D); } else if (fabs(D) <= EPS) { double x = -b / (2 * a); double y = a1 * pow(x, 2) + b1 * x + c1; intersect_points = make_pair(Point2D(x, y), Point2D(x, y)); } else { double x1 = (-b - sqrt(D)) / (2 * a); double x2 = (-b + sqrt(D)) / (2 * a); double y1 = a1 * pow(x1, 2) + b1 * x1 + c1; double y2 = a1 * pow(x2, 2) + b1 * x2 + c1; intersect_points = make_pair(Point2D(x1, y1), Point2D(x2, y2)); } } return intersect_points; } Construction of a circle on three points
When processing a circle event, we will need to determine the center and the lowest point of the circle constructed from the foci of the three arches (sites). There are some analytical algorithms for constructing a circle on three points (by construction, we mean getting its center and radius), in our program this is done so ( thanks to the alguolist ) - we connect the first two points and the second two points with segments. The center lies at the intersection of the middle perpendiculars, the radius is the distance from the center to any of the three points. Quick and beautiful:
View the code for constructing a circle on three points.
Circle::Circle(const Point2D& p1, const Point2D& p2, const Point2D& p3) { Segment2D first_segment(p1, p2); Segment2D second_segment(p2, p3); Line2D first_perpendicular(first_segment.GetCenter(), first_segment.NormalVec()); Line2D second_perpendicular(second_segment.GetCenter(), second_segment.NormalVec()); center_ = first_perpendicular.GetIntersection(second_perpendicular); little_haxis_ = big_haxis_ = center_.l2_distance(p1); } Point event handling
The event point is when we pulled PointEvent out of the queue. What is in it? In it there is only a site with which this event is associated.
What do we do when processing it? We add a new arch to the “coastline”, setting up all the “as needed” links in the tree, and checking if a circle event has appeared in one of three possible cases - we need to check all cases in which the new site can participate.
What do we do when adding an arch? We are looking for a place for it in our “shoreline” binary tree (at the x coordinate), then we insert it.

What do we do when inserting? We have found a pointer to the arch, from which the new has an intersection at two points (the case where the intersection point hits exactly one of the control points is considered separately - there the intersection will be with two parabolas - left and right).
That is, we take the arch, which is “broken”, and instead we insert as many as 5 nodes (was 1, became 5, yes) - arch1, bp1, arch2, bp2, arch3. Arch1 is the left piece of the arch that the new intersect crosses, that is, the piece to the left of the left break point, bp1 is the left break point (the left intersection of the new arch), arch2 is the new arch in person, bp2 is the right break point (right intersection of the new arch), arch3 is the right-hand piece of the arch that the new one crosses.
It is worth noting that the point event gives rise to a new edge (or edges, there are cases) of the Voronoi diagram.
One of the possible options for adding a new arch to the “coastline” is presented in this article on Habré , our version is described above, and looks more like the one proposed here .
Handling a circle event
A circle event is when we pulled CircleEvent from the queue.
What is in it? There is a point in it - this is the lowest point of a certain circle, which passes through three sites, and an arch, which should be removed. There are two control points in the tree and it itself, the control points will eventually turn into one, and the arch must be carefully removed from the tree, rebuilding all the “parent-child connections”. In fact, the processing of this event replaces three nodes in the tree with one (two break points and an arch with one break point).
It is worth noting that the circle event completes two edges of the Voronoi diagram, that is, when processing this event, the edges will be terminated.
I would also say that an important part of event processing is how we monitor the growth of the ribs, adding them to the list and completing the edges, that is, so that in the end they are all “finished” and either are finite or rest on the limiting rectangle.
Small analysis of the result
Since we will get the RSDS ( DCEL ) output , we will be able to get enough information - for each edge we know the corresponding site, we can get a “twin” of this edge, find out the site for it and voila - we recognized our neighbor (this way list, we can create lists of neighbors for all sites, and this is an achievement, since everything happened as a result of
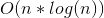 +
+  =
= 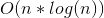 ).
).And if the edge has a “zero” site, then we are on the “boundary site” - a site with an “infinite” locus. Hmm, but this will allow us to build a convex hull of the initial set of points for
 in the end, great.
in the end, great.Well, in general, RSDS is, in fact, a graph, so you can continue to work with this list in many algorithms on graphs.
Recursive Voronoi diagram generation algorithm 
This algorithm is given in book [1] (p. 260), here I will give only the construction algorithm itself, since we did not implement this option, although it is a good analogy to the Forchun algorithm.
Algorithm
- We divide the entire set of sites S into two approximately equal parts (there may be an odd number of points) S 1 and S 2 ;
- Recursively construct Voronoi diagrams for S 1 and S 2 ;
- Combine the resulting diagrams and get a diagram for S.
The general description of the algorithm is not complicated, but the algorithm has its own subtleties, which you can find in this book.
Applications
An exhaustive list of all applications of the Voronoi diagram is here , I will mention some of them that seemed to me the most interesting (many of the information is taken from [1] ):
In programming, game development and cartography
In computational geometry, the Voronoi diagram is needed first of all to solve the problem of proximity of points, or rather, a special gain is given in the solution of the problem ALL closest neighbors
 (look at the "ray" edges, find the sites to which they belong, and include them in the hull).
(look at the "ray" edges, find the sites to which they belong, and include them in the hull).There is also an important connection between the Voronoi diagram and the Delaunay triangulation , which allows one to construct one after another
 , because they are dual to each other (we connect adjacent sites with edges, we end up with the Delone triangulation - wiki considerations ).
, because they are dual to each other (we connect adjacent sites with edges, we end up with the Delone triangulation - wiki considerations ).An example of using the Voronoi diagram in game development can be found, for example, in this article - here the navigation system in the game engine is based on a diagram.
It is possible, and even likely, that different geolocation software uses Voronoi diagrams. Geolocation recommender systems can use the Voronoi diagram to determine, for example, the nearest grocery store, for various searches and location analyzes.

Here you can also mention the use of charts in cartography - for delineating the boundaries of regions and further analysis based on them. Anyway, any geographic diagrams showing the distribution of something can be clearly illustrated using colored Voronoi diagrams, and there we will see a transition of the indicator we need (for example, temperature):

And, of course, you can make various filter photo handlers using the Voronoi diagram, getting a certain “mosaic”.

But this is only the beginning of its application.
In architecture and design
It is quite logical that people came up with the idea of using the Voronoi diagram in architecture and design, since it is in itself a beautiful pattern, a kind of “geometric web”, so there are many cases of using it as one of the main elements of a composition or even a frame of all creation. Examples:




In archeology
From [1] :
In archeology, Voronoi polygons are used to map the range of use of tools in ancient cultures and to study the influence of rival trading centers.- which is quite logical, because usually it is the neighboring regions that fight for any “survival”.
In ecology, the body’s ability to survive depends on the number of neighbors with whom it must fight for food and light.
In modeling and recognition
In this article, the 3D Voronoi diagram is not considered, but it has many applications in physics and 3D modeling of objects. Various types of grids (and skeletons ) of objects in space can be constructed using the Voronoi diagram (but more often using the Delaunay triangulation ).


3D scanning (and computer vision (computer vision) ) of various objects can also use the Voronoi diagram and Delaunay triangulation, it is also closely related to robotics - the movement of the robot, taking into account the obstacles in the way.

In biology and chemistry
From [1] :
The combined effect of electrical and short-range forces, for the study of which complex Voronoi diagrams are constructed, helps determine the structure of molecules.
Here is another interesting article about the use of the Voronoi diagram.
Interesting Facts
Nature is an amazing thing, because it turns out that the color of a giraffe actually looks like a Voronoi diagram. This is visible to the naked eye:

Also noteworthy is the following observation, which shows that the diagram can be seen even on the leaves of trees:

By the way, a little less than a year ago, one incident was also associated with the Voronoi diagram - here it was used in the New Moscow project logo.

And - finally - a video in which you can see how the diagram appears with the growth of circles with centers in the sites:
Here you can draw an analogy with the spread of fire, which has several fires.
Well, that’s the end of our little journey to a world where everyone knows who is closest to them. I hope you enjoyed this article and you really learned something new, useful and interesting.
Thanks for attention!
Bibliography
[1] Preparate F., Sheimos M. Computational geometry. Introduction (1989)
[2] Alexandrov, A. D., Werner, A. L., Ryzhik, V. I. Stereometry. Geometry in space
[3] Joseph O'Rourke. Computational Geometry in C
»The article was prepared by a first-year student of the FIVT MIPT Zakharkin Ilya .
"In writing libraries have also helped students 1st course FIVT MIPT Kirilenko Elena and Kasimov Hope .
» Yaroslav Spirin helped to test the library .
» Special thanks to the mentors Gadelshin Ilnur and Gafarov Rustam .
Source: https://habr.com/ru/post/309252/
All Articles