Interpolation of closed curves
Hello! Recently there was a practical need to use interpolation for closed curves. The project was developed under .Net in C #, and I did not find ready-made implementations of the algorithm, however, as well as for other languages and technologies. As a result, I had to study the material part of the existing methods myself and write my own library. Practices and ready-made solution is ready to share with you.

Search in Google on the topic “interpolation of closed curves” does not give specific results, except for the abstract from the dissertation from 2010 Mr. N. Chashnikov. I took this work as a theoretical basis. I must say that in the process of analyzing mathematics there were difficulties that Nikolai Viktorovich himself helped to solve, for which he thanks a lot! Actually, there will be further analysis of this abstract with specific pieces of code.
So, the task is as follows: at the input there is a set of two-dimensional points, it is necessary to construct an interpolation closed curve.
')
To solve this problem, you can use discrete N-periodic splines with vector coefficients.
Further I will use the following terminology and notation:
Spline poles are a set of reference points (vectors), m is the number of spline poles, n is the number of spline nodes between two adjacent poles, N = n * m is the spline period, r is the spline order.
The first-order B-spline is introduced quite explicitly:

The division by n in the code is explained by the fact that we need to calculate the normalized coefficients, according to the formula:

The calculated coefficients are needed to construct the resulting spline. To do this, use the formula:
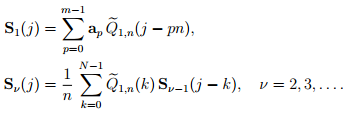 , here v is the spline order, and p is the spline poles.
, here v is the spline order, and p is the spline poles.
Here, for convenience of calculations, the Vector2 class was implemented with the minimum necessary set of methods and operations.
And to ensure the periodicity of the spline, a small method GetPositiveIndex is implemented. Please do not swear because of this, just did not want to make a fuss because of the little things.
Well, actually, this is the whole implementation, which gives us just such a picture:

Stop! What is it?! Spline does not pass through the poles! Bad luck
In order to solve this problem and make an interpolation spline, it is necessary to make a preliminary preparation, namely, use the following formula for recounting the poles, but from a different work .
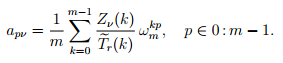


Here a pv are the new poles over which we will carry out all the calculations outlined above, and the last part is the discrete Fourier transform of the m-periodic signal.
Using the formulas above, we achieve the solution of the problem:
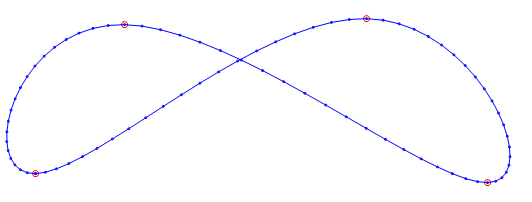

It should be clarified that the order (numbering) of the poles directly affects the appearance of the spline. I leave experiments with n and r to the reader.
In my opinion what you need!
Ps Thanks again to Nikolai Chashnikov for his work and help!
Pps All sources are here .
Search in Google on the topic “interpolation of closed curves” does not give specific results, except for the abstract from the dissertation from 2010 Mr. N. Chashnikov. I took this work as a theoretical basis. I must say that in the process of analyzing mathematics there were difficulties that Nikolai Viktorovich himself helped to solve, for which he thanks a lot! Actually, there will be further analysis of this abstract with specific pieces of code.
Update from Nikolay
Regarding the interpolation of closed curves: you can also use periodic Bezier curves, they were considered at our seminar. There, the result is more traditional, in the form of a trigonometric polynomial, that is, the usual function of a real argument. In some cases, this may be more convenient than discrete splines (which are specified by the function of an integer argument).
So, the task is as follows: at the input there is a set of two-dimensional points, it is necessary to construct an interpolation closed curve.
')
To solve this problem, you can use discrete N-periodic splines with vector coefficients.
Further I will use the following terminology and notation:
Spline poles are a set of reference points (vectors), m is the number of spline poles, n is the number of spline nodes between two adjacent poles, N = n * m is the spline period, r is the spline order.
The first-order B-spline is introduced quite explicitly:
Nothing complicated
/// <summary> /// Q- 1- , /// http://www.math.spbu.ru/ru/mmeh/AspDok/pub/2010/Chashnikov.pdf ( 6). /// </summary> /// <param name="n"> .</param> /// <param name="m"> .</param> /// <returns> Q- 1- .</returns> private static double[] CalculateQSpline(int n, int m) { var N = n * m; var qSpline = new double[N]; for (var j = 0; j < N; ++j) { if (j >= 0 && j <= n - 1) { qSpline[j] = (1.0 * n - j) / n; } if (j >= n && j <= N - n) { qSpline[j] = 0; } if (j >= N - n + 1 && j <= N - 1) { qSpline[j] = (1.0 * j - N + n) / n; } } return qSpline; } The division by n in the code is explained by the fact that we need to calculate the normalized coefficients, according to the formula:
The calculated coefficients are needed to construct the resulting spline. To do this, use the formula:
Implement the calculation
/// <summary> /// , /// http://www.math.spbu.ru/ru/mmeh/AspDok/pub/2010/Chashnikov.pdf ( 7). /// </summary> /// <param name="vectors"> .</param> /// <param name="qSpline"> B- 1- .</param> /// <param name="r"> .</param> /// <param name="n"> .</param> /// <param name="m"> .</param> /// <returns></returns> private static Vector2[] CalculateSSpline(Vector2[] aVectors, double[] aQSpline, int r, int n, int m) { var N = n * m; var sSpline = new Vector2[r + 1][]; for (var i = 1; i <= r; ++i) { sSpline[i] = new Vector2[N]; } for (var j = 0; j < N; ++j) { sSpline[1][j] = new Vector2(0, 0); for (var p = 0; p < m; ++p) { sSpline[1][j] += aVectors[p] * aQSpline[GetPositiveIndex(j - p * n, N)]; } } for (var v = 2; v <= r; ++v) { for (var j = 0; j < N; ++j) { sSpline[v][j] = new Vector2(0, 0); for (var k = 0; k < N; ++k) { sSpline[v][j] += aQSpline[k] * sSpline[v - 1][GetPositiveIndex(j - k, N)]; } sSpline[v][j] /= n; } } return sSpline[r]; } Here, for convenience of calculations, the Vector2 class was implemented with the minimum necessary set of methods and operations.
Here it is - Vector2
/// <summary> /// 2- . /// </summary> public class Vector2 { public double X; public double Y; /// <summary> /// -. /// </summary> public Vector2() { this.X = 0; this.Y = 0; } /// <summary> /// . . /// </summary> /// <param name="x"> .</param> /// <param name="y"> Y.</param> public Vector2(double x, double y) { this.X = x; this.Y = y; } /// <summary> /// . . /// </summary> /// <param name="v"> .</param> public Vector2(Vector2 v) { X = vX; Y = vY; } /// <summary> /// . /// </summary> /// <param name="a"> .</param> /// <param name="b"> .</param> /// <returns> .</returns> public static Vector2 operator +(Vector2 a, Vector2 b) { return new Vector2(aX + bX, aY + bY); } /// <summary> /// . /// </summary> /// <param name="a"> .</param> /// <param name="b"> .</param> /// <returns> .</returns> public static Vector2 operator -(Vector2 a, Vector2 b) { return new Vector2(aX - bX, aY - bY); } /// <summary> /// . /// </summary> /// <param name="a"> .</param> /// <returns> .</returns> public static Vector2 operator -(Vector2 a) { return new Vector2(-aX, -aY); } /// <summary> /// . /// </summary> /// <param name="a"> .</param> /// <param name="d">.</param> /// <returns> .</returns> public static Vector2 operator *(Vector2 a, double d) { return new Vector2(aX * d, aY * d); } /// <summary> /// . /// </summary> /// <param name="d">.</param> /// <param name="a"> .</param> /// <returns> .</returns> public static Vector2 operator *(double d, Vector2 a) { return a * d; } /// <summary> /// . /// </summary> /// <param name="a"> .</param> /// <param name="f">.</param> /// <returns> .</returns> public static Vector2 operator *(Vector2 a, float f) { return a * (double)f; } /// <summary> /// . /// </summary> /// <param name="f">.</param> /// <param name="a"> .</param> /// <returns> .</returns> public static Vector2 operator *(float f, Vector2 a) { return a * (double)f; } /// <summary> /// . /// </summary> /// <param name="a"> .</param> /// <param name="d">.</param> /// <returns> .</returns> public static Vector2 operator /(Vector2 a, double d) { return new Vector2(aX / d, aY / d); } /// <summary> /// . /// </summary> /// <param name="a"> .</param> /// <param name="f">.</param> /// <returns> .</returns> public static Vector2 operator /(Vector2 a, float f) { return a / (double)f; } } And to ensure the periodicity of the spline, a small method GetPositiveIndex is implemented. Please do not swear because of this, just did not want to make a fuss because of the little things.
GetPositiveIndex
/// <summary> /// . /// </summary> /// <param name="j"> .</param> /// <param name="N"> .</param> /// <returns> .</returns> private static int GetPositiveIndex(int j, int N) { if (j >= 0) { return j % N; } return N - 1 + ((j + 1) % N); } Well, actually, this is the whole implementation, which gives us just such a picture:
Stop! What is it?! Spline does not pass through the poles! Bad luck
In order to solve this problem and make an interpolation spline, it is necessary to make a preliminary preparation, namely, use the following formula for recounting the poles, but from a different work .
Here a pv are the new poles over which we will carry out all the calculations outlined above, and the last part is the discrete Fourier transform of the m-periodic signal.
Spline pole counting
/// <summary> /// , . /// http://dha.spb.ru/PDF/discreteSplines.pdf ( 6 7). /// </summary> /// <param name="aPoints"> .</param> /// <param name="r"> .</param> /// <param name="n"> .</param> /// <param name="m"> .</param> /// <returns> .</returns> private static Vector2[] RecalculateVectors(Vector2[] aPoints, int r, int n, int m) { var N = n * m; // . var tr = new double[m]; tr[0] = 1; for (var k = 1; k < m; ++k) { for (var q = 0; q < n; ++q) { tr[k] += Math.Pow(2 * n * Math.Sin((Math.PI * (q * m + k)) / N), -2 * r); } tr[k] *= Math.Pow(2 * Math.Sin((Math.PI * k) / m), 2 * r); } // . var zre = new Vector2[m]; var zim = new Vector2[m]; for (var j = 0; j < m; ++j) { zre[j] = new Vector2(0, 0); zim[j] = new Vector2(0, 0); for (var k = 0; k < m; ++k) { zre[j] += aPoints[k] * Math.Cos((-2 * Math.PI * j * k) / m); zim[j] += aPoints[k] * Math.Sin((-2 * Math.PI * j * k) / m); } } // . var result = new Vector2[m]; for (var p = 0; p < m; ++p) { result[p] = new Vector2(0, 0); for (var k = 0; k < m; ++k) { var d = (zre[k] * Math.Cos((2 * Math.PI * k * p) / m)) - (zim[k] * Math.Sin((2 * Math.PI * k * p) / m)); d *= 1.0 / tr[k]; result[p] += d; } result[p] /= m; } return result; } Final Spline Calculation Method
/// <summary> /// N- . /// </summary> /// <param name="aPoints"> ( ). 2- .</param> /// <param name="r"> .</param> /// <param name="n"> .</param> /// <param name="aIsIncludeOriginalPoints">True - , false - .</param> /// <returns></returns> public static Vector2[] Calculate(Vector2[] aPoints, int r, int n = 5, bool aIsIncludeOriginalPoints = true) { if (aPoints == null) { throw new ArgumentNullException("aPoints"); } if (aPoints.Length <= 2) { throw new ArgumentException(" > 2."); } if (r <= 0) { throw new ArgumentException(" > 0."); } if (n < 1) { throw new ArgumentException(" >= 1."); } var m = aPoints.Length; var N = n * m; Vector2[] vectors; if (aIsIncludeOriginalPoints) { vectors = RecalculateVectors(aPoints, r, n, m); } else { vectors = new Vector2[m]; aPoints.CopyTo(vectors, 0); } var qSpline = CalculateQSpline(n, m); var resultPoints = CalculateSSpline(vectors, qSpline, r, n, m); return resultPoints; } Using the formulas above, we achieve the solution of the problem:
It should be clarified that the order (numbering) of the poles directly affects the appearance of the spline. I leave experiments with n and r to the reader.
In my opinion what you need!
Ps Thanks again to Nikolai Chashnikov for his work and help!
Pps All sources are here .
Source: https://habr.com/ru/post/309210/
All Articles