The logic of consciousness. Part 3. Holographic memory in a cellular automaton

Earlier, we described a cellular automaton in which waves with a cunning inner pattern can appear. We have shown that such waves are able to spread information across the surface of an automaton. It turned out that any place in the automaton can be both a receiver and a source of waves. To receive a wave in any place, it is enough to see what pattern it turns out at the moment of the wave passing. If this pattern is remembered and subsequently reproduced in the same place, a wave will propagate from this pattern, repeating the pattern of the original wave in its path.

All this is very reminiscent of the radio. Anywhere on earth you can take a message and remember. Then from anywhere you can start it on the air again. At the same time, broadcasting does not mean a specific recipient, but the availability of a signal for everyone.

The automaton we describe has memory. More precisely, all its elements have memory. Item memory is specific. The only thing that sees the element of the machine is a pattern made up of the activity of its neighbors. The only way an element can react to a particular pattern is either to become active itself or, on the contrary, to turn off. An element's memory is a set of patterns it has memorized, with an indication of how to react to them: turn it on or off.

Interference patterns in the cellular automaton

The presence of the elements of the automaton's own memory allows the use of the cellular automaton itself as a universal storage device that implements an associative array. An associative array is a repository of key-value pairs. In order to be able to manipulate with the saved data, an associative array must support operations: add a pair, find a pair (by key or by data), and delete a pair. Let us show how this can be implemented in our cellular automaton.
')
For large analogies with the cerebral cortex, we move from a flat cellular automaton to a volumetric one. Arrange the elements in the nodes of a regular spatial lattice. Replace the flat tracking space on the volume, forming a cylinder. We assume that the thickness of the automaton is substantially less than the size of its surface. Let us single out for observation a cylindrical volume whose dimensions are comparable with the tracking area of ​​the elements of the automaton (figure below). We will call a volume of this size elementary, meaning that it is the minimum volume that allows a wave to be launched without fail if a fragment of the pattern of this wave is reproduced inside this volume.


Spatial cellular automaton and a dedicated cylindrical fragment

Suppose that we sequentially launched two information waves in the automaton. Let the first wave bears the value we want to save, and the second wave is the unique key that we want to make an identifier of the stored information. Each of the waves will spread its pattern throughout the entire space of the automaton, that is, in each of its places two patterns will successively pass, formed by the first and second wave, respectively. In the observed fragment, the first wave will leave a mark, for example, such as shown in the figure below.


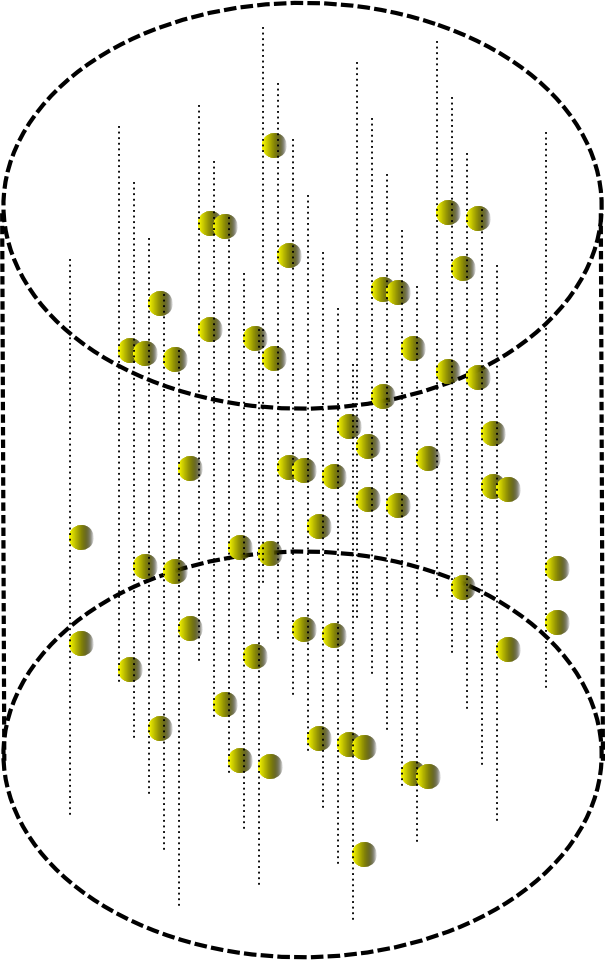
The trace of the information wave carrying the value that you need to remember

Let the elements remember their recent state. That is, after the passage of the wave, the activity of the elements disappears, but the fact that they were active is stored by the elements before the general reset signal. In other words, the trace left by the wave is saved until a general reset.

The second wave will leave its mark in the same volume (figure below). We denote the elements of each wave by our color, while some elements can receive two colors at once.


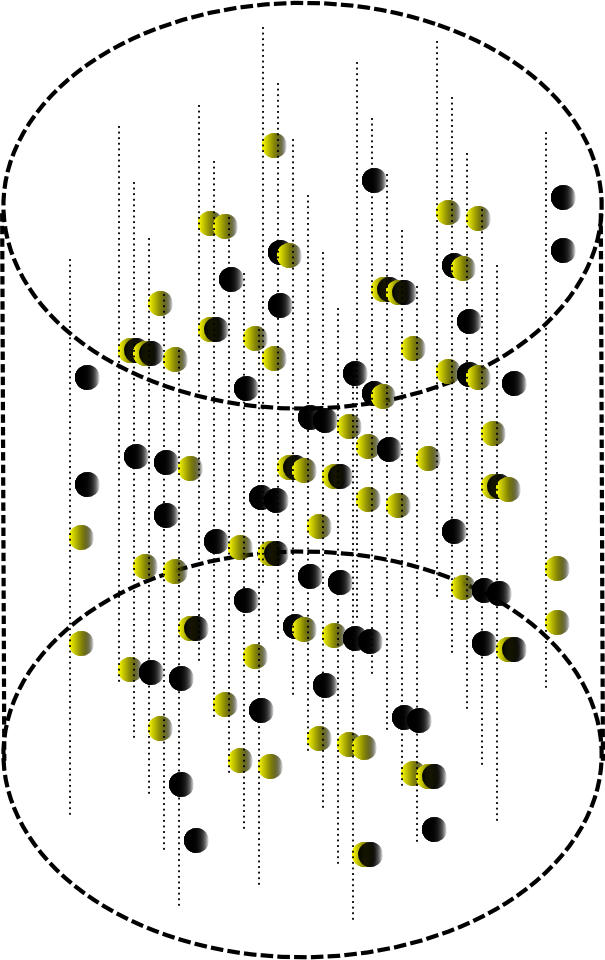
Traces from two waves. Yellow - elements encoding value. Black - key coding elements

Now, let's memorize. To do this, on all the elements of yellow color, remember the pattern formed by the elements of black. In turn, on all black elements we will remember the pattern formed by the yellow elements. The first captures the information pattern with the required key. The second, on the contrary, fixes the key pattern, while the “key” is the information pattern itself. As a result of such a kind of “interference” in the specified volume, the key-value pair will remain.

The process of reverse playback is very simple. Run the key in the machine. That is, we will start the same black wave. In the volume we are following, the yellow elements are activated. For them, the black element pattern will be a signal stored in their memory and causing their activity. As a result, we will restore the yellow pattern, which is the value for the corresponding key. This yellow pattern will trigger a wave that will spread the information extracted from the memory over the space of the machine. Actually, the described is the implementation of the recording of information and its search by key.

If all keys are unique, then reproduction of information by key will cause a single response information wave corresponding to the value of the pair for this key. If the value codes are also unique, then a reverse key search by value will be possible.

To save one information key-value pair, it is enough to perform memorization in one elementary volume. If in any way when memorizing to indicate to the automaton the place where we want to store the memory, then we can get a spatially distributed storage system. However, nothing prevents you from performing “redundant” distributed memorization. That is, to remember one and the same information not in one place, but in the whole space of the cellular automaton. Both that and another - very important properties which will be necessary for us further.

Each elemental volume can store many memories. The size of its memory is proportional to how many patterns a separate element of an automaton can store. If one memorized pattern is, for example, two percent of the activity of all elements, then the total number of possible memories for an elementary volume will be approximately 20-30 times more than the memory of one element.

The peculiar interference of two information waves and distributed memorization make the described mechanism extremely similar to optical holography . Principles of holography discovered and described by Denes Gabor. If we have a light source with a stable frequency, then dividing it by means of a translucent mirror into two, we will get two coherent light fluxes. One stream can be directed to the object, and the second to the photographic plate.


Create a hologram

As a result, when the light reflected from the object reaches the photographic plate, it will create an interference pattern with the stream illuminating the plate. The interference pattern, imprinted on the photographic plate, will save information not only about the amplitude, but also about the phase characteristics of the light field reflected by the object. Now, if we illuminate the previously exposed plate, the original luminous flux will be restored, and we will see the memorized object in all its three-dimensional volume.


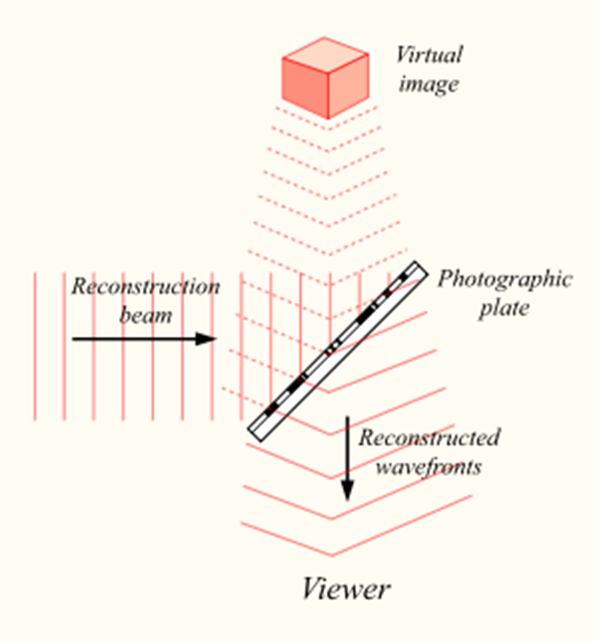
Hologram reproduction

The hologram has several amazing properties. First, the luminous flux saves volume, that is, looking at a phantom object from different angles, you can see it from different sides. Secondly, each area of ​​the hologram contains information about the entire light field. So, if we cut the hologram in half, then at first we will see only half of the image. But when we look at the hologram from the side, then beyond the edge of the remaining hologram we will be able to see the second “cut off” part. The smaller the fragment of the hologram, the lower its resolution, but even through a small area you can, like through a keyhole, view the entire image.

Accordingly, the described memory in its essence may well be called holographic, but with the proviso that it is not based on the classical wave interference, but on the pattern interference that is somewhat different in its algorithm. Although, if we dig deeper, in the view of digital physics , which considers space as a cellular automaton, these interferences can be identical in nature.

Description of the state of the machine through a bitmap

Any elementary volume of the machine can be mapped bitmap. In the initial state, all its elements are zero. The passage of a wave turns part of the elements into units. In the cellular automaton, after passing through the wave front, the elements return to the inactive state. In the mapped bitmap, we introduce some other rules. We will leave the array bits in a single state, accumulating activity after passing the next wave. We will perform a general reset of the state of the array, when we consider it necessary.

Each wave encodes only one concept. Adding traces of waves allows you to make a description, consisting of several concepts at the same time. Resetting the state of the bitmap resets the description. The successive passage of the waves creates a description. The finished description appears when all the necessary waves propagate.

The structure described corresponds to the Bloom filter . Suppose that we have a set C consisting of concepts with which we operate. To each element c _{i of the} set C, we associate a binary code b _{i of} length m, containing k ones. Select the position of units randomly. We compose the set I from several concepts of the set C.

Bloom's filter contains a bitmap B of m bits. In the initial state, it is reset. Adding an element to Bloom's filter is a reference to the unit of those filter elements that correspond to the binary code of the element being added. Mapping the set I to the Bloom filter is equivalent to the logical addition of the binary codes of the elements constituting I, and transferring the resulting code to the binary array of the filter.

The Bloom filter allows you to check the membership of any element of the set C, the set I. To check, you must take the binary code of the element and make sure that all units of the code correspond to the units in the Bloom filter. If at least one of the positions of the filter does not match, then the element is guaranteed not to belong to the set I. If the check is passed, then the element is contained in I with a high probability, which depends on the filter parameters. I The example of the check is shown in the figure below.


Bloom filter. The element w does not belong to the given set {x, y, z}

One concept in a cellular automaton in an elementary volume is encoded by a pattern consisting of a small number of elements with respect to the total number of elements in this volume. Accordingly, the binary code of the concept can be spoken of as a long binary bit code.

After the formation of the bit array corresponding to the long description, the density of units will increase, which will correspond to the long binary medium-low coding.

For our automaton, we assume that the total digit capacity, equal to the number of elements in the elementary volume, is quite high, the total number of concepts used is reasonably limited and that the possible number of concepts in one description is not particularly large. Then it is possible to take a bitmap obtained after transmitting a description consisting of several concepts and restore the original concepts themselves. To do this, you need to try on the bitmap, like the Bloom filter, codes for all possible concepts and see which ones will give a positive result. In the assumptions made, it can be achieved that the probability of false positives is low when checking.

This means that total binary codes can be used as analogues of the original description. That is, in each place of the automaton the total binary code received after the distribution of a complex description will contain the entirety of the original description.

Creating a hash of complex descriptions in the cellular automaton

To save a complex description in its cellular automata in its entirety, it suffices to carry out the memorization procedure described earlier. Create an identifier of memories and implement the description and identifier interference. When memorizing the elements that encode the pattern of the identifier of the memory, you will have to remember a picture of the description containing quite a few units. When computer simulating a cellular automaton, this is not a problem, but, as will be shown later, memorizing with a large number of signals is difficult for a biological system. Accordingly, the question arises: is it possible to reduce the number of active elements that make up the description (or identifier), reducing their number to the amount of low coding?

As a result, we come to the problem of hashing . Hashing is a conversion, according to a certain algorithm, of an input array of data of arbitrary length into an output bit string of fixed length. Such transformations are also called hash functions or “convolution functions,” and their results are called a hash code or “message digest.”

To bring our cellular automaton to the conditions of the hashing task, we introduce a new bit hash array of relatively small length for an elementary volume.

The hash conversion we need should reduce the length of the long binary code to the size of the hash. A good hash function should minimize the number of possible collisions. That is, it is desirable that the likelihood that two different descriptions can get the same hash was minimal.

We will not now dwell on which hash function is better to use in our case. This question is quite interesting, but difficult. Simply, we give, as an example, one of the simplest options.

You can divide the elements of the original bitmap into groups and calculate any one-bit logical function of the elements of the group (figure below). Then generate a hash code of the received bits.


Example of calculating one bit of hash for a group of elements

We introduce into the cellular automaton additional elements that will correspond to the elements of the hash array. We will not affect the regular grid of the source cells. Let's create for our own elements our own lattice located in the same geometric space. Let the old elements of the automaton see the picture of the activity of the surrounding hash elements and let them memorize it.

In addition, we modify the original elements in such a way that they can accumulate information about their activity during those several waves while the message is being transmitted.

Let us try to memorize a complex description consisting of several concepts. For this purpose, we will successively spread the waves, corresponding to the concepts from the description, over the space of the automaton. We accumulate information about the activity. That is, we will form a total picture of the trace of waves in the entire volume of the automaton. Then, we calculate the activity of the hash elements.

The figure below shows the result of the addition of several wave patterns and the result of their hash transform. Green elements form a hash code pattern. These elements exist separately from the original basic elements, but are with them in the same space. That is, they are available for observation.


Addition of several patterns


Hash transform result

Now spread the key and keep the memory. Only now the elements involved in the key pattern will not memorize the informational picture of the activity of the main elements, but the pattern of the resulting hash.

After the recording is completed, we can reset the activity of the machine and re-submit the original description. The pattern of activity of the main elements will be repeated, the hash calculated from it will be repeated. The appearance of a familiar hash code will cause the appearance of the pattern corresponding to the key of the previously made memory.

If the description corresponds to a single event, the automaton can extract and distribute the identifier of this event. If there are several memories in memory with the same descriptions, then a summary picture composed of the identifiers of these descriptions will appear. This situation requires more complex processing.

Let's summarize:

• Two information waves can “interfere” with each other. One wave marks the elements that need to remember something, and the other wave draws a pattern of what exactly they need to remember;
• Too dense pattern when memorizing, you can replace it with a hash;
• You can memorize locally in a small area of ​​the machine. Then you can store something in each place;
• You can remember globally. Then in each place of the machine will be stored its own copy of the same information.

It is not by chance that I focus on the possibilities of local and global memorization. Next, I will show that these two mechanisms are key to understanding the operation of the brain.

Alexey Redozubov

The logic of consciousness. Introduction
The logic of consciousness. Part 1. Waves in the cellular automaton
The logic of consciousness. Part 2. Dendritic waves
The logic of consciousness. Part 3. Holographic memory in a cellular automaton
The logic of consciousness. Part 4. The secret of brain memory
The logic of consciousness. Part 5. The semantic approach to the analysis of information
The logic of consciousness. Part 6. The cerebral cortex as a space for calculating meanings.
The logic of consciousness. Part 7. Self-organization of the context space
The logic of consciousness. Explanation "on the fingers"
The logic of consciousness. Part 8. Spatial maps of the cerebral cortex
The logic of consciousness. Part 9. Artificial neural networks and minicolumns of the real cortex.
The logic of consciousness. Part 10. The task of generalization
The logic of consciousness. Part 11. Natural coding of visual and sound information
The logic of consciousness. Part 12. The search for patterns. Combinatorial space