Vector computing in JS, is there any sense when and how SIMD can be used in the browser

More and more, the field of application of the javascript programming language is moving away from the movement of buttons in the browser and background repainting in the direction of complex and voluminous web applications. Already throughout the whole world, the WebGL technology is striding, which allows displaying three-dimensional scenes in the browser directly in the js language, and with it the tasks become more complex.

The performance of user machines continues to grow, and with it the language acquires new expressive means to speed up computations. And while WebAssembly is somewhere there in the distant and bright future, asm.js is stuck in a swamp and turned off the path, soon as part of es2015, now support JS for separate operations as a standard.

All who are interested in what SIMD and vector calculus are, how to use them in js, as well as what their use gives - I ask for cat.

Deviation from the author: you do not deja vu, this article is really a reloading of the previous one. Unfortunately, then I did not put enough effort to get a quality article, and the tests were not suitable for anything, as a result - I got totally wrong conclusions, which I rightly received criticism for. "Habr cake and every demand here is not a ride," I rejoiced, I figured that my article is still one of the few that pops up on SIMD JS requests and it would be wrong to distribute incorrect information, and even poor quality. In this article I try to correct that ruthlessly hid and removed as a bad dream and an instructive lesson about the ratio of time spent on an article to its quality.

Theory

Suppose you need to perform some simple operation with each element from the array. Take a sum with a constant C, write an example in C

int arr[16] = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15}; const c = 5; for (int i = 0; i < 16; i++) { arr[i] = arr[i] + c; } 

Doggy people can try to optimize this example a little by writing something like:

 int arr[16] = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15}; const c = 5; for (int i = 0; i < 16; i += 4) { arr[i] = arr[i] + c; arr[i + 1] = arr[i + 1] + c; arr[i + 2] = arr[i + 2] + c arr[i + 3] = arr[i + 3] + c; } 

Optimization is dubious, but, in fact, work. The reason for this is not that we do the operation i = i + 1 much less often; (after all, it all the same happens when taking the index), and the fact that the processor in this case can load and perform operations with large overlapping on each other in the pipeline, as long as the operations do not depend on each other, which allows it to perform internal operations, up to performing these operations simultaneously and batch loading the next part of the array.

The problem is that he can make these optimizations, and he may not. We cannot explicitly influence this, but the lining is still preserved. And if the sum is calculated quickly, then some square root is already performed for a sufficiently noticeable time so that there is a desire to force the processor to perform this operation simultaneously for several numbers.

Something like this was thought many years ago (in the 70s) somewhere in the bowels of Texas Instruments and CDC, having made the first vector super-computers. However, before them, a certain Michael Flynn proposed his taxonomy (classification) of computers, one of which was SIMD. Unfortunately, the thread of history is lost on this, but we have not gathered here for this.

Thus, in the 70s of the last century, the first processors appeared, which allowed counting several similar operations on numbers at a time. Later it was dragged to almost all in the form of an extended set of instructions.

Graphically, the classic architecture is as follows:

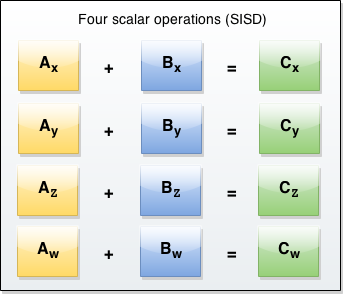
We need to add 4 pairs of numbers, so we have to call the add instruction 4 times in the processor.

The vector operation looks like this:

When we need to add 4 pairs of numbers, we simply call one instruction, which adds them in one measure.

A small remark about the "vector operation" and SIMD-operation. The fact is that SIMD is a more general concept, implying that at one and the same moment of time performing one or several identical operations on different data. In CUDA, at each time point, the threads perform the same operation on different data, but these operations are performed as many threads are available in the video card. Vector arithmetic implies that exactly one operation is performed, and, in fact, it is simply performed on two extended data, which are several of themselves in orderly numbers in one cell. Thus, vector operations are included as a subset in SIMD operations, but ES2017 speaks about vector arithmetic, I don’t know why they decided to generalize this way, then we will consider these two concepts to be the same in this article.

So, it turns out, can we increase the performance of our js applications 4 times? (Extended) Nuuu not really. But first, take a look at how this is done on C (gcc)

 void main() { int a[4] = { 1, 3, 5, 7 }; int b = 3; int c[4]; c[0] = a[0] + b; c[1] = a[1] + b; c[2] = a[2] + b; c[3] = a[3] + b; } 

 #include <xmmintrin.h> extern void printv(__m128 m); int main() { __m128 m = _mm_set_ps(-4, -3, -2, -1); __m128 one = _mm_set1_ps(1.0f); printv(_mm_add_ps(m, one)); // Multiply by one (nop) return 0; } 

 main: .LFB0: .cfi_startproc pushq %rbp .cfi_def_cfa_offset 16 .cfi_offset 6, -16 movq %rsp, %rbp .cfi_def_cfa_register 6 subq $64, %rsp movq %fs:40, %rax movq %rax, -8(%rbp) xorl %eax, %eax movl $1, -48(%rbp) movl $3, -44(%rbp) movl $5, -40(%rbp) movl $7, -36(%rbp) movl $3, -52(%rbp) movl -48(%rbp), %edx movl -52(%rbp), %eax addl %edx, %eax movl %eax, -32(%rbp) movl -44(%rbp), %edx movl -52(%rbp), %eax addl %edx, %eax movl %eax, -28(%rbp) movl -40(%rbp), %edx movl -52(%rbp), %eax addl %edx, %eax movl %eax, -24(%rbp) movl -36(%rbp), %edx movl -52(%rbp), %eax addl %edx, %eax movl %eax, -20(%rbp) nop movq -8(%rbp), %rax xorq %fs:40, %rax je .L2 call __stack_chk_fail 

  movss xmm0, DWORD PTR __real@c0800000 movss xmm2, DWORD PTR __real@c0400000 movss xmm3, DWORD PTR __real@c0000000 movss xmm1, DWORD PTR __real@bf800000 unpcklps xmm3, xmm0 xorps xmm0, xmm0 unpcklps xmm1, xmm2 unpcklps xmm1, xmm3 movaps XMMWORD PTR tv129[esp+32], xmm0 movaps XMMWORD PTR _m$[esp+32], xmm1 addps xmm0, xmm1 

 module adds( input wire[0:31] a, input wire[0:31] b, input wire[0] size, // 8 bit or 16 bit output reg[0:31] c, input wire clk ); always @ (posedge clk) begin case (size) 1'b0: begin c[0:7] <= a[0:7] + b[0:7]; c[8:15] <= a[8:15] + b[8:15]; c[16:23] <= a[16:23] + b[16:23]; c[24:31] <= a[24:31] + b[24:31]; end 1'b1: begin c[0:15] <= a[0:15] + b[0:15]; c[16:31] <= a[16:31] + b[16:31]; end end endmodule 

Practice

So vector operations will soon appear in js. How soon? At the moment, firefox nightly, edge with the "experimental features" flag and the chrome with the flag at startup - --js-flags="--harmony-simd" , i.e. at least in some form, but all browsers. In addition, there is a polyfill , so you can use it right now.

A small example of how to use SIMD in js code:

 const someValue = SIMD.Float32x4(1,0,0,0); const otherValue = SIMD.Float32x4(0,1,0,0); const summ = SIMD.Float32x4.add(someValue, otherValue); 

For a complete list of available functions, see MDN . I want to note that SIMD.Float32x4 is not a designer and the entry is new SIMD.Float32x4(0, 0, 0, 0); is not valid.

I will not describe all the possibilities for using them, there are not very many of them, in general - arithmetic and loading with data upload, some more examples are all on the same MDN , I will go straight to examples.

The designations I have introduced for simplicity of examples are:

 const sload = SIMD.Float32x4.load; const sadd = SIMD.Float32x4.add; const smul = SIMD.Float32x4.mul; const ssqrt = SIMD.Float32x4.sqrt; const sstore = SIMD.Float32x4.store; 

Convolution

A convolution in mathematics refers to the conversion from one data set to another. For programmers, convolution is traversing the entire array and performing a mathematical transformation on each of its elements, for example, multiplying by another number, adding to another array, or using the Sobel operator for the image (it will also be slightly lower).

Scalar option:

Vector:

Here and below: on the vertical axis data, on the horizontal - time. Orange block - the data on which the operation occurs.

In the code, this is an example from above explicitly, on js like this (part of the algorithm for calculating the variance):

 const arr = new Float32Array(someBuffer); for (let i = 0; i < arr.length; i += 4) { //  ,     4,    ! sstore(arr, i, smul( sadd( sload(arr, i), expected // .  ), sadd( sload(arr, i), expected // .  ) )); } 

The sum of the elements of the array

If I am not mistaken, this example is the first in the book on CUDA, and indeed it is the most typical example for SIMD (and, in this case, it is more suitable for computing on a video card, as long as it allows you to go to logarithmic complexity than to vector operations).

I'll tell you the multi-threading algorithm, which is not difficult to adapt to the vector: first, every even (including zero) is summed with the odd, following it. Then the zero (in which the sum a [0] + a [1] now lies) is added to the second even (a [2], which is equal to a [2] + a [3]) and so on. In the next step, 0, 4, 8, ..., then 0, 8, 16, and so on, are combined in powers of two, until the array is finished.

In the case of vector operations, the first 4 values ​​can be summed with the second 4 values, otherwise everything is the same, i.e.

a [0-3] = a [0-3] + a [4-7];

a [8-11] = a [8-11] + a [12-15];

Graphically:

Scalar option

Vector:

Speed ​​increase is expected to be quite large. My js option:

  const length = a.length; let i = 0; let k = 4; while (k < size) { for (i = 0; i < size; i += k * 2) { SIMD.Float32x4.store(a, i, SIMD.Float32x4.add( SIMD.Float32x4.load(a, i), SIMD.Float32x4.load(a, i + k) )); } k = k << 1; } 

This example has a limitation: the size of the array must be at the same time a power of two and a multiple of 4. In principle, this is not so difficult to correct, but we will leave it for homework.

4x4 matrix multiplication

It makes sense to assume that matrix operations for square matrices of size 4 (and with them vectors of the same dimensionality. Mathematical vectors, and not calculating ones) SIMD will give a noticeable increase. What is multiplication and what the classic version looks like, as well as graphically - I will not show it (graphically looks unattractive, the classic version is using the mathematical definition of matrix multiplication in the forehead, you can look at it on Wikipedia), I’ve got the vector code on js:

 let j = 0; let row1, row2, row3, row4; let brod1, brod2, brod3, brod4, row; for (let i = 0; i < 10000; i++) { c = new Float32Array(32); row1 = SIMD.Float32x4.load(a, 0); row2 = SIMD.Float32x4.load(a, 4); row3 = SIMD.Float32x4.load(a, 8); row4 = SIMD.Float32x4.load(a, 12); for (j = 0; j < 4; j++) { d = b[4 * j + 0]; brod1 = SIMD.Float32x4(d, d, d, d); //      _mm_set1_ps d = b[4 * j + 1]; brod2 = SIMD.Float32x4(d, d, d, d); //      _mm_set1_ps d = b[4 * j + 2]; brod3 = SIMD.Float32x4(d, d, d, d); //      _mm_set1_ps d = b[4 * j + 3]; brod4 = SIMD.Float32x4(d, d, d, d); //      _mm_set1_ps row = SIMD.Float32x4.add( SIMD.Float32x4.add( SIMD.Float32x4.mul(brod1, row1), SIMD.Float32x4.mul(brod2, row2) ), SIMD.Float32x4.add( SIMD.Float32x4.mul(brod3, row4), SIMD.Float32x4.mul(brod3, row4) ) ); SIMD.Float32x4.store(c, j * 4, row); } } 

It's hard. I note that after viewing the code into which the c-shny version is compiled, I was not very upset by the lack of _mm_set1_ps, as long as it was compiled inside into 4 separate download commands, so the loss is not great.

Sobel operator

Wikipedia . It is an example of one of the typical tasks that should fit well on SIMD, as long as it is inside a convolution above an image. Pictures, code and algorithm will not, however, I note that in the test I am somewhat cheated. The fact is that the Sobel operator is much more optimized and stronger when using SIMD, but first you need to convert the data to another type, and matan is not easy there. However, even a simple application gave an advantage. As for the honest conversion - even though jpeg is a discrete-cosine transformation, inside it is not so far gone from convolution by the Sobel operator, namely due to SSE (and older) processor extensions, we can watch high-quality video on the processor (and impose much more complex effects using a video card), so this algorithm is the direct assignment of SIMD instructions in the processor, including js.

Is the future here? Performance

Hands test can be run here . Remember to make sure your browser supports SIMD. The source code , do not forget about the fork button, if you have ideas how to improve and optimize.

He took the tests seriously: each test is grouped into 4 starts, one of which is “idle”, designed for warming up the cache and so that the browser can compile what it considers necessary into a binary code. Three are taken into account when calculating. Then each of these groups is run n times, the order is chosen randomly, then the expectation and variance (the black bar on each of the graphs) is considered.

I ran 500 times in each of my groups, which made it possible to eliminate such factors as garbage collection, switching flow, Kaspersky thinking and other windows 10 updates, and reflects numbers close to reality. Unfortunately, it’s impossible to get more accurate conclusions on js for the reason that we can’t force the system’s task scheduler to switch tasks and other things, and to get the number of ticks allocated exclusively for js, there are also no tools (there is a profiler, but he is too hellish from that. Recheck in it - there is a link to the tests at the top, you can inspect it).

Results on my computer (core i5 6400m, firefox nightly 51.0a):

findings

As can be seen from the improvised comparison of performance, with at least a little more or less competent use of technology, it gives an advantage of 20-40%. In specific tasks, you can squeeze even more productivity, as a result, the technology is worth starting to think about its use. Unfortunately, vector programming is quite complicated, there are few specialists in it, especially in the js world, so everyone and everyone will not rush. However, if your project involves complex calculations, a sensitive speed increase will not be superfluous and can save a lot of resources and time for solving other problems.

Now polyfill is available and there is no reason to think that the API for working with SIMD instructions in js will change, while the standard is completed by 90%, and the remaining 10%, secretly, are reflections on how to redefine operators like "+" and "* ". In js, there are no operator overloads and I see no reason to drag them here, so it will most likely be directly included in the standard, which, after being accepted in the nearest release, will be available in firefox and edge. Google in Chrome is not in a hurry with it for some reason, so if you now (at the time of writing this article in August 2016) start your new application on JS, which will have a lot of calculations, you should immediately have this library in view of and ( ), , , , .

, . , x86, , ( a + b * c, ). , - 66AK2x TI ( ) javascript, - . ( Akon32 ,

SIMD-? What for? JS , . , 4- . 3, 5, 8 ? , .
, ( ) JIT ( ), OpenCL/CUDA- API.

: , , , MPi ( OpenMP). , , :

 function summ(a, b, N) { const c = Float32Array(N); let i; /// #pragma omp parallel for shared(a, b, c) private(i) for (i = 0; i < N; i++) c[i] = a[i] + b[i]; } } 

, OpenMP . , 128- , . JIT? , .

PS javascript. , , js , , , , . js .