Using trigrams for correcting recognition results

Natural languages ​​can be characterized by the frequency distribution of the occurrence of their elements, such as words, single letters, or sequences of letters ( N- programs). Formally, an N -gram is a string of N characters belonging to a certain alphabet consisting of a finite number of characters. On the theoretical and applied issues of using the N- grams for automatic text correction can be found in [2].

In this article, we will consider only the alphabet consisting of letters of the Russian language, then we will talk about the possibilities of using trigrams (sequences of three characters) for post-processing (correction to reduce errors) recognition results of Russian-language documents. The recognition mechanism was convolutional neural networks.

1. Description of the trigram model

A trigram model consists of a set (dictionary) of triples of characters { g _{i 1} , g _{i 2} , g _{i 3} } and the weight w _i assigned to them. Trigrams are ordered by weight, more weight means a higher frequency of occurrence of a trigram in a natural language, more precisely in a certain body of texts in a natural language.

In the ideal case, by the weight of the trigram we mean the probability of its occurrence in natural language. Of course, in various samples of natural language texts, we can receive differing trigram weights. As an example, we can consider the texts of classical literature and tables containing the abbreviations of products, it is obvious that for these cases the occurrence of trigrams will vary greatly. At the same time, extracting trigrams from the corpus of homogeneous words makes it possible to obtain stable estimates of trigram weights.

We will tell about the extraction of trigrams from large sets of surnames, names and patronymic names of citizens of the Russian Federation and about the use of the found trigrams for correcting the recognition results of the “Last Name”, “First Name” and “Patronymic” fields in the passport of a citizen of the Russian Federation. Earlier we talked about our software solutions for passport recognition [3, 4], in which the results of this article can be applied.

We had three corpus words at our disposal: dictionaries of surnames, names and patronymic names of citizens of the Russian Federation. Trigrams were extracted from each of the bodies. For each word { c ₁ , c ₂ , ..., c _n } in which c _{i is the} symbol of the Russian language (upper and lower case letters were not distinguished), two dummy characters c _F were added to the beginning and end of the word: { c _F , c _F , c ₁ , c ₂ , ..., c _n ,
c _F , c _F }. This was done so that each of the c _i characters could be matched with trigrams < c _{i -2} , c _{i -1} , c _i > and < c _i , c _{i +1} , c _{i + 2} >, for example, c ₁ You can match the trigram < c _F , c _F , c ₁ >. Next, we will consider words with c _F added to the alphabet. For each triple of characters < g ₁ , g ₂ , g ₃ > we calculated the number of copies of this triple in all words of the corpus, normalized it to the number of possible trigrams and took the normalized value as the weight (the sum of the normalized weights θ ( g ₁ , g ₂ , g ₃ ) is equal to one).

The large body of names used (more than 1,500,000 names in random order, of which there are about 183,000 different names), collected earlier by us from open sources, allowed us to construct a trigram dictionary with weights that depend little on the size of the sample of words. For example, consider the trigrams that are often found in last names.

{O, B, A}, {K, O, B}, {H, O, B}, {I, H, A}, {E, B, A},

weights of which we calculate on samples of different sizes, all samples are taken from the corpus of last names. Figure 1 shows the graphs of the weights of these trigrams versus the sample size, which characterize the stability of determining the weights of these trigrams with a sample size exceeding 50,000 words.

We draw attention to the fact that the most common trigram for the corpus of last names are {A, c _{F ,}
c _F } and {B, A, c _F } with weights of 0.044 and 0.033, respectively.

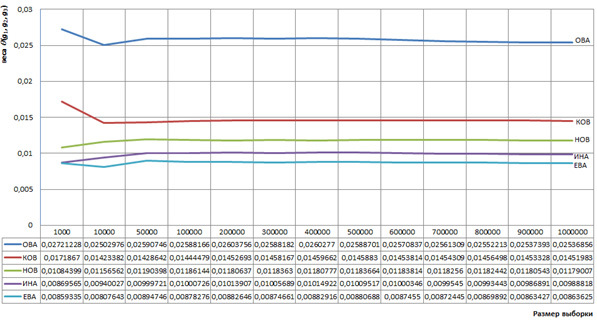
Figure 1. Graphs of examples of trigrams weights depending on sample size

Similarly, trigram dictionaries for names and patronymic names were constructed; in them, when using samples of words of a large amount of weight, frequently occurring trigrams are also calculated stably.

2. Description of recognition results

The results of character recognition are represented by alternatives ( c _j , p _j ):

( c ₁ , p ₁ ), ( c ₂ , p ₂ ), ..., ( c _n , p _q ),

where c _j is the character code, and p _j is the reliability rating of character recognition (hereinafter, recognition scores). If p _j = 1, then the symbol c _{j is} recognized with the greatest reliability, and if p _j = 0, then with the least reliability. In this case, c _j belongs to the recognition alphabet consisting of q characters. All recognition scores have normalization:

0≤ p _j ≤1

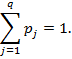
Then the results of recognition of a word consisting of n characters (familiarity) are as follows:

( c ¹ ₁ , p ¹ ₁ ), ( c ¹ ₂ , p ¹ ₂ ), ..., ( c ¹ _n , p ¹ _n )

( c ² ₁ , p ² ₁ ), ( c ² ₂ , p ² ₂ ), ..., ( c ² _n , p ² _n )

...

( c ^q ₁ , p ^q ₁ ), ( c ^q ₂ , p ^q ₂ ), ..., ( c ^q _n , p ^q _n ).

The character recognition mechanism may be wrong. The recognized word is considered recognized with errors or without errors depending on the difference or coincidence of the well-known “ideal” word c ^* ₁ c ^* ₂ ... c ^* _n , which was previously specified by the person, with the sequence of characters c ¹ ₁ c ¹ ₂ ... c ¹ _n extracted from the first alternatives {( c ¹ ₁ , p ¹ ₁ ), ( c ¹ ₂ , p ¹ ₂ ), ... ( c ¹ _n , p ¹ _n )}. We define for the set of recognized words the recognition accuracy as the fraction of words recognized without errors.

Below is an example of the results of the recognition of the names of "EPIFANOV":

In the example, one familiarity (the letter “H”) is recognized with an error, so the entire word will be considered as recognized as a mistake.

For the experiments described below, two test data sets were used: T ₁ (2,722 words, consisting of 22,103 characters with low quality of digitization and, respectively, with low recognition accuracy) and T ₂ (2,354 words, consisting of 19,230 characters with average quality of digitization and more reliable recognition). Set T1 consisted of 896 examples of surnames, 915 examples of names, 911 examples of patronymic names, and set T ₂ of 776 examples of surnames, 794 examples of names and 784 examples of patronymic names, respectively.

It was written above that the recognition scores p ^k _{j were} interpreted as probabilities. Let us look at the T ₁ and T ₂ sets, how the recognition scores p ^k _j correlate with the number of errors that occurred. To do this, we construct a histogram of the number of errors of our recognition mechanism that happened to characters with estimates of p ^k _j from a certain range of the interval [0,1]. For clarity, we divide the interval [0,1] into 32 intervals [0, 1/32), [1/32, 2/32), ... [31/32, 1] and for the set of recognized characters with estimates of p ^k _j from the interval [ d / 32, ( d +1) / 32) calculate the number of mistakenly recognized characters. This histogram is shown in Figure 2, the type of histogram argues in favor of interpreting the recognition scores p ^k _j as probabilities, since there are many errors for small values ​​of estimates, and few errors for large values ​​(close to 1). More precisely, for large values ​​of recognition scores (more than 26/32), there are no errors at all. We did not do more accurate studies of the correlation of the recognition scores and the probabilities (frequencies) of the occurrence of errors due to the limited volume of the T ₁ and T ₂ sets.

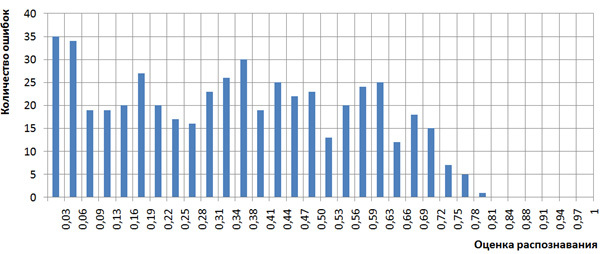
Figure 2. Histogram of the number of recognition errors depending on the recognition scores

3. Algorithms for the correction of recognition results using trigrams

We describe a simple algorithm 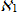for the correction of recognition results.

For all characters with ^k _i for 1≤ i ≤ n , 1≤ k ≤ q (i.e., for all characters that are not fictitious), consider the two preceding characters with ^k _{i -2} , with ^k _{i -1} , which are considered already selected (fixed) and using ready-made trigrams < with ^k _{i -2} , with ^k _{i -1} , with ^k _i >, containing the symbol with ^k _i , we calculate the new estimate:

sort alternatives by new values ^k _i and fix the character to correct the next character with ^k _{i + 1} . That is, first we recalculate the values ​​of the estimates for the first character of the word, taking into account the two dummy characters that we consider to be chosen, and fix the first character. After recalculating the ratings of the next character, we move on to the next character and so on.

The formulas used assumptions that θ ( with ^k _{i -2} , with ^k _{i -1} , with ^k _i ) and p ^k _i are probabilities. We expected from the algorithm 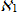Correction of some recognition errors due to the fact that incorrect and rarely encountered triples of recognized characters with ^k _{i -2} , with ^k _{i -1} , with ^k _i will be replaced with those that occur more frequently.

Consider the results of the algorithm 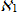On sets T ₁ and T ₂ , summarized in Tables 1 and 2. These and subsequent similar tables contain data on words that were recognized with errors, and on unmistakably recognized words and used the following characteristics:

n ₁ is the number of words without errors both in the initial recognition and when using the trigram mechanism;

n ₂ - the number of words with errors in the original recognition, not corrected by trigrams;

n ₃ - the number of words with errors in the original recognition, corrected trigram

n ₄ - the number of words without errors in the original recognition, in which the use of trigrams introduced errors.

Table 1. The results of the algorithm 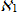on test set T ₁

Table 2. The results of the algorithm 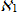on test set T ₂

From the tables it follows that the adjustment algorithm 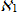It gives interesting results, because trigrams correct more errors than they introduce. At the same time, the question arises, how can we explain the dependence of the character of a word on the two previous characters? This question remains unanswered; this dependence cannot be justified. However, the adopted dependence contributed to the creation of a very simple algorithm.

We will not expose the described algorithm 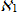Further criticism, we only note that you can come up with many similar simple algorithms, for example, with the dependence of a symbol on two consecutive or on two adjacent symbols, and these algorithms will also give acceptable results.

We set a goal to develop an algorithm without involving the conditions of dependence of characters on neighboring symbols, assuming that such an algorithm, being more rigorous, would work better than 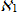. Designed algorithm adjusting recognition results using trigrams is based on calculations of marginal distributions and Bayesian networks.

For a word of n characters, we associate a random variable with each familiarity 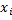with values ​​in finite state space 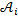and suppose that 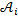is the recognition alphabet A , that is, the set of letters of the Russian language, in which uppercase and lowercase letters do not differ. Denote by N = {1, ..., n } the set of indices. Name the piece 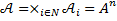space of finite vector configurations 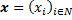. Next, build the graph 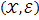according to the following rule. Lots of is a set of vertices of the graph. We assume that with each triple of vertices < x _j , x _{j +1} , x _{j +2} > there is associated a normalized weighting function of trigrams 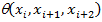. Connect the edges of the top of the triple with each other, the set of obtained edges forms a set .

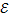We write the formula for the joint distribution of probabilities

/

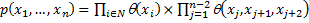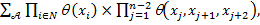
Where 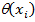- the function of recognition scores for the i- th familiarity, 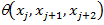Is the normalized function of trigram weights.

To recalculate the estimates, it is enough to calculate marginal distributions.

.

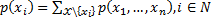We implemented the calculation of marginal distributions using the HUGIN algorithm [5, 6]. Without disclosing implementation details, we point out that this algorithm is significantly more complex than the algorithm .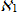

The results of the algorithm on the same sets of T ₁ and T ₂ are summarized in tables 3 and 4, while the results of the algorithm are added to the tables 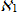for comparison. Also in Tables 3 and 4, the accuracy characteristics of the algorithms are added.

Table 3. The results of the algorithms 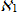and on test set T ₁

Table 4. The results of the algorithms 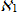and on test set T ₂

4. Discussion of the results of the algorithms

From Tables 3 and 4, it follows that on the T ₁ and T ₂ sets both algorithms significantly improve the initial recognition results, with low digitization quality, the recognition accuracy can be increased by more than 6%. In all cases considered, the algorithm gives better results than algorithm .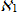

The disadvantage of the algorithm is the use of an unsubstantiated hypothesis about the dependence of a symbol on the two previous symbols.

The disadvantage of the algorithm is significantly lower speed compared to the speed of the algorithm - more than 100 times. However, it should be noted that the algorithm being very simple, it processes one word in about 0.001 seconds.

In some cases, the use of trigrams leads to a deterioration of the correct recognition results. Basically, such cases are due to the following two reasons:

• the original recognition did not give a very confident result with low marks for the first alternative, and trigrams derived from other alternatives have more weight (for example, in the word “DINAR” familiarity with the “D” symbol has a low score of 0.57, and this leads to to the “L” symbol due to the fact that the weight of the “DIN” trigram is approximately equal to 0.0001, and the weight of the “LIN” trigram is approximately equal to 0.0034),
• There are no trigrams in the trigram dictionary, which are necessary for confirming triples of characters in rare names, surnames or patronymic names (for example, the trigram dictionary does not contain the “” trigram, causing the word “AZRWARD” to be replaced with “AZRAARD”).

The distribution of the number of recognition errors depending on the recognition scores after the application of trigrams also looks “improved”. Figure 3 shows the histogram calculated after applying trigrams using the algorithm , in comparison with the original histogram. It is seen that in almost all the intervals of the estimates the number of errors is reduced.

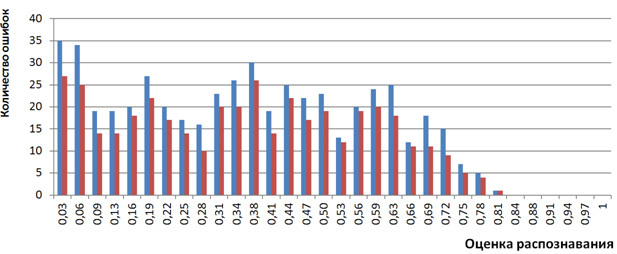
Figure 3. Histogram of the number of recognition errors depending on the recognition scores before (blue) and after (red) the application of trigrams

Conclusion

We showed a method for correcting recognized documents using the trigram mechanism using the example of passport fields (full name) of a citizen of the Russian Federation. Two algorithms of such a correction and the main problems of their work were described. It is essential to have reasonable reliability estimates, formed by the recognition mechanism, and a representative sample of words for constructing a trigram vocabulary.

The described algorithms are used to correct recognition results in running software products Smart Engines.

List of useful sources

1. Shchutsky Yu. K. Chinese Classical "Book of Changes". - 2nd ed. corrected and add. / Ed. A.I. Kobzev. - M .: Science, 1993.
2. Kukich, K. Techniques for Automatically Correcting Words in Text. ACM computing survey, Computational Linguistic, V. 24, No. 4, 377-439. 1992
3. "Passport scanner with your own hands" ( https://habrahabr.ru/company/smartengines/blog/278257/ )
4. "Recognition of the Passport of the Russian Federation on a mobile phone" ( https://habrahabr.ru/company/smartengines/blog/252703/ )
5. R. Cowell, P. Dawid, S. Lauritzen, D. Spiegelhalter. Probabilistic Networks and Expert Systems. Springer, 1999.
6. Michael I. Jordan. An introduction to probabilistic graphical models. Manuscript used for Class Notes of CS281A at UC Berkeley, Fall 2002.