The logic of consciousness. Part 1. Waves in the cellular automaton

Let's start the conversation about the brain with a somewhat abstract topic. Let's talk about cellular automata. A cellular automaton is a discrete model that describes a regular grid of cells, the possible states of the cells, and the rules for changing these states. Each of the cells can take a finite set of states, for example, 0 and 1. For each of the cells, a neighborhood is defined that defines its neighbors. The state of the neighbors and the own state of the cell determine its next state.
The most famous cellular automaton is the game "Life . " The field in the game "Life" consists of cells. Each cell has eight neighbors. Sets the initial combination. Then begins the change of generations. If a busy cell has two or three busy (living) neighbors, then the cell continues to live. If there are less than 2 neighbors or more than 3, then the cell dies. When an empty cell has exactly 3 neighbors, life begins in it. By setting an arbitrary initial combination, one can observe its evolution.



Potentially, the cells, when choosing the next state, can take into account not only the state of the neighborhood and the transition rules, but also experience as to what they had previously encountered. Then it is customary to talk about cellular automata with memory.

Imagine the following cellular automaton. Arrange the elements (cell automaton) on a regular grid. For each element, we define a neighborhood with radius R, which will be the tracking area of ​​this element.
')

The plane of the cellular automaton. The tracking area of ​​the selected item is circled in red.

Suppose that somehow a compact activity pattern has appeared on the plane of the automaton (figure below). Compactness means that all active elements fall into a region of radius R.


Initial activity pattern. Only active items are shown. Elements are depicted tightly, without a gap. Each point in the picture corresponds to one element.

Now let's calculate how many active elements fell into the field of tracking each of the elements (figure below).


Tracking field for one of the elements and active elements in this field

Let us set some small probability p (in the example it is 3%). For each element in a quiet state, in which the number of active elements in the tracking field exceeds a certain threshold, we perform the following procedure. Let's make the element randomly with a probability p go to the active state. Accordingly, with probability 1 - p the element will remain in an inactive state. Let us memorize personally for this element his choice and the pattern of activity in his field of tracking.

As a result, an environment is formed around the initial activity pattern of active elements that form a randomly generated pattern (figure below). For reasons that will soon become clear, let's call such activity wave.


The first step is modeling. Wave activity (gray) on the background of the initial activity (red)

Let's move to a new tact. In the second cycle of the simulation, elements located along the perimeter of the wave activity zone will “see” the activity that has recently occurred. Repeat the activation procedure for them. The elements that became active in the previous step, we translate into a state of relaxation, that is, turn off their activity and for a certain time block their ability to be excited with respect to the propagated signal.


The second step is modeling. Wave front propagation. The blue elements are in a state of relaxation.

Repeating the steps of the simulation, we get the activity spreading along the machine with a certain unique randomly created pattern.


A series of cycles of the primary distribution of the pattern of wave activity. White dots are active elements forming the wave front. Blue dots - elements that are in a state of relaxation with respect to the propagated signal

If you create another compact activity pattern in the machine, it will also generate the wave front propagating from it. But, importantly, the pattern of the new wave will be unique and different from the pattern of the previous wave. Any initial activity pattern will generate a unique, characteristic only for him wave.

Changing the initial pattern, we will receive a new wave every time. In this case, the elements of the machine will remember what patterns have already run through them. We introduce the rule of wave excitation. Each element that has found a high level of activity around it will have to check if the picture of this activity does not look like one of the previously remembered patterns. If the picture turns out to be familiar to him, then he should behave in the same way as during the first passage of such a wave.

The final logic of our machine can be described as follows: if an element sees an unfamiliar signal, then it is randomly determined to trigger it or not. At the same time, he remembers both the wave pattern and the choice made. If the signal is familiar to him, he repeats the choice made at the first acquaintance with this signal. Joint operation of elements generates a wave front diverging from the initial activity pattern. Relaxation provides unidirectional wave propagation from places where activity has already been to the side where it has not yet existed.



For each radiating pattern, the wave will, firstly, have a unique propagation pattern that is different from all other waves, and secondly, this pattern will always be the same for the same triggering pattern. This means that if we introduce a dictionary of concepts and compare each concept with a certain pattern coding it, then we will be able to transmit information about the activity of a concept across the entire surface of the cellular automaton. Since each pattern generates a wave with a unique pattern, then anywhere in the cellular automaton, according to the pattern of the passing wave, one can judge what concept is being propagated by this wave. The figure below shows how the patterns of different waves differ, passing through the same place.


Wave patterns from different initial patterns appearing in the same place of the cellular automaton

If the signal is encoded by a sufficiently small percentage of active elements, then several signals can propagate along the machine simultaneously, preserving their individuality and not interfering with each other. With the simultaneous propagation of several waves, the fronts of these waves can pass through each other without changing their pattern.


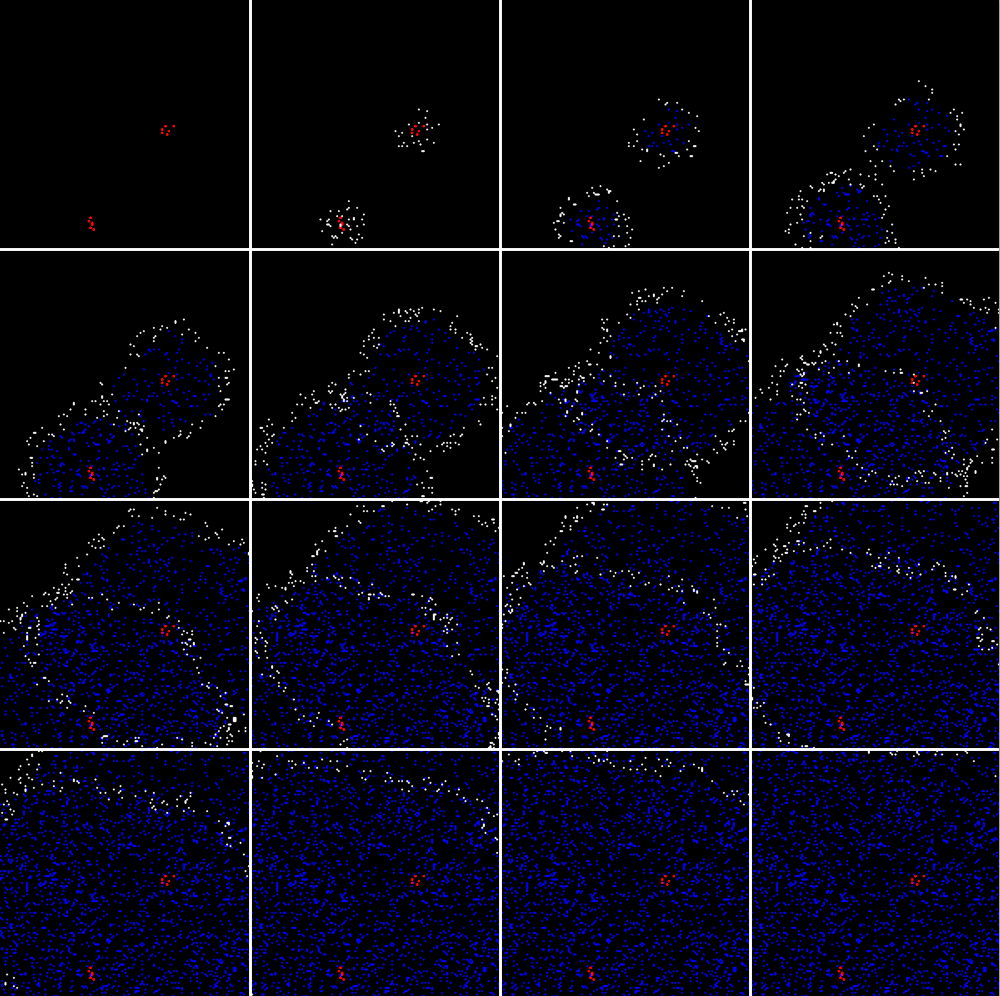
Simulation of the mutual passage of waves from two sources. Before the automaton was trained for each of the waves separately

At the same time, several waves may propagate along the machine, corresponding to different signals. However, with an increase in their number, sooner or later there comes a moment when the imposition of several wave patterns leads to the appearance of false positives. False alarms avalanche increase the number of active elements. From a certain moment, a mode of self-excitation arises, the picture of which strongly resembles the picture of an epileptic seizure.

It is worth noting that the signals encoded by such an automaton acquire the property of dualism, which corresponds to the dualism of elementary particles. As well as particles that simultaneously exhibit both particle and wave properties, the information signal in the described model is both a pattern that triggers a wave and a wave, which in each phase of its path turns into a pattern, which, in turn, radiates the continuation of the wave. The Huygens-Fresnel principle is applicable to the propagation of an information wave, where each point where the wave front has reached can be considered as an independent source of spherical wave radiation.

The described algorithm for the formation of waves has a significant drawback. When an element sees a wave for the first time, it makes a choice to participate in it or not, and then remembers the choice made along with the wave pattern visible to it. This allows the next time to get the repeatability of the wave pattern. But at the same time, an element can recognize a wave only when it comes from the same side as at the moment of memorization. It is easy to modify the algorithm to get rid of this drawback. It is enough to postpone the moment of memorizing a new wave. Instead of memorizing the pattern at the moment when the new wave approached the element, you can let the wave propagate a bit further and remember the pattern that turned out around the element. The procedure for the subsequent recognition of the wave is also changing. A wave is considered recognized if a repetition of a part of the memorized pattern has occurred near the element.

As a result, the elements of the automaton become invariant to the direction of wave propagation. That is, the same wave pattern is reproduced in the same way, regardless of where the front of this wave came from.

Such a revision of the machine adds to it a very important property. Take an arbitrary familiar automaton concept. This concept will correspond to a wave with a unique pattern. If a fragment of such a pattern is reproduced anywhere in the plane of the automaton, then a wave will propagate from this place, reproducing the unique pattern of the original wave all along its path. For example, if on the machine (picture below) in the encircled area (1) create a certain pattern, then, having reached the place (2), the wave front will create some pattern unique for this wave.


The original pattern triggers a wave from the region (1) and, reaching the region (2), creates a unique pattern there.

If now in the area (2) to reproduce the pattern that was there when the wave front passed, then a wave will emit from this place, repeating the original pattern (figure below). Reaching the area (1), it will create a pattern identical to the one that once launched the original wave.


The new wave starts from the area (2) with the pattern that was part of the original wave. The wave front, having reached the area (1), creates there a pattern similar to the original

Thus, the complete connectedness of the entire space of the automaton is obtained. That is, potentially any of his place can start an information wave and at the same time all parts of the machine where the corresponding wave reaches will get access to this information.

A program simulating such a cellular automaton is available here . The described cellular automaton is somewhat similar to a traveling wave in a stadium.



In the stands, everyone gets up when the wave front reaches them and sits down after a second. The result is a solid wave. Now imagine that you should only get up if certain neighbors have already stood next to each other (for example, specific three of the twenty who are sitting next to each other). And suppose you have a list of combinations to which you must respond. Suppose that everyone in the stadium has its own list. Then it will no longer be a continuous wave, but a pattern made up of those who stood up, recognizing a combination from their list. If you look at such a structure from a long distance, then we will see just a traveling wave. But if you look at a particular place of the wave front, then we will make out a pattern made up of people who have risen.

On such a podium, you can send simple messages. For example, wave patterns can match letters. If you start a pattern of a letter in one end of the podium, then in any other place of the podium, when a wave reaches it, you can tell by the pattern of this wave which letter is transmitted.

So far this is not the brain, but only the cellular automaton. In the next section, it will be shown how this automaton can be related to the real brain.

PS I strongly advise to read a little more about cellular automata and how they can be connected with the structure of the universe and especially pay attention to the personality of Konrad Tsuze .

Alexey Redozubov

The logic of consciousness. Introduction
The logic of consciousness. Part 1. Waves in the cellular automaton
The logic of consciousness. Part 2. Dendritic waves
The logic of consciousness. Part 3. Holographic memory in a cellular automaton
The logic of consciousness. Part 4. The secret of brain memory
The logic of consciousness. Part 5. The semantic approach to the analysis of information
The logic of consciousness. Part 6. The cerebral cortex as a space for calculating meanings.
The logic of consciousness. Part 7. Self-organization of the context space
The logic of consciousness. Explanation "on the fingers"
The logic of consciousness. Part 8. Spatial maps of the cerebral cortex
The logic of consciousness. Part 9. Artificial neural networks and minicolumns of the real cortex.
The logic of consciousness. Part 10. The task of generalization
The logic of consciousness. Part 11. Natural coding of visual and sound information
The logic of consciousness. Part 12. The search for patterns. Combinatorial space