Faster fast or deep optimization Median filtering for Nvidia GPUs
Introduction
In the previous post, I tried to describe how easy it is to take advantage of the GPU for image processing. The fate was such that I turned up the opportunity to try to improve the median filtering for the GPU. In this post I will try to tell you how you can get even more performance from the GPU in image processing, in particular, using the example of median filtering. We will compare the GTX 780 ti GPU with optimized code running on a modern Intel Core i7 Skylake 4.0 GHz processor with a set of AVX2 vector registers. The achieved filtration rate by 3x3 square at 51 GPixels / sec for the GTX 780Ti GPU and specific filtration rate by 3x3 square at 10.2 GPixels / sec per 1 TFlops for single accuracy at this time are the highest among all known in the world .
For clarity of what is happening, it is strongly recommended to read the previous post , since this post will be tips, recommendations and approaches for improving the already written version. To remind you what we are doing:
- For each point of the original image, a certain neighborhood is taken (in our case, 3x3 / 5x5).
- The points of this neighborhood are sorted by increasing brightness.
- The average point of the sorted neighborhood is written to the final image.
3x3 square median filter
One of the ways to optimize the image processing code on the GPU is to find and select repeated operations and make them only once inside one warp. In some cases, you will need to change the algorithm slightly. Looking at the filtering, you can see that by loading a 3x3 square around one pixel, neighboring threads do the same logical operations and the same load from memory:
__global__ __launch_bounds__(256, 8) void mFilter_33(const int H, const int W, const unsigned char * __restrict in, unsigned char *out) { int idx = threadIdx.x + blockIdx.x * blockDim.x + 1; int idy = threadIdx.y + blockIdx.y * blockDim.y * 4 + 1; unsigned a[9] = { 0, 0, 0, 0, 0, 0, 0, 0, 0 }; if (idx < W - 1) { for (int z3 = 0; z3 < 4; ++z3) { const int shift = 8 * (3 - z3); for (int z2 = 0; z2 < 3; ++z2) for (int z1 = 0; z1 < 3; ++z1) a[3 * z2 + z1] |= in[(idy - 1 + z2) * W + idx - 1 + z1] << shift; // <----- warp // 6 12 // idy += BL_Y; } /* */ } } A little thought, you can improve the sorting, doing the same operation only once. For clarity, I will show what sorting was and what has become, and what is the benefit of this approach.
In the previous post I used Batcher’s already invented incomplete sorting for 9 elements, which allows us to find the median without using conditional operators for the minimum number of operations. Imagine this sorting in the form of iterations, each of which sorts independent elements, but there are dependencies between the iterations. For each iteration selected pairs of items to sort.
Old sorting:
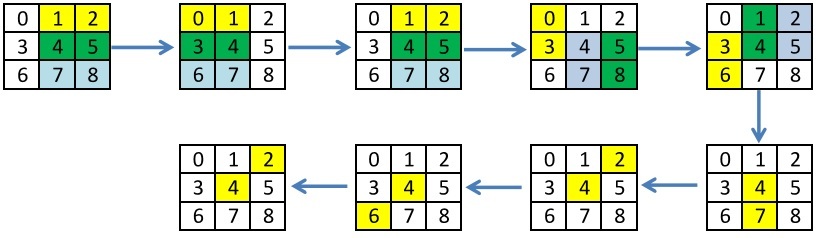
New Sort:

In appearance, both approaches can be said to be the same. But let's look at it from the point of view of optimization by the number of operations and the ability to use the calculated values by other threads. You can load and sort the columns only once, make exchanges between threads and calculate the median. Clearly it will look like this:
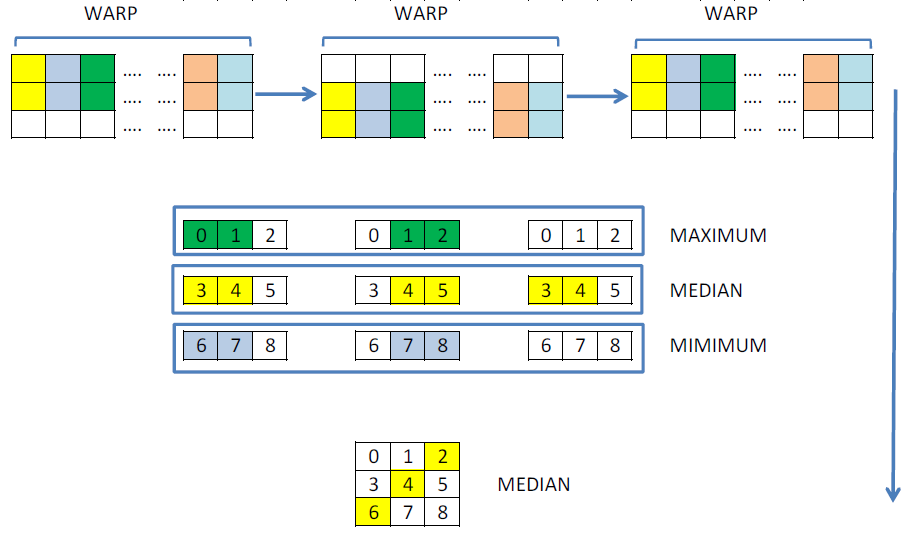
This algorithm corresponds to the following core. For exchanges, I decided not to use shared memory, but new operations __shfl, which allow exchanging values within one warp without synchronization. Thus, it is possible partially not to do repeated calculations.
__global__ BOUNDS(BL_X, 2048 / BL_X) void mFilter_3x3(const int H, const int W, const unsigned char * __restrict in, unsigned char *out) { // int idx = threadIdx.x + blockIdx.x * blockDim.x; // , warp' idx = idx - 2 * (idx / 32); // 4, 4 int idy = threadIdx.y + blockIdx.y * blockDim.y * 4 + 1; unsigned a[9]; unsigned RE[3]; // bool bound = (idxW > 0 && idxW < 31 && idx < W - 1); // RE[0] = in[(idy - 1) * W + idx] | (in[(idy + 0) * W + idx] << 8) | (in[(idy + 1) * W + idx] << 16) | (in[(idy + 2) * W + idx] << 24); RE[1] = in[(idy + 0) * W + idx] | (in[(idy + 1) * W + idx] << 8) | (in[(idy + 2) * W + idx] << 16) | (in[(idy + 3) * W + idx] << 24); RE[2] = in[(idy + 1) * W + idx] | (in[(idy + 2) * W + idx] << 8) | (in[(idy + 3) * W + idx] << 16) | (in[(idy + 4) * W + idx] << 24); Sort(RE[0], RE[1]); Sort(RE[1], RE[2]); Sort(RE[0], RE[1]); // a[0] = __shfl_down(RE[0], 1); a[1] = RE[0]; a[2] = __shfl_up(RE[0], 1); a[3] = __shfl_down(RE[1], 1); a[4] = RE[1]; a[5] = __shfl_up(RE[1], 1); a[6] = __shfl_down(RE[2], 1); a[7] = RE[2]; a[8] = __shfl_up(RE[2], 1); // a[2] = __vmaxu4(a[0], __vmaxu4(a[1], a[2])); // Sort(a[3], a[4]); a[4] = __vmaxu4(__vminu4(a[4], a[5]), a[3]); // a[6] = __vminu4(a[6], __vminu4(a[7], a[8])); // Sort(a[2], a[4]); a[4] = __vmaxu4(__vminu4(a[4], a[6]), a[2]); // , if (idy + 0 < H - 1 && bound) out[(idy) * W + idx] = a[4] & 255; if (idy + 1 < H - 1 && bound) out[(idy + 1) * W + idx] = (a[4] >> 8) & 255; if (idy + 2 < H - 1 && bound) out[(idy + 2) * W + idx] = (a[4] >> 16) & 255; if (idy + 3 < H - 1 && bound) out[(idy + 3) * W + idx] = (a[4] >> 24) & 255; } The second optimization is connected with the fact that each thread can process not 4 points at once, but, for example, 2 sets of 4 points each or N sets of 4 points each. This is necessary in order to maximize the load of the device, since it is not enough for a 3x3 filter of one set of 4 points.
The third optimization that can still be done is to perform the substitution of the width and height of the image. There are several arguments to this:
- Typically, the size of the pictures have fixed values, for example, popular Full HD, Ultra HD, 720p. You can simply have a set of precompiled kernels. This optimization gives about 10-15% of performance.
- Since Cuda Toolkit 7.5, it is possible to perform dynamic compilation, which allows you to perform value substitution at runtime.
Fully optimized code will look like this. Varying the number of points, you can get maximum performance. In my case, the maximum performance was achieved with numP_char = 3, that is, three sets of 4 points or 12 points per thread.
__global__ BOUNDS(BL_X, 2048 / BL_X) void mFilter_3x3(const unsigned char * __restrict in, unsigned char *out) { int idx = threadIdx.x + blockIdx.x * blockDim.x; idx = idx - 2 * (idx / 32); int idxW = threadIdx.x % 32; int idy = threadIdx.y + blockIdx.y * blockDim.y * (4 * numP_char) + 1; unsigned a[numP_char][9]; unsigned RE[numP_char][3]; bool bound = (idxW > 0 && idxW < 31 && idx < W - 1); #pragma unroll for (int z = 0; z < numP_char; ++z) { RE[z][0] = in[(idy - 1 + z * 4) * W + idx] | (in[(idy - 1 + 1 + z * 4) * W + idx] << 8) | (in[(idy - 1 + 2 + z * 4) * W + idx] << 16) | (in[(idy - 1 + 3 + z * 4) * W + idx] << 24); RE[z][1] = in[(idy + z * 4) * W + idx] | (in[(idy + 1 + z * 4) * W + idx] << 8) | (in[(idy + 2 + z * 4) * W + idx] << 16) | (in[(idy + 3 + z * 4) * W + idx] << 24); RE[z][2] = in[(idy + 1 + z * 4) * W + idx] | (in[(idy + 1 + 1 + z * 4) * W + idx] << 8) | (in[(idy + 1 + 2 + z * 4) * W + idx] << 16) | (in[(idy + 1 + 3 + z * 4) * W + idx] << 24); Sort(RE[z][0], RE[z][1]); Sort(RE[z][1], RE[z][2]); Sort(RE[z][0], RE[z][1]); a[z][0] = __shfl_down(RE[z][0], 1); a[z][1] = RE[z][0]; a[z][2] = __shfl_up(RE[z][0], 1); a[z][3] = __shfl_down(RE[z][1], 1); a[z][4] = RE[z][1]; a[z][5] = __shfl_up(RE[z][1], 1); a[z][6] = __shfl_down(RE[z][2], 1); a[z][7] = RE[z][2]; a[z][8] = __shfl_up(RE[z][2], 1); a[z][2] = __vmaxu4(a[z][0], __vmaxu4(a[z][1], a[z][2])); Sort(a[z][3], a[z][4]); a[z][4] = __vmaxu4(__vminu4(a[z][4], a[z][5]), a[z][3]); a[z][6] = __vminu4(a[z][6], __vminu4(a[z][7], a[z][8])); Sort(a[z][2], a[z][4]); a[z][4] = __vmaxu4(__vminu4(a[z][4], a[z][6]), a[z][2]); } #pragma unroll for (int z = 0; z < numP_char; ++z) { if (idy + z * 4 < H - 1 && bound) out[(idy + z * 4) * W + idx] = a[z][4] & 255; if (idy + 1 + z * 4 < H - 1 && bound) out[(idy + 1 + z * 4) * W + idx] = (a[z][4] >> 8) & 255; if (idy + 2 + z * 4 < H - 1 && bound) out[(idy + 2 + z * 4) * W + idx] = (a[z][4] >> 16) & 255; if (idy + 3 + z * 4 < H - 1 && bound) out[(idy + 3 + z * 4) * W + idx] = (a[z][4] >> 24) & 255; } } Median filter 5x5 square
Unfortunately, I did not manage to come up with any other sorting for the 5x5 square. The only thing you can save on is to load and combine 4 points in an unsigned int. I don’t see any point in citing a longer code, since all the transformations can be done by analogy with a 3x3 square.
This article describes some ideas for combining operations for two squares with an overlay of 20 elements. But the forgetful selection sort method proposed by the authors still does more operations than Batcher’s incomplete sorting network for 25 elements, even when combining two adjacent 5x5 squares.
Performance
Finally, I will give some figures that I was able to get throughout the entire optimization process.
| Runtime, ms | Acceleration | |||||
|---|---|---|---|---|---|---|
| Scalar CPU | AVX2 CPU | GPU | Scalar / GPU | AVX2 / GPU | ||
| 3x3 1920x1080 | 22.9 | 0.255 | 0.044 (47.1 GP / s) | 520 | 5.8 | |
| 3x3 4096x2160 | 97.9 | 1.33 | 0.172 (51.4 GP / s) | 569 | 7.73 | |
| 5x5 1920x1080 | 134.3 | 1.47 | 0.260 (7.9 gp / s) | 516 | 5.6 | |
| 5x5 4096x2160 | 569.2 | 6.69 | 1,000 (8.8 gp / s) | 569 | 6.69 | |
Conclusion
In conclusion, I would like to note that among all the found articles and implementations of median filtering for the GPU, the article already mentioned is of interest “Fine-tuned high-speed implementation of a GPU-based median filter”, published in 2013. In this article, the authors proposed a completely different approach to sorting, namely, the forgetful selection method. The essence of this method is that we take roundUp (N / 2) + 1 elements, we pass from left to right and back, thus obtaining the minimum and maximum elements at the edges. Next, we forget these elements, add one of the remaining elements to the end and repeat the process. When there is nothing to add, we will get an array of 3 elements, from which it will be easy to choose the median. One of the advantages of this approach is the reduced number of registers used, compared with the known sorting.
The article states that the authors obtained a result of 1.8 GPixels / sec on the Tesla C2050. The power of this card in single precision is estimated at 1 TFlops. The power involved in testing the 780Ti is estimated at 5 TFlops. Thus, the specific calculation speed per 1 TFlops of the algorithm proposed by me is approximately 5.5 times more for a 3x3 square and 2 times more for a 5x5 square than the one proposed by the authors of the article. This comparison is not entirely correct, but closer to the truth. Also in this article it was mentioned that at that time their implementation was the fastest of all known.
The achieved acceleration compared with the AVX2 version averaged 6 times. If you use new cards based on the Pascal architecture, this acceleration may increase at least 2 times, which will be approximately 100 GPixels / sec.
')
Source: https://habr.com/ru/post/308214/
All Articles