Training with reinforcements for the smallest
This article explores the principle of the “Learning with reinforcement” machine learning method using the example of a physical system. The algorithm for finding the optimal strategy is implemented in Python code using the Q-Learning method.
Reinforcement training is a machine learning method in which a model is trained that has no knowledge of the system, but has the ability to perform some actions in it. Actions take the system to a new state and the model receives some reward from the system. Consider the work of the method on the example shown in the video. In the description of the video is the code for Arduino , which is implemented in Python .
Using the “reinforcement training” method, it is necessary to teach the trolley to move away from the wall to the maximum distance. The award is presented in the form of the value of changing the distance from the wall to the trolley during movement. Measurement of the distance D from the wall is made by a range finder. The movement in this example is possible only at a certain offset of the “drive” consisting of two arrows S1 and S2. Arrows are two servo with guides connected in the form of "knee". Each servo in this example can be rotated by 6 identical angles. The model has the ability to perform 4 actions that represent the control of two servo drives, action 0 and 1 rotate the first servo at a certain angle clockwise and counterclockwise, action 2 and 3 rotate the second servo drive at a certain angle clockwise and counterclockwise. Figure 1 shows the working prototype of the trolley.
')

Fig. 1. Prototype carts for machine learning experiments
In Figure 2, the S2 arrow is highlighted in red, the S1 arrow is highlighted in blue, and 2 servo actuators in black.

Fig. 2. Engine system
The system diagram is shown in Fig. 3. The distance to the wall is marked D, the yellow shows the range finder, the system drive is highlighted in red and black.

Fig. 3. System diagram
The range of possible positions for S1 and S2 is shown in Figure 4:

Fig. 4.a. S1 boom range

Fig. 4.b. S2 boom range
The limiting positions of the drive are shown in Figure 5:
When S1 = S2 = 5, the maximum distance from the ground.
When S1 = S2 = 0, the minimum distance to the ground.
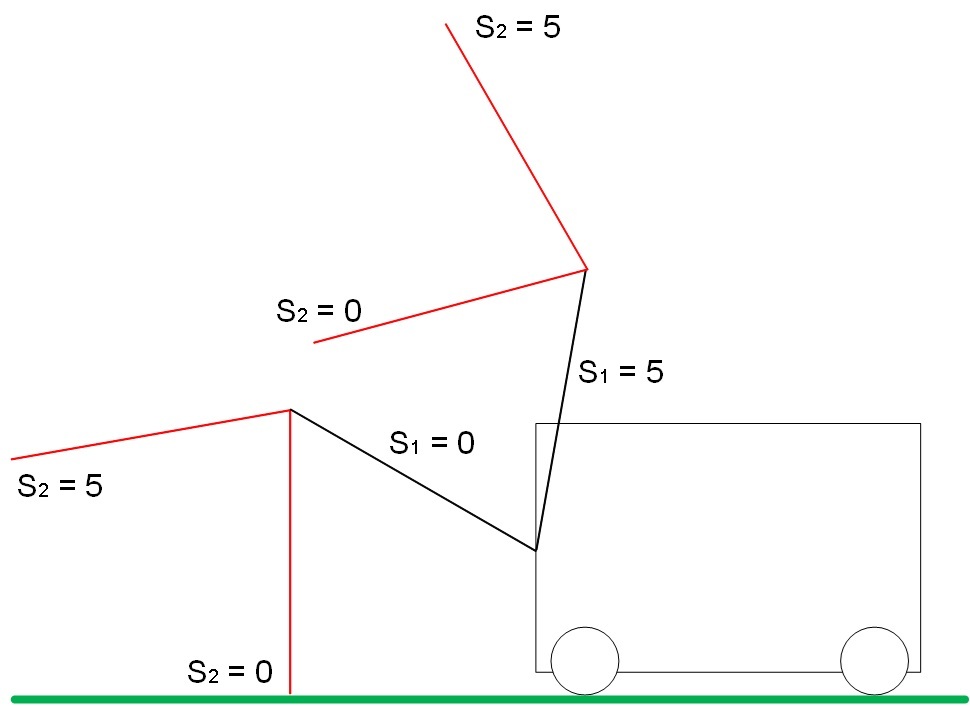
Fig. 5. Border positions of arrows S1 and S2
The "drive" 4 degrees of freedom. The action (action) changes the position of the arrows S1 and S2 in space according to a certain principle. Types of actions are shown in Figure 6.
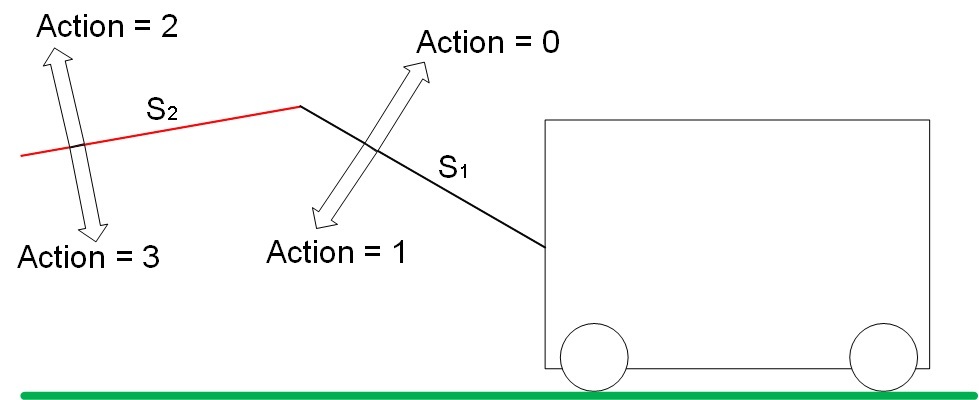
Fig. 6. Types of actions (Action) in the system
Action 0 increases the value of S1. Step 1 reduces the value of S1.
Step 2 increases the value of S2. Step 3 reduces the value of S2.
In our task, the cart is driven only in 2 cases:
In position S1 = 0, S2 = 1, action 3 drives the trolley away from the wall, the system receives a positive reward equal to the change in distance from the wall. In our example, the reward is 1.
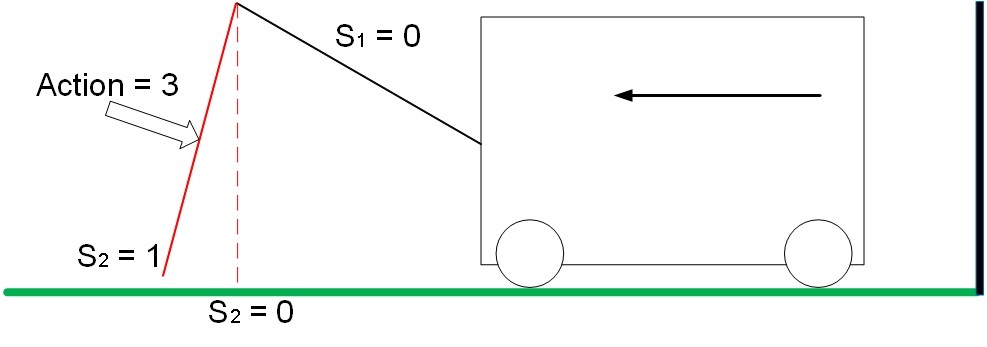
Fig. 7. Movement system with a positive reward
In the position S1 = 0, S2 = 0, action 2 drives the trolley to the wall, the system receives a negative reward equal to the change in distance from the wall. In our example, the reward is -1.

Fig. 8. Movement of a system with a negative reward.
Under other conditions and any actions of the “drive”, the system will stand still and the reward will be equal to 0.
It should be noted that the stable dynamic state of the system will be the sequence of actions 0-2-1-3 from the state S1 = S2 = 0, in which the cart will move in the positive direction with the minimum number of actions expended. Raised the knee - unbent the knee - lowered the knee - bent the knee = trolley moved forward, repeat. Thus, using the machine learning method, it is necessary to find the state of the system, such a specific sequence of actions, the reward for which will not be received immediately (actions 0-2-1 - reward for which is 0, but which are necessary to obtain 1 for the subsequent action ).
The basis of the Q-Learning method is the system state weights matrix. The Q matrix is a combination of all possible system states and weights of the system response to various actions.
In this problem, possible combinations of system parameters are 36 = 6 ^ 2. In each of the 36 states of the system, it is possible to perform 4 different actions (Action = 0,1,2,3).
Figure 9 shows the initial state of the Q matrix. The zero column contains the row index, the first row is the value of S1, the second is the value of S2, the last 4 columns are equal to the weights for actions equal to 0, 1, 2 and 3. Each row represents a unique system state.
During the initialization of the table, all values of the scales will be equal to 10.
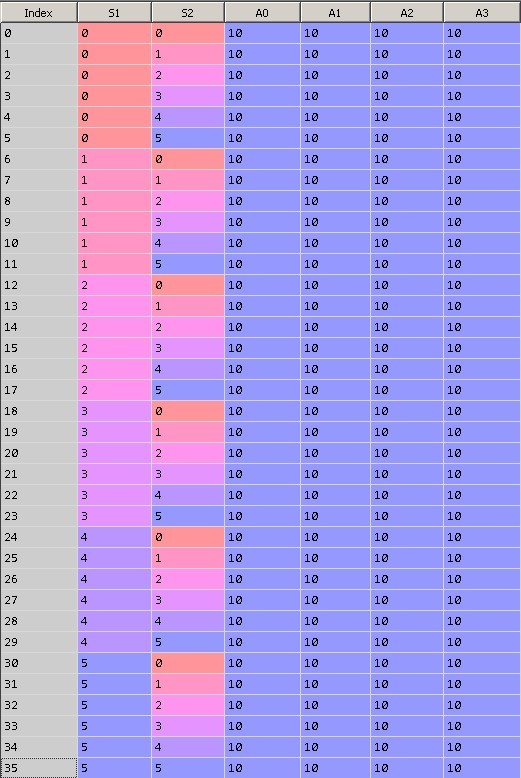
Fig. 9. Initialization of the Q matrix
After learning the model (~ 15000 iterations), the Q matrix has the form shown in Figure 10.

Fig. 10. Matrix Q after 15,000 iterations of learning
Please note that actions with weights equal to 10 are impossible in the system, therefore the value of the weights has not changed. For example, in the extreme position when S1 = S2 = 0, action 1 and 3 cannot be performed, since this is a limitation of the physical medium. These border actions are prohibited in our model, so the algorithm does not use 10-kts.
Consider the result of the algorithm:
...
Iteration: 14991, was: S1 = 0 S2 = 0, action = 0, now: S1 = 1 S2 = 0, prize: 0
Iteration: 14992, was: S1 = 1 S2 = 0, action = 2, now: S1 = 1 S2 = 1, prize: 0
Iteration: 14993, was: S1 = 1 S2 = 1, action = 1, now: S1 = 0 S2 = 1, prize: 0
Iteration: 14994, was: S1 = 0 S2 = 1, action = 3, now: S1 = 0 S2 = 0, prize: 1
Iteration: 14995, was: S1 = 0 S2 = 0, action = 0, now: S1 = 1 S2 = 0, prize: 0
Iteration: 14996, was: S1 = 1 S2 = 0, action = 2, now: S1 = 1 S2 = 1, prize: 0
Iteration: 14997, was: S1 = 1 S2 = 1, action = 1, now: S1 = 0 S2 = 1, prize: 0
Iteration: 14998, was: S1 = 0 S2 = 1, action = 3, now: S1 = 0 S2 = 0, prize: 1
Iteration: 14999, was: S1 = 0 S2 = 0, action = 0, now: S1 = 1 S2 = 0, prize: 0
Consider more:
Take iteration 14991 as the current state.
1. The current state of the system S1 = S2 = 0, this state corresponds to the line with the index 0. The highest value is 0.617 (we ignore the values equal to 10, described above), it corresponds to Action = 0. This means, according to the Q matrix at the system state S1 = S2 = 0 we perform the action 0. The action 0 increases the value of the angle of rotation of the servo S1 (S1 = 1).
2. The next state S1 = 1, S2 = 0 corresponds to the line with the index 6. The maximum weight value corresponds to Action = 2. We perform action 2 - increase S2 (S2 = 1).
3. The next state S1 = 1, S2 = 1 corresponds to the line with the index 7. The maximum weight value corresponds to Action = 1. We perform the action 1 - decrease S1 (S1 = 0).
4. The next state S1 = 0, S2 = 1 corresponds to the line with index 1. The maximum weight value corresponds to Action = 3. We perform action 3 - decrease S2 (S2 = 0).
5. As a result, they returned to the state S1 = S2 = 0 and earned 1 reward point.
Figure 11 shows the principle of choosing the optimal action.

Fig. 11.a. Q matrix

Fig. 11.b. Q matrix
Let us consider in more detail the learning process.
Full code on github .
Set the starting position of the knee to its highest position:
We initialize the Q matrix by filling in the initial value:
Calculate the parameter epsilon . This is the weight of the "randomness" of the algorithm in our calculation. The more iterations of learning passed, the less random values of actions will be selected:
For the first iteration:
Save the current state:
We get the "best" value of the action:
Consider the function in more detail.
The getAction () function returns the value of the action that corresponds to the maximum weight at the current state of the system. Take the current state of the system in the matrix Q and select the action that corresponds to the maximum weight. Note that this function implements a random action selection mechanism. With an increase in the number of iterations, the random choice of action decreases. This is done so that the algorithm does not get hung up on the first options found and could take another path that may turn out better.
In the initial initial position of the arrows, only two actions 1 and 3 are possible. The algorithm chose action 1.
Next, we define the row number in the Q matrix for the next state of the system, in which the system will go after performing the action that we received in the previous step.
In a real physical environment, after performing the action, we would be rewarded if movement followed, but since the trolley movement is modeled, it is necessary to introduce auxiliary functions of emulating the response of the physical environment to actions. (setPhysicalState and getDeltaDistanceRolled ())
Perform functions:
After performing the action, we need to update the coefficient of this action in the Q matrix for the corresponding system state. It is logical that if the action led to a positive reward, then the coefficient, in our algorithm, should decrease by a smaller value than with a negative reward.
Now the most interesting part is to look at the future to calculate the weight of the current step.
When determining the optimal action that needs to be performed in the current state, we choose the greatest weight in the Q matrix. Since we know the new state of the system into which we have passed, we can find the maximum weight value from the Q table for this state:
At the very beginning it is equal to 10. And we use the value of the weight of the action that has not yet been performed to calculate the current weight.
Those. we used the weight of the next step to calculate the weight of the current step. The greater the weight of the next step, the less we will reduce the weight of the current one (according to the formula), and the current step will be preferable next time.
This simple trick gives good results for the convergence algorithm.
This algorithm can be extended to a larger number of degrees of freedom of the system (s_features), and a larger number of values that the degree of freedom (s_states) takes, but within small limits. Fast enough, the Q matrix will take up all the RAM. Below is an example of a code for constructing a pivot matrix of states and weights of a model. When the number of "arrows" s_features = 5 and the number of different positions of the arrow s_states = 10, the Q matrix has dimensions (100000, 9).
This simple method shows the "wonders" of machine learning, when the model is learning nothing about the environment and learns the optimal state in which the reward for action is maximum, and the reward is awarded not immediately, for some action, but for the sequence of actions.
Thanks for attention!
Reinforcement training is a machine learning method in which a model is trained that has no knowledge of the system, but has the ability to perform some actions in it. Actions take the system to a new state and the model receives some reward from the system. Consider the work of the method on the example shown in the video. In the description of the video is the code for Arduino , which is implemented in Python .
Task
Using the “reinforcement training” method, it is necessary to teach the trolley to move away from the wall to the maximum distance. The award is presented in the form of the value of changing the distance from the wall to the trolley during movement. Measurement of the distance D from the wall is made by a range finder. The movement in this example is possible only at a certain offset of the “drive” consisting of two arrows S1 and S2. Arrows are two servo with guides connected in the form of "knee". Each servo in this example can be rotated by 6 identical angles. The model has the ability to perform 4 actions that represent the control of two servo drives, action 0 and 1 rotate the first servo at a certain angle clockwise and counterclockwise, action 2 and 3 rotate the second servo drive at a certain angle clockwise and counterclockwise. Figure 1 shows the working prototype of the trolley.
')

Fig. 1. Prototype carts for machine learning experiments
In Figure 2, the S2 arrow is highlighted in red, the S1 arrow is highlighted in blue, and 2 servo actuators in black.

Fig. 2. Engine system
The system diagram is shown in Fig. 3. The distance to the wall is marked D, the yellow shows the range finder, the system drive is highlighted in red and black.

Fig. 3. System diagram
The range of possible positions for S1 and S2 is shown in Figure 4:

Fig. 4.a. S1 boom range

Fig. 4.b. S2 boom range
The limiting positions of the drive are shown in Figure 5:
When S1 = S2 = 5, the maximum distance from the ground.
When S1 = S2 = 0, the minimum distance to the ground.

Fig. 5. Border positions of arrows S1 and S2
The "drive" 4 degrees of freedom. The action (action) changes the position of the arrows S1 and S2 in space according to a certain principle. Types of actions are shown in Figure 6.

Fig. 6. Types of actions (Action) in the system
Action 0 increases the value of S1. Step 1 reduces the value of S1.
Step 2 increases the value of S2. Step 3 reduces the value of S2.
Motion
In our task, the cart is driven only in 2 cases:
In position S1 = 0, S2 = 1, action 3 drives the trolley away from the wall, the system receives a positive reward equal to the change in distance from the wall. In our example, the reward is 1.

Fig. 7. Movement system with a positive reward
In the position S1 = 0, S2 = 0, action 2 drives the trolley to the wall, the system receives a negative reward equal to the change in distance from the wall. In our example, the reward is -1.

Fig. 8. Movement of a system with a negative reward.
Under other conditions and any actions of the “drive”, the system will stand still and the reward will be equal to 0.
It should be noted that the stable dynamic state of the system will be the sequence of actions 0-2-1-3 from the state S1 = S2 = 0, in which the cart will move in the positive direction with the minimum number of actions expended. Raised the knee - unbent the knee - lowered the knee - bent the knee = trolley moved forward, repeat. Thus, using the machine learning method, it is necessary to find the state of the system, such a specific sequence of actions, the reward for which will not be received immediately (actions 0-2-1 - reward for which is 0, but which are necessary to obtain 1 for the subsequent action ).
Q-Learning Method
The basis of the Q-Learning method is the system state weights matrix. The Q matrix is a combination of all possible system states and weights of the system response to various actions.
In this problem, possible combinations of system parameters are 36 = 6 ^ 2. In each of the 36 states of the system, it is possible to perform 4 different actions (Action = 0,1,2,3).
Figure 9 shows the initial state of the Q matrix. The zero column contains the row index, the first row is the value of S1, the second is the value of S2, the last 4 columns are equal to the weights for actions equal to 0, 1, 2 and 3. Each row represents a unique system state.
During the initialization of the table, all values of the scales will be equal to 10.

Fig. 9. Initialization of the Q matrix
After learning the model (~ 15000 iterations), the Q matrix has the form shown in Figure 10.

Fig. 10. Matrix Q after 15,000 iterations of learning
Please note that actions with weights equal to 10 are impossible in the system, therefore the value of the weights has not changed. For example, in the extreme position when S1 = S2 = 0, action 1 and 3 cannot be performed, since this is a limitation of the physical medium. These border actions are prohibited in our model, so the algorithm does not use 10-kts.
Consider the result of the algorithm:
...
Iteration: 14991, was: S1 = 0 S2 = 0, action = 0, now: S1 = 1 S2 = 0, prize: 0
Iteration: 14992, was: S1 = 1 S2 = 0, action = 2, now: S1 = 1 S2 = 1, prize: 0
Iteration: 14993, was: S1 = 1 S2 = 1, action = 1, now: S1 = 0 S2 = 1, prize: 0
Iteration: 14994, was: S1 = 0 S2 = 1, action = 3, now: S1 = 0 S2 = 0, prize: 1
Iteration: 14995, was: S1 = 0 S2 = 0, action = 0, now: S1 = 1 S2 = 0, prize: 0
Iteration: 14996, was: S1 = 1 S2 = 0, action = 2, now: S1 = 1 S2 = 1, prize: 0
Iteration: 14997, was: S1 = 1 S2 = 1, action = 1, now: S1 = 0 S2 = 1, prize: 0
Iteration: 14998, was: S1 = 0 S2 = 1, action = 3, now: S1 = 0 S2 = 0, prize: 1
Iteration: 14999, was: S1 = 0 S2 = 0, action = 0, now: S1 = 1 S2 = 0, prize: 0
Consider more:
Take iteration 14991 as the current state.
1. The current state of the system S1 = S2 = 0, this state corresponds to the line with the index 0. The highest value is 0.617 (we ignore the values equal to 10, described above), it corresponds to Action = 0. This means, according to the Q matrix at the system state S1 = S2 = 0 we perform the action 0. The action 0 increases the value of the angle of rotation of the servo S1 (S1 = 1).
2. The next state S1 = 1, S2 = 0 corresponds to the line with the index 6. The maximum weight value corresponds to Action = 2. We perform action 2 - increase S2 (S2 = 1).
3. The next state S1 = 1, S2 = 1 corresponds to the line with the index 7. The maximum weight value corresponds to Action = 1. We perform the action 1 - decrease S1 (S1 = 0).
4. The next state S1 = 0, S2 = 1 corresponds to the line with index 1. The maximum weight value corresponds to Action = 3. We perform action 3 - decrease S2 (S2 = 0).
5. As a result, they returned to the state S1 = S2 = 0 and earned 1 reward point.
Figure 11 shows the principle of choosing the optimal action.

Fig. 11.a. Q matrix

Fig. 11.b. Q matrix
Let us consider in more detail the learning process.
Q-learning algorithm
minus = 0; plus = 0; initializeQ(); for t in range(1,15000): epsilon = math.exp(-float(t)/explorationConst); s01 = s1; s02 = s2 current_action = getAction(); setSPrime(current_action); setPhysicalState(current_action); r = getDeltaDistanceRolled(); lookAheadValue = getLookAhead(); sample = r + gamma*lookAheadValue; if t > 14900: print 'Time: %(0)d, was: %(1)d %(2)d, action: %(3)d, now: %(4)d %(5)d, prize: %(6)d ' % \ {"0": t, "1": s01, "2": s02, "3": current_action, "4": s1, "5": s2, "6": r} Q.iloc[s, current_action] = Q.iloc[s, current_action] + alpha*(sample - Q.iloc[s, current_action] ) ; s = sPrime; if deltaDistance == 1: plus += 1; if deltaDistance == -1: minus += 1; print( minus, plus ) Full code on github .
Set the starting position of the knee to its highest position:
s1=s2=5. We initialize the Q matrix by filling in the initial value:
initializeQ(); Calculate the parameter epsilon . This is the weight of the "randomness" of the algorithm in our calculation. The more iterations of learning passed, the less random values of actions will be selected:
epsilon = math.exp(-float(t)/explorationConst) For the first iteration:
epsilon = 0.996672 Save the current state:
s01 = s1; s02 = s2 We get the "best" value of the action:
current_action = getAction(); Consider the function in more detail.
The getAction () function returns the value of the action that corresponds to the maximum weight at the current state of the system. Take the current state of the system in the matrix Q and select the action that corresponds to the maximum weight. Note that this function implements a random action selection mechanism. With an increase in the number of iterations, the random choice of action decreases. This is done so that the algorithm does not get hung up on the first options found and could take another path that may turn out better.
In the initial initial position of the arrows, only two actions 1 and 3 are possible. The algorithm chose action 1.
Next, we define the row number in the Q matrix for the next state of the system, in which the system will go after performing the action that we received in the previous step.
setSPrime(current_action); In a real physical environment, after performing the action, we would be rewarded if movement followed, but since the trolley movement is modeled, it is necessary to introduce auxiliary functions of emulating the response of the physical environment to actions. (setPhysicalState and getDeltaDistanceRolled ())
Perform functions:
setPhysicalState(current_action); - we simulate the reaction of the medium to the action chosen by us. Change the position of the servos, shift the cart. r = getDeltaDistanceRolled(); - We calculate the reward - the distance traveled by the cart.After performing the action, we need to update the coefficient of this action in the Q matrix for the corresponding system state. It is logical that if the action led to a positive reward, then the coefficient, in our algorithm, should decrease by a smaller value than with a negative reward.
Now the most interesting part is to look at the future to calculate the weight of the current step.
When determining the optimal action that needs to be performed in the current state, we choose the greatest weight in the Q matrix. Since we know the new state of the system into which we have passed, we can find the maximum weight value from the Q table for this state:
lookAheadValue = getLookAhead(); At the very beginning it is equal to 10. And we use the value of the weight of the action that has not yet been performed to calculate the current weight.
sample = r + gamma*lookAheadValue; sample = 7.5 Q.iloc[s, current_action] = Q.iloc[s, current_action] + alpha*(sample - Q.iloc[s, current_action] ) ; Q.iloc[s, current_action] = 9.75 Those. we used the weight of the next step to calculate the weight of the current step. The greater the weight of the next step, the less we will reduce the weight of the current one (according to the formula), and the current step will be preferable next time.
This simple trick gives good results for the convergence algorithm.
Algorithm scaling
This algorithm can be extended to a larger number of degrees of freedom of the system (s_features), and a larger number of values that the degree of freedom (s_states) takes, but within small limits. Fast enough, the Q matrix will take up all the RAM. Below is an example of a code for constructing a pivot matrix of states and weights of a model. When the number of "arrows" s_features = 5 and the number of different positions of the arrow s_states = 10, the Q matrix has dimensions (100000, 9).
Increasing the degrees of freedom of the system
import numpy as np s_features = 5 s_states = 10 numActions = 4 data = np.empty((s_states**s_features, s_features + numActions), dtype='int') for h in range(0, s_features): k = 0 N = s_states**(s_features-1-1*h) for q in range(0, s_states**h): for i in range(0, s_states): for j in range(0, N): data[k, h] = ik += 1 for i in range(s_states**s_features): for j in range(numActions): data[i,j+s_features] = 10.0; data.shape # (100000L, 9L) Conclusion
This simple method shows the "wonders" of machine learning, when the model is learning nothing about the environment and learns the optimal state in which the reward for action is maximum, and the reward is awarded not immediately, for some action, but for the sequence of actions.
Thanks for attention!
Source: https://habr.com/ru/post/308094/
All Articles