Procedural generation of levels for puzzle games

If you have already tried to create your own puzzle game, you may have already understood that the implementation and coding of game rules are quite simple, but creating levels is a difficult and lengthy job. Or even worse - you spent a lot of time creating several levels, trying to insert certain tasks into them, but when your friends tried to play them, they completed these levels in a completely different way or with such simple tricks that you didn’t even think about them.

It would be great to find a way to make the computer save you time and solve the problems I mentioned above ... And this is where procedural generation comes to the rescue!

It must be said that there is for example only one way to sum up the vectors, and any programmer who needs it should follow the same rules; however, in the case of procedural generation, you are completely free. There are no right and wrong ways. The main thing is the result.
')

Fruit Dating - rules and features

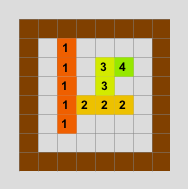
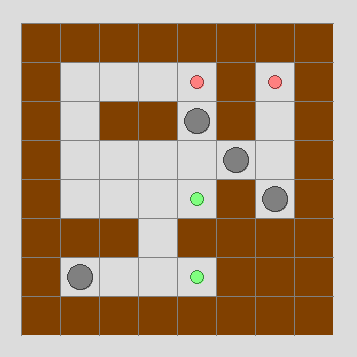
Not so long ago, we released Fruit Dating game for iOS devices (it is also available for Android and even for unreleased (at the time of the game's release) Tizen). This is a puzzle game with simple rules. Its goal is to connect pairs of fruits of the same color by swiping your finger across the screen. Moving your finger corresponds to the slope of the playing field in the desired direction. When a player tries to complete his task, various obstacles such as stones, cars and other fruits stand in his way. All moving objects move in one direction. The pictures below show the first level, in which 3 moves are required to connect the fruit.





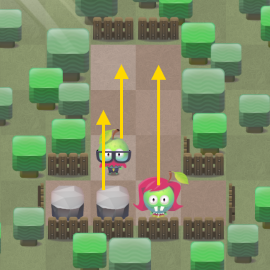
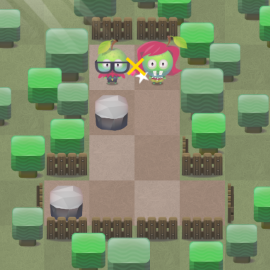
Over time, new features are added:

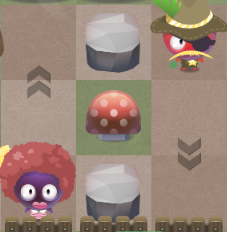	One-way passes are placed on the border of the tile and limit the direction in which objects can be moved.
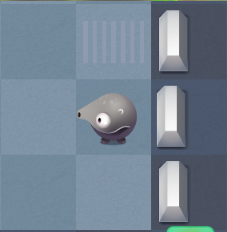	Anteaters can look in different directions, but this direction is constant and does not change during the level. When the fruit is in the direction of the anteater's gaze, it “shoots” with its tongue and attracts the fruit to itself.
	Stones, cars and barrels can move through the puddles, but not fruits. When a fruit falls into a puddle, it becomes dirty, and the date is canceled for it!
	A sleeping hedgehog is on the tile and wakes up when something hits him. If it hits a barrel, a stone or a car, he falls asleep again because they are inedible. But when a fruit hits him, the hedgehog eats him.

You probably already noticed that the level consists of tiles; this simplifies the work, because each level can be represented as a small grid. Its maximum size is 8x8 tiles, but there is always a fixed border, so that a “useful” area is not larger than 6x6 tiles. This may not seem like much, but it has been proven that quite complex tasks can be created for such a field.

Based on the basic rules (since additional features were added later), I began to create my own generator. At first, I certainly thought that someone in the world had already solved a similar problem, so I began to search the Internet for procedural generation of puzzle levels. It turned out that this question was not considered very widely. I found only a few useful articles for me. Basically they were devoted to generating / solving levels for Sokoban. For example:

One and two .

It was also interesting that most of them were written by scientists (professors of Sokoban :-)). I learned two principles from these articles: first, when randomly generating something, it is good to introduce a little symmetry so that people perceive the results more positively. Secondly, the choice of algorithm depends on you, but none of them is perfect.

Puzzle solving tool

Obviously, each generated level must be tested (to see if it can be solved, and how difficult it is to do it), so first I decided to create a tool for solving levels. Since at that time I considered only the basic rules without additional features, I had the following ideas for the “solver”:

a) from the starting position you can start moving in any direction (left, right, up, down);
b) from the next position you can continue in any direction again;
c) in any position, the compounds of the fruit are checked, the matched fruits are removed from the field and b) is continued until several fruits remain on the field.

As you can see, this is a simple brute force approach. So, the number of possible positions on the field was: 4, 4 * 4 = 4 ² , 4 * 4 * 4 = 4 ³ , ... 4 ⁿ . On move 10, there were more than a million combinations of the field, and on move 25, there were 1,125899906842624 combinations. Well, then we can limit the maximum number of moves, say 10, and we will not be interested in more difficult levels, but there is another danger here. Some of the puzzles can be created or generated in such a way that the player who made some bad moves at the beginning cannot complete the level. Or in some levels there may be an obsession of states on the field. If the algorithm branches in such a direction too early, the level can be marked as unsolvable, even if there are shorter branches with a simpler solution. Also, if the algorithm has found a solution, there are no guarantees that it is the shortest - you need to complete all the branches in order to find the shortest solution. In addition, there are often states on the field that one move in a certain direction does not change anything. Look at the third picture in the part “Fruit Dating - rules and features” - nothing will change if we move to the left.

Therefore, the rules have changed:

a) from the current position try to move in any direction;
b) if the state on the field has changed, check whether the state is new or has already been;
c) if the state is new, save it along with the depth of the solution (the number of moves needed to fall into that state);
d) if there was such a state earlier, and the depth of the solution was equal to or less than the current one, delete the current branch. Otherwise, replace the old state (because we got into it through a smaller number of moves) and continue.

There are also other rules, for example, checking the coincidence of fruits and the termination of the whole process when a solution is found; in addition, later there were other rules related to additional features, but I described the basic tool for the solution. He quickly breaks off whole branches without a solution. In addition to the depth of the solution, it also checks the parent positions stored for each state on the field, so that at the end you can easily print the solution. Let's look at this on the example of the first level of the game:


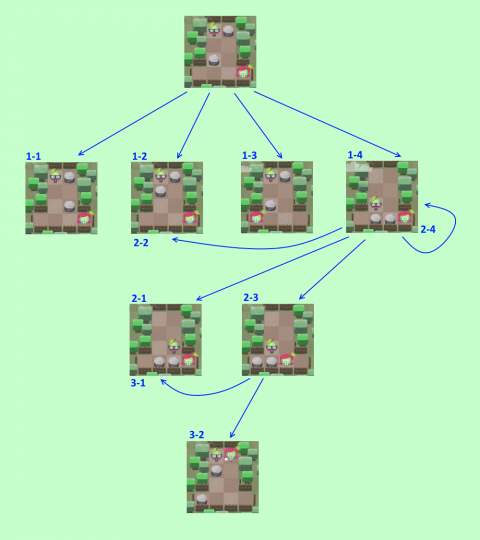
From the initial position, the moves branch into four possible directions. Mark them as 1-1, 1-2, 1-3, 1-4. The algorithm always tends to move in the following order: right, up, left, down. Since for further study of the stored states it is necessary to apply the stack, the first continuing state is transferred to the stack last (in our case, 1-4). Again, the first move is a right shift (2-1) and since this is a new state, it is written to the stack. The next step is an upward shift, which leads to state 2-2. We were already in this state in the first iteration. Therefore, we apply rule d) and terminate this branch — nothing is written to the stack. Next is the attempt to move to the left. It leads to a new state (2-3) and it is pushed onto the stack. The last move is a downward shift, but there is no difference between 1-4 and 2-4, so we don’t put anything on the stack (rule b) ... no new state = we don’t do anything). Now the top state of the stack is 2-3. From it, we move to the right and fall into the 3-1 state, which is equal to the 2-1 state. But in 2-1 we were at the second iteration, so we cut off this branch. Then we move up, the fruit is on the adjacent tiles, and since it was the only pair, the game ends.

The algorithm works, although it may not find the shortest path. He simply takes the first solution found. To fix this, I first limited the maximum number of moves to 30. If the solution is not, I consider the level impassable. If the solution is found, let's say on move 15, I launch the “solver” again with a maximum depth of solution 14 (15 - 1). If the solution is not, then 15 is the shortest path. If a solution is found for example on move 13, I run the tool with a maximum depth of 12 (13 - 1). I continue the process until any decision returns. The last returned solution is the shortest solution.

Generator

We have created a "solver", now you can go to the generator and check with it every generated puzzle.

The generation phase consists of two parts:

• wall generation
• generating objects on the field

Generating walls always begins with drawing a fixed field border:


Random parameters are generated, indicating whether the wall will be painted one tile at a time, or two tiles. In the case of two tiles, random symmetry is generated. It tells you where the second tile should be located - whether it will be reflected vertically, horizontally, rotated 90 degrees or there will be a combination of transformations. In the first grid in the figure below, only one tile is filled at once. In all other grids, various examples of random symmetry of two tiles are presented:


The number of walls, their length and direction are random. Each wall starts from a random point on the border. Each wall is drawn in one or more iterations. After the first iteration, a number between 0 and (length of the wall) is randomly chosen - 1. If it is zero, the iteration cycle ends. If it is greater than zero, then this number becomes the length of the next part of the wall. A random point of the current part of the wall is selected, the direction is chosen randomly, orthogonal to the current part of the wall, then the next part of the wall is drawn. The result may look like this (numbers denote iterations):


The picture shows that each next part of the wall is shorter, so you can be sure that at some point the wall will end.

Since all the walls start from the border of the field, each individual tile was connected to the border. For me, it looked boring, so I added another step, which generated internal walls. Internal walls are not connected with any existing tile. The stage begins by selecting a random tile and checking whether it is free and tiles within 3x3 of it. If so, then the wall WILL be placed in the grid, and the next tile is selected according to a random direction (this direction is randomly selected before testing the first tile). The cycle is interrupted when the condition of free on 3x3 tiles is not met. Pay attention to the word “will” highlighted above. If you put the wall in the grid right away and move on to the processing of the next tile, the area within 3x3 will never be free, because you have just placed the wall there. Therefore, I save all the tiles of the walls in a temporary array and at the same time place them in the grid after the termination of the cycle.

When generating walls, some of them may overlap each other, and it is very likely that small spaces will be created, or even the original area will be divided into several unconnected areas. Of course, we do not want this. Therefore, in the next step, I check which continuous area is the largest, and fill the rest with walls.

With this check, I go through the entire grid of the field and if the tile is free, I recursively fill its entire continuous area with the identifier of this area (the free tiles are tiles without a wall and not yet marked by the area identifier). After that, I again go through the whole field and count the tiles with each area ID. Finally, I once again go through the whole field and fill all the tiles with the area identifier with walls, with the exception of the area with the largest number of tiles.

The whole process of generating walls can be viewed in this animation. This shows the generation of walls and the generation of internal walls, and in the last frame, the void in the lower right corner is filled at the stage of areas merging:


After the walls are generated, you can start generating objects. We need at least one pair of fruit and zero or more obstacles (represented in the game by stones, cars, and barrels).

It will be good if the fruit is located in most cases in the corners, at the ends of the corridors and other similar places. Sometimes it may be interesting to place them in the middle of an open area, but the former is more preferable. To achieve this, we add the weight of each free tile in terms of the attractiveness of the location of the fruit on it.

For the ends of the corridors, surrounded by tiles on three sides, I chose a weight of 6 + Random (3). For tiles in horizontal or vertical corridors, I chose weight 2. For corners, I chose weight 3 + Random (3), and for free areas - 1.

Based on the weights, it is obvious that the most likely location of the fruit is at the ends of the corridors, then there is an arrangement in the corners, corridors and free areas. For each generated level, weights are generated only once.

Obstacles (stones, cars, barrels) are created in a similar way, but the difference is that their weights are separated from the scales of the fruit; there is also a certain random density of obstacles that indicates the number of obstacles in a level, if they are selected.

By the way, with the help of scales, you can do other tricks. Later I added a sleeping hedgehog and an anteater (their descriptions are given at the beginning of the article). It does not make sense to put them in the middle of the corridor, so for corridors their weight = 0.

This animation shows the location at the level of fruits and obstacles:


The final generated level is shown in the static image below. The solution requires 6 moves (right, up, left, down, right, up). Well, after 1-2 minutes after clicking on the Generate button, we have an interesting looking level, which can be completed in 6 moves (no one will play levels that require 30 moves to complete!); besides, for his search we did not have to suffer a bit. But ... you can always do a little bit better. And from this point in our article we will try to make the levels more beautiful.

Editor

Level generation completed in the previous section. Our editor supports drag & drop, so you can easily drag objects to get a higher level of symmetry. For example, like this:


After making changes, it is important to retest the level with a “solver”. Sometimes small changes can lead to undecided levels. In our example, the changes increased the number of moves to the solution from six to seven.

At this stage of manual editing, the approach to procedural generation of levels forks. If you need or want to apply changes manually, the level generator will serve you simply for tremendous time savings. If this stage is not required and you think that the generated levels are good enough, then the generator can be part of your final game. Players will be able to generate new levels on their own.

Final result

Procedural level generation saved us a tremendous amount of time. Despite the fact that the generator can create garbage - levels that are too easy or too difficult to pass, levels full of obstacles or ugly levels - it still saved us a lot of time. He also allowed us to choose and discard some of the unlearned levels. If we made them by hand, it would take months of work. Here's how the levels generated in this article look like in the final game:


About the author: Tomas Rychnovsky is an indie developer of small mobile games for Android, iOS and Tizen.