Model of watercraft interaction in video games

Let's talk about vehicle physics.

The physics of vehicles in video games is not very much discussed. Articles on the Internet about the physics of transport in video games are few and superficial; they are usually devoted to the very basics. The transport programmer for video games feels today in a relative vacuum. Perhaps this situation has arisen, because this topic is rather difficult to explain, and maybe we are just ashamed to admit the use of hacks, simplifications and tricks that we bring in comparison with the “correct”, realistic simulation of physics. No matter how it was, video games have unique problems in the simulation of transport, and therefore it is worth writing about it. This is an exciting topic related to physics, working with the camera, sound, special effects, as well as to human perception and psychology.

I decided to first talk about the courts, because I recently worked with them; I also discovered that their dynamics are not completely understood even at the level of research (although much is understandable). Models and theories are formulated in such a way that it becomes difficult to apply them directly in video games. Or they require very resource-intensive simulation methods that are almost impossible to control and adapt to the bizarre needs of developers and players. But you can write a simplified model that takes into account the important parameters of the vessel. There is definitely a bit of art, a "leap of faith" and a small amount of "creative" physics that will make Kelvin and Stokes roll over in graves.

Series of articles on the physics of ships

In this series, I will present an algorithm for calculating the most important forces acting on a ship in water. First of all, I strive to create a model that describes the main dynamic characteristics of the behavior of ships on water, without addressing the complex and resource-intensive calculation of fluid dynamics.
')
I will limit myself to reasonable performance costs, for example, less than 1 ms per ship. The model should be sufficiently universal to simulate the behavior of vessels of various sizes and shapes in conditions from calm to storm.

In the first article of this series, we will work with hydrostatic forces, and also lay an important foundation for calculating all other forces involved in the model. Other forces are the dynamic forces resulting from the movement of the vessel relative to the water. They will be discussed in the following articles.

Meet the buoyancy

Before delving into the algorithm itself, I want to talk a little bit about pushing. All that is enough for us to do is to calculate the magnitude and point of application of the buoyancy force to the body partially immersed in the liquid.

When the body is immersed in a fluid, due to the pressure of the fluid, it exerts a force on the surface of the body. The more pressure, the more power. Strength is the result of the movement of a multitude of water particles in a fluid that elastically hits the surface of the body (like perfect billiard balls). This is a microscopic force, the impact of which is felt even if the water does not move in any particular direction (current) and if the vessel remains stationary; therefore, it is called hydrostatic force. The total force of all these atoms or molecules hitting the surface is perpendicular to the surface. It should also be mentioned that the pressure in water increases at depth (on a planet with gravity), since the greater depth implies that more and more water presses down with its weight. However, the pressure itself does not have a definite direction, and even if there is no liquid directly above some point of water, the pressure at this point will still depend on the total depth nearby. ( * )


Increasing the force during immersion is very important for pushing, since the resulting pushing force arises due to the imbalance of the vertical component of hydrostatic forces on the surface of the body. The horizontal component of hydrostatic forces is always balanced. This is intuitively understandable - for each individual elementary (closed) volume, it is always possible to find at the same depth an elementary area, directed in the opposite direction. Since the values ​​of hydrostatic forces are the same, but directed in opposite directions, they are balanced. On the other hand, the vertical component of the hydrostatic forces is not balanced. In the general case, since the volume is closed, the surfaces whose normals are directed downward are usually at a greater depth than the surfaces whose normals are directed upwards. Therefore, the pressure forces acting on the surface with downward normals prevail. The force of pressure acts in the opposite direction to the normals, the resultant force is directed upwards and it can be proved [ 2 ] that its value is equal to “the weight of the displaced fluid” (the weight of the volume of the body filled with water).

We still lack one puzzle piece: so that all of the above leads to pushing, we also need to specify the point of application of hydrostatic force. The point of application of the buoyancy force is the point relative to which the moments of all hydrostatic forces are balanced. If we continue the reasoning based on the elementary areas of the submerged body, everything will become a little less obvious. Since hydrostatic forces increase with greater immersion, the point of application of hydrostatic force to a given horizontal surface is generally lower than the center of the surface. As shown in Appendix A, using the example of a submerged triangle (this is a convenient example, because in games objects usually consist of triangles), the point of application of force is always below the center. Despite the fact that the sum of all moments of all applied forces is usually below the center of any surface, it is still balanced near the center of gravity of the volume. A formal proof of this is given in [ 2 ] using the Ostrogradsky-Gauss theorem ( ** ), or the divergence theorem. This can also be verified numerically. I mention this because if you decide to divide the body into small planes, such as triangles, and summarize all hydrostatic forces and their moments, the temptation arises to simplify the calculation of moments, as if the elementary forces for each triangle are attached to its center (which is easy to find ).

However, if you do this, you will get the wrong result. The force will be calculated correctly, but there will be a residual moment relative to the center of the submerged volume, while the vessel can tilt at rest even on a completely flat surface of the water. This is especially true when using a low-poly mesh object to reduce performance damage, because the error made for each triangle is quite significant. On the other hand, with a large number of small triangles, the error caused by the simplification is significantly reduced, and the simplification may become quite acceptable. But there is always a trade-off between the difficulty of calculating the correct center and the number of triangles in the object. Appendix A provides a formula for calculating the location of the point of application of hydrostatic forces on a triangle immersed in a liquid.

Two ways to flip the boat

In light of the above, there are two ways to calculate the pushing force. Volumetric method: by calculating the immersed volume and determining its center of gravity. Surface method: by determining the immersed surface and the calculation of the force applied to it. These two methods, when properly applied, should give the same result.

Both the volumetric and surface methods without too much approximation require the determination of the coordinates of the intersection of water with the hull. It looks threatening, especially if we assume that water has a non-flat surface: the calculation looks too resource-intensive and complex. Perhaps that is why many are inclined to use volume primitives. For example, spheres: in contrast to the calculation of the intersection of the surface of water with a complex figure, the calculation of the volume of the part of the sphere immersed in water is quick and simple if you take the water in close proximity to the sphere flat. The volume can even be determined analytically, which means (at least theoretically), the calculation with infinite precision, or with the accuracy allowed by floating point operations (yes, there are many wordplay in this article). It also seems that the submerged volume will change gradually and smoothly when the ship is raised and lowered in water, and the constancy of the physical model is often preferred in games.

But approximating the hull of a standard vessel with the help of spheres can quickly turn into a nightmare, because many spheres of different diameters are required. Since the spheres are one of the worst options for packing densely in a volume, you will have significant voids between the spheres (Figure 1). There is an upper limit on the density of packing in the volume, even for spheres with different radii [ 5 ]. The presence of these voids leads to a noticeable impermanence when pushing. Spheres can be made intersecting, but then the calculated immersed volume will be more than the real one. Finally, while calculating the intersection of a flat surface with a sphere is simple, calculating the intersection of a sphere with an arbitrary water surface is much more difficult, so we can try to find a solution to calculate the intersection of a ship's hull with water.


Figure 1 - Approximation of vessel volume using spheres is not a solution.

Body volume can be converted to voxels, i.e. approximate by a set of simple volume primitives, for example, cubes. Voxels intersecting with water can also be converted into smaller voxels until the desired accuracy is achieved. The problem with volume approximations is that they give (fairly coarse) answers to the question “how much water is displaced?”, But it is rather useless for determining the waterline of a submerged object, which is needed, for example, to apply special effects of water, such as splashes and foam , or to determine the shape of the surface in contact with water, unless of course you use a completely unacceptable number of them.

Assuming that we can accurately calculate the surface of the body, immersed in water, we still have a choice between the volumetric and surface methods of calculation. For the volumetric method, we must close the submerged surface of the body to create a closed volume, calculate its full volume and center of gravity, and then apply a pushing force to it. With the surface method, we calculate the hydrostatic pressure forces acting on each submerged surface element (triangle), and summarize their linear impulses and angular momentum around the center of gravity of the body.

The advantage of the surface method is that it does not need to close the volume, everything is ready for the direct summation of forces. With the volumetric method, the immersed volume may also consist of several volumes. It is convenient to use it, for example, for the calculation of catamaran hulls. However, even if the vessel does not have openings, the intersection with water should represent the closure of two or more volumes, and we must determine which of the volumes each of the immersed triangles belong to, which is an additional difficulty in calculating this method. The surface approach in this respect is more versatile, it works regardless of the number and shape of the formed volumes, and it does not require a circuit. That is what I chose for my algorithm.

Algorithm structure

I will explain in general terms the structure of the algorithm with some important simplifications that will provide a quick calculation and at the same time sufficient results.

The first assumption that I will make is that the surface of the water is described by a grid of triangles whose vertices move with each frame in accordance with the movement of water. Of course, this is not always the case, but it is always possible to approximate the surface of the water through a grid of triangles. Later in this article I will tell you how to take the surface of the water and prepare for it a representation in the form of a grid of triangles around the body.

The main task will be to determine the coordinates of the intersection between the surface of the water and the surface of the hull. Having reviewed the implementation of Edouard Halbert [ 1 ], I began to implement the exact solution, taking into account all the options for crossing the water surface and the triangle. This problem is quite complex, because in theory there are many ways to separate a triangle by a surface. A surface can cut through one triangle in several places, pass through the center, without touching either side, or plunging into any of the vertices. Each such submerged area must be divided into triangles (triangulated), but these areas are not necessarily convex, so they are more difficult to triangulate. In addition, such cases are quite frequent. Even in relatively calm water, they occur very often and must be processed in such a way that they do not lead to unrealistic discreteness in the size of surfaces considered immersed. After working for some time on the implementation of an absolutely accurate, but very slow algorithm for calculating intersections, I realized that I needed to find ways to simplify the algorithm, while not sacrificing too much of its overall behavior. The algorithm I presented here is the result of such simplifications. I will not tell the details of the first (exact) algorithm, because it is extremely tedious and boring; In addition, the optimized algorithm works fine and calculates the order of values ​​faster.

The optimized algorithm has the following structure: a floating body is approximated using a grid of triangles (its body). We determine the height above the water of each vertex of this hull. If the height is negative, then the body is immersed in water. Triangles, all three peaks located above the water, are considered to be completely not immersed in water. This simplification, in reality, water may be above the surface of the triangle, but below all three vertices (see Figure 4). We also consider a triangle completely submerged, if all three vertices are under water, despite the fact that some of the water may be under the triangle on some part of its area. If only one or two vertices are under water, we divide the triangle into one area under water and one area above water, as shown in Figure 2. If the area under water is not a triangle, we triangulate it. I made a bold (and theoretically incorrect) assumption that the surface of the water crosses the side of the triangle between the submerged and surface peaks only once. Figure 3 shows examples of cases where the intersection is not calculated accurately. At the end we get a list of triangles, each of which is submerged under water. Then we calculate the hydrostatic and hydrodynamic forces acting on these triangles.


Figure 2 - 4 simplified cases of intersection of triangles with a section of water. From left to right at the triangles are immersed in water, respectively, 0, 1, 2 and 3 vertices. With 2 submerged vertices, we need to once again triangulate the submerged part. It should be noted that the intersection with water is not exact due to another simplification, which we will consider.


Figure 3 - Three examples of cases incorrectly handled by an optimized algorithm. Red areas are indicated by triangles that should be considered under water but not counted. The two triangles on the left intersect with water, but none of their peaks is under water. The middle triangle is shown in perspective; it does not intersect with water on either side, but the top of the wave passes through the middle of the triangle. At the right triangle, there are two peaks under the water, but the water is also under the triangle on the side between these two peaks.


Figure 4 - An example of a case that often occurs when ripples on the water. The larger right lower triangle of the body intersects water in several areas, one of which does not intersect either side of the triangle. Worse, the intersected areas could be concave, and fast triangulation would be even more complicated. Handling all such cases would lead to development time and performance when the game is running. In addition, it is quite meaningless, because, strictly speaking, the surface of the water itself changes due to the presence of the vessel.

For a ship model, such cases are less important than it seems. In practice, sacrificing accuracy is not a problem if the size of the body triangles is not too large relative to the amplitude and wavelength of the smallest waves that we want to take into account.

The main advantage of the proposed approach is that all vertices can be processed in the first pass, regardless of which of the three form a triangle. After that, all the information needed to process each triangle, which serves as the basis for 0, 1 or 2 immersed triangles, becomes available. The triangle intersection part is very simple and fast. Most processing can easily be parallelized if necessary. We also know the maximum number of immersed triangles that can be obtained: twice the number of triangles of the object's body. This allows us to allocate all the memory in advance in a simple array.

In the next section, we will look at important implementation details, such as a method for approximating the surface of water to optimize the determination of water depth, a method for accurately separating a triangle, only one or two vertices of which are under water, as well as the calculation of buoyancy forces.

Implementation details

Water section

To determine the height above the water of each peak, we need a quick way to determine the position of the water below a given point. It largely depends on the method of simulating water in a game or in its simulation. If the water is flat or described by a simple function, it can be a quick way to simply determine the height of the water, measuring or evaluating it with each request. However, in other cases, the algorithm for determining the height of water is resource-intensive and only a limited number of requests can be made. For example, this happens in the case of methods based on fast Fourier transform, such as Tessendorf waves [ 4 ].

In this case, I propose to measure the height of water once at points at the same distance from the body, thus creating a height map, which will then be used for all subsequent height requests. I will call this elevation map the “waterway”. The water section should be at least not less than the vertical projection of the body. For example, you can start with a square section of water, whose side is equal to the diagonal of a rectangle, described around the projection. Like the traditional elevation map, the water section consists of a rectangular area divided into stripes, forming rows and columns intersecting in square cells (Figures 5 and 6). Each cell itself is divided into 2 triangles. For each triangle, we calculate the equation of the surface on which it is located, which allows us to quickly determine the projection of a point on it.


Figure 5 - Section of water size 4x4 and waterline (blue), shown below.


Figure 6 - Section of water size 5x5 and waterline (blue), shown below.

Cutting algorithm

When part of the vertices of the triangle is under water, and part is above water, we need to cut it into a piece completely submerged under water, and a piece completely above the water. There is a way to simplify cutting, fast in calculations and continuous. By “continuity,” I mean the absence of situations where a small change in the height of the peaks leads to unexpectedly strong changes in the submerged area. This problem did not arise if we precisely cut the triangles into underwater and surface parts, it appears only because of the approximation, and we need to choose the method that behaves well. This problem became one of my first obstacles, and sometimes leads to instability in pushing out, when the body suddenly begins to jump out or sink significantly, destroying the whole effect.






Figure 8 - Simplified cutting of a triangle when there are two vertices above the water.

Calculation of hydrostatic forces

After the cutting algorithm was performed for all the triangles of the mesh object, we received a list of fully immersed triangles. The buoyant force acting on the body is the sum of all hydrostatic forces acting on each immersed triangle.Since we are considering a linear force, we can only summarize the vertical component of the hydrostatic force, because we have seen that the other forces balance each other. The force acting on the immersed triangle is:



Do not forget that the application of hydrostatic force to the center of the triangle instead of the actual center of its application leads to residual torque relative to the center of the displaced volume. If the number of triangles is small and it is important not to receive any torque, then it is necessary to calculate the point of application of force to the triangle. Appendix A presents the formula for determining the center of application of hydrostatic force to two types of triangles, whose base is horizontal, and the top is directed up or down. A randomly immersed triangle should be cut into two such triangles, after which two sets of hydrostatic forces and centers of application of forces are calculated and summed.

We put everything together

Figure 10 provides a brief description of the algorithm.


Figure 10 - Algorithm diagram.

So, we can summarize the structure of the algorithm as follows (we have assumed that x / z is a horizontal plane, and y is the vertical axis directed upwards):

• At each simulation step, we update the position of the water section to follow the floating body. As you can see from the animated gif in Figure 11, the stretch of water does not follow smoothly behind the vessel. When a ship moves horizontally, it shifts from its original position so that the water section loses a row (or column) on one side and adds a row (or column) on the other side. When this happens, the coordinates of the water section (say, its southwest corner) change dramatically compared to the previous step.
  
  
• After determining the coordinates of the water section for each water grid point, the water height is determined or calculated.
  
  
• , , y , . , .
  
  
• , , .
  
  
• , , 0, 1 2 .
  
  
• ( ).
  

Of course, we can apply many different ways to optimize. For example, we can first vertically project the top of the body to accurately determine the involved triangles of cells and calculate the equations of the planes only for these triangles.


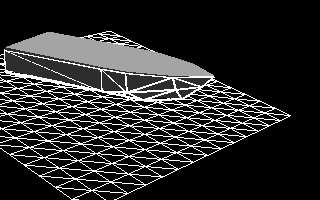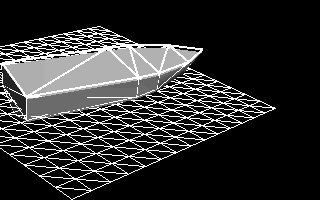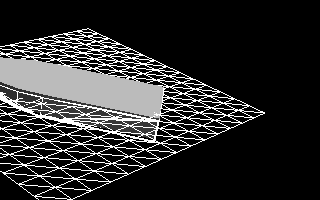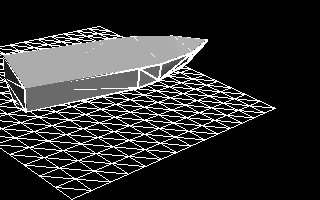
Figure 11 - Dynamic response of the vessel, on which only hydrostatic forces act on a completely flat surface of the water.

Conclusion

In this article, we present an algorithm for calculating the intersection of an arbitrary grid with the surface of water and the calculation of hydrostatic forces acting on the body described by this grid. If you wrote a program only on the basis of this algorithm, the ship would hover up and down, as if on a spring. The vessel would be pushed out of the water into the air, then fell under the influence of gravity, immersed in water and again pushed out of it. To stabilize the system, you need to add attenuation. The hydrodynamic forces described in the following article are very effective for adding damping as in the real world. But you can cheat by adding damping based on high speeds in all directions of motion, and especially in the vertical direction, so that you get a feeling of calculating hydrodynamic forces using the algorithm described above.

Notes

( *) If, for some reason, the pressure at a point of a given depth was lower relative to points at the same depth, then water at points at the same depth, subjected to greater pressure, would very quickly move to a point with less pressure and restore uniform pressure to this depth. The only thing that prevents water from elevated pressure, located at a greater depth, from rising to a depth with less pressure, is gravity; that is why there is a pressure gradient that increases with immersion.

( **) By the way, when I studied this theorem in France, it was called the Ostrogradsky theorem. Later, I learned that it is also known as the Gauss theorem. I suppose (almost as a joke) that the reason for this is that the French do not want to associate too many theorems with the Germans, and, if possible, they choose the Russian equivalent more readily. Americans tend to practicality, and to avoid long disputes, they call it simply a divergence theorem.

Appendix A. Hydrostatic forces acting on a triangle immersed in a liquid
To calculate the hydrostatic forces and moments acting on a triangle completely immersed in liquid, it is useful to divide the triangle into smaller triangles, each of which has an absolutely horizontal side. The reason for this is that it is much easier to calculate the hydrostatic forces acting on a triangle with a horizontal side: it can be divided into (practically) rectangular horizontal stripes, on whose surfaces the pressure is the same at any point.

Links

1. Simship. Edouard Halbert.
2. "Buoyancy". Joel Feldman.
3. Hydrostatic forces on a plane surface.
4. Simulating Ocean Water. Jerry Tessendorf.
5. Upper Bounds For Packing. David De Laat, Fernando Mario De Oliveira Filho, Frank Vallentin.

About the author : Jacques Kerner - Senior Software Engineer at Avalanche Studios (New York), a specialist in vehicle physics. He worked on Just Cause 3 (2015), Homefront (2011), Need for Speed: ProStreet (2007), Need for Speed: Carbon (2006) games .

The second part .