Approximation of Pi by Mandelbrot Set
I always told my friend that mathematics with its graceful abstractions has that magic power, the potential of which has not yet been fully revealed. Today I want to talk about how to approximate the number of Pi with the help of Mandelbrot set.
A few words about the set
In fact, there are a lot of articles on Habré describing the Mandelbrot set (hereinafter, the set M ), considering its properties, history and amazing beauty, supporting all this with colorful pictures. I would not like to dwell on its definition and other details, but go straight to the point. However, due to the fact that it is the central subject of this article, I will nevertheless refresh your memory.
The set M is the set of all complex numbers c , for which the function 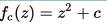 when iterating with
when iterating with  is limited. So easy.
is limited. So easy.
In practice, we apply the following theorem: if the function (above) during the iteration exceeds the value 2, then it is 100% unlimited. Therefore, you can define a lot like this:


I will not touch on the topic of visualization, we will not dig there today.
Pi?
Really, somehow?
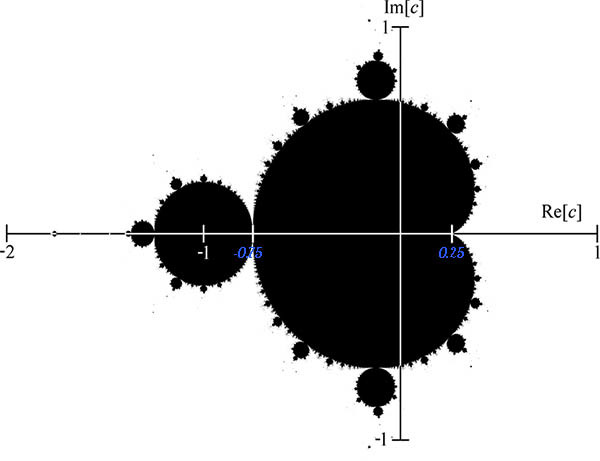
Take the "coordinate of the contact of two parts" of the set c = -0.75 + i x (where x ∈ ℚ). Let's check its belonging to the set M: let's start iterating the function  n- times from zero and check if the received value is greater than 2. If it is, then the function is diverged, and the value c does not belong to the set for a given n . Otherwise - belongs.
n- times from zero and check if the received value is greater than 2. If it is, then the function is diverged, and the value c does not belong to the set for a given n . Otherwise - belongs.
| x | c | n (number of iterations up to the function expense) |
|---|---|---|
| 0.1 | -0.75 + 0.1i | 33 |
| 0.01 | -0.75 + 0.01i | 315 |
| 0.001 | -0.75 + 0.001i | 3143 |
| 0.0001 | -0.75 + 0.0001i | 31417 |
| 0.00001 | -0.75 + 0.00001i | 314160 |
Exactly. If you put a comma in the right place, the numbers resemble the number Pi.
Probably a coincidence
We will not bother with the complex part and take the number c = 0.25. It belongs to the set with an infinitely large number of iterations. Therefore, we will "approach" this point on the right: take c = 0.26, check it; c = 0.2501, check it, etc.
| c | n (number of iterations up to the function expense) |
|---|---|
| 0.26 | thirty |
| 0.2501 | 312 |
| 0.25001 | 991 |
| 0.250001 | 3140 |
| 0.2500001 | 9933 |
| 0.25000001 | 31414 |
The sequence oscillates between two values, but the echo of pi (putting the comma in the right place) has not disappeared anywhere.
A bit of history
The set M itself, named after the mathematician Benoit Mandelbrot, is a very recent discovery. Benoit even spoke at TEDx , including about him.
In 1991, Dave Ball studied whether the "contact of two parts of a set" M is really close to c = -0.75 is infinitely thin. In the course of his research, he discovered what we are talking about.
And yet, probably a coincidence
Let us try to understand what is happening: whether we really get Pi or is it some other transcendental number.
We will do all this around point c = 0.25 (simply due to the lack of a complex part in it, it is easier).
Consider the recursive function 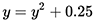 . When iterating from zero, we note that it very slowly approaches the value 0.5.
. When iterating from zero, we note that it very slowly approaches the value 0.5.

To prevent it from being "stuck" on this value, we will move this function by ε units up ( ε is infinitely small, not zero). Then she will look 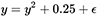 .
.
This function slowly tends to a value of 0.5, and after it passes, it quickly runs away to infinity.
We will dig further.
Let x = y + 0.5. Our task is to find a zero.
Making the replacement in the original function, we get: 
Taking as ε any small value, let's iterate the function from zero:
| y |
|---|
| 0.001 (= ε) |
| 0.002001 |
| 0.0030050040010000004 |
| 0.004014034050046026 |
| 0.005030146519400955 |
| 0.006055448893407596 |
| 0.007092117354708267 |
| 0.00814241548328122 |
| 0.009208714413183598 |
| 0.010293514834327173 |
We see that it is quite smoothly and slowly increasing near zero. Based on this, we can assume that the difference between the (n + 1) -th and n-th values of the function is close to its derivative: 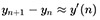 .
.
Given this, our original function will take the form: 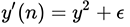 , which is the simplest differential equation of the first order. Solving it (for example, by the method of separation of variables), we get:
, which is the simplest differential equation of the first order. Solving it (for example, by the method of separation of variables), we get: 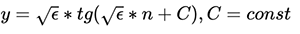
We recall our goal - the search for zero. This expression is zero only in two cases: either the square root of ε is zero — impossible by definition, or the tangent is zero. Neglecting the constant C : 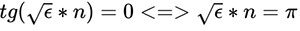 . This confirms what we saw today:
. This confirms what we saw today:
| ε | n√ε |
|---|---|
| 0.01 | 3.0 |
| 0.0001 | 3.12 |
| 0.000001 | 3.140 |
| 0.00000001 | 3.1414 |
It can be seen that the factor √ε puts the same comma in the right place.
Conclusion
Building the number of pi by this method is probably the most inefficient way: you need to do 314160 iterations in order to get 3.14160. In addition, the method does not have high accuracy due to large computation errors.
However, we managed to connect two seemingly incompatible points: the fractal and the ratio of the circumference to the length of its diameter.
')
Source: https://habr.com/ru/post/307236/
All Articles