An example of the calculation of the robust controller (H-infinity control)
What is a robust controller and why do we complicate our lives? What we do not like the standard, all recognizable, PID controller?
The answer lies in the title, with English. “Robustness” - It’s a good thing to break. In the case of a controller, this means that he must be “tough”, unyielding to changes in the control object. For example: in mat. DC motor models have 3 main parameters: resistance and inductance of the winding, and constant , which are equal to each other. To calculate the classical PID controller, look at the datasheet, take those 3 parameters and calculate the PID coefficients, everything seems to be simple, what else is needed. But the motor is a real system in which these 3 coefficients are not constant, for example as a consequence of high-frequency dynamics, which is difficult to describe or will require a high order of the system. For example : Rdatashit = 1 ohm, and in fact, R is in the interval [0.9,1.1] ohm. Thus, the quality indicators in the case of the PID controller may go beyond the given, and the robust controller takes into account uncertainties and is able to keep the quality indicators of a closed system in the required interval.
At this stage, a logical question arises: How to find this interval? It is located using the parametric identification of the model. On Habré, the OLS method was recently described ( “Parametric identification of a linear dynamical system” ), however, it gives one value of an identifiable parameter, as in a datasheet. To find the range of values, we used the “ Sparse Semidefinite Programming Relaxation of Polynomial Optimization Problems ” supplement for matlab. If it is interesting, I can write a separate article on how to use this package and how to identify.
I hope that now it has become even a little clearer why robust control is needed.
')
I will not particularly go into the theory, because I did not quite understand it; I will show the steps you need to go through to get a controller. Who cares, you can read "Essentials Of Robust Control, Kemin Zhou, John C. Doyle, Prentice Hall" or documentation Matlab.
We will use the following control system diagram:
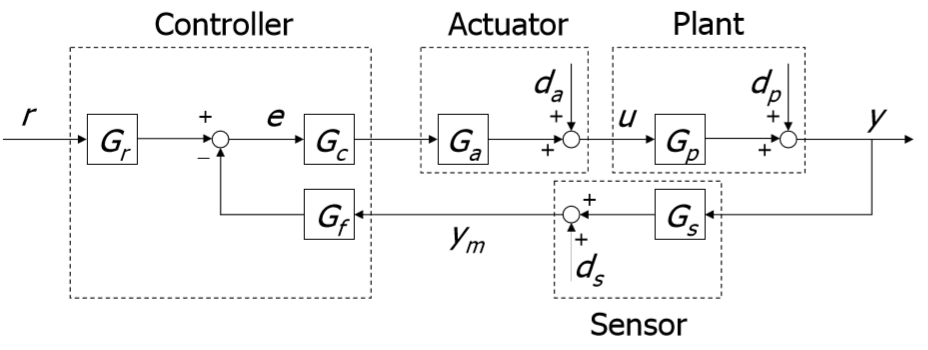
Figure 1 : Block diagram of the control system
I think everything is clear here (di - perturbations).
Formulation of the problem:
Find : Gc (s) and Gf (s) which satisfy all given conditions.
Given :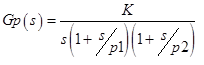 - object of management with uncertainties, which are given by intervals:
- object of management with uncertainties, which are given by intervals: 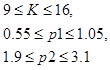
For further calculations we will use the nominal values, and we will take into account the uncertainties further.
Kn = (16 + 9) /2=12.5,p1n=0.8,p2n=2.5 , respectively, received the nominal control object:
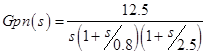
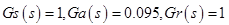
Types of disturbances:
Or in other words, these are the noise characteristics of the system elements.
I will not paint in great detail, only the main points.
One of the key steps in the H∞ method is the definition of the input and output weight functions. These weighting functions are used to normalize the input and output and reflect the time and frequency dependences of the input disturbances and the operating characteristics of the output variables (errors) [1]. Honestly, this means almost nothing to me, especially if you come across this method for the first time. In a nutshell, the weight functions are used to set the desired properties of the control system. For example, in the feedback there is a sensor that has noise, usually high-frequency, and so, the weight function will be a sort of boundary that the controller should not cross to filter out the sensor noise.
Below we will derive these weight functions based on performance.
As a result, we get:
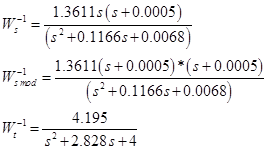
The Hinf method or the method of minimizing the infinite norm of Hinfinity refers to the general formulation of a control problem which is based on the following scheme of the control system with feedback:
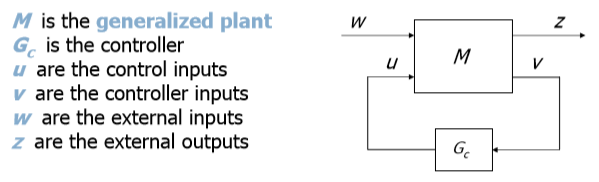
Figure 12 : Generalized control system diagram
Let us go to the point of calculation of the controller and what is needed for this. The study of the calculation algorithms was not explained to us, they said: “Do it like this and everything will turn out”, but the principle is quite logical. The controller is obtained during the solution of the optimization problem:
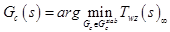
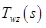 - closed transfer function from W to Z.
- closed transfer function from W to Z.
Now we need to make a generalized plant (dotted rectangle of rice below). We have already determined gpn, it is a nominal control object. Gc - the controller that we get in the end. W1 = Ws (s), W2 = max (WT (s), Wu (s)) are weight functions defined earlier. Wu (s) is a weight function of uncertainty, let's define it.

Figure 13 : Expanded control scheme
Suppose that we have multiplicative uncertainties in the control object, we can depict it like this:
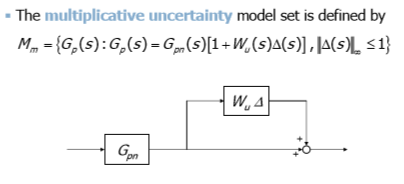
Figure 14 : Multiplicative uncertainty
And so for finding Wu we use matlab. We need to build a Bode with all possible deviations from the nominal control object, and then build a transfer function that describes all these uncertainties:

Let's make about 4 passes for each parameter and build a bode. As a result, we get this:
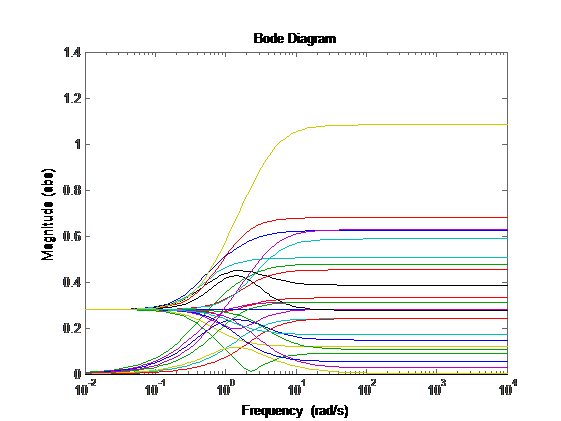
Figure 15 : Uncertainty Bode Digram
Wu will lie above these lines. In the matlab there is a tool that allows the mouse to specify points and builds the transfer function using these points.
After the introduction of points, the curve grows old and it is proposed to introduce the degree of transfer function, we introduce degree 2.
Here's what happened:
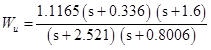
Now we define W2, for this we construct Wt and Wu:
From the graph you can see that Wt is more than Wu means W2 = Wt.
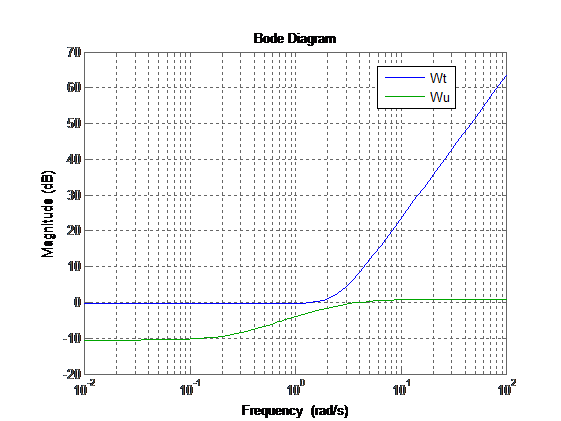
Figure 16 : Definition W2
Next, we need to build a generalized plant in the simulator as done below:
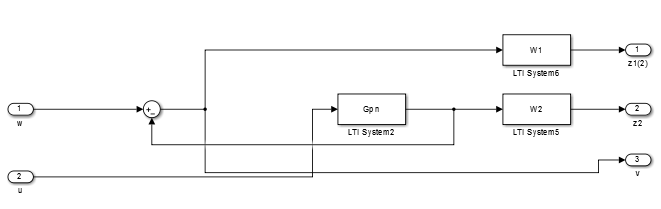
Figure 17 : Block diagram of the Generalized plant in simulink
And save as a name, for example g_plant.mdl
One important point:
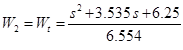 - not proper tf, if we leave it so it will give us an error. For this we replace
- not proper tf, if we leave it so it will give us an error. For this we replace 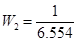 and then add two zeros to the z2 output using “sderiv“.
and then add two zeros to the z2 output using “sderiv“.
After executing this code, we get the controller:
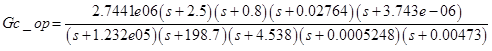
In principle, it is possible to leave it that way, but usually low and high frequency zeros and poles are removed. Thus, we reduce the controller order. And we get the following controller:
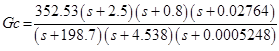
let's get this Hichols chart:
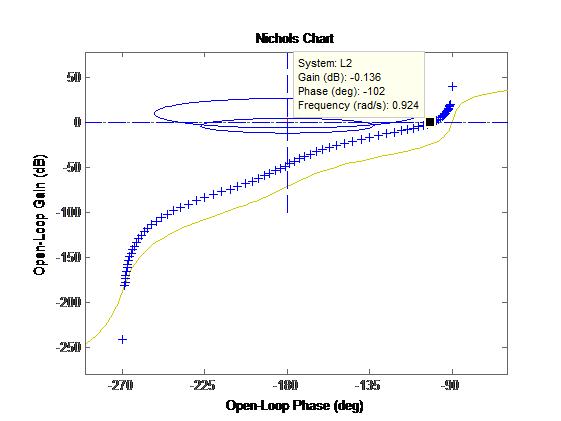
Figure 18 : Hichols chart of open-loop system with received controller
And Step response:

Figure 19 : Transient response of a closed system with a controller
And now the sweetest. Was our controller robust or not? For this experiment, we just need to change our control object (coefficients k, p1, p2) and see the step response and characteristics of interest, in our case this is overshoot, control time for 5% and rise time [2].

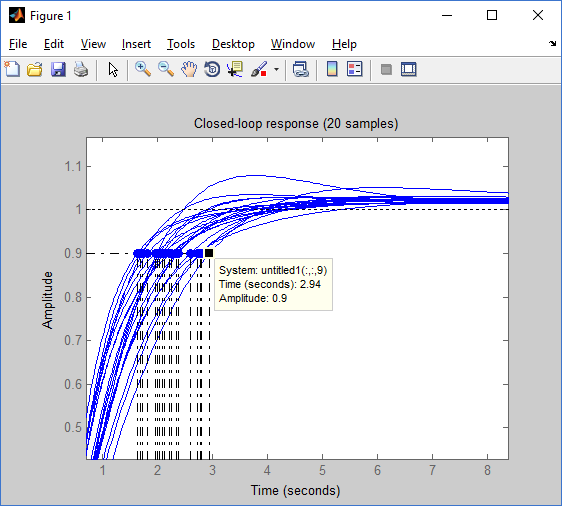
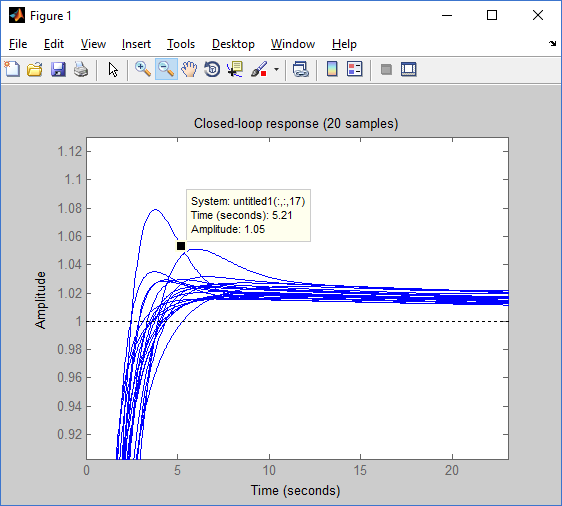
Figure 20 : Time characteristics for different parameters of the control object
Having built 20 different transient characteristics, I selected the maximum values for each time characteristic:
• Maximum re-regulation - 7.89%
• Max rise time - 2.94 s
• Max time of a regelirovaniye of 5% - 5.21 sec.
And about a miracle, the characteristics where necessary not only for the nominal object, but also for the interval of parameters.
And now we compare with the classic PID controller, and see if the game was worth the candle or not.
PID calculated pidtool for the nominal control object (see above):
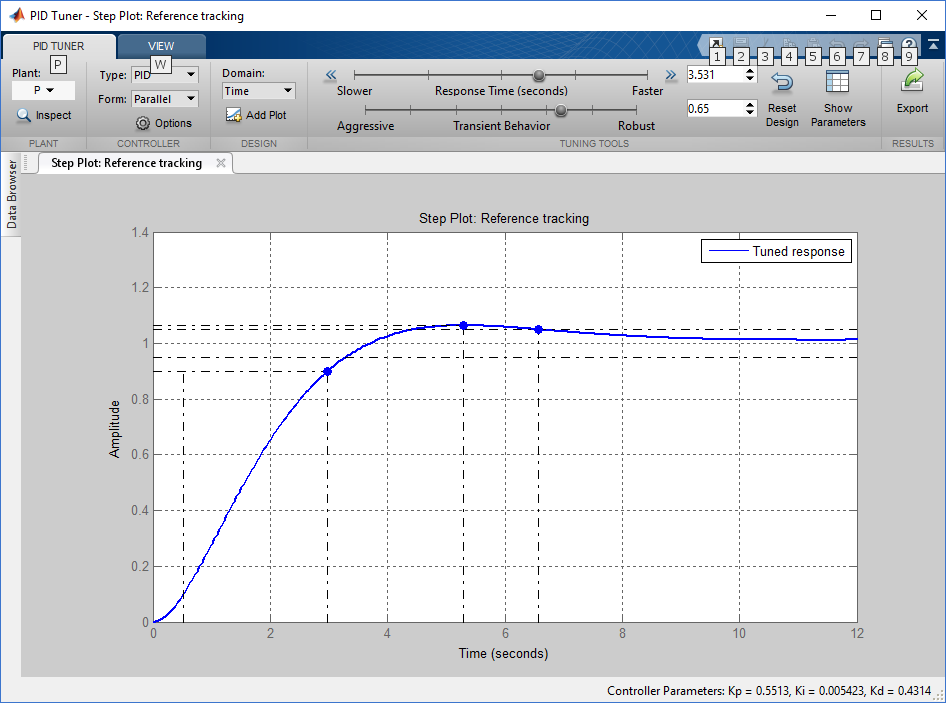
Figure 21 : Pidtool
We get this controller:
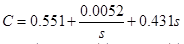
Now H-infinity vs PID :

Figure 22 : H-infinity vs PID
It can be seen that the PID does not cope with such uncertainties and the HRP goes beyond the specified limits, while the robust controller "rigidly" keeps the system at specified reregulation intervals, rise time and regulation.
In order not to lengthen the article and not to bore the reader, I will omit the verification of characteristics 2-5 (errors), I will say that in the case of a robust controller all errors are lower than specified, a test was also performed with other parameters of the object:

Errors were lower than the specified ones, which means that the controller completely copes with the task. While PID failed only with point 4 (dp error).
That's all for the calculation of the controller. Criticize, ask.
Link to file: drive.google.com/open?id=0B2bwDQSqccAZTWFhN3kxcy1SY0E
1. Guidelines for the Selection of Weighting Functions for H-Infinity Control
2. it.mathworks.com/help/robust/examples/robustness-of-servo-controller-for-dc-motor.html
The answer lies in the title, with English. “Robustness” - It’s a good thing to break. In the case of a controller, this means that he must be “tough”, unyielding to changes in the control object. For example: in mat. DC motor models have 3 main parameters: resistance and inductance of the winding, and constant , which are equal to each other. To calculate the classical PID controller, look at the datasheet, take those 3 parameters and calculate the PID coefficients, everything seems to be simple, what else is needed. But the motor is a real system in which these 3 coefficients are not constant, for example as a consequence of high-frequency dynamics, which is difficult to describe or will require a high order of the system. For example : Rdatashit = 1 ohm, and in fact, R is in the interval [0.9,1.1] ohm. Thus, the quality indicators in the case of the PID controller may go beyond the given, and the robust controller takes into account uncertainties and is able to keep the quality indicators of a closed system in the required interval.
At this stage, a logical question arises: How to find this interval? It is located using the parametric identification of the model. On Habré, the OLS method was recently described ( “Parametric identification of a linear dynamical system” ), however, it gives one value of an identifiable parameter, as in a datasheet. To find the range of values, we used the “ Sparse Semidefinite Programming Relaxation of Polynomial Optimization Problems ” supplement for matlab. If it is interesting, I can write a separate article on how to use this package and how to identify.
I hope that now it has become even a little clearer why robust control is needed.
')
I will not particularly go into the theory, because I did not quite understand it; I will show the steps you need to go through to get a controller. Who cares, you can read "Essentials Of Robust Control, Kemin Zhou, John C. Doyle, Prentice Hall" or documentation Matlab.
We will use the following control system diagram:

Figure 1 : Block diagram of the control system
I think everything is clear here (di - perturbations).
Formulation of the problem:
Find : Gc (s) and Gf (s) which satisfy all given conditions.
Given :
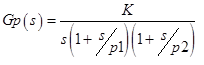 - object of management with uncertainties, which are given by intervals:
- object of management with uncertainties, which are given by intervals: 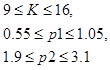
For further calculations we will use the nominal values, and we will take into account the uncertainties further.
Kn = (16 + 9) /2=12.5,p1n=0.8,p2n=2.5 , respectively, received the nominal control object:
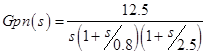
Types of disturbances:
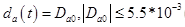 - step perturbations of the amplifier with amplitude D_a0
- step perturbations of the amplifier with amplitude D_a0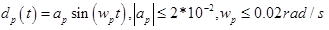 - sinusoidal disturbance of the control object with amplitude a_p and frequency w_p
- sinusoidal disturbance of the control object with amplitude a_p and frequency w_p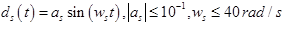 - sinusoidal disturbances of the sensor with amplitude a_s and frequency w_s
- sinusoidal disturbances of the sensor with amplitude a_s and frequency w_s
Or in other words, these are the noise characteristics of the system elements.
Performance specifications
- Gain control system Kd = 1
- The steady-state error when the input effects Ramp R0 = 1:
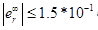
- A fixed error in the presence of da:
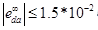
- Fixed error in the presence of dp:

- Fixed error in the presence of ds:

- Overshoot
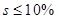
- Regulation time
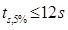
- Rise time
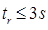
Decision
I will not paint in great detail, only the main points.
One of the key steps in the H∞ method is the definition of the input and output weight functions. These weighting functions are used to normalize the input and output and reflect the time and frequency dependences of the input disturbances and the operating characteristics of the output variables (errors) [1]. Honestly, this means almost nothing to me, especially if you come across this method for the first time. In a nutshell, the weight functions are used to set the desired properties of the control system. For example, in the feedback there is a sensor that has noise, usually high-frequency, and so, the weight function will be a sort of boundary that the controller should not cross to filter out the sensor noise.
Below we will derive these weight functions based on performance.
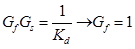 Everything is simple here
Everything is simple here- In this paragraph, we need to determine how many poles in zero it is necessary to have for the controller (denoted by µ) to satisfy Condition 2. To do this, we use the table:
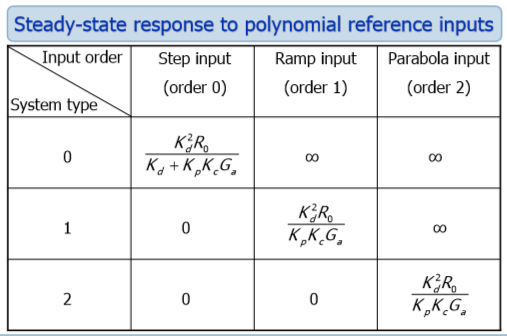
Figure 2 : Position, Speed, and Acceleration Errors
System type or astatism (p) - denotes the number of poles at zero, the control object, in our case p = 1 (a system with first-order astatism). Since our control object is a system with astatism of the first order, in this case the controller should not have poles at zero. We use the formula:
μ + p = h
Where h is the input signal order, for ramp h = 1;
μ = hp = 1-1 = 0
Now we use the finite value theorem to find e_r∞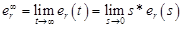
Where e_r is the tracking error,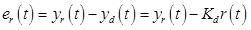
yr is the actual output (see Figure 1), yd is the desired output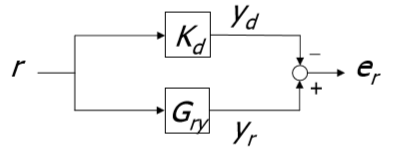
Figure 3 : Tracking Error Detection
As a result, we get this: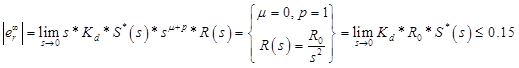
This is a steady-state error formula, unknown in this equation S (Sensitivity function)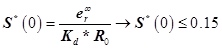
Where - sensitivity function, L (s) - loop function. Without a clue how they are translated into Russian, leave English names. Also complementary sensitivity function
- sensitivity function, L (s) - loop function. Without a clue how they are translated into Russian, leave English names. Also complementary sensitivity function  (As can be seen from the formulas, S and T includes Gc - a calculated controller, we find the limits for S and T from errors and performance, respectively, we define the weight functions from S and T, and the matlab from the weight functions find the desired controller.)
(As can be seen from the formulas, S and T includes Gc - a calculated controller, we find the limits for S and T from errors and performance, respectively, we define the weight functions from S and T, and the matlab from the weight functions find the desired controller.)
In a nutshell about S and T [1].- The sensitivity function , S (s), describes the output y (s) as a function of the disturbance da and dp, also relates the tracking error and the input effect (for low frequencies)
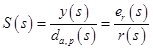
- Complementary sensitivity function , T (s), connects the output of the system with the input action, and also shows how much sensor noise ds affects the output of the system (for high frequencies).

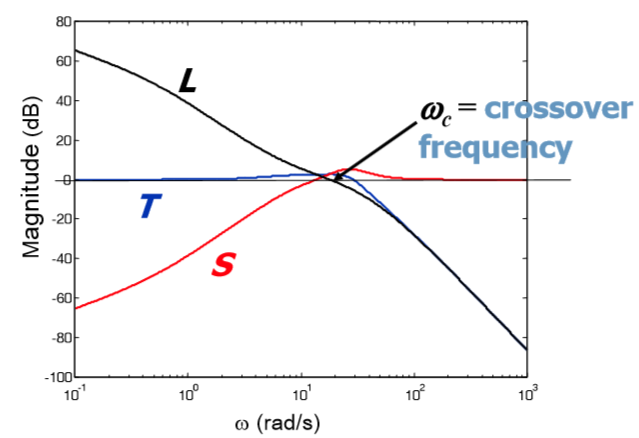
Figure 4 : Bode diagram for S, T and L
From the graph it is clear that S weakens low-frequency disturbances, while T weakens high-frequency disturbances. - The sensitivity function , S (s), describes the output y (s) as a function of the disturbance da and dp, also relates the tracking error and the input effect (for low frequencies)
- We use the finite value theorem for e_da
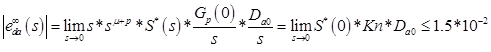

Since we have two inequalities, we find a condition that satisfies both: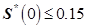
This condition says where the Sensitivity function should cross the 0 dB axis in the Bode diagram.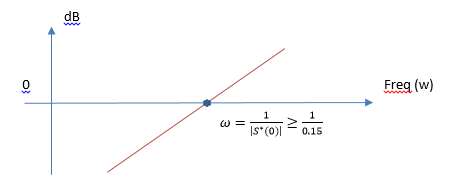
Figure 5 : Bode for S - Dp we have a harmonic disturbance, low frequency. Create a mask for S in the frequency range wp

This value indicates that S must be below -32 dB for wp frequencies in order to filter out disturbances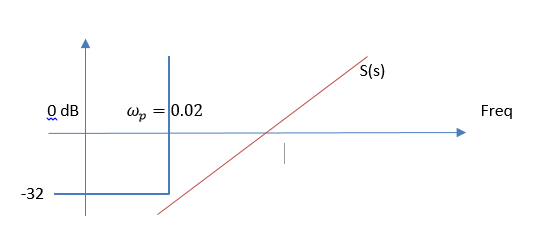
Figure 6 : Mask for S - Ds is also a high-frequency harmonic perturbation, here T will play its role
Do the same: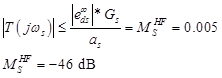
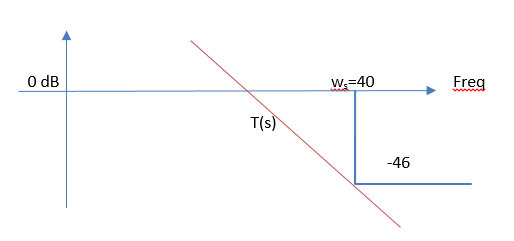
Figure 7 : Mask for T
The complex order of the weight functions is determined from the condition of the mask and the frequency of intersection with the 0 axis. In our cases from wp to w is about one decade, and since we have -32 dB, then S must be at least 2 orders of magnitude. The same goes for T.
As a result, the constraints schematically have the following form for S and T, respectively: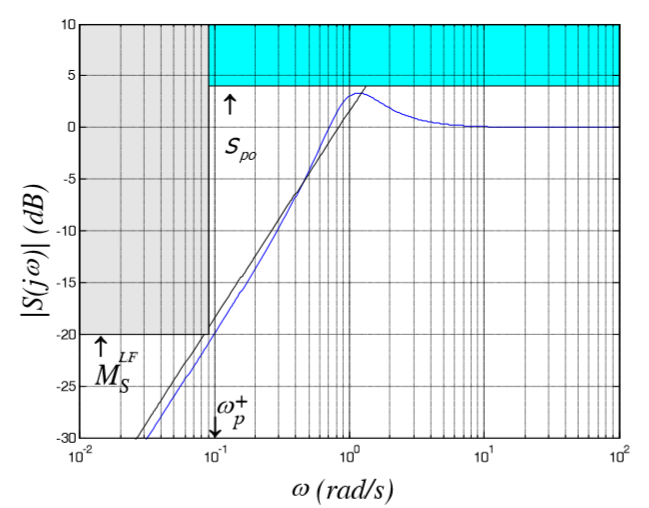
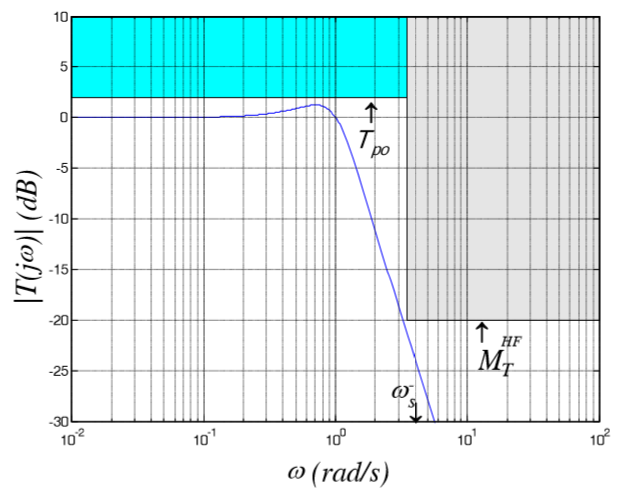
Figure 8 : All masks for S and T - To translate the time characteristics we use the graphs.
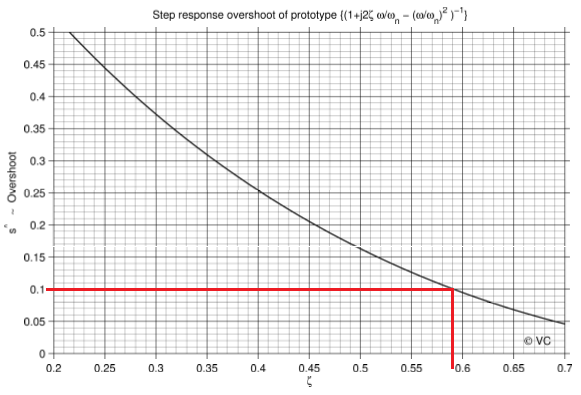
Figure 9 : Graph of damping coefficient versus re-adjustment
Knowing the re-adjustment we find the coefficient of damping for 10% ->
ξ = 0.59
Knowing the damping coefficient, we find the (resonant) maximum allowable value for S and T
Figure 10 : Graph of S_p0 and T_p0 vs. Damping Factor
S_p0 = 1.35
T_p0 = 1.05 - From the time of regulation and tuning we find how fast the control system should be

Next, we find the natural frequency for S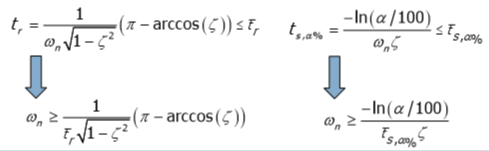
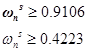
The natural frequency for T is found in the Bode diagram. According to condition 5, the frequency 40 rad / s T should be below -46 dB, which means that when tilted at -40 dB / dec, the natural frequency should be below 4 rad / s. Building the Bode, we select the optimal value, I got that: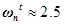
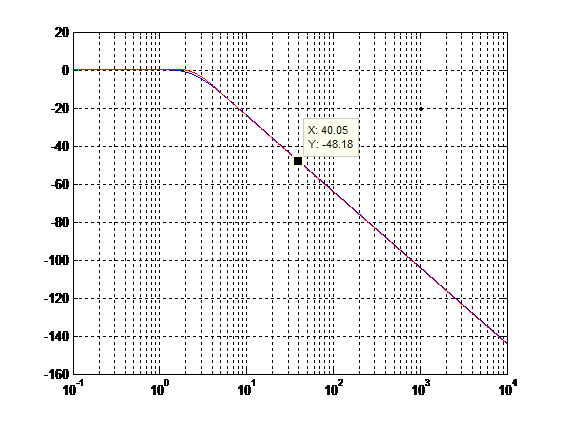
Figure 11 : T-function bode
After that, we have all the data to build ST, which we then transform into weight functions. ST have the following form: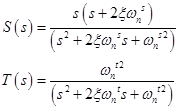
Usually, Butterworth coefficients are used to build weight functions.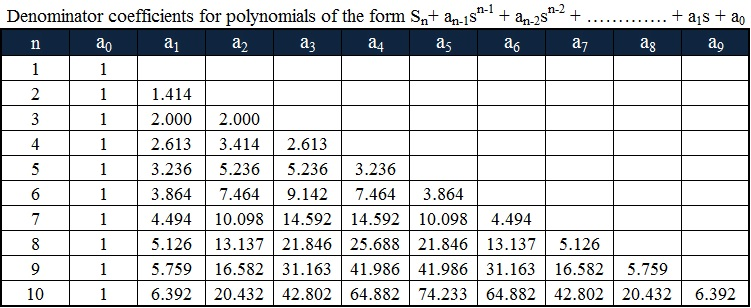
Weight functions are: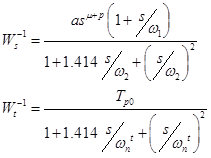
For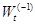 everything is simple, and we have everything we need to substitute in the formula. For
everything is simple, and we have everything we need to substitute in the formula. For 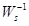 need a few more calculations.
need a few more calculations.
Since the performance characteristics give us the boundary conditions under which our controller will fulfill all the conditions. Weight functions unite all the conditions in themselves and then are used as the right and left border in which to be the controller satisfying all the conditions.
For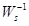
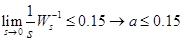 this parameter is called generalized DC gain, it displays the behavior for low frequencies (s = 0)
this parameter is called generalized DC gain, it displays the behavior for low frequencies (s = 0)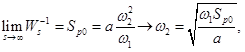 , w1 choose approximately near the frequency of the disturbance or one decade lower (set at 0.0005 rad / s)
, w1 choose approximately near the frequency of the disturbance or one decade lower (set at 0.0005 rad / s)- • LMI solver does not accept function zeroes (zero in origine), therefore s is replaced by zero near the origin (s + 0.0005)
As a result, we get:
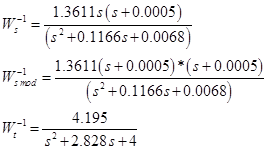
Generalized plant
The Hinf method or the method of minimizing the infinite norm of Hinfinity refers to the general formulation of a control problem which is based on the following scheme of the control system with feedback:

Figure 12 : Generalized control system diagram
Let us go to the point of calculation of the controller and what is needed for this. The study of the calculation algorithms was not explained to us, they said: “Do it like this and everything will turn out”, but the principle is quite logical. The controller is obtained during the solution of the optimization problem:
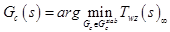
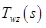 - closed transfer function from W to Z.
- closed transfer function from W to Z.Now we need to make a generalized plant (dotted rectangle of rice below). We have already determined gpn, it is a nominal control object. Gc - the controller that we get in the end. W1 = Ws (s), W2 = max (WT (s), Wu (s)) are weight functions defined earlier. Wu (s) is a weight function of uncertainty, let's define it.

Figure 13 : Expanded control scheme
Wu (s)
Suppose that we have multiplicative uncertainties in the control object, we can depict it like this:

Figure 14 : Multiplicative uncertainty
And so for finding Wu we use matlab. We need to build a Bode with all possible deviations from the nominal control object, and then build a transfer function that describes all these uncertainties:

Let's make about 4 passes for each parameter and build a bode. As a result, we get this:

Figure 15 : Uncertainty Bode Digram
Wu will lie above these lines. In the matlab there is a tool that allows the mouse to specify points and builds the transfer function using these points.
Code
mf = ginput (20);
magg = vpck (mf (:, 2), mf (:, 1));
Wa = fitmag (magg);
[A, B, C, D] = unpck (Wa);
[Z, P, K] = ss2zp (A, B, C, D);
Wu = zpk (Z, P, K)
magg = vpck (mf (:, 2), mf (:, 1));
Wa = fitmag (magg);
[A, B, C, D] = unpck (Wa);
[Z, P, K] = ss2zp (A, B, C, D);
Wu = zpk (Z, P, K)
After the introduction of points, the curve grows old and it is proposed to introduce the degree of transfer function, we introduce degree 2.
Here's what happened:
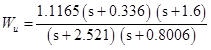
Now we define W2, for this we construct Wt and Wu:
From the graph you can see that Wt is more than Wu means W2 = Wt.

Figure 16 : Definition W2
Next, we need to build a generalized plant in the simulator as done below:

Figure 17 : Block diagram of the Generalized plant in simulink
And save as a name, for example g_plant.mdl
One important point:
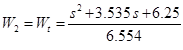 - not proper tf, if we leave it so it will give us an error. For this we replace
- not proper tf, if we leave it so it will give us an error. For this we replace 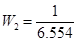 and then add two zeros to the z2 output using “sderiv“.
and then add two zeros to the z2 output using “sderiv“.Implementation in matab
p = 2; % frequency of zeros in the frequency T function
[Am, Bm, Cm, Dm] = linmod ('g_plant');
M = ltisys (Am, Bm, Cm, Dm);
M = sderiv (M, 2, [1 / p 1]);
M = sderiv (M, 2, [1 / p 1]);
[gopt, Gcmod] = hinflmi (M, [1 1], 0.0.01, [0.0.0]);
[Ac, Bc, Cc, Dc] = ltiss (Gcmod);
[Gc_z, Gc_p, Gc_k] = ss2zp (Ac, Bc, Cc, Dc);
Gc_op = zpk (Gc_z, Gc_p, Gc_k)
[Am, Bm, Cm, Dm] = linmod ('g_plant');
M = ltisys (Am, Bm, Cm, Dm);
M = sderiv (M, 2, [1 / p 1]);
M = sderiv (M, 2, [1 / p 1]);
[gopt, Gcmod] = hinflmi (M, [1 1], 0.0.01, [0.0.0]);
[Ac, Bc, Cc, Dc] = ltiss (Gcmod);
[Gc_z, Gc_p, Gc_k] = ss2zp (Ac, Bc, Cc, Dc);
Gc_op = zpk (Gc_z, Gc_p, Gc_k)
After executing this code, we get the controller:
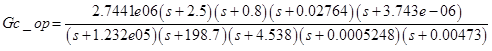
In principle, it is possible to leave it that way, but usually low and high frequency zeros and poles are removed. Thus, we reduce the controller order. And we get the following controller:
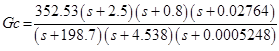
let's get this Hichols chart:

Figure 18 : Hichols chart of open-loop system with received controller
And Step response:

Figure 19 : Transient response of a closed system with a controller
And now the sweetest. Was our controller robust or not? For this experiment, we just need to change our control object (coefficients k, p1, p2) and see the step response and characteristics of interest, in our case this is overshoot, control time for 5% and rise time [2].



Figure 20 : Time characteristics for different parameters of the control object
Having built 20 different transient characteristics, I selected the maximum values for each time characteristic:
• Maximum re-regulation - 7.89%
• Max rise time - 2.94 s
• Max time of a regelirovaniye of 5% - 5.21 sec.
And about a miracle, the characteristics where necessary not only for the nominal object, but also for the interval of parameters.
And now we compare with the classic PID controller, and see if the game was worth the candle or not.
PID calculated pidtool for the nominal control object (see above):

Figure 21 : Pidtool
We get this controller:
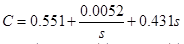
Now H-infinity vs PID :

Figure 22 : H-infinity vs PID
It can be seen that the PID does not cope with such uncertainties and the HRP goes beyond the specified limits, while the robust controller "rigidly" keeps the system at specified reregulation intervals, rise time and regulation.
In order not to lengthen the article and not to bore the reader, I will omit the verification of characteristics 2-5 (errors), I will say that in the case of a robust controller all errors are lower than specified, a test was also performed with other parameters of the object:

Errors were lower than the specified ones, which means that the controller completely copes with the task. While PID failed only with point 4 (dp error).
That's all for the calculation of the controller. Criticize, ask.
Link to file: drive.google.com/open?id=0B2bwDQSqccAZTWFhN3kxcy1SY0E
Bibliography
1. Guidelines for the Selection of Weighting Functions for H-Infinity Control
2. it.mathworks.com/help/robust/examples/robustness-of-servo-controller-for-dc-motor.html
Source: https://habr.com/ru/post/306934/
All Articles