Shannon Communications Model (translation of Great Principles of Computing)

Translation of Great Principles of Computing

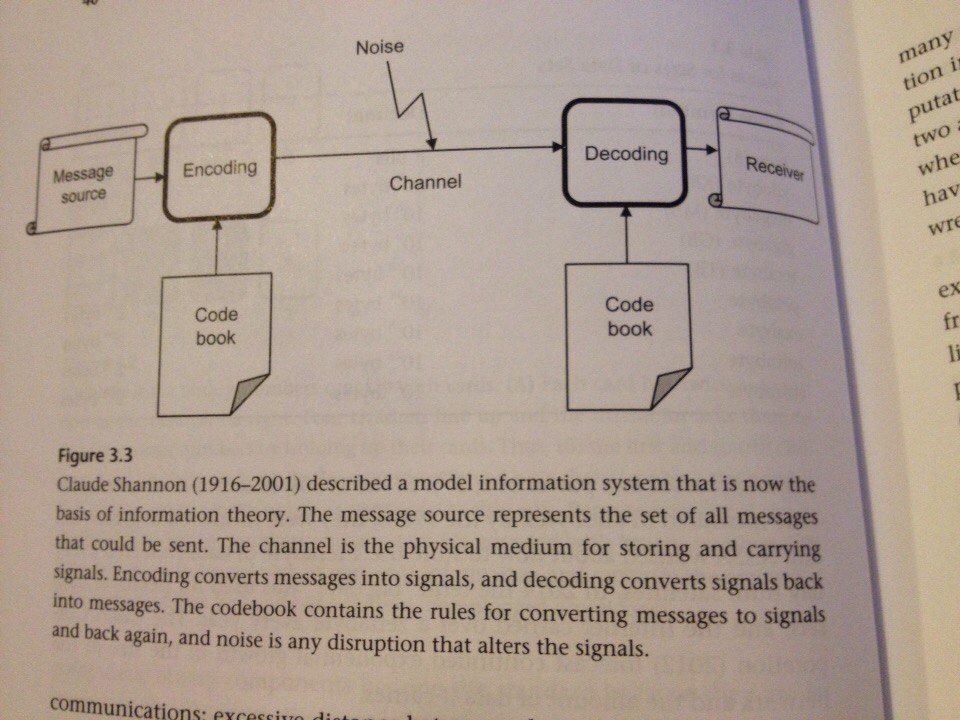
In 1948, Shannon in his "theory of communication" proposed a mathematical model of communication. Its meaning is as follows.
')


There is a source and there is a receiver. The source sends messages, and the receiver accepts. Both participants use the same vocabulary for encoding and decoding messages.
The Shannon model is applicable to any system that encodes, decodes, transmits, stores and receives messages. Thus, nature can be considered as a source of physical laws (messages), and the process of discovering these laws as a channel of communication (Dretske 1981).

Noise is another component of this model. Noise is what causes the receiver to misinterpret messages. Poor visibility (fog and twilight) disrupts semaphore communication between ships; lightning flashes interrupt the transmission of AM radio waves; scratches on a CD can make it unreadable; a lot of extraneous noise make speech unintelligible.

It is worth noting that coding in communication systems is not the same as encrypting secret messages. Encryption assumes the existence of a special key: only the one who has this key can receive the source code.

In his model, Shannon chose bits as the “coding dictionary”. He argued that any message can be represented as a set of bits, i.e. literally digitized, any information turns into numbers, into a set of zeros and ones.

It is interesting to look at how to digitize messages and what noise is in a simplified example.
Let the source can only transmit messages consisting of 4 letters: A, B, C and D. Use two-bit codes to designate these letters:

A: 11
B: 10
C: 01
D: 00

For example, the source wants to say: "CAB". This message corresponds to the code "011110". The source sends this set of bits to the channel, and the receiver receives them and starts the reverse process: breaks the code into pairs of bits and compares it with the dictionary.

The question arises: are two bits enough to encode these letters? Naturally, the less bits are required for this purpose - the better: messages take up less space, are transmitted faster. However, the short code is much easier to spoil, making even a small distortion, which introduces noise.

For example, if the first bit in the letter A is lost for some reason, we get 010110 - which corresponds to CCB, and this completely changes the meaning of the message. How to be?

Add an extra bit for each letter (parity bit):

A: 110
B: 101
C: 011
D: 000

Now, if the first bit in A is lost, we get 010 - there is no such triple in the dictionary, so the receiver can easily understand that this is a mistake. However, he will not be able to recover the original message.

If you add a few extra bits, it will help the receiver not only to find out where the error is, but also to restore the source code:

A: 11111
B: 10010
C: 01001
D: 00100

Each code differs from the other by at least 3 bits. Now the broken bit shows a set that still differs from the correct one by one bit, but now it differs by two or more bits from all the others in the dictionary! Accordingly, the receiver can easily “correct” the corrupted message.

Communication Infern Richard Hemming (Richard Hamming) first formulated a rule by which a sufficient “distance” between sets of bits can be determined. According to Hamming, distance is the number of bits for which sets of bits differ from each other. Now this value is called Hamming distance.

Hamming realized that in order to correct the k errors, it is enough that the Hamming distance was 2 ^ k - 1. Hamming also developed a family of codes (Hamming codes), which are obtained by adding parity bits to the source codes and creating circuits that make it easy receive original messages (subject to correction of errors). Hamming codes are widely used when transferring messages from the processor to the computer's memory.

Hamming codes work well when noise is randomly distributed. However, in some signals, noise occurs periodically or for a relatively long time. Another type of code, Reed-Solomon codes, does a good job with this task. From the point of view of mathematics, they are more cunning, however, both can easily be performed on integrated circuits of a computer.