Implementation of the Bailey — Borwein — Plaff algorithm on Golang

_{Pi number, I tell you, brothers,
It's easier to memorize.
Three fourteen fifteen
Nine two, six five, three five.
© Dmitry Eight}

Recently, I needed the number of pi in hexadecimal format. Approximately 10,000 decimal places. However, all publications in the network usually show Pi in decimal form. Stumbling a bit, I found Pi in binary form, and it more than suited me: a simple conversion solved the tasks. There would end the story, but as they say, "a spoon was found, but the sediment remained." Below you can see a simple implementation of the PiHex library, which generates a digit, or a sequence of digits in any position after the decimal point of Pi (though not more than 10,000,000).

So, there is an "BBP" algorithm, which allows you to calculate in hexadecimal Pi the sign in any position after the comma. This algorithm itself is from the category of “Kranikovykh”, more details about this family of algorithms can be found in the article: “Kranik”, or an algorithm for finding digits of the number Pi . On the implementation of the "BBP" algorithm in the C language, there was also an article in Habré: Calculating the Nth sign of Pi without calculating the previous ones

About the algorithm

The description of the algorithm is best read in the article “The BBP Algorithm for Pi”, published by David Bailey on September 17, 2006: www.davidhbailey.com/dhbpapers/bbp-alg.pdf By the way, it is written quite understandably, at least not a mathematician also can understand something. From the article it is clear that for the calculation is used not very complex formula in the form:

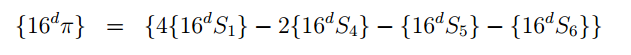
while S _{j is} calculated as:

the result is a slightly more bulky formula

')

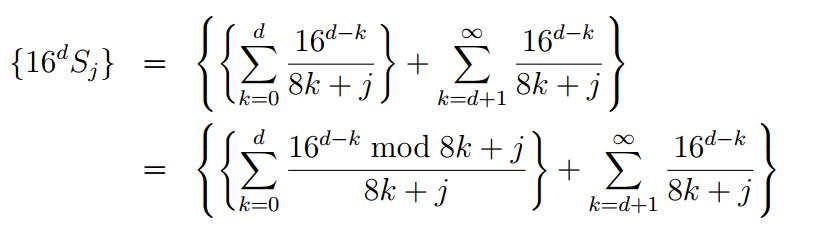
Implementation

When migrating to Go, implementation was implemented using gorutin to parallelize resource-intensive computations S _j . This made it possible to significantly speed up computations, since on modern computers there are usually more cores in the processor than one. However, it is possible that this is not strong and is needed if one sign is required, but if it is a thousand, the speed of work will be important in any case.

API

Using the library is not easy, but very easy, because in fact, it only supports one method. The example below shows how to connect the library and get the first 20 decimal places:

package main import ( "fmt" "github.com/claygod/PiHex" ) func main() { pi := PiHex.New() fmt.Print("The first 20 digits of Pi (hexadecimal): ", pi.Get(0, 20)) } 

Where is the PiHex library useful?

Actually, there, where you need Pi, and at the same time it is in hexadecimal form. If large orders are required, then it may be worthwhile to calculate Pi in advance and / or use the already calculated results, since for example, on my computer, the calculation of ten characters after the 1,000,000 position took a little more than ten seconds. Due to the limit of 10,000,000 decimal places, the PiHex library is in no way suitable for setting new records in Pi computation.

Configuration

In fact, only one parameter can be changed: STEP. It indicates how many digits can be calculated per iteration. The default is 9, and this is the maximum possible number that allows you to maintain the correctness of the calculated result. If in doubt, the figure can be reduced, which is true, will reduce the speed of the library.

Testing

Since the library API is more than simple, I hope I was able to cover all possible holes in the library in the tests. And yes, when I wrote the tests, the holes were found, it could not have done without it.

Links

PiHex Library on Github
Formula Bailey - Borwein - Plaffa
David Bailey article on the BBP algorithm