Who was Ramanujan?

Translation of Stephen Wolfram's post " Who Was Ramanujan? ".
I express my deep gratitude to Polina Sologub for assistance in translating and preparing the publication.

---

Content

Amazing letter
Beginning of the story
Who was hardy?
The letter and its consequences
Ramanujan Work Style
See what's important
Truth or explanation
Going to Cambridge
Ramanujan at Cambridge
What happened next
What happened to Hardy?
Ramanujan Math
Facts - random or not?
Ramanujan Works Automation
Modern Ramanujana?
What would happen if Ramanujan had Mathematica?

---

This week came the film "The Man Who Cognized Infinity " (which was shown to me last fall by Mandjul Bhargava and Ken Ono ), so I could not help writing about his main character, Srinivas Ramanujana.

Amazing letter

Previously, they came by regular mail. Now - by e-mail. For years, letters from all over the world have flocked to me, which contain bold statements about primes, the theory of relativity, artificial intelligence, consciousness, and many other things. Looking at these messages, I recall the story of Ramanujan and invariably postpone my ideas and projects in order to at least see them.
')
Around January 31, 1913, a mathematician named Hardy from Cambridge, England received a package of documents with a cover letter that began: " Dear sir, I want to introduce myself: I am a clerk from the port accounting in Madras with a salary of £ 20 a year. I am 23 years old .... "And he continued: he wrote that he had made" amazing "progress in the theory of divergent series in mathematics and solved the long-standing problem of the distribution of prime numbers . The cover letter ended with the words:" I am poor; if you decide that there is something valuable here, I would like my theorems to be published ... I am inexperienced, and any of your advice is valuable to me. I apologize for the inconvenience. Yours sincerely, Yours, S. Ramanujan . "

This was followed by at least 11 pages of technical results from a number of areas of mathematics (of which 2 are lost). There was an absurd at first glance statement that the sum of all positive numbers is -1/12 :





There were statements suggesting the use of a kind of experimental approach in mathematics:



There were more exotic pages with formulas like this:



What is it? Where did they come from? Are they right?

The concepts themselves must be well known to the person who has studied mathematics in college. However, it was not just difficult college level exercises that were attached to the letter. If you look closely, something completely unusual and unexpected happens on every page of the letter — it seems to be a math of a different level.

Today, we can use Mathematica or Wolfram | Alpha . And sometimes we can even just enter a question and immediately get an answer:



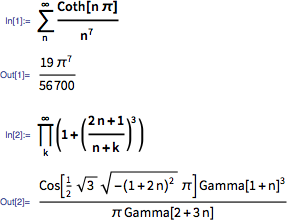
It can be verified (as was G. H. Hardy in 1913) that the formulas are correct. However, what kind of person could get them out? And How? Are they part of a larger picture or, in a sense, just random random facts from mathematics?

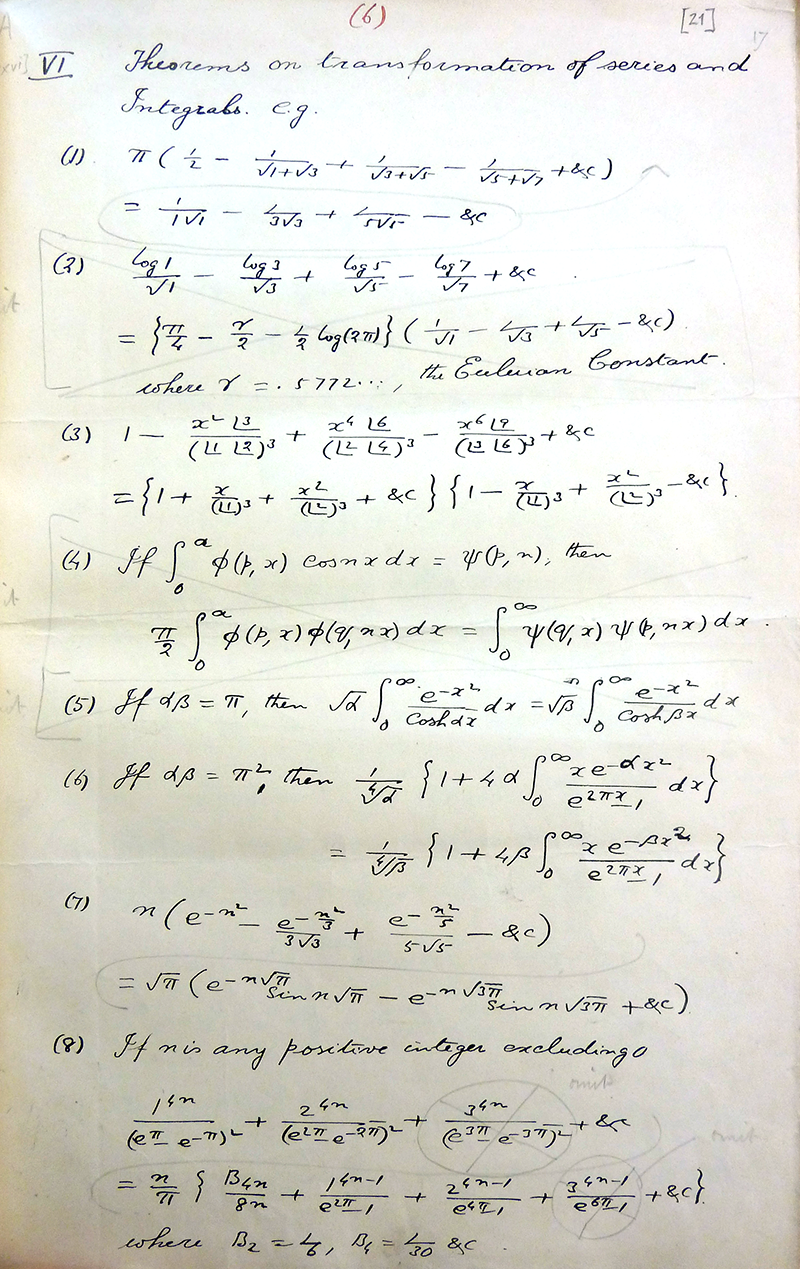
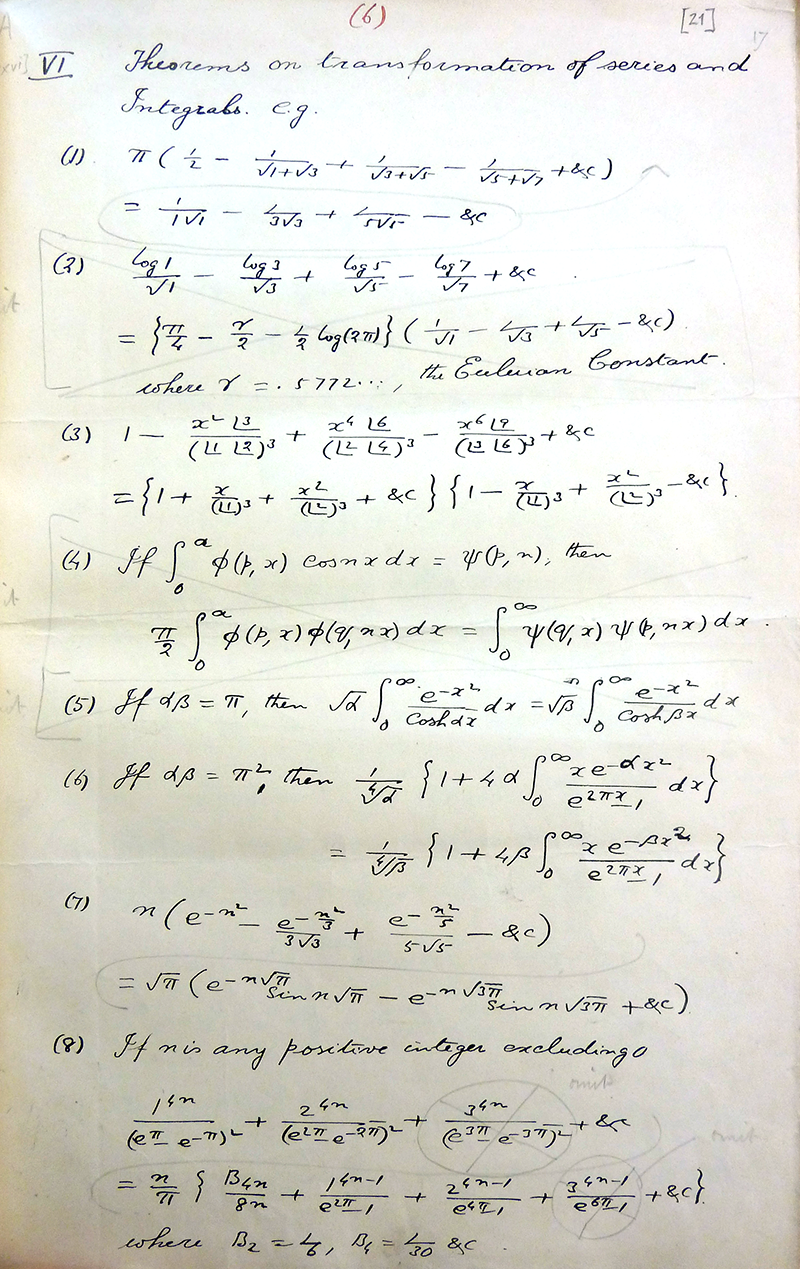
Beginning of the story

Behind this letter stands the remarkable story of Ramanujan .

He was born in a small town in India on December 22, 1887 (this means that he was not “about 23” years old when he wrote his letter to Hardy, but all 25 ). His family was poor and belonged to the caste of Brahmins (priests, teachers, etc.). Already at the age of 10, Ramanujan clearly stood out among others on the basis of examinations in the renewed school system. He was also known for his exceptional memory: he could recite pi numbers as well as the roots of Sanskrit words. When he graduated from high school at the age of 17, he was given a scholarship to attend college.

In high school, Ramanujan began to independently study mathematics and conduct his own research on the numerical evaluation of Euler's constant and properties of Bernoulli numbers . He was lucky that at the age of 16 (in those days, long before the Internet!), He received a copy of surprisingly good and complete (at least as of 1886) math summaries for high school students , consisting of 1055 pages! The book was written by a three-year math teacher at Cambridge, preparing for exams in Cambridge, and his stingy “facts-only” format was very similar to what Ramanujan used in his letter to Hardy.





By the time Ramanujan went to college, he wanted to do only mathematics, and as a result he failed the remaining exams and ran away, so his mother even had to write a letter to the newspaper about the missing person:



Ramanujan moved to Madras (now Chennai ), where he tried to study in different colleges, was ill and as a result continued his independent study in mathematics. In 1909, when he was 21 years old, his mother, in accordance with the customs of that time, arranged his wedding with a 10-year-old girl named Yanaki, who began to live with him a couple of years later.

Ramanujan provided himself with tutoring in mathematics, but he soon became known in the vicinity of Madras as a mathematician and began to publish in the recently launched Journal of the Indian Mathematical Society . His first article , published in 1911, was devoted to the computational properties of Bernoulli numbers (the same Bernoulli numbers that Ada Lovelace (see the article Unraveling the History of Ada Lovelace (First Programmer in History)) on Habré) about the analytical machine). Although his results were not very impressive, Ramanujan’s approach was interesting and original: it combined continuous (“what is the numerical value?”) And discrete (“what is the factorization?”) Mathematics.



After Ramanujan’s mathematician friends fail to get him a scholarship, he begins to look for work, and in March 1912 Ramanujan gets to be an accountant at the port of Madras . His boss - the chief accountant - was interested in academic mathematics and became his lifelong supporter. The head of the port of Madras at that time was an eminent British construction engineer, so Ramanujan, through him, began interacting with some British expatriates. They talked about whether he had “the abilities of a great mathematician” or he was just a “calculator boy”. They wrote to Professor Hill in London, who looked at a number of Ramanujan’s outlandish statements about divergent ranks and said that " Mr. Ramansund is obviously a man with a taste for mathematics, and even with some ability, but he is on the wrong path ." Hill offered Ramanujan to study some books.

While Ramanujan’s friends continued to look for a way to support him, he decided to start writing to British mathematicians himself — even if with some help he could write letters in English. We do not know for sure whom he wrote to the first, although the longtime associate of Hardy, John Littlewood, shortly before his death, 64 years later, mentioned two names: H. F. Baker and E. V. Hobson . Both of them were not a very good choice: Baker worked in the field of algebraic geometry, and Hobson was engaged in mathematical analysis: far enough from what Ramanujan did. In any case, none of them answered.

And on Thursday, January 16, 1913 , Ramanuzhdan wrote his letter to G.Kh. Hardy

Who was hardy?

Godfrey Harold Hardy was born in 1877 into a family of school teachers. They lived about 30 miles south of London . From the very beginning, he was the best student - especially in the field of mathematics. Even when I grew up in England in the early 1970s, such students in high school usually switched to Winchester , and then went to Cambridge . That is what Hardy did. Others were slightly more famous, a little less rigorous and less mathematically oriented — these are Eaton and Oxford (which I entered).

At that time, students of the Cambridge bachelor's program were engaged in solving ornate designed calculus problems (this was reminiscent of serious sporting events), and at the end a rating was made up of students holding positions from “Senior Wrangler” (highest score) to “Wooden Spoon” (the lowest passing score ). Hardy thought he would be the first on the course, but turned out to be the fourth. He concluded that he preferred a strict and formal approach to mathematics, which then became popular in continental Europe.

The British academic system worked at that time (and until the 1960s) in such a way that, after graduating, the best students could be elected college scholarship holders and receive scholarships even for life. Hardy was at Trinity College the largest and scientifically best college at the University of Cambridge, and after graduation in 1900, he was elected a college scholar.

The topic of Hardy's first research paper was integrals like these:



For ten years, Hardy worked mainly on the subtleties of calculation, figured out how to take various types of integrals and their sums, and insisted on a more rigorous approach to the issues of convergence and rearrangement of the limits of integration.

His works were neither great nor visionary, but they became excellent examples of mathematical prowess. Like his colleague Bertrand Russell , he soon began working on a new area - transfinite numbers, but he did not work with them for long. Then in 1908 he wrote the textbook " Pure Mathematics Course " - it was a good and even very successful book (in the preface to it it was said that the textbook was intended for students whose abilities reach the level of "scholarship standard").

By 1910, Hardy plunged into the routine of the life of a professor at the University of Cambridge and was engaged in academic work. And then he met John Littlewood. Littlewood grew up in South Africa and was eight years younger than Hardy, the recent Senior Wrangler and in many ways much more entrepreneurial. And in 1911, Hardy, who previously worked only on his own, joined the collaboration with Littlewood, which lasted the rest of his life.

As a man, Hardy gave the impression of a good schoolboy who never matured. He seemed to enjoy living in a structured environment, concentrating on his mathematical exercises. He was very boring - whether it was about scoring during a cricket game, proof of the absence of God, or writing rules for his collaboration with Littlewood. Being a typical British, he could express himself with intelligence and charm, but he was tough and alienated: he even called himself "G. H. Hardy ", being" Harold "only with his mother and sister.

Thus, by the beginning of 1913, Hardy was a respectable and successful British mathematician interested in a new collaboration with Littlewood, who was drawing him into the field of number theory of interest. But then he received a letter from Ramanujan.

The letter and its consequences

Ramanujan's letter did not start too well: it seemed that he thinks that for the first time he describes a well-known analytical continuation technique for generalizing such ideas and concepts, like factorial , to non-integer numbers . He stated: " I have developed these ideas so much in my research that local mathematicians are not able to understand me and my work ." However, after the cover letter followed more than nine pages, which contained more than 120 different mathematical results.

Initially there were rather vague statements. But on the third page there were formulas for sums and integrals and so on. Some of them vaguely resembled those that were in the works of Hardy. And some of them were definitely more exotic. Their general structure was characteristic of these types of mathematical formulas, but some specific formulas were surprising: they stated that some things were mathematically equal, whereas one could not even expect them to be interconnected.

At least two pages of the original letter were missing. The last page that we have again seems to end badly: Ramanujan, describing the achievements of his theory of divergent series, comes to the seemingly absurd result that the sum of all positive integers is 1 + 2 + 3 + 4 + ... equals -1 / 12.

How did Hardy react? First, he consulted Littlewood. Was this letter a practical joke? Were these formulas already known, or perhaps completely wrong? Some they identified. But the rest - no. Hardy said later that they, too, must be correct, " because if they were not true, no one would have had the imagination to invent them ."

Bertrand Russell wrote that the next day he " found Hardy and Littlewood in a state of wild excitement because they believe they found the second Newton - a Hindu clerk who earns 20 pounds in Madras ." Hardy showed Ramanujan’s letter to many people, and then began making inquiries to government departments governing India. It all took him a week, and then he wrote a response letter to Ramanujan, in which the excitement was clearly read: " I was extremely interested in your letter and the theorems that you formulated ."

He then continued: " However, you must understand that before I can correctly judge the value of what you have done, I must see the evidence of some of your statements ." Curiously, he said it. For Hardy, it was not enough just to know that this was true; he needed proof. Of course, Hardy could have found them on his own. However, it seems to me that in part he wrote this because he wanted to get a more complete picture of how good the mathematician was Ramanujan.

In his letter, with characteristic precision, Hardy divided the contents of Ramanujan’s letter into three categories: what was already known; new and interesting, but not very important; and, finally, new and potentially important. However, the only thing that he attributed to the third category was Ramanujan’s statement on counting prime numbers, adding that “ almost everything depends on the accuracy and rigor of the proof methods you used ”.

Hardy apparently did some preliminary research on the works of Ramanujan by that time, since in his letter he refers to his article on Bernoulli numbers . He writes: " I really hope that you will send me as soon as possible ... some of your evidence, " and then ends with the words: " hoping to get an answer from you as soon as possible ."

Ramanujan really quickly responded to Hardy's letter. First, he wrote that he expected the same answer from Hardy as he did from one " professor of mathematics in London, " who simply told him " not to fall into the trap of divergent rows ." He then responds to Hardy’s strong evidence, saying, “ If I showed you my methods of proof, I’m sure you would have joined the opinion of the London professor .” Then he mentions his result

1 + 2 + 3 + 4 + ... = -1 / 12,

and adds that " ... if I tell you, you will answer that my place is in an insane asylum ." And he continues: " I say this only to convince you that you will not be able to follow my methods of evidence ... based on one letter ." He says that his first goal is to find someone like Hardy to check his results, which means to be able to get a scholarship, since " I already live half hungry. To save brains, I need food ... ".



Ramanujan ends by saying that the presence of the first category of results, which are already known, made him very happy, because " my results are verified - otherwise my position would be too fragile ." In other words, Ramanujan himself was not sure about the results obtained, and he was glad that he was right.

How did he get his results? Later I will talk about this in more detail. But he, of course, did all kinds of calculations with numbers and formulas - in fact, he was engaged in experiments. And, probably, he looked at the results of these calculations in order to understand which of them are correct. It is still unknown how he defined it; In addition, some of his results in the end did not stand up to criticism. Perhaps he used both traditional methods of mathematical proof and confirmation using calculations, and trusted his intuition. However, he did not say any of this to Hardy.

Instead, he simply corresponded with him about the details of the results, and also gave fragments of evidence that he was able to give. It seemed that Hardy and Littlewood intentionally leveled his efforts: for example, Littlewood wrote about some of his results: " (d) - this, of course, is not true ." At the same time, they both wondered whether Ramanujan was “ Euler ” or simply “ Jacobi ”. However, Littlewood said: “the material on primes is incorrect” - in the sense that Ramanujan incorrectly admitted that Zeta - the Riemann function does not have complex zeros, although in reality there are infinitely many of them (Riemann had a whole hypothesis on this subject). Riemann's hypothesis is a well-known and still unsolved mathematical problem that the optimist-teacher suggested Littlewood as a design work when he was still a student.

And what about Ramanujan's strange expression 1 + 2 + 3 + 4 + ... = -1/12? It is also related to the Riemann zeta function. For positive integers, ζ (s) is defined as the sum . In the Wolfram Language there is an interesting function - Zeta [s] - which can be obtained by expanding its domain to the entire set of complex numbers. Then, based on the formula for positive arguments, we can say that Zeta [-1] is the sum of 1 + 2 + 3 + 4 + ... But you can simply calculate Zeta [-1] :



This is too strange a result to simply believe in it. However, not as insane as it may seem at first glance. , ( , , , ).

. . , , , ( , , ). , «» , , « » , - . , , , , « … , , ».

( ) , , , . , , , — , - , - , , , , , . , . , " ; "; " , ".

, , , , . : « XV 3 1904 [ ] . ». , , , .

, , . . , .

— , . . , .





, Mathematica . , . . , .

(, 1970- , , . 9. , — , — «9» «g». , , : " , 9 "!).

, . — , 16, 15.99999. , .

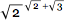- , . , , : or . . , (2,9755 ...) , (3,322 ...). - — , , , — - .

, , , . Mathematica Wolfram Language , .

, , . . , , , .

, , — , , . , , . .

, . . , " ". , . .

. 1970- 1980- . . - , - : «» , . , , , , . — , , . , — , , . , ; .

, , , ( ) , , - . , , . 1910 Orders of Infinity — , ( , ; , , , Wolfram Language).

, « » , , , «» — .

,

- — , . , .

, 1914 " ", ( , ):



: " , , — ; ? " . ( "=" ≅):



, ( ) :



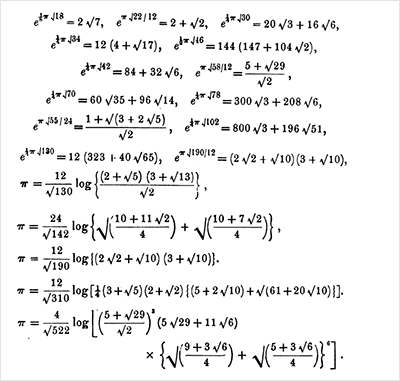
«» ( 1706 ), 239:



: π . 1977 , 35 , . , — , Mathematica Wolfram Language.

, , , ( ) . , :



( ) « »:

Surely for Hardy, Ramanujan’s way of working was alien. Ramanujan was an experimenter in mathematics : he freely entered the universe of mathematical possibilities and did the calculations in order to find interesting and significant facts - and only then built the theories based on them.

Hardy also worked in the traditional vein, gradually expanding the descriptive part of the existing mathematics. Most of his works begin — explicitly or implicitly — with quoting some result from mathematical literature, and then continue with a story about how this result can be spread through a series of precise steps. He has no sudden empirical discoveries, as there are no unexplained jumps based on intuition. His mathematics is thoroughly reasoned and built brick by brick.

A century later, almost all the work in mathematics is done like this. And even if we discuss the same subject, perhaps something should not be called “mathematics,” because the methods are too different. While I was researching the computational universe of simple programs on my own, I did a fair amount of what could be called "mathematical" in the sense that, for example, I researched systems based on numbers .

Over the years I have found all sorts of interesting results. Bizarrely nested recurrence relations that generate prime numbers. Original representations of integers in the form of XOR-trees. But empirical facts alone are not yet part of the tradition of existing mathematics.

For many mathematicians like Hardy, the proof process is the basis of mathematical activity. It is easy to make an assumption that is true; more important is to create evidence that explains why something is true, so that other mathematicians understand this.

Today, when we have the opportunity to automate more and more evidence, this process begins to resemble manual labor, where the result may be interesting, and the process of obtaining it will not. But the process of proof can also be important. Evidence can be the material by which new abstract concepts are introduced that go beyond the details of this evidence, and also provide “raw material” for understanding many other mathematical results.

I suspect that Ramanujan, for whom these facts and results were the center of his mathematical thinking, felt like a strange European customs, necessary to take his results from their specific context and to convince European mathematicians that they were true.

Going to Cambridge

But back to the story of Ramanujan and Hardy.

By early 1913, Hardy and Ramanujan continued to exchange letters. Ramanujan described his results; Hardy criticized him and insisted on evidence and their traditional presentation. Then there was a long break, but in December 1913, Hardy wrote again, saying that Ramanujan’s most ambitious results on the distribution of prime numbers were definitely incorrect, adding that " ... the theory of prime numbers is full of pitfalls, overcoming of which requires the use of modern rigorous methods ." He also said that if Ramanujan could prove his results, it would be " one of the most remarkable mathematical achievements in the entire history of mathematics ."

In January 1914, a young Cambridge mathematician E.H. Neville came to Madras to lecture and reported that Hardy "was seeking to transfer Ramanujan to Cambridge." Ramanujan answered that back in February 1913, he and his boss had a meeting with the secretary of the advisory student committee of Madras, who asked if he was ready to go to England. Ramanujan wrote that he assumed that he would have to pass exams in the same way as other Indian students who were leaving for England (and he thought he could not cope with this), and also that his boss was a " very orthodox Brahmin, and since he doubted whether to go to a foreign land, he told me that it was not worth it . "

He later told that Neville “dispelled [his] doubts,” explaining that he didn’t have to worry about expenses, that he was happy with his English, that he didn’t have to pass exams, and that he could remain a vegetarian in England. Ramanujan ended by saying that he hoped that Hardy and Littlewood would be " kind enough to take the trouble of accepting me [in England] for several months ."

Hardy suggested that there would be no bureaucratic problems and Ramanujan would easily fall into England; However, it did not happen that way. Trinity College, where Hardy worked, was not prepared to provide any real funding. Hardy and Littlewood offered their money, but Neville wrote to the secretary of the University of Madras : "The discovery of genius S. Ramanujan from Madras promises to be the most interesting event of our time in the mathematical world ," he suggested that the university find the money. Ramanujan’s expatriates took active steps, ultimately won the attention of the Governor Madras, and found the money: they were taken from a government grant five years ago, meant for “establishing lectures at the university during the holidays”, and in the language of bureaucracy it sounded like this: “ Document No. 182 of the Department of Education "..." not used for its intended purpose.

The bureaucratic protocols were strange registry - for example, on February 12: “To which caste does he belong? Urgently. But in the end, all difficulties were overcome, and on March 17, 1914, after seeing off wires with the participation of local dignitaries, Ramanujan boarded a ship to England, going up the Suez Canal , and arriving in London on April 14 . Before leaving India, Ramanujan was preparing for European life: he wore Western clothes, learned to eat with a knife and fork and tie a tie. For those Indian students who came to England before, there was a whole procedure. A few days later, Ramanujan arrived in Cambridge, and Indian newspapers proudly reported that " Mr. S. Ramanujan of Madras, whose advanced mathematics work caused surprise at Cambridge, is currently in residence in Trinity ."

(In connection with the first days of Ramanujan, in Cambridge, in addition to the names Hardy and Littlewood, two other names appear: Neville and Barnes . They are not particularly known in the general history of mathematics, but it so happens that in Wolfram Language their names have built-in functions: NevilleThetaS and BarnesG ) .

Ramanujan at Cambridge

What was Ramanujan like when he arrived in Cambridge? He is described as full of enthusiasm and an active person, albeit unsure of himself. He was joking, sometimes in his address. He could speak not only about mathematics, but also about politics and philosophy. He was not too reflexive. When communication was official, he was polite and respectful and tried to follow local customs. His native language was Tamil , and he had previously failed, failing the English exams, but by the time he arrived in England, his English was excellent. He loved hanging out with other Indian students, sometimes going to music events or boating on the river. He was short and full; His main remarkable feature was his bright and brilliant eyes. He worked hard solving one math problem after another. His meager living space comprised only a few books and articles. He was prudent in practical things: for example, to solve problems with cooking and finding vegetarian foods. We can say that in Cambridge he was happy.

However, later, on June 28, 1914 (just two and a half months after Ramanujan arrived in England), the Archduke Ferdinand was killed, and World War I began on July 28. This immediately affected Cambridge. Many students were called up for military service. Littlewood joined the military and eventually developed a method for calculating range tables for anti-aircraft guns. Hardy was not a big supporter of the war (not least because he loved German mathematicians), but he also volunteered and was subsequently rejected for medical reasons.

Ramanujan described the war in letters to his mother, saying, for example: “ they fly in airplanes at high altitude, bomb cities and destroy them. As soon as enemy aircraft appear in the sky, airplanes standing on the ground take off and at great speed that brings destruction and death . "

Ramanujan nevertheless continued his studies in mathematics, explaining to his mother that "the war is fought in territories as remote as Rangoon is far from [Madras] ." There were practical difficulties, for example, the lack of vegetables, which prompted Ramanujan to ask a friend from India to send him a packet of " some tamarind seeds and good coconut oil ." More importantly, as Ramanujan wrote, " professors here ... lost interest in mathematics because of the current war ."

Ramanujan also wrote to a friend that "he changed the plan for publishing his results ." He said he would wait for the end of the war in order to publish any of his old results. But he said that from the moment of his arrival in England he had mastered " their methods ", and he is trying to " get new results by their methods so that it can be published easily and without delay ."

In 1915, Ramanujan published a long document entitled " high-grade numbers " about function maxima ( DivisorSigma in the Wolfram Language), which counts the number of divisors of a given number. Hardy, in all likelihood, took an active part in the preparation of this article, which became the basis of theses for Ramanujan’s master’s thesis.

Over the next few years, Ramanujan worked fruitfully and wrote articles that, despite the war, were published. Together with Hardy, he wrote a significant article on the distribution function ( PartitionsP in Wolfram Language), describing ways to write an integer as the sum of positive numbers. This article is a classic example of mixing approximate and exact calculations. The article begins with a result for large n :



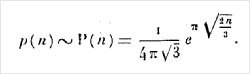
But then with the help of the ideas of Ramanujan, developed in India, the estimate is gradually improved to the point where the resulting integer can be obtained. At the time in which Ramanujan lived, the calculation of the exact value of PartitionsP [200] was a big deal - and the culmination of his article. But today, thanks to the Ramanujam method, these calculations can be carried out instantly:



Cambridge was crushed by the war - on the front lines the students died at a terrifying speed. The large quadrilateral of Trinity College has become a military hospital. But despite all this, Ramanujan continued to study mathematics - and with the help of Hardy earned himself fame.

In May 1917, Ramanujan fell ill. As far as can now be judged, it was probably some kind of parasitic liver infection brought from India. But then no one could diagnose. Ramanujan went from doctor to doctor, but he did not believe what he was told, and it seemed that nothing would help. In one months, he felt well enough to study mathematics; to others not. He fell into depression, and at some point, apparently, was prone to suicide. He was not helped by the fact that his mother brought his wife back to India, protecting him from communicating with her and fearing that she would distract him.

Hardy tried to help: sometimes - interacting with doctors, sometimes - providing mathematical data. One doctor told Hardy that the cause of the disease could be " some unknown pathogen from the East, completely unexplored at the present time ." Hardy wrote: " Like all Indians, Ramanujan is a fatalist, and therefore terribly difficult to make him take care of himself ." Later, Hardy told the famous story about how he once visited Ramanujan in the hospital and said that he came by taxi with number 1729, and that it seems to him that this is a rather dull number, to which Ramanujan replied: " No, this is a very interesting number ; this is the smallest number that can be represented as the sum of two cubes in two different ways ": . (Wolfram | Alpha now also reports on some of its other properties ).

However, despite all the problems, Ramanujan’s reputation as a mathematician continued to grow. He was elected a member of the Royal Society (which included Hobson and Baker, none of whom responded to his original letter), and in October 1918 he was elected a member of Trinity College, which provided him with financial support. A month after the end of the First World War, the threat of a submarine attack, which made the journey to India dangerous, disappeared.

And on March 13, 1919, Ramanujan returned to India - very famous and respected and very sick. He is still engaged in mathematics and, in particular, Hardy writes a conspicuous letter about "false" theta functions ( January 12, 1920 ). He decided to live modestly, and largely ignored the little that medicine could do for him. And on April 26, 1920, at the age of 32 and three days after the last entry in the notebook, he dies.

What happened next

When Ramanujan began to do research in mathematics, he wrote down his results in notebooks with a hard cover , publishing only a small part of them. When Ramanujan died, Hardy wanted to study and publish all 3,000 (or so) results from Ramanujan's notebooks. Several people also worked on this in the 1920s and 1930s, and in the end a lot of things were published. However, the project was not completed - it will be returned only in the 1970s.





Download the first , second , third notebook.

In 1940, Hardy handed all the letters he had to Ramanujan to the library of the University of Cambridge , but the original letter that Ramanujan sent in 1913 was not among them, so now the only thing we have is a later transcription of this letter from Hardy . For three years, Ramanujan’s three major notebooks lay on a cabinet in the office of a librarian at the University of Madras, where they suffered from insects, but were not lost. His other records went through several hands, and some of them ended up in the incredibly dirty office of the Cambridge mathematician ; however, when he died in 1965, they were noticed and sent to the library, where they were gathering dust until they were “rediscovered” in 1976 as Ramanujan's lost records .

When Ramanujan died, his relatives almost immediately began to ask for financial support. Great bills for treatment came from England, and talk began of selling Ramanujan papers to collect money.

Ramanujana’s wife was 21 when he died, but she no longer married. She lived very modestly, earning her living by sewing. In 1950, she took on the upbringing of the son of a deceased friend. By the 1960s. Ramanujan became something like an Indian hero, and she began to receive various awards and pensions. Over the years, many mathematicians came to visit her, one of whom she gave a photograph from Ramanujan's passport, which became his most famous image.

She lived a long life and died in 1994 at the age of 95 years, having survived Ramanujan by 73 years.

What happened to Hardy?

Hardy was 35 years old when he received a letter from Ramanujan, and 43 years old when he died. Hardy regarded Ramanujan’s “discovery” as his greatest achievement, and described their collaboration as the “ first romantic event of his life .” After the death of Ramanujan, Hardy worked for some time, continuing to decode and develop his results, but for the most part he returned to his former mathematical trajectory. The complete collection of his works consists of seven large volumes (whereas the publications of Ramanujan - one thin little book). These clouds from the names of his works show only some of the changes that have occurred (the first cloud - before the meeting with Ramanujan, the second - after):



Shortly before Ramanujan entered his life, Hardy began working with John Littlewood (he would say later that Littlewood had an even greater influence on his life than Ramanujan). After Ramanujan died, Hardy moved to Oxford for work and lived there for 11 years before returning to Cambridge. His absence did not affect cooperation with Littlewood, as they worked mainly through the exchange of written messages, even if their rooms were only a few hundred feet from each other. After 1911, Hardy published without a co-author; most productively, he worked with Littlewood, having published 95 articles in 38 years with his co-authorship.

Math Hardy has always been of the highest quality. He dreamed of creating something like a solution to the Riemann hypothesis, but in reality he did not do anything really exciting. He wrote two books that still read to this day: “An Introduction to Number Theory” with EM. Wright ; and "Inequality" together with Littlewood and D. Poya .

Hardy lived his life among the intellectual elite. In the 1920s, he hung the image of Lenin in his apartment and was briefly the president of the “science workers” trade union. : , . . , ( , ).

1940 . 12, . , . , . , — , , — , , " , - , " ( , - , ). , , .



, , , . , , " … ". , " 30 , , ". , , 1970- , — .



Is it really? I doubt it. , ( Wolfram|Alpha Wolfram Language) , . ( 40, , , ), , , 30 .



, . , , . , , . , . , , , . , , — . , , , , . , . , , , , .

, ( ) , , , , .

. , , , . 1947 70 .

, , 1977 . , , . , , , - , . , 72 , 80, , — .

? — . - , , , . , , « », ( Zentralblatt ):



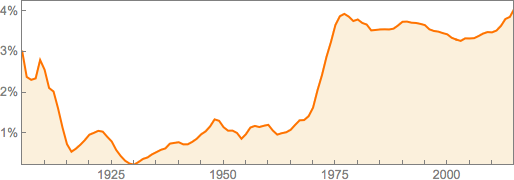
1900- . (, , ). 1930- . , .

1970- , ( , , , ).

1970- , , , , , . 1982 , , ( , - ):



1970- ( , ), . , .

- . (-, , - ..) «». ; , «», , .

, , Mathematica Wolfram Language , RamanujanTau , RamanujanTauL , RamanujanTauTheta RamanujanTauZ . , . , « -» ( , ).

- , ( «24»):



, — , - , .

— ?

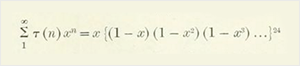
, 1 + 2 + 3 + 4 = 10. , , . , . ( ) , . — , .

, , , . , . . , , , , . , , — .

. , , , .

? , . -, , , , , , . , , , , , .

, ; , . , . . . , , , - . 1931 ( , , -, ) , -: , .

1960- . , , ( ) , . . , , , , . , , , . , , , (, ).

, , . . .

, , , . , ; , .

, , , «» , .

, , . , , , - . , .

, , . , , , , .

, , . : ?

, . , . , , . , « ». .

, , . , , , ( - ) «» .

, . , , : . , . ( ), .

, , , ? , . , , , - .

, « »: , , . — . : .

, , , . , . , — , .

?

- ? , , , , 30 , — , 1913 . , , ( ) , , .



? … Wolfram|Alpha , , .



. , . AI . , , : - , , . ; . ( ) - , «», .

, «» , . , . , ( ), . , , .

, , , . . - , . , , , , , .

. , , , . , . , , , — , , .

« »: , , , . , , Mathematica Wolfram Language . , : , , . , , .

, : . , , , , , - ( ) .

, , ( ).

, - , . , . , , , (, , ), . - Wolfram Language . , - , , .

, . (. " Wolfram: " ) - . ( ) , . , — . , - 14- , , , …

, Mathematica?

— , — . (Mathematica Wolfram Language), ( ).

, . , , , , , , .

. , , , : , .

, , . — , . , , , — .