Optimization of image processing using GPU on the example of Median filtering
Introduction
Long since graphic accelerators (GPU) were created for image processing and video. At some point, the GPU began to be used for general purpose calculations. But the development of central processors did not stand still either: Intel was actively developing the development of vector extensions (AVX256, AVX512, AVX1024). As a result, different processors appear - Core, Xeon, Xeon Phi. Image processing can be attributed to this class of algorithms that are easily vectorized.
But as practice shows, despite the rather high level of compilers and manufacturability of Xeon Phi central processors and co-processors, it is not so easy to make image processing using vector instructions, as modern compilers do not cope with automatic vectorization, and using vector intrinsic functions is rather laborious. It also raises the question of combining vectorized code and scalar sections.
This article has discussed how to use vector extensions to optimize median filtering for CPUs. For the purity of the experiment, I took all the same conditions as the author: I used the median filtering algorithm using a 3x3 square, these images take 8 bits per pixel, the processing of the frame (depending on the size of the filtering square) is not done; and tried to optimize this core on the GPU. The algorithm of the median filtering of squares 5x5 was also considered. The essence of the algorithm is as follows:
- For each point of the original image, a certain neighborhood is taken (in our case, 3x3 / 5x5).
- The points of this neighborhood are sorted by increasing brightness.
- The average point of the sorted neighborhood is written to the final image.
The first implementation of the kernel on the GPU
In order not to engage in "extra" optimization, we will use some calculations of the author of the article mentioned. And in the end you get simple code computational core
__device__ __inline__ void Sort(int &a, int &b) { const int d = a - b; const int m = ~(d >> 8); b += d & m; a -= d & m; } __global__ void mFilter(const int H, const int W, const unsigned char *in, unsigned char *out) { int idx = threadIdx.x + blockIdx.x * blockDim.x + 1; int idy = threadIdx.y + blockIdx.y * blockDim.y + 1; int a[9] = {}; if (idy < H - 1 && idx < W - 1) { for (int z2 = 0; z2 < 3; ++z2) for (int z1 = 0; z1 < 3; ++z1) a[3 * z2 + z1] = in[(idy - 1 + z2) * W + idx - 1 + z1]; Sort(a[1], a[2]); Sort(a[4], a[5]); Sort(a[7], a[8]); Sort(a[0], a[1]); Sort(a[3], a[4]); Sort(a[6], a[7]); Sort(a[1], a[2]); Sort(a[4], a[5]); Sort(a[7], a[8]); Sort(a[0], a[3]); Sort(a[5], a[8]); Sort(a[4], a[7]); Sort(a[3], a[6]); Sort(a[1], a[4]); Sort(a[2], a[5]); Sort(a[4], a[7]); Sort(a[4], a[2]); Sort(a[6], a[4]); Sort(a[4], a[2]); out[idy * W + idx] = (unsigned char)a[4]; } } For each point, the neighborhood is loaded according to the given picture (the pixel of the image for which you want to calculate the result is highlighted in yellow):
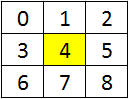
In this implementation, there is one drawback - the image is stored in an 8-bit format, and calculations take place in a 32-bit one. If you look into the combat code of the vector implementation on the CPU, you can see that there have been many optimizations, including eliminating unnecessary operations during sorting, since depending on the compiler, optimization may not work. The Nvidia compiler lacks such flaws - it can easily deploy two cycles on z2 and z1 even if no #pragma unroll is specified (in this case, the compiler will decide whether to roll the loop itself, and if there are not enough registers, then the cycles will not be deployed) as well as unnecessary operations of the Sort functions after their substitution will be excluded (the inline directive is advisory, if you need to substitute the function, regardless of how the compiler decides, you must use forceinline ).
I will test on the Nvidia GTX 780 Ti GPU of approximately the same year of production as the central processor in the article above (Intel Core-i7 4770 3.4 GHz). Image size is 1920 x 1080 black and white. If we run the compiled first version on the GPU, we get the following times:
| Runtime, ms | Relative acceleration | ||||
|---|---|---|---|---|---|
| Scalar CPU | AVX2 CPU | Version1 GPU | Scalar / AVX2 | Scalar / Version1 | AVX2 / Version1 |
| 24.814 | 0.424 | 0.372 | 58.5 | 66.7 | 1.13 |
As can be seen from the above times, simply rewriting the code "natively" and running it on the GPU, we get quite a good acceleration, and there are no problems with aligning the image size - the code on the GPU will work equally well on any image size (respectively, starting from some size when the GPU is fully loaded). You also don’t have to think about memory alignment - the compiler will do everything for us; it’s enough to allocate memory using special CUDA RunTime functions.
Many who are faced with graphics accelerators, will immediately say that you need to download data and unload it back. With a PCIe 3.0 speed of 15 GB / s, for a 2 MB image, about 130 microseconds are obtained for one-way transfer. Thus, if stream processing of images takes place, the download + upload will take about 260 microseconds, while the counting takes about 372 microseconds, which means that even in the most "native" implementation, transmissions to the GPU are covered. You can also conclude that faster than 260 microseconds per image, you cannot handle the stream of images. But if this filter is used together with another dozen of filters during the processing of one image, then further optimization of this kernel becomes useful.
The second implementation of the kernel on the GPU
In order to increase the efficiency of sorting operations, you can use newly added SIMD instructions. These instructions are intrinsics functions that allow you to compute a certain mathematical function for two unsigned / signed short or for 4 unsigned / signed char in one operation. A list of available functions can be found in the Cuda ToolKit documentation . We need two functions: vminu4 (unsigned a, usnigned b) and vmaxu4 (unsigned a, unsigned b); calculating the minimum and maximum for 4 without the sign 8-bit values. To load four values, we divide the entire image into 4 parts horizontally and each block will load data from 4 bands, combining 4 loaded points using a bit-wise shift into an unsigned int:
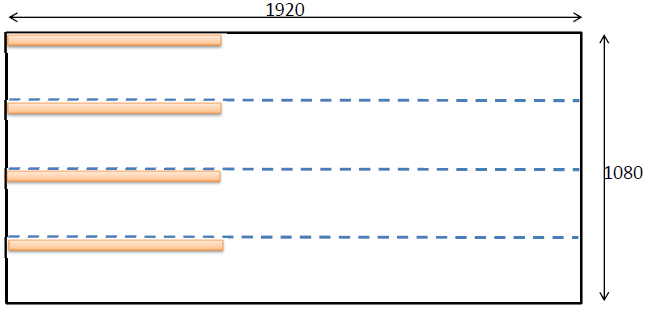
The active processing area is the uppermost square with a size of 1920 x 270. Accordingly, a block of 128 x 1 threads is shown in orange, which will load 128 * 4 elements. As is known, the size of the warp on the GPU consists of 32x threads. All threads of one warp perform one instruction per clock at a time. Since each thread will load to itself 4 unsigned char elements, one warp in total will process 128 elements per instruction, that is, some 1024 bit processing is obtained. For the CPU, 256 bit AVX2 registers are currently available (which will turn into 512 and 1024 bit in the future). With these optimizations, the computational kernel code is converted to the following form:
__device__ __inline__ void Sort(unsigned int &a, unsigned int &b) { unsigned t = a; a = __vminu4(t, b); b = __vmaxu4(t, b); } __global__ __launch_bounds__(256, 8) void mFilter_3(const int H, const int W, const unsigned char * __restrict in, unsigned char *out, const unsigned stride_Y) { int idx = threadIdx.x + blockIdx.x * blockDim.x + 1; int idy = threadIdx.y + blockIdx.y * blockDim.y + 1; unsigned a[9] = { 0, 0, 0, 0, 0, 0, 0, 0, 0 }; if (idx < W - 1) { for (int z3 = 0; z3 < 4; ++z3) { if (idy < H - 1) { const int shift = 8 * (3 - z3); for (int z2 = 0; z2 < 3; ++z2) for (int z1 = 0; z1 < 3; ++z1) a[3 * z2 + z1] |= in[(idy - 1 + z2) * W + idx - 1 + z1] << shift; } idy += stride_Y; } Sort(a[1], a[2]); Sort(a[4], a[5]); Sort(a[7], a[8]); Sort(a[0], a[1]); Sort(a[3], a[4]); Sort(a[6], a[7]); Sort(a[1], a[2]); Sort(a[4], a[5]); Sort(a[7], a[8]); Sort(a[0], a[3]); Sort(a[5], a[8]); Sort(a[4], a[7]); Sort(a[3], a[6]); Sort(a[1], a[4]); Sort(a[2], a[5]); Sort(a[4], a[7]); Sort(a[4], a[2]); Sort(a[6], a[4]); Sort(a[4], a[2]); idy = threadIdx.y + blockIdx.y * blockDim.y + 1; for (int z = 0; z < 4; ++z) { if (idy < H - 1) out[idy * W + idx] = (unsigned char)((a[4] >> (8 * (3 - z))) & 255); idy += stride_Y; } } } As a result of small changes, we increased the number of processed elements to 4x (or 128 elements per instruction). The complexity of the code has increased and the compiler generates too many registers, which makes it impossible to load the hcp by 100%. Since we still have simple calculations, we will tell the compiler that we want to run the maximum possible number of threads on each stream processor (maximum for a given GPU is 2048 threads) using __launch_bounds (128, 16), which means that A configuration of 16 blocks of 128 threads each was launched. And one more innovation - we will add the restrict keyword to use the texture cache to load duplicate data (if analyzed, there are quite a few of them, most of the points are read 3 times). In order for the texture cache to be enabled, you also need to specify const. All together, the instruction will look like this:
const unsigned char * __restrict in. Corresponding times of the second version:
| Runtime, ms | Relative acceleration | ||||||
|---|---|---|---|---|---|---|---|
| Scalar CPU | AVX2 CPU | Version1 GPU | Version2 GPU | Scalar / AVX2 | Scalar / Version2 | AVX2 / Version2 | Version1 / Version2 |
| 24.814 | 0.424 | 0.372 | 0.207 | 58.5 | 119.8 | 2.04 | 1.79 |
Third kernel implementation on the GPU
Already received not a bad acceleration. But you can see that loading 4 elements with such a distance causes too many repeated downloads. This significantly reduces speed. Is it possible to somehow use what we have already loaded directly on the registers and improve the locality of the data? Yes you can! Let these 4 lines are now located close to each other, and the beginning of the blocks will be "smeared" along the entire height with a distance of 4. Thus, taking into account the block size of the threads in Y, we arrive at the following code:
#define BL_X 128 #define BL_Y 1 __device__ __inline__ void Sort(unsigned int &a, unsigned int &b) { unsigned t = a; a = __vminu4(t, b); b = __vmaxu4(t, b); } __global__ __launch_bounds__(256, 8) void mFilter_3a(const int H, const int W, const unsigned char * __restrict in, unsigned char *out) { int idx = threadIdx.x + blockIdx.x * blockDim.x + 1; int idy = threadIdx.y + blockIdx.y * blockDim.y * 4 + 1; unsigned a[9] = { 0, 0, 0, 0, 0, 0, 0, 0, 0 }; if (idx < W - 1) { for (int z3 = 0; z3 < 4; ++z3) { //if (idy < H - 1) <---- this is barrier for compiler optimization { const int shift = 8 * (3 - z3); for (int z2 = 0; z2 < 3; ++z2) for (int z1 = 0; z1 < 3; ++z1) a[3 * z2 + z1] |= in[(idy - 1 + z2) * W + idx - 1 + z1] << shift; } idy += BL_Y; } Sort(a[1], a[2]); Sort(a[4], a[5]); Sort(a[7], a[8]); Sort(a[0], a[1]); Sort(a[3], a[4]); Sort(a[6], a[7]); Sort(a[1], a[2]); Sort(a[4], a[5]); Sort(a[7], a[8]); Sort(a[0], a[3]); Sort(a[5], a[8]); Sort(a[4], a[7]); Sort(a[3], a[6]); Sort(a[1], a[4]); Sort(a[2], a[5]); Sort(a[4], a[7]); Sort(a[4], a[2]); Sort(a[6], a[4]); Sort(a[4], a[2]); idy = threadIdx.y + blockIdx.y * blockDim.y * 4 + 1; for (int z = 0; z < 4; ++z) { if (idy < H - 1) out[idy * W + idx] = (unsigned char)((a[4] >> (8 * (3 - z))) & 255); idy += BL_Y; } } } Optimized code in this way allows the compiler to use already loaded data. The only problem is the condition check (idy <H - 1). In order to remove this check, you need to add the required number of lines, that is, align the image vertically by 4, and fill in all the additional elements with the maximum number (255). After converting the code to the third option, the times will be as follows:
| Runtime, ms | Relative acceleration | ||||||
|---|---|---|---|---|---|---|---|
| Scalar CPU | AVX2 CPU | Version1 GPU | Version2 GPU | Version2 GPU | Scalar / AVX2 | Scalar / Version3 | AVX2 / Version3 |
| 24.814 | 0.424 | 0.372 | 0.207 | 0.130 | 58.5 | 190.8 | 3.26 |
Further, it is already quite difficult to optimize, since there are not so many calculations here. The issue of shared memory has not been raised here. There were some attempts to use shared memory, but the best time I could not get. If you link the processing speed of the image with its size, then regardless of whether the picture is aligned in size or not, you can get about 15 GigaPixels / second.
The core of the median filter 5x5 on the GPU
By applying all the optimizations, you can implement a 5x5 square filter with minor changes. The complexity of this code is the correct implementation of partial bitonic sorting for 25 elements. By analogy, you can implement filters of any size (starting with some filter size, there will surely be a quick general sorting algorithm).
__global__ __launch_bounds__(256, 8) void mFilter5a(const int H, const int W, const unsigned char * in, unsigned char *out, const unsigned stride_Y) { int idx = threadIdx.x + blockIdx.x * blockDim.x + 2; int idy = 4 * threadIdx.y + blockIdx.y * blockDim.y * 4 + 2; if (idx < W - 2) { unsigned a[25] = { 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 }; for (int t = 0; t < 4; ++t) { const int shift = 8 * (3 - t); for (int q = 0; q < 5; ++q) for (int z = 0; z < 5; ++z) a[q * 5 + z] |= (in[(idy - 2 + q) * W + idx - 2 + z] << shift); idy++; } Sort(a[0], a[1]); Sort(a[3], a[4]); Sort(a[2], a[4]); Sort(a[2], a[3]); Sort(a[6], a[7]); Sort(a[5], a[7]); Sort(a[5], a[6]); Sort(a[9], a[10]); Sort(a[8], a[10]); Sort(a[8], a[9]); Sort(a[12], a[13]); Sort(a[11], a[13]); Sort(a[11], a[12]); Sort(a[15], a[16]); Sort(a[14], a[16]); Sort(a[14], a[15]); Sort(a[18], a[19]); Sort(a[17], a[19]); Sort(a[17], a[18]); Sort(a[21], a[22]); Sort(a[20], a[22]); Sort(a[20], a[21]); Sort(a[23], a[24]); Sort(a[2], a[5]); Sort(a[3], a[6]); Sort(a[0], a[6]); Sort(a[0], a[3]); Sort(a[4], a[7]); Sort(a[1], a[7]); Sort(a[1], a[4]); Sort(a[11], a[14]); Sort(a[8], a[14]); Sort(a[8], a[11]); Sort(a[12], a[15]); Sort(a[9], a[15]); Sort(a[9], a[12]); Sort(a[13], a[16]); Sort(a[10], a[16]); Sort(a[10], a[13]); Sort(a[20], a[23]); Sort(a[17], a[23]); Sort(a[17], a[20]); Sort(a[21], a[24]); Sort(a[18], a[24]); Sort(a[18], a[21]); Sort(a[19], a[22]); Sort(a[9], a[18]); Sort(a[0], a[18]); Sort(a[8], a[17]); Sort(a[0], a[9]); Sort(a[10], a[19]); Sort(a[1], a[19]); Sort(a[1], a[10]); Sort(a[11], a[20]); Sort(a[2], a[20]); Sort(a[12], a[21]); Sort(a[2], a[11]); Sort(a[3], a[21]); Sort(a[3], a[12]); Sort(a[13], a[22]); Sort(a[4], a[22]); Sort(a[4], a[13]); Sort(a[14], a[23]); Sort(a[5], a[23]); Sort(a[5], a[14]); Sort(a[15], a[24]); Sort(a[6], a[24]); Sort(a[6], a[15]); Sort(a[7], a[16]); Sort(a[7], a[19]); Sort(a[13], a[21]); Sort(a[15], a[23]); Sort(a[7], a[13]); Sort(a[7], a[15]); Sort(a[1], a[9]); Sort(a[3], a[11]); Sort(a[5], a[17]); Sort(a[11], a[17]); Sort(a[9], a[17]); Sort(a[4], a[10]); Sort(a[6], a[12]); Sort(a[7], a[14]); Sort(a[4], a[6]); Sort(a[4], a[7]); Sort(a[12], a[14]); Sort(a[10], a[14]); Sort(a[6], a[7]); Sort(a[10], a[12]); Sort(a[6], a[10]); Sort(a[6], a[17]); Sort(a[12], a[17]); Sort(a[7], a[17]); Sort(a[7], a[10]); Sort(a[12], a[18]); Sort(a[7], a[12]); Sort(a[10], a[18]); Sort(a[12], a[20]); Sort(a[10], a[20]); Sort(a[10], a[12]); idy = 4 * threadIdx.y + blockIdx.y * blockDim.y * 4 + 2; for (int z = 0; z < 4; ++z) { if (idy < H - 2) out[idy * W + idx] = (unsigned char)((a[12] >> (8 * (3 - z))) & 255); idy++; } } } The processing speed of the filter of this size will be about 5.7 times faster when using the AVX2, while the GPU version will slow down just 3.8 times (about 0.5 ms). The final acceleration on the GPU with a median filtering square 5x5 can reach 5 times compared with the AVX2 version.
Conclusion
In conclusion, you can sum up some of the results. By optimizing a sequential scalar program, you can get great accelerations using a graphics processor. For median filters, depending on the filtering radius, the acceleration values can reach 1000 times! Of course, a very optimal version using AVX2 instructions dramatically reduces the gap between the GPU and the CPU. But personally, from my own experience, I can conclude that vectorizing code manually is not as easy as it actually seems. On the contrary, even the most "native" implementation on the GPU gives quite high accelerations. And in most cases it is enough. And if we consider that the number of graphics cards in one motherboard may be more than one, the overall acceleration of processing images or video may increase linearly.
The question of whether to use the GPU or not, is rhetorical. Of course, in tasks of image processing and video, the GPU will show better performance and with increasing computational load, the difference between the processing speed of the CPU and the GPU will increase in favor of the latter.
Combat optimizations are available in the second article: Faster, faster or in-depth optimization of Median filtering for Nvidia GPUs.
')
Source: https://habr.com/ru/post/305964/
All Articles